logo资料库

从PID技术到_自抗扰控制_技术.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.32M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    ¾ 2002 年 5 月 第9 卷第3 期 控 制 工 程 Control Engineering of China May 2 0 0 2 Vol. 9 ,No . 3 文章编号 : 1005 3662 (2002) 03 0013 06 从 PID 技术到“自抗扰控制”技术 (中国科学院 数学与系统科学研究院 系统科学所 , 北京 　100080) 韩 京 清 摘 　　　要 : 从传统 PID 的原理出发 ,分析了它的优缺点。利用非线性机制来开发了一些具有特殊功能的环 节 :跟踪微分器 ( TD) ,扩张状态观测器 ( ESO) ,非线性 PID (NPID) 等 ,并以此组合出高品质的新型控制器 - 自抗 扰控制器 (ADRC) ,从而形成了新的“自抗扰控制”技术。新型的控制器具有算法简单、参数易于调节的特点。 关 　键 　词 : PID ;非线性反馈 ;自抗扰控制 中图分类号 : TP 13 　　　文献标识码 : A 1 　引 　言 PID 控制器在工业过程控制中占据的主导地 位是绝无仅有的 。目前 ,PID 控制器在运动控制 、 航天控制及其他过程控制的应用中 ,仍然占据 95 %以上 。据最新的文献 1 显示 ,在纸浆和造纸工 业中 ,PI 控制器的应用甚至超过了 98 %。由此 可见 ,不管现代控制理论给出的控制方法在理论 上是多么的完美而漂亮 ,可是仍然难以在现代的 工业控制中找到自己的立足之处 。这说明时至今 日 ,控制理论和工程实际相脱离的鸿沟不但没有 弥合的迹象 ,反而有了加剧的趋势 。 面对这种尴尬的局面 ,我们不得不重新认识 PID 控制技术 ,探索其机理 ,发扬其优势 ,克服其 缺点 ,进而寻找更好的控制技术 。本文的出发点 就在于此 。 2 　传统 PID 的结构及优 、缺点 传统 PID 的结构如图 1 所示 。 和变化趋势的加权和控制策略 。PID 在实际中大 量应用 ,但不易满足高性能要求 ,于是想靠对象模 型来寻求更好的控制方法 ,但靠模型的路子恰恰 把 PID 的最大优点丢掉了 。 PID 的优点 :靠控制目标与实际行为之间的 误差来确定消除此误差的控制策略 。 PID 的缺点 : ①误差的取法 ; ②由误差 e 提取 d e/ d t 的办法 ; ③“加权和”策略不一定最好 ; ④积 分反馈有许多副作用 。 我们的思路是探讨更好的控制策略 ,这种策 略的宗旨是保留 PID 的优点 ,克服其缺点 。我们 的工具是利用特殊非线性效应来开发具有特殊功 能的环节 ,并以此来组合出高品质控制器 。 克服 PID“缺点”的具体办法是 : ①安排合适 的“过渡过程”; ②合理提取“微分” “跟踪微分器” ( Tracking Differentiator , TD) ; ③探讨合适的组合 方法 “非线性组合”(N F) ; ④探讨“扰动估计”办 法 “扩张状态观测器”( Extended State Observer , ESO) 。 下面 ,我们以二阶对象控制为例来讨论保留 PID 的优点 ,克服其缺点的办法 。 3 　合理提取微分的方法 “跟踪微分器” 图 1 　传统 PID 的结构 ( TD) u = k0∫t 0 edτ + k1 e + k2 d e d t 工业过程控制的 PID 控制原理是基于误差 来生成消除误差的控制策略 :用误差的过去 、现在 1) 经典微分器的形式为 : 1 τ 1 - τs + 1 v = y = w ( s) v = s 1 τs + 1 v , y ( t) ≈ 1 τ( v ( t) - v ( t - τ) ) ≈ v ( t) 收稿日期 : 2002 - 04 - 08 作者简介 : 韩京清 (1937 - ) ,男 (朝鲜族) ,吉林长白人 ,研究员 ,大学本科 ,主要从事控制理论与应用等方面的教学与科研工作。
    ¾ ¾ ·41· 控 　制 　工 　程 　　　　　　 　　　　　　　　第 9 卷 τ2 - τ1 1 式中 , v ( t) , y ( t ) 分别是系统的输入 、输出信号 , w ( s) 是系统的传递函数 。当对信号 v ( t) 叠加随 机噪声 n ( t) 时 y ( t) ≈ 1 τ( v ( t) - v ( t - τ) ) + n ( t) τ ≈ v ( t) + 1 τn ( t) τ越小时 ,系统输出的“噪声放大”就越严重 。 若用近似微分公式 v ( t) ≈ v ( t - τ2) - v ( t - τ1) ,0 < τ1 < τ2 , 则有 y = 1 τ2 - τ1 τ1 s + 1 - 1 τ2 s + 1 v = s τ1τ2 s2 + (τ1 +τ2) s + 1 v 可以降低“噪声放大”的效应 。 这里 ,“微分”信号是用“尽快地跟踪输入信 号”的办法得到的 。那么能否用“最快地跟踪”的 办法得到微分信号呢 ? 2) 跟踪 - 微分器的一般理论[2 ] 设二阶系统为 : x 1 = x 2 x 2 = u , u ≤ r 上式的“快速最优控制”综合系统为 : x 1 = x 2 x 2 = - rsgn ( x 1 + x 2 x 2 / (2 r) ) 把 x 1 ( t) 改为 x 1 ( t) - v ( t) ,得 x 1 = x 2 x 2 = - rsgn ( x 1 - v ( t) + x 2 x 2 / (2 r) ) (1) 式中 , x 1 ( t) 是在限制 ¨x 1 ≤r 下 ,最快地跟踪输 入信号 v ( t) 。 x 1 ( t) 充分接近 v ( t) 时 ,有 x 2 ( t) = x 1 ( t) 可做 v ( t) 的近似微分 。 定理 　设二阶系统为 : x 1 = x 2 x 2 = f ( x 1 , x 2) (2) 式中 , x 1 ( r , t) 跟踪 v ( t) , x 2 ( r , t) 收敛于“广义 函数”v ( t) 的“广义导数”。 系统式 (3) 称做系统式 (2) 派生的“跟踪微分 器”。 系统式 (1) 称做“快速跟踪微分器”。 3) “快速跟踪微分器”的离散形式 用跟踪微分器式 (1) 来进行数值计算 , 进入 “稳态”时易产生“高 频 颤 振”, 把 sgn ( x ) 改 成 sat ( x , d) 也不能使之避免 。为此 , 我们给出“跟 踪微分器”的离散形式 。 设离散系统为 : x 1 ( k + 1) = x 1 ( k) + hx 2 ( k) x 2 ( k + 1) = x 2 ( k) + hu , u ≤ r 直接对上式求“快速控制最优综合函数”,得 u = f st ( x 1 , x 2 , r , h) : d = rh ; d0 = dh ; y = x 1 + hx 2 ; a0 = ( d2 + 8 r y ) a = f st = - x 2 + ( a0 - d) / 2 , x 2 + y/ h , ra/ d , rsgn ( a) , a ≤ d a > d 1 2 ; y > d0 y ≤ d0 式中 , h 为积分步长 。 有离散系统为 : x 1 ( t + h) = x 1 ( t) + hx 2 ( t) x 2 ( t + h) = x 2 ( t) + hf st ( x 1 ( t) - (4) v ( t) , x 2 ( t) , r , h) 系统式 (4) 是很好的数值微分器 , 称做“快速离散 跟踪微分器”[3 ]　。把函数 f st (·) 中的变量 h 取成 与步长 h 相互独立的新变量 h0 ,得 x 1 ( t + h) = x 1 ( t) + hx 2 ( t) x 2 ( t + h) = x 2 ( t) + hf st ( x 1 ( t) - (5) v ( t) , x 2 ( t) , r , h0) 系统式 (5) 有两个可调参数 r , h0 。 r 决定跟踪速 度 ,称做“速度因子”; h0 起对噪声的滤波作用 ,称 做“滤波因子”。 注 1 :函数 f st ( x 1 , x 2 , r , h0) 在控制和信号处 若二阶系统式 (2) 稳定 ,那么对 t ∈[0 , + ∞) , T > 0 ,有系统 有界可测 v ( t) , 理中的作用非常广泛 。 x 1 = x 2 x 2 = r2 f ( x 1 - v ( t) , x 2/ r) (3) 且系统式 (3) 的解 x 1 ( r , t) 满足 r →∞∫T lim 0 x 1 ( r , t) - v ( t) d t = 0 4 　安排过渡过程 在一般的控制系统中 ,误差直接取成 : e = v - y 式中 , v 为设定值 ; y 为系统输出 。 误差的这种取法使初始误差很大 ,易引起“超
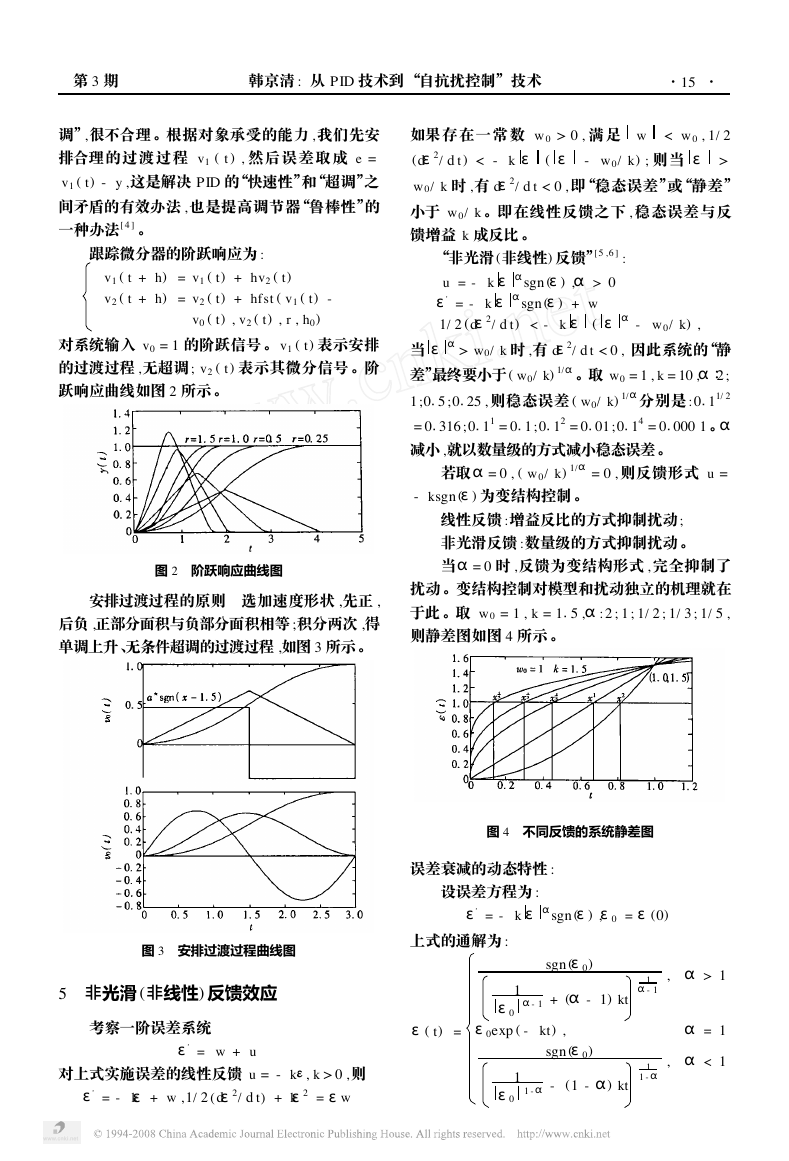
    ¾ ¾ 第 3 期 　　　　 　　　　韩京清 : 从 PID 技术到 “自抗扰控制”技术 ·51· 调”,很不合理 。根据对象承受的能力 , 我们先安 排合理的过渡过程 v 1 ( t ) , 然后误差取成 e = v 1 ( t) - y ,这是解决 PID 的“快速性”和“超调”之 间矛盾的有效办法 , 也是提高调节器“鲁棒性”的 一种办法[4 ] 。 跟踪微分器的阶跃响应为 : v 1 ( t + h) = v 1 ( t) + hv 2 ( t) v 2 ( t + h) = v 2 ( t) + hf st ( v 1 ( t) - v 0 ( t) , v 2 ( t) , r , h0) 对系统输入 v 0 = 1 的阶跃信号 。 v 1 ( t) 表示安排 的过渡过程 ,无超调 ; v 2 ( t ) 表示其微分信号 。阶 跃响应曲线如图 2 所示 。 如果存在一常数 w 0 > 0 , 满 足 w < w 0 , 1/ 2 (dε2/ d t ) < - k ε ( ε - w 0/ k) ; 则当 ε > w 0/ k 时 ,有 dε2/ d t < 0 , 即“稳态误差”或“静差” 小于 w 0/ k 。即在线性反馈之下 , 稳态误差与反 馈增益 k 成反比 。 “非光滑 (非线性) 反馈”[5 ,6 ] : u = - k ε αsgn (ε) ,α > 0 ε = - k ε αsgn (ε) + w 1/ 2 (dε2/ d t) < - k ε ( ε α - w 0/ k) , 当 εα > w 0/ k 时 ,有 dε2/ d t < 0 , 因此系统的“静 差”最终要小于 ( w 0/ k) 1/α。取 w 0 = 1 , k = 10 ,α∶2 ; 11/ 2 1 ;0 000 1 。α 25 , 则稳态误差 ( w 0/ k) 1/α分别是 :0 12 = 0 01 ;0 5 ;0 316 ;0 14 = 0 = 0 减小 ,就以数量级的方式减小稳态误差。 11 = 0 1 ;0 图 2 　阶跃响应曲线图 安排过渡过程的原则 　选加速度形状 ,先正 , 后负 ,正部分面积与负部分面积相等 ;积分两次 ,得 单调上升、无条件超调的过渡过程 ,如图 3 所示。 若取α= 0 , ( w 0/ k) 1/α = 0 , 则反馈形式 u = - ksgn (ε) 为变结构控制 。 线性反馈 :增益反比的方式抑制扰动 ; 非光滑反馈 :数量级的方式抑制扰动 。 当α= 0 时 ,反馈为变结构形式 , 完全抑制了 扰动 。变结构控制对模型和扰动独立的机理就在 5 ,α:2 ; 1 ; 1/ 2 ; 1/ 3 ; 1/ 5 , 于此 。取 w 0 = 1 , k = 1 则静差图如图 4 所示 。 图 4 　不同反馈的系统静差图 误差衰减的动态特性 : 设误差方程为 : ε = - k ε αsgn (ε) ,ε0 = ε(0) 上式的通解为 : sgn (ε0) 1 ε0 α- 1 + (α - 1) kt , α > 1 1 α- 1 ε( t) = ε0exp ( - kt) , sgn (ε0) 1 ε0 1 - α - (1 - α) kt 1 1 - α α = 1 , α < 1 图 3 　安排过渡过程曲线图 5 　非光滑 (非线性) 反馈效应 考察一阶误差系统 ε = w + u 对上式实施误差的线性反馈 u = - kε, k > 0 ,则 ε = - kε + w ,1/ 2 (dε2/ d t) + kε2 = εw
    ¾ ¾ ·61· 控 　制 　工 　程 　　　　　　 　　　　　　　　第 9 卷 1 - α 式中 , t ≤ ε0 / k (1 - α) 。当 α> 1 时 ,ε( t) 以 1/ ( kt) 1/ (α- 1) 的速 度 衰 减; 当 α = 1 时 ,ε( t ) 以 exp ( - kt) 的速 度“指 数 衰 减”; 当 α < 1 时 , 在 / k (1 - α) 时刻 ,ε= 0 ,即“有限时间衰 T = x0 减”到 0。 1 - α 这里α≥1 时是“光滑反馈”;α< 1 时是“非光 称为经典状态观测器。这两个系统的误差方程为 : ε = z - x ε = ( A - L C)ε 矩阵 A - L C 稳定时 , z ( t ) 渐近地估计状态变量 x ( t) 。如果 L 是依噪声特性按最小方差律确定 的 ,则这个状态观测器就是卡尔曼滤波器 。 滑反馈”;α= 0 时是“变结构控制”。 考虑系统 注 2 :“非光滑反馈”的效率比“光滑反馈”好 。 “光滑反馈”里 ,“指数衰减率”最好 ;“非光滑”反 馈里 ,“指数衰减率”最不好 。 6 　非线性 PID 利用跟踪微分器 ( TD) ,把经典 PID 改造成 “非线性 PID”,其结构如图 5 所示 。 图 5 　非线性 PID 结构图 这里 TD 给出跟踪输出 y 的量 z 1 及其微分 z 2 ;误差 、积分 、微分是由安排的过渡过程和 TD 的输出 z 1 , z 2 来产生的 。 z 1 , e0 =∫t e1 , e2 = v 2 - e1 = v 1 - z 2 = e1 0 把原先的“加权和”改成“非线性组合”而得“非线 性 PID”。一种可用的“非线性组合”形式为 : f al ( e ,α,δ) = αsgn( e) , e e/δ1 - α , e > δ, e ≤δ, δ > 0 当α< 1 时 , f al 函数具有 :小误差 , 大增益 ; 大误 差 ,小增益的特性 。 “非线性 PID”的控制律为[7 ] : u =β0 f al ( e0 ,α0 ,δ) +β1 f al ( e1 ,α1 ,δ) + β2 f al ( e2 ,α2 ,δ) 式中 ,α0 ≤α1 ≤α2 ,甚至可取 α0 < 0 , 0 <α1 ≤1 ,α2 ≥1 。也可采用其他合适的“非线性组合”。 7 　扩张状态观测器 ( ESO) 对于系统方程 x = A x + B u y = Cx x 1 = x 2 x 2 = f ( x 1 , x 2 , t) + bu (6) y = x 1 若 f ( x 1 , x 2 , t) 为已知 ,则其观测器可设计为 : ε1 = z 1 - y z 1 = z 2 - β01ε1 z 2 = f ( z 1 , z 2 , t) - β02ε1 + bu 问题 :很多情况下 f ( x 1 , x 2 , t ) 未知 , 因此不 能应用 f ( x 1 , x 2 , t ) , 那么如何构造状态观测器 呢 ? 当 f ( x 1 , x 2 , t) 未知时 ,把 f ( x 1 , x 2 , t ) 当作 扰动 ,用“非光滑反馈”效应抑制其作用 。 令 x 3 = f ( x 1 , x 2 , t ) , x 3 = g ( x 1 , x 2 , t ) , 则 g ( x 1 , x 2 , t) 也是未知函数 ,于是有 x 1 = x 2 x 2 = x 3 + bu x 3 = g ( x 1 , x 2 , t) y = x 1 ε1 = z 1 - y z 1 = z 2 - β01ε1 z 2 = z 3 - β02 f al (ε1 ,α1 ,δ) + bu z 3 = - β03 f al (ε1 ,α2 ,δ) (7) 式中 ,α2 <α1 ,可取α1 = 0 g ( x 1 , x 2 , t) < w 0 5 = 1/ 2 ,α2 = 0 25 = 1/ 4。 z 1 ( t) - x 1 ( t) < 1/α 2 , w 0 β03 z 2 ( t) - x 2 ( t) < β01 1/α 2 , w 0 β03 z3 ( t) - f ( x1 ( t) , x2 ( t) , t) < β02 lim t →∞ lim t →∞ lim t →∞ 1/α 2 w 0 β03 被扩张的状态 z3 ( t) 对“未知扰动”的“实时作用 量”a( t) = f ( x1 ( t) , x2 ( t) , t) 作出很好的估计。 系统式 (7) 叫做系统式 (6) 的“扩张状态观测 系统 z = A z - L ( Cz - y) + B u 器”[8 ] 。
    ¾ ¾ 第 3 期 　　　　 　　　　韩京清 : 从 PID 技术到 “自抗扰控制”技术 ·71· 若 f ( x1 , x2 , t) = f 0 ( x1 , x2) + f 1 ( x1 , x2 , t) , 态”和“未知外扰”作用一并给予估计和补偿[9 ] 。 f 0 ( x1 , x2) 已知 ,取 x3 = f 1 ( x1 , x2 , t) ,则有 “自抗扰控制器”算法 : z 1 = z2 - β01ε1 z 2 = z3 - β02 f al (ε1 ,α1 ,δ) + f 0 ( z1 , z2) + bu z 3 = - β03 f al (ε1 ,α2 ,δ) 式中 , f (·) 是系统的“内扰”和“外扰”的总和 , 即 系统的“总扰动”。 ESO 的 z 3 ( t) 估计的是“总扰动”中未知部分 的“实时作用量”a1 ( t) = f 1 ( x 1 ( t) , x 2 ( t) , t) 。 ( z 3 ( t ) + f 0 ( x 1 ( t ) , 当控 制 量 u = u0 - x 2 ( t) ) ) / b时 ,对象近似地变成为 : x 1 = x 2 x 2 = bu0 y = x 1 系统被“线性化”成“积分器串联型”。这是不确定 系统的“实时动态线性化”。 “系统设计”问题变成对“积分器串联型系统 的设计”问题 。 8 　自抗扰控制器 (Active Disturbance s Re jection Controller ,ADRC) 利用 TD 和 ESO ,给出如下 ADRC 控制器方 案 ,如图 6 所示 。 图 6 　ADRC 结构框图 当对象有已知部分 f 0 ( ·) 时 , ADRC 结构如 图 7 所示 。 图 7 　对象有已知部分时的 ADRC 结构框图 这里不再需要“误差积分”反馈 。“自抗扰”意 z 3 ( t ) / b , 系统的“未建模动 义在于”补偿”项 - 　被控对象 : ¨x = f ( x , 1) 安排过渡过程 v 0 为设定值 。 x , w , t) + bu , y = x v 1 ( k + 1) = v 1 ( k) + hv 2 ( k) v 2 ( k + 1) = v 2 ( k) + hf st ( v 1 ( k) - v 0 , v 2 ( k) , r , h0) 或其他合适办法 。 2) 估计状态和总扰动 ( ESO 方程) 　　ε1 = z 1 ( k) - y ( k) z 1 ( k + 1) = z 1 ( k) + h ( z 2 ( k) - β01ε1) z 2 ( k + 1) = z 2 ( k) + h ( z 3 ( k) - β02 f al (ε1 ,α1 ,δ) + bu ( k) ) z 3 ( k + 1) = z 3 ( k) - hβ03 f al (ε1 ,α2 ,δ) 3) 控制量的形成 z 1 ( k) , z 2 ( k) , e1 = v 1 ( k) - e2 = v 2 ( k) - u0 = β01 f al ( e1 ,α1 ,δ) +β02 f al ( e1 ,α2 ,δ) , u ( k) = u0 - z 3 ( k) / b , 式中 , f al (ε,α,δ) = ε αsgn (ε) , ε > δ, ε/δ1 - α ε ≤δ, , δ > 0 这个控制器的算法只需对象的输入输出数据 u ( k) 和 y ( k) 。 被控对象的函数 f ( x 1 , x 2 , t ) 有已知部分 f 0 ( x 1 , x 2) ,控制器算法中的 u ( k) 和 ESO 改为 : 　u ( k) = u0 - ( z 3 ( k) + f 0 ( z 1 ( k) , z 2 ( k) ) ) / b z 1 ( k + 1) = z 1 ( k) + h ( z 2 ( k) - β01ε1) z 2 ( k + 1) = z 2 ( k) + h ( z 3 ( k) - β02 f al (ε1 ,α1 ,δ) × f 0 ( z 1 ( k) , z 2 ( k) ) + bu ( k) ) z 3 ( k + 1) = z 3 ( k) - hβ03 f al (ε1 ,α2 ,δ) 9 　“控制问题”的描述 从自抗扰控制器的作用机理看 , 我们从另外 一个角度描述控制问题 。 从控制的目的来看 ,对于下面两个系统 ¨x = f ( x , x , w , t) + bu , y = x 和 ¨x = f ( t) + bu , f ( t) = f ( x ( t) , 它们的控制问题没有什么区别 。 x ( t) , w ( t) , t) , y = x ①被控对象 　以一定范围变化的 f ( t) 和输 入量 u 所驱动的动态系统为 :
    2 控 　制 　工 　程 　　　　　　 　　　　　　　　第 9 卷 2 ·81· 的集合 。 ¨x = f ( t) + bu , y ( t) = x ( t) 记 F = { f ( t) ‖f ( t ) | ≤F0} , F 为动态系统 ②控制目标 　输入 v 0 ( t) , | v 0 ( t) | ≤V 0 所 激励的一动态过程 ¨v = v 0 ( t) 的输出 v ( t) 所成的 集合 V 。 ③控制器 　以 v ( t) 、y ( t ) 、u ( t ) 为输入 、输 出 、控制量 , 且含有可调参数 p 的动态系统 , 用 C ( p) 表示 。 ④控制问题 　用{ F , V } 表示如下“控制问 题”:设计一控制器 C ( p) , 对 v ( t) ∈V ,控制器 C ( p) 所产生的控制量 u ( t ) , 都能使输出 y ( t) 跟踪目标 v ( t) 。 f ( t ) ∈ F 和 控制系统 ¨x = f ( t) + bu 的输出 y ( t) = x ( t) 要跟踪信号 v ( t ) , v ( t ) 是由信号发生器 ¨v = v 0 ( t) ,| v 0 ( t) | ≤V 0 产生的 。 记 M = F0 + | b| V 0 ,ρ= M - 1 2 , 则称 ρ为控 制系统的“时间尺度”。“时间尺度”的直观意义 为 :0 1 s 采样才能控制的问题的时间尺度比 1 s 采样才能控制的问题的时间尺度小 , 是表明系统 动作快慢的尺度 。 ADRC 需要的只是 ρ与 b 的粗略估计 , 不需 要 f ( x 1 , x 2 , t) 的具体形式 。有了 ρ与 b 的粗略 估计 ,控制器的参数也被确定了 。 10 　结 　语 本文从传统的 PID 原理及其结构进行分析 , 揭示了传统 PID 的优缺点 ,并本着继承其优点 , 克服其缺点的原则 ,逐步阐述了自抗扰控制技术 的基本思想 。这项新的控制技术的核心是把系统 的未建模动态和未知外扰作用都归结为对系统的 “总扰动”而进行估计并给予补偿 。采用的方法是 充分运用特殊的“非线性”效应 。 这种方法具有如下诸多优点 :安排过渡过程 解决了“快速性和超调之间的矛盾”;不用 I 反馈 也能实现“无静差”,避免了积分反馈的副作用 ;统 一处理确定系统和不确定系统的控制问题 ;不存 在“鲁棒性”问题 ,只有控制器的“鲁棒性”、“适应 范围”;抑制外扰 ,不一定要知道其模型或要直接 测量 ;同一个 ADRC 控制“时间尺度”相当的一类 对象 ;线性 、非线性对象一视同仁 ,不用区分 ;实现 控制 ,不一定要进行“辨识”;解耦控制 ,只需考虑 “静态耦合”,不用考虑“动态耦合”;ADRC 容易控 制时滞系统等 。 在 ADRC 技术中 ,“系统分类”不再是传统的 线性 、非线性 、时变 、时不变 ,而是按系统的“时间 尺度”来进行分类的 。 参考文献 : 1 2 3 4 5 6 7 8 9 G. J . Silva , A. Datta , S. P. Bhattacharyya. New Re sults on the Synthesis of PID Controllers J . IEEE Transactions on Automatic Control , 2002 , 47 ( 2) : 241 - 252. 韩京清 ,王伟. 非线性跟踪微分器 J . 系统科学 与数学 , 1994 ,4 (2) :177 - 183. 韩京清 ,袁露林. 跟踪微分器的离散形式 J . 系 统科学与数学 , 1999 ,19 (3) :268 - 273. 黄焕袍 ,万辉 ,韩京清. 安排过渡过程是提高闭环 系统“鲁棒性 、适应性和稳定性”的一种有效方法 J . 控制理论和应用 , 2001 ,18 (增) :89 - 94. 韩京清. 反馈系统中的线性和非线性 J . 控制与 决策 , 1988 ,3 (2) :27 - 32. 韩京清. 控制系统的非光滑综合 C . 中国控制会 议论文集. 香港 :香港城市大学 ,2000. 韩京清. 非线性 PID 控制器 J . 自动化学报 , 1994 ,20 (4) :487 - 490. 韩京清. 一类不确定对象的扩张状态观测器 J . 控制与决策 , 1995 ,10 (1) :85 - 88. 韩京清. 自抗扰控制器及其应用 J . 控制与决 策 , 1998 ,13 (1) :19 - 23. 10 韩京清. 线性系统的结构与反馈系统计算 C . 全 国控制理论及其应用会议论文集 , 北京 :科学出版 社 , 1981. 11 韩京清. 控制理论 模型论还是控制论J . 系统科 学与数学 , 1989 ,9 (4) :328 - 335. 12 韩京清. 非线性状态误差反馈控制律 NL SEF J . 控制与决策 , 1995 ,10 (3) :221 - 225. 13 韩京清 ,张文革. 大时滞系统的自抗扰控制 J . 控制与决策 , 1999 ,14 (4) :354 - 358. From PID Technique to Active Disturbances Rejection Control Technique ( Institute of Systems Science , AMSS , CAS , Beijing 100080 , China) HA N Ji ng qi ng Abstract : In this paper , advantages and disadvantages of classical PID are investigated from its basic principles. A new type Active Disturbances Rejection Controller (ADRC) with excellent characters is constructed via some links with especial controller functions ,such as Tracking Differentiator ( TD) , Extended States Observer( ESO) and Nonlinear PID(NPID) ,which are based on the nonlinear control mechanisms. Furthermore , the new active disturbances rejection control technique is formed. The new controller possesses the following characteristics :the algorithm is simple ; the adjustment of the parameters is easier. Key words :PID ; nonlinear feedback ; active disturbances rejection control
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料