基于内模控制的直流伺服电机分数阶控制方案的设计与验证2019.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：1.20M 资料格式：pdf 举报版权申诉

anbeijinwu-11449472-4744300845190653226.pdf-第1页.png

第1页 / 共13页

anbeijinwu-11449472-4744300845190653226.pdf-第2页.png

第2页 / 共13页

anbeijinwu-11449472-4744300845190653226.pdf-第3页.png

第3页 / 共13页

anbeijinwu-11449472-4744300845190653226.pdf-第4页.png

第4页 / 共13页

anbeijinwu-11449472-4744300845190653226.pdf-第5页.png

第5页 / 共13页

anbeijinwu-11449472-4744300845190653226.pdf-第6页.png

第6页 / 共13页

anbeijinwu-11449472-4744300845190653226.pdf-第7页.png

第7页 / 共13页

anbeijinwu-11449472-4744300845190653226.pdf-第8页.png

第8页 / 共13页

文本预览

IETE Technical Review ISSN: 0256-4602 (Print) 0974-5971 (Online) Journal homepage: https://www.tandfonline.com/loi/titr20 Design and Validation of Fractional-Order Control Scheme for DC Servomotor via Internal Model Control Approach Sahaj Saxena & Yogesh V. Hote To cite this article: Sahaj Saxena & Yogesh V. Hote (2019) Design and Validation of Fractional- Order Control Scheme for DC Servomotor via Internal Model Control Approach, IETE Technical Review, 36:1, 49-60, DOI: 10.1080/02564602.2017.1396935 To link to this article: https://doi.org/10.1080/02564602.2017.1396935 Published online: 06 Dec 2017. Submit your article to this journal Article views: 134 View Crossmark data Citing articles: 2 View citing articles Full Terms & Conditions of access and use can be found at https://www.tandfonline.com/action/journalInformation?journalCode=titr20

IETE TECHNICAL REVIEW 2019, VOL. 36, NO. 1, 49–60 https://doi.org/10.1080/02564602.2017.1396935 Design and Validation of Fractional-Order Control Scheme for DC Servomotor via Internal Model Control Approach Sahaj Saxena and Yogesh V. Hote Department of Electrical Engineering, Indian Institute of Technology Roorkee, Roorkee, India ABSTRACT This paper proposes a robust fractional-order controller for DC servomotor using internal model control and CRONE (Commande Robuste d’Ordre Non Entier) principle. The controller acquires a PID (proportional-integral-derivative) form followed by a fractional-order integrator. Unlike the conventional fractional-order PID controller which demands ﬁve tuning parameters, the proposed scheme has only two tuning parameters which can be obtained on the basis of desired gain crossover frequency and phase margin. For speed control problem, the performance of the proposed controller is studied on hardware set up called precision modular servo system. The proposed controller outperforms in terms of robustness and optimality when compared with controllers designed by integer-order technique. Furthermore, the proposed scheme is applied for position control problem and validated on QUBE-Servo 2 set up. KEYWORDS Fractional-order controller; Gain crossover frequency; Internal model control; Phase margin; PID control; Servomotor 1. INTRODUCTION etc. The DC servomotor has been used as a classical control example for nearly half a century because it is a standard i.e. second-order system with stable characteristics ( speed-torque characteristics are well suited with most mechanical loads) and has high industrial applicability (particularly in performance drives of rolling mills, machine tools, traction, robotics, ). Many control ideas have been developed and illustrated for this sys- tem, such as pulse width modulation and thyristor based control [1,2], variable structure system control [3,4], optimal control based on Pontryagin’s minimum princi- ple [5], H1 control [6], minimum energy point-to-point motion planning control [7], adaptive control [8], neural network [9,10], Fuzzy PID [11], feedback linearization scheme [12], estimation of distribution scheme [13], dis- turbance observer scheme [14], model predictive control [15,16], model-free control [17], algebraic derivation estimation-based control [18], integral retarded algo- rithm [19], stability boundary locus [20] and reduced modeling [21] based PID tunings and many more. Interest in the DC servomotor control has been renewed when recent developments have been made in the ﬁeld of fractional-order control theory. Actually, the frac- tional-order controller is more ﬂexible and gives a chance to improve dynamic properties of the fractional- order control system. In this regard, some control tech- niques have been proposed and veriﬁed experimentally for the tracking control and load regulation of the DC © 2019 IETE servomotor [22–28]. These controller schemes are based on reset control, state feedback control, model reference and fractional-order PID controller tuned via speciﬁed gain and phase margins. Since fractional calculus requires a lot of mathematical analysis, manipulations and approximations, therefore the above stated frac- tional-order controller strategies are complex in nature. Thus, it could be challenging task when their synthesis and implementation come into the picture. Having these facts in mind, our goal is to design a robust fractional-order controller through simple approach without dealing with complex mathematical computa- tion and synthesis method. Our work is motivated by the precious work of Ma^amar & Rachid [29] which bridges internal model control (IMC) and CRONE prin- ciples to derive fractional-order controller similar to PID form. Although the work of [29] opens a new dimension to produce a simple analytical fractional-order PID for ﬁrst- and second-order stable minimum and non-mini- mum phase plant, however the hardware validation is still missing in literature. In this paper, we deal with speed and position control problem of DC servomotor using fractional-order con- troller which includes PID controller and a fractional- order integrator. The proposed controller synthesis relies on CRONE approach and the popular IMC strategy which has a rich history [30–32]. On one hand, CRONE approach guarantees the phase ﬂatness condition, the i.e.

50 S. SAXENA AND Y. V. HOTE: DESIGN AND VALIDATION OF FRACTIONAL-ORDER CONTROL SCHEME phase of the loop transfer function is ﬂat at the gain crossover frequency thereby guaranteeing the invariance of the phase margin with respect to the process DC-gain variation such as pay-load, ampliﬁer feed forward gain and the load current/resistance in power systems. On the other hand through IMC strategy, the PID controller is tuned by a single parameter unlike three parameters in traditional PID controllers. Also, on the contrary to the conventional fractional-order PID controllers which require ﬁve parameters, the proposed scheme requires only two tuning parameters. The tuning law is based on the desired gain crossover frequency and phase margin. The proposed scheme is veriﬁed experimentally on hard- ware set-up of DC servomotor for speed control prob- lem. It is observed that the dynamic properties of the closed-loop with the proposed fractional-order control- ler are better than that of the closed-loop with the inte- ger-order controller. Moreover, the controller brings optimality in terms of integral error speciﬁcation. The proposed scheme is further extended to position control problem and validated on QUBE-Servo 2 set up. The other contribution in this paper comes in the form of evaluation of the robustness of the control loop. We know that the CRONE control principle yields robustness against plant perturbation but the limit of the plant uncertainty is not directly evaluated through this method. To fulﬁll this gap, we have derived the condition which provides the limit of uncertainty in the plant gain varia- tion to maintain the robust performance of controller. 2. PROBLEM FORMULATION The armature controlled DC servomotor model, as shown in Figure 1, has been studied by many authors, to analyse and optimize its functionality. Its linearized elec- tromechanical dynamics1 can be described as Figure 2: Unity feedback conﬁguration where ia is the armature winding current, v is the rotor angular speed, R is the armature winding resistance, L is the armature winding inductance, Kb is the back electro- motive force constant, u is the armature winding input voltage, Kt is the torque constant, J is the system moment of inertia, and d is the system damping coefﬁcient. From (1) and (2), the DC motor can be expressed in a linear time invariant and single-input single-output (SISO) system and can be described by a rational proper trans- fer function: P sð Þ ¼ v sð Þ u sð Þ ¼ Kt JLs2 þ JR þ dL Þs þ dR þ KbKt ð ð Þ In PMS set-up, an additional conversion gain h is commissioned with P sð Þ. Therefore, the complete model can now be written as: P sð Þ ¼ K Þs þ dR þ KbKt JLs2 þ JR þ dL (3) ð ð Þ where K = hKt. Here, our objective is to provide a syn- thesis method to design a controller C(s) in a feedback conﬁguration (see Figure 2) such that the DC motor tracks the reference speed without steady-state error and meets speciﬁed control performance. Thus, it is a track- ing problem in which we need limt ! 1 v tð Þ ¼ vf for all D where D is disturbance. d dt d dt ia ¼ R L v ¼ d J ia Kb L v þ Kt J v þ 1 L u ia 3. THEORETICAL BACKGROUND FOR CONTROLLER DESIGN In this section, we present and analyse some principles that characterize and help in formulating the controller. (1) (2) 3.1 Fractional-Order System The fractional calculus is a generalization of integration and derivation to non-integer order operators. The con- cept of fractional-order mathematics and system were planted over 300 years ago, however its potential appli- cations are traced out from past two decades [33–36]. These days in control system design, the fractional-order based strategy has become an active ﬁeld of research but still it is in initial phase and many aspects are yet to be Figure 1: Schematic of DC servomotor model

S. SAXENA AND Y. V. HOTE: DESIGN AND VALIDATION OF FRACTIONAL-ORDER CONTROL SCHEME 51 explored. In fractional-order system, the equations gov- erning the dynamics of system are of arbitrary order par- ticularly in fraction and for realization purpose, the building blocks of fractional-order system are fractional- order integrators and differentiators. Deﬁnition 3.1: The transfer function of fractional-order integrator is deﬁned as ; x 2 0; 1ð Þ: G sð Þ ¼ 1 (4) sx For x = 1, G(s) is a simple pure integrator. Also as x decreases towards 0, the effect of integration opera- tion eliminates since s0 = 1. Further, the addition of pure integrator retards the speed of response. At this stage, this the constraint. fractional-order integrator relaxes The spectral transfer function of (4) is G jVð þ jsin xp Þ ¼ Vx cos xp 2 1 2 Þ ¼ 1 Vx which yields The magnitude of (5) is A Vð M Vð Þ ¼ 20xlog Vð Þ and the phase is given by f Vð Þ ¼ arg x 1 Vx j ¼ x p 2 (5) (6) (7) Equations (6) and (7) state that the magnitude of a frac- tional-order integrator in the frequency domain drops at a rate of 20x dB/dec and its phase is xp/2 throughout the domain. On the contrary, the integer-order integrator yields ﬁxed drop at a rate of ¡20 dB/dec in magnitude and ¡p/2 in phase response. This may hinders the sta- bility and robustness of the closed-loop system. Thus, the fractional-order integer introduces the ﬂexibility for the controller design. With this, let us deﬁne a frac- tional-order system. Deﬁnition 3.2: The transfer function of strictly proper fractional-order system2 is deﬁned as 1P m i¼1 aisyi G sð Þ ¼ z sð Þ w sð Þ ¼ where am 6¼ 0 and ym > ym ¡ 1 > ... > y1 > 0. In time domain, (8) corresponds to Xm t z tð Þ ¼ w tð Þ aiDyi i¼1 (8) where Dv 0Dv is Caputo’s fractional derivative of order v with respect to variable t and with the starting point at t = 0: t t z tð Þ ¼ 0Dv 1 G n v ð Þ Z t 0 z nð Þ tð Þ Þvn1 dt; 8 n 1 < v < n t t ð (9) where z(n)(t) is the nth derivative of z(t) with respect to t, n 2 N and G() is Gamma function. The Laplace trans- form of fractional derivative deﬁned by (9) is Z1 stDvz tð Þdt ¼ svz sð Þ svk1z kð Þ 0ð Þ; 8 n 1v < n Xn1 k¼0 e 0 Remark 3.1: In Caputo deﬁnition, initial conditions are of integer-order which make them easier to interpret because the integer-order derivatives of involved varia- bles have well-established physical meanings and can be easily obtained by experimental means. 3.2 CRONE Control The CRONE control methodology is a frequency domain approach which involves fractional integration in accordance to the Bode’s ideal transfer function for- mat. It relies on the concept of robustness in order to maintain time and frequency domain performance measures like iso-damping property and stability margin [37,38]. In CRONE principle, the open-loop transfer function is deﬁned by fractional-order integrator. Let us consider a conventional feedback control system (of Figure 2) with open-loop transfer function L sð Þ C sð ÞG sð Þ ¼ k sa ; 1 < a < 2; k > 0: (10) Therefore for (10), the gain crossover frequency is given by Vgc ¼ k1=a: (11) The open-loop Bode diagrams of amplitude and phase have slope of ¡20a dB/dec and a constant phase of ¡0.5ap, respectively. The closed-loop transfer function for (10) is given by T sð Þ L sð Þ 1 þ L sð Þ ¼ 1 1 þ sa=k (12)

52 S. SAXENA AND Y. V. HOTE: DESIGN AND VALIDATION OF FRACTIONAL-ORDER CONTROL SCHEME Remark 3.2: The order a and Vgc establish the over- shoot and the speed of the output response, respectively. Therefore for (12), T(s) has phase margin f ¼ p 1 0:5a which is independent of system gain k. Further, the spec- tral transfer function of (12) is (13) Þ; ð T jVð Þ ¼ þ j Vasin ap k 2 k þ Vacos ap 2 whose magnitude is given by jT jVð Þj ¼ q ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ k2 þ V2a þ 2kVacos ap k 2 2 2 i.e. sinap 2 Now, to investigate the behaviour in frequency domain, we evaluate the resonance peak Mr = maxjT(jV)j at res- ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ q onance frequency Vr. Here, jT(jV)j is maximum when k2 þ V2a þ 2kVacos ap its denominator term, C is minimum. To obtain the minimum value of C, set dV C ¼ 0 which yields Vr ¼ kjcos ap j1 d a. On substituting this value in jT(jV)j, we get Mr ¼ 1 . Since Mr is an indicative of maximum overshoot which is independent of k and depends only on a. Thus, the CRONE principle guarantees the robustness of controller against gain uncertainties in the plant. Therefore, the closed-loop sys- tem (12) could be used as reference model to design C(s) according to desired performance speciﬁcations using Vgc and f. Remark 3.3: Unlike the popular robust H1 scheme where over estimation is made in parametric uncertainty, this CRONE control considers the genuine uncertainty and thus explicitly ensures the robustness of the control loop. 3.3 IMC Scheme The IMC strategy relies on the internal model principle in which the plant model P sð Þ is arranged in a special conﬁguration as shown in Figure 3 [30–32]. The IMC controller is deﬁned by Q sð Þ ¼ P 1 sð ÞF sð Þ (14) The output is formulated as 1 þ Q sð ÞDP sð Þ vf sð Þ þ 1 Q sð ÞP sð Þ v sð Þ ¼ Q sð ÞP sð Þ where DP sð Þ ¼ P sð Þ P sð Þ is the plant-model mis- match. 1 þ Q sð ÞDP sð Þ D sð Þ (15) Figure 3: IMC conﬁguration Remark 3.4: Since no plant model is perfect, a low-pass ﬁlter F(s) is generally augmented with the inverse of the plant to reduce the inﬂuence of high-frequency model- ling errors. i.e. v(s) = vf(s) for all Remark 3.5: The perfect control, D(s), is achieved when P sð Þ ¼ P sð Þ and F(s) = 1. Remark 3.6: Under perfect control, when SISO stable P (s) and P sð Þ are employed, then the closed-loop control system is internally stable when Q(s) is stable. The IMC structure is complex for practical implementa- tion, and it is usually rearranged into its equivalent con- ventional unity feedback control structure as shown in Figure 2. The relation between Q(s) and C(s) is given by C sð Þ ¼ Q sð Þ 1 Q sð ÞP sð Þ (16) Remark 3.7: The equivalent conventional feedback con- trol structure is stable because the IMC structure is inter- nally stable. Theorem 3.1: [32] Assume a minimum-phase plant G(s) and its model ~G sð Þ. Under perfect control, the closed-loop transfer function derived using IMC strategy is the trans- fer function of the IMC ﬁlter used. 4. PROPOSED CONTROL SCHEME In this section, we design the fractional-order controller for servomotor system represented by (3). Then we prove that the proposed controller is capable of follow- ing desired speed. 4.1 Controller Formulation For designing controller for (3), the IMC ﬁlter is selected in the fractional-order form as F sð Þ ¼ 1 1 < b < 2 (17) ; 1 þ λsb where λ denotes ﬁlter time-constant which maintains speed of response and robustness. From (14), the IMC

S. SAXENA AND Y. V. HOTE: DESIGN AND VALIDATION OF FRACTIONAL-ORDER CONTROL SCHEME 53 controller is obtained as ð Q sð Þ ¼ JLs2 þ JR þ dL Þ ð K 1 þ λsb ð Þs þ dR þ KbKt Þ ð Substituting (18) in (16), we get ð Þs þ dR þ KbKt C sð Þ ¼ JLs2 þ JR þ dL Kλs sg kp þ ki 1 s Þ 1 sb1 þ kds (18) (19) where g ¼ b 1; kp ¼ JR þ dL Kλ ; ki ¼ dR þ KbKt Kλ ; kd ¼ JL Kλ (20) Equation (19) yields controller which is a PID controller cascaded with an additional fractional-order integrator. 4.2 Controller Tuning i.e. The controller in (19) has two unknown variables called λ and g. To evaluate these tuning tuning parameters, parameter, Theorem 3.1 is employed which illustrates that T(s) = F(s). Therefore, F(s) of (17) can be treated as a reference model (12) for applying CRONE principle. Now on comparing (17) with (12) , we have a = b and k ¼ 1 λ. Upon substituting these values of a and k in (11) and (13), the tuning parameter is obtained as λ ¼ 1=Vb Since, g = b ¡ 1, we have g ¼ p f 0:5p 1 (21) (22) gc : Thus, with the desired speciﬁcations Vgc and f, tuning can be achieved. 4.3 Tracking Capability Now, our goal behaviour of the proposed controller. is to observe and study the tracking Corollary 4.1: Under the assumption of zero plant-model mismatching, the steady-state error e(t) for unit step input to the closed-loop system is zero when IMC ﬁlter F(s) described in (17) is used to design IMC based controller. Proof: From Theorem 3.1, the complementary sensitiv- the closed-loop transfer function is T(s) ity function, = F(s). It the sensitivity i.e. immediately follows that function (transfer function from error signal to output) S(s) 1 ¡ T(s) is S sð Þ ¼ λsb 1 þ λsb (23) S sð Þ If E(s) be the Laplace transform of e(t) then E sð Þ ¼ 1 s On substituting (23) in (24) and applying “ﬁnal value theorem” of signal and systems [39], we get t ! 1 e tð Þ ¼ lim s! 0 sE sð Þ ¼ 0 (24) (25) lim Thus, Corollary 4.1 proved that at steady-state, the error signal converges to zero and the output follows the step input. Hence, this control scheme ensures (i) zero steady-state error, (ii) iso-damping3 property of the closed-loop step response and (iii) robustness against process gain variation. 5. EXPERIMENTAL RESULTS To illustrate the efﬁciency of the proposed methodology, the experiment is performed on a laboratory-scale set-up called PMS system developed by Feedback Instruments Limited, UK. The set-up allows testing of designed con- trollers in real time in Hardware-in-Loop conﬁguration. 5.1 System description PMS set-up, as shown in Figure 4, is basically a DC ser- vomotor equipped with velocity and position measure- ment unit and motor driver4. The set-up is controlled with the personal computer in MATLAB environment using FOMCON toolbox available at http://fomcon.net/ fomcon-toolbox/download/. The fractional derivative has been implemented by the Oustaloup recursive ﬁlter Figure 4: PMS set-up

54 S. SAXENA AND Y. V. HOTE: DESIGN AND VALIDATION OF FRACTIONAL-ORDER CONTROL SCHEME approximation5 choosing a frequency range of [Vl, Vh] ¡3, 103] rad/s and order of ﬁlter N = 5. The maxi- = [10 mum value of control signal from computer is ¡2.5V to +2.5V. The motor used is a 24V DC brushed motor with a no-load maximum speed of 4050 rpm and nominal torque at 2A is in the order of 0.1 N-m. The typical val- ues of the parameters of the DC motors are as follows: J = 140 £ 10 ¡7 kg m2, Kt = 0.052 Nm/A, Kb = ¡6 Nms/rad, R = 2.5V, L =2.5 mH, 0.057 Vs/rad, d = 10 and h = 288/p. We want to apply the proposed method- ology by considering following speciﬁcations: (1) Vgc = 1 rad/s and (2) f = p/3. 5.2 Performance Analysis On substituting the parameters of motor deﬁned in (19), we obtained the proposed controller in which we get λ = 1 and g ¼ 1 3 from (21) and (22), respectively. To test the efﬁciency of controller, PID controller is designed using conventional IMC approach [30]. The controller param- eters are enlisted in Table 1. The performance of control- Table 1: Controller parameters Method Proposed IMC kp 7.3421 £ 10 7.3 £ 10 ¡3 ¡6 ki 6.2232 £ 10 ¡4 0.6223 kd 7.3421 £ 10 ¡9 7.3421 £ 10 ¡6 FO-IMC IMC 0.5 1 1.5 t (s) (a) 2 2.5 3 FO-IMC IMC ler is tested for four different cases. In all the cases, the reference speed vf is set to 1000 rad/s. 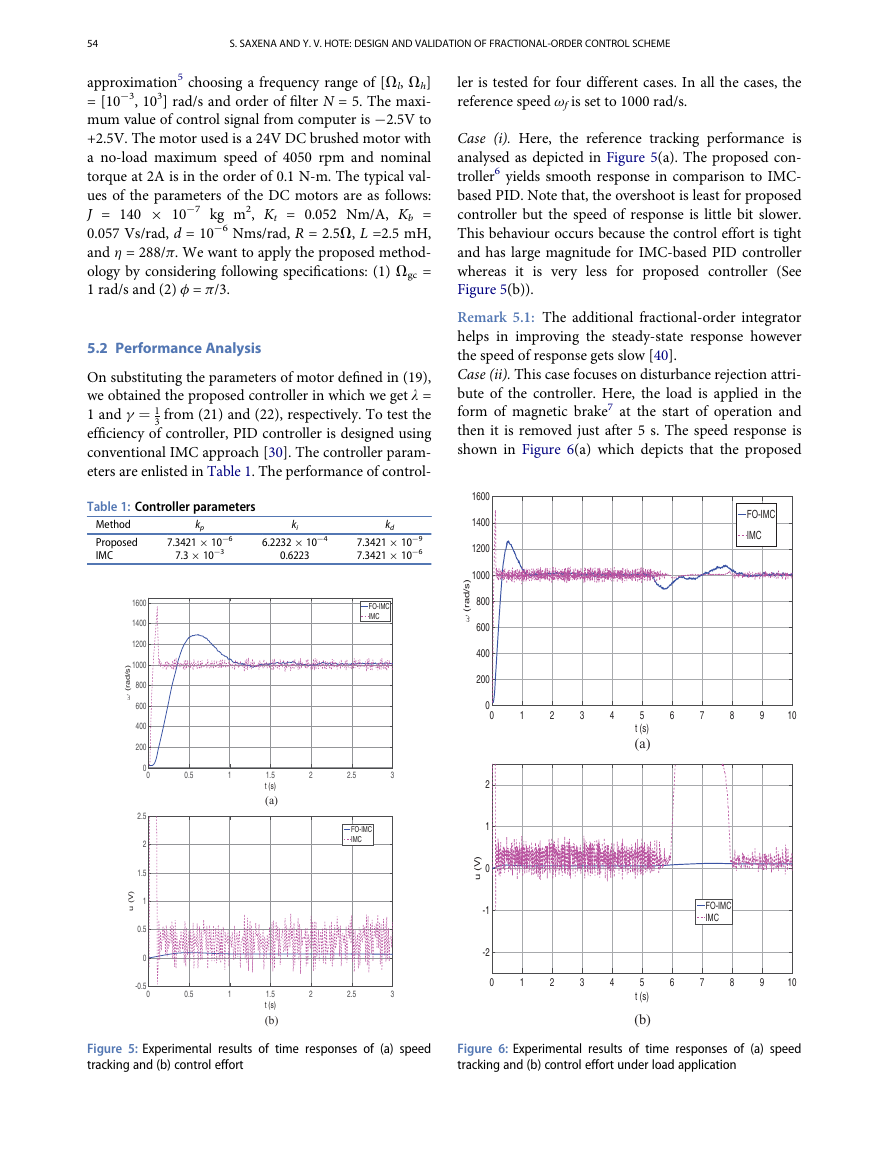Case (i). Here, the reference tracking performance is analysed as depicted in Figure 5(a). The proposed con- troller6 yields smooth response in comparison to IMC- based PID. Note that, the overshoot is least for proposed controller but the speed of response is little bit slower. This behaviour occurs because the control effort is tight and has large magnitude for IMC-based PID controller whereas it is very less for proposed controller (See Figure 5(b)). Remark 5.1: The additional fractional-order integrator helps in improving the steady-state response however the speed of response gets slow [40]. Case (ii). This case focuses on disturbance rejection attri- bute of the controller. Here, the load is applied in the form of magnetic brake7 at the start of operation and then it is removed just after 5 s. The speed response is shown in Figure 6(a) which depicts that the proposed ) s / d a r ( ω 1600 1400 1200 1000 800 600 400 200 0 0 FO-IMC IMC 1 2 3 4 5 t (s) (a) 6 7 8 9 10 ) V ( u 2 1 0 -1 -2 FO-IMC IMC 1600 1400 1200 1000 800 600 400 200 ) s / d a r ( ω 0 0 2.5 2 1.5 ) V ( u 1 0.5 0 -0.5 0 0.5 1 1.5 t (s) (b) 2 2.5 3 0 1 2 3 4 5 t (s) (b) 6 7 8 9 10 Figure 5: Experimental results of time responses of (a) speed tracking and (b) control effort Figure 6: Experimental results of time responses of (a) speed tracking and (b) control effort under load application

S. SAXENA AND Y. V. HOTE: DESIGN AND VALIDATION OF FRACTIONAL-ORDER CONTROL SCHEME 55 1400 1200 1000 800 600 400 200 ) s / d a r ( ω 0 0 0.5 1 1400 1200 1000 800 600 400 200 ) s / d a r ( ω 0 0 0.5 1 1.5 t (s) (a) 1.5 t (s) (b) In continuation to reference and disturbance rejection performance, the optimal performance is also measured. In this paper, integral of the time weighted absolute error (ITAE) Z1 ITAE ¼ tje tð Þjdt (26) −20% +50% 2 2.5 3 −20% +50% 2 2.5 3 0 is selected to study the optimal behavior of the control- ler. The ITAE index emphasizes on a long duration error. From Table 2, it is observed that for all cases except the Case (iv), the proposed controller produces the least value of ITAE. For Case(iv), it yields slightly higher value than that of IMC. Thus, it can be concluded that the proposed controller scheme brings optimality. 5.3 Stability Analysis In the sequence of analysing the performance of con- trolled system, stability is another essential part. Unlike the stability analysis of integer-order system, the analysis of fractional-order system is done in different fashion. The stability of fractional-order system can be investi- gated through the Matignon’s stability theorem as stated below. 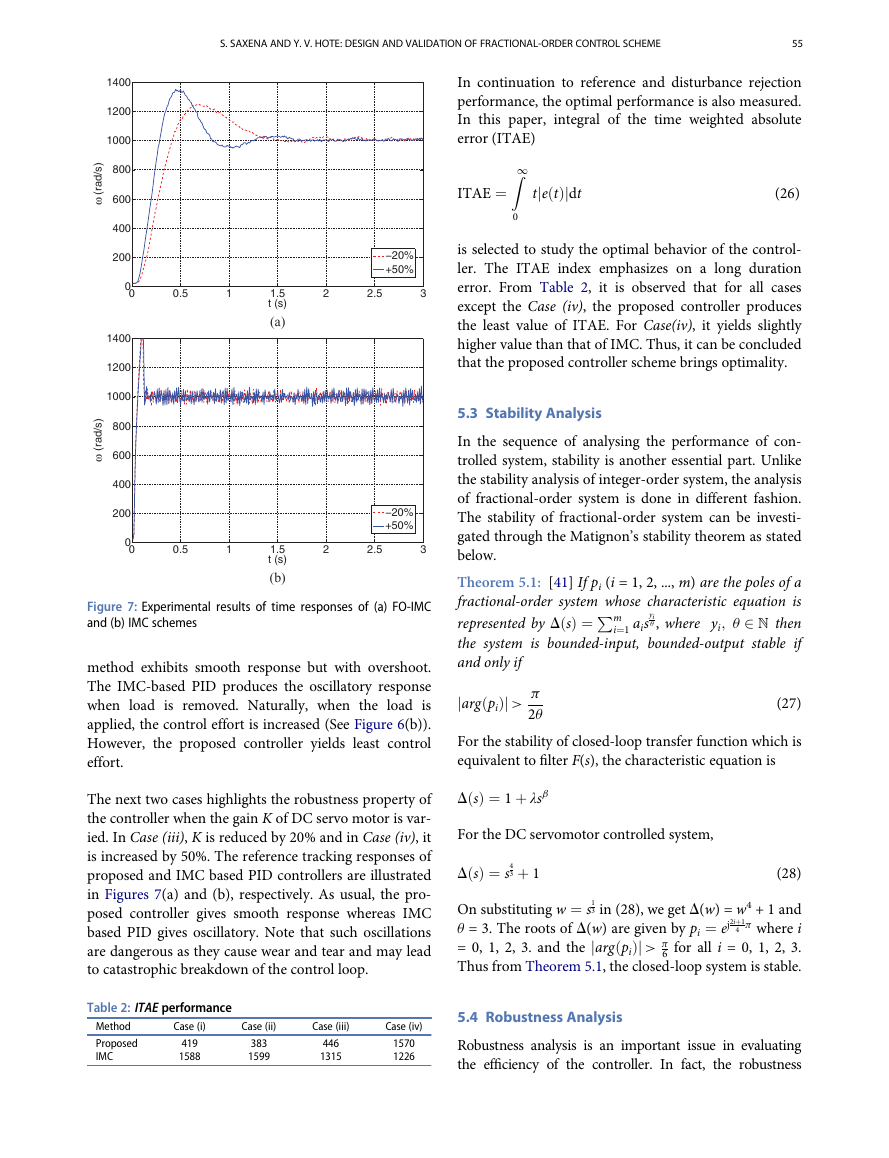Figure 7: Experimental results of time responses of (a) FO-IMC and (b) IMC schemes method exhibits smooth response but with overshoot. The IMC-based PID produces the oscillatory response when load is removed. Naturally, when the load is applied, the control effort is increased (See Figure 6(b)). However, the proposed controller yields least control effort. The next two cases highlights the robustness property of the controller when the gain K of DC servo motor is var- ied. In Case (iii), K is reduced by 20% and in Case (iv), it is increased by 50%. The reference tracking responses of proposed and IMC based PID controllers are illustrated in Figures 7(a) and (b), respectively. As usual, the pro- posed controller gives smooth response whereas IMC based PID gives oscillatory. Note that such oscillations are dangerous as they cause wear and tear and may lead to catastrophic breakdown of the control loop. represented by D sð Þ ¼P Theorem 5.1: [41] If pi (i = 1, 2, ..., m) are the poles of a fractional-order system whose characteristic equation is u , where yi; u 2 N then the system is bounded-input, bounded-output stable if and only if jarg pið Þj > yi m i¼1 ais (27) p 2u For the stability of closed-loop transfer function which is equivalent to ﬁlter F(s), the characteristic equation is D sð Þ ¼ 1 þ λsb 3 þ 1 For the DC servomotor controlled system, D sð Þ ¼ s4 On substituting w ¼ s1 3 in (28), we get D(w) = w4 + 1 and u = 3. The roots of D(w) are given by pi ¼ ej2iþ1 p where i = 0, 1, 2, 3. and the jarg pið Þj > p 6 for all i = 0, 1, 2, 3. Thus from Theorem 5.1, the closed-loop system is stable. (28) 4 Table 2: ITAE performance Method Proposed IMC 419 1588 Case (i) Case (ii) Case (iii) Case (iv) 383 1599 446 1315 1570 1226 5.4 Robustness Analysis Robustness analysis is an important issue in evaluating the efﬁciency of the controller. In fact, the robustness

分享到：

赞收藏

资料库

基于内模控制的直流伺服电机分数阶控制方案的设计与验证2019.pdf

相关推荐

课程资源

热门标签

最新资料