logo资料库

语音回声消除与LMS自适应滤波算法.pdf

发布时间：2022-06-10 发布人：admin 分类：说明书 资料大小：0.49M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    语音回声消除与LMS自适应滤波算法 Matlab回声消除资料 http://cn.mathworks.com/help/dsp/examples/acoustic-echo-cancellation-aec.html?requestedDomain=www.mathworks.com 第一遍迭代先做语音活动检测 https://github.com/wavesaudio/Speex-AEC-matlab http://dl.acm.org/citation.cfm?id=1283356 从通讯回音产生的原因看，可以分为声学回音（Acoustic Echo）和线路回音（Line Echo），相应的回声消除技术就叫声学回声消除 （Acoustic Echo Cancellation，AEC）和线路回声消除（Line Echo Cancellation, LEC）。声学回音是由于在免提或者会议应用中，扬声器的 声音多次反馈到麦克风引起的（比较好理解）；线路回音是由于物理电子线路的二四线匹配耦合引起的（比较难理解）。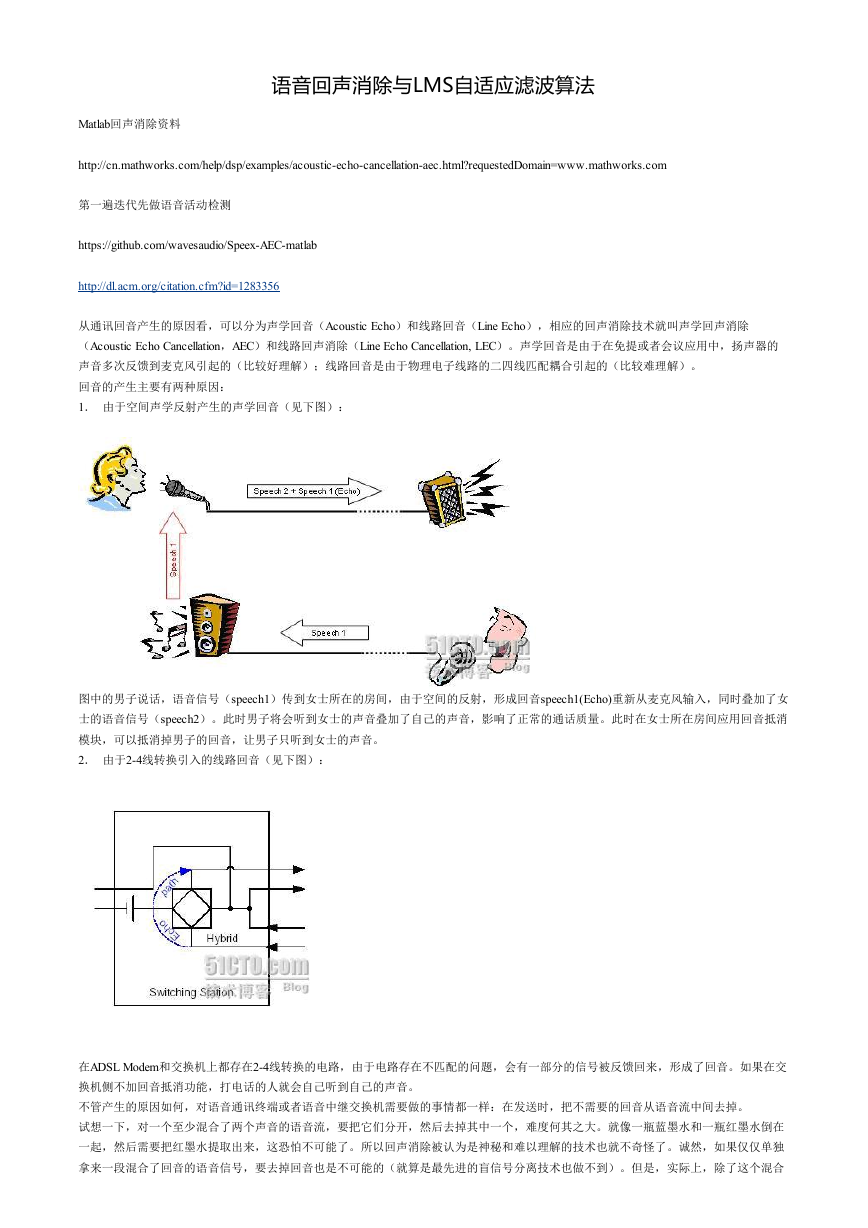 回音的产生主要有两种原因： 1． 由于空间声学反射产生的声学回音（见下图）： 图中的男子说话，语音信号（speech1）传到女士所在的房间，由于空间的反射，形成回音speech1(Echo)重新从麦克风输入，同时叠加了女 士的语音信号（speech2）。此时男子将会听到女士的声音叠加了自己的声音，影响了正常的通话质量。此时在女士所在房间应用回音抵消 模块，可以抵消掉男子的回音，让男子只听到女士的声音。 2． 由于2-4线转换引入的线路回音（见下图）： 在ADSL Modem和交换机上都存在2-4线转换的电路，由于电路存在不匹配的问题，会有一部分的信号被反馈回来，形成了回音。如果在交 换机侧不加回音抵消功能，打电话的人就会自己听到自己的声音。 不管产生的原因如何，对语音通讯终端或者语音中继交换机需要做的事情都一样：在发送时，把不需要的回音从语音流中间去掉。 试想一下，对一个至少混合了两个声音的语音流，要把它们分开，然后去掉其中一个，难度何其之大。就像一瓶蓝墨水和一瓶红墨水倒在 一起，然后需要把红墨水提取出来，这恐怕不可能了。所以回声消除被认为是神秘和难以理解的技术也就不奇怪了。诚然，如果仅仅单独 拿来一段混合了回音的语音信号，要去掉回音也是不可能的（就算是最先进的盲信号分离技术也做不到）。但是，实际上，除了这个混合
    信号，我们是可以得到产生回音的原始信号的，虽然不同于回音信号。 我们看下面的AEC声学回声消除框图(本图片转载)。 Figure Acoustic Echo Cancellation in a voice communication terminal 其中，我们可以得到两个信号：一个是蓝色和红色混合的信号1，也就是实际需要发送的speech和实际不需要的echo混合而成的语音流；另 一个就是虚线的信号2，也就是原始的引起回音的语音。那大家会说，哦，原来回声消除这么简单，直接从混合信号1里面把把这个虚线的 2减掉不就行了？请注意，拿到的这个虚线信号2和回音echo是有差异的，直接相减会使语音面目全非。我们把混合信号1叫做近端信号ne， 虚线信号2叫做远端参考信号fe，如果没有fe这个信号，回声消除就是不可能完成的任务，就像“巧妇难为无米之炊”。 虽然参考信号fe和echo不完全一样，存在差异，但是二者是高度相关的，这也是echo称之为回音的原因。至少，回音的语义和参考信号是 一样的，也还听得懂，但是如果你说一句，马上又听到自己的话回来一句，那是比较难受的。既然fe和echo高度相关，echo又是fe引起 的，我们可以把echo表示为fe的数学函数：echo=F（fe）。函数F被称之为回音路径。在声学回声消除里面，函数F表示声音在墙壁，天花 板等表面多次反射的物理过程；在线路回声消除里面，函数F表示电子线路的二四线匹配耦合过程。很显然，我们下面要做的工作就是求 解函数F。得到函数F就可以从fe计算得到echo，然后从混合信号1里面减掉echo就实现了回声消除。 尽管回声消除是非常复杂的技术，但我们可以简单的描述这种处理方法： 　　1、房间A的音频会议系统接收到房间B中的声音 　　2、声音被采样，这一采样被称为回声消除参考 　　3、随后声音被送到房间A的音箱和声学回声消除器中 　　4、房间B的声音和房间A的声音一起被房间A的话筒拾取 　　5、声音被送到声学回声消除器中，与原始的采样进行比较，移除房间B的声音 求解回音路径函数F的过程恐怕就是比较难以表达的数学公式了。鉴于通俗表达数学公式的难度比发现数学公式还难，笔者就不费力解释 了。下面这段表达了利用自适应滤波器原理求解函数F的过程。（以下可以跳过） 自适应滤波器 自适应滤波器是以输入和输出信号的统计特性的估计为依据，采取特定算法自动地调整滤波器系数，使其达到最佳滤波特性的一种算法或 装置。自适应滤波器可以是连续域的或是离散域的。离散域自适应滤波器由一组抽头延迟线、可变加权系数和自动调整系数的机构组成。 附图表示一个离散域自适应滤波器用于模拟未知离散系统的信号流图。自适应滤波器对输入信号序列x(n)的每一个样值，按特定的算法， 更新、调整加权系数，使输出信号序列y(n)与期望输出信号序列d(n)相比较的均方误差为最小，即输出信号序列y(n)逼近期望信号序列 d(n)。 以最小均方误差为准则设计的自适应滤波器的系数可以由维纳-霍甫夫方程解得。 B.维德罗提出的一种方法，能实时求解自适应滤波器系数，其结果接近维纳－霍甫夫方程近似解。这种算法称为最小均方算法或简称 LMS 法。这一算法利用最陡下降法，由均方误差的梯度估计从现时刻滤波器系数向量迭代计算下一个时刻的系数向量 式中ks为一负数，它的取值决定算法的收敛性， V【ε2(n)】为均方误差梯度估计，
    自适应滤波器应用于通信领域的自动均衡、回声消除、天线阵波束形成，以及其他有关领域信号处理的参数识别、噪声消除、谱估计等方 面。对于不同的应用，只是所加输入信号和期望信号不同，基本原理则是相同的。（以上部分可以跳过） 上面这段话表明，需要求解的回音路径函数F就是一个自适应滤波器W(n)收敛的过程。所加输入信号x(n)是fe，期望信号是echo，自适应滤 波器收敛后的W(n)就是回音路径函数F。 收敛之后，当实际回音发生，我们把fe通过函数W(n)，就可以得到一个很准确的echo，把混合信 号直接减去echo，得到实际需要发送的语音speech，完成回声消除任务。 值得注意的两点： 1、 自适应滤波器收敛阶段，期望信号是完全的echo，不能混杂有speech。因为speech和fe是没有关系的，会扰乱W(n)的收敛过程。 也就是说要求回声消除算法开始运转后收敛要非常快，最好对方还来不及说话，你一说就收敛好了；收敛好之后，如果对方开始说话，也 就是有speech混合过来，这个W(n)系数就不要变化了，需要稳定下来。 2、 回音路径可能是变化的，一旦出现变化，回声消除算法要能判断出来，因为自适应滤波器学习要重新开始，也就是W(n)需要一 个新的收敛过程，以逼近新的回音路径函数F。 基本上来说，上面这两点是两难的，一个需要自适应滤波器收敛后保持系数稳定，以保证不受speech说话干扰，另一个需要自适应滤波器 随时保持更新状态，以保证能够追踪变化的回音路径。这样一来，仅从数学算法层面，回声消除已经是难上加难！简单地说，回声消除自 适应滤波器的设计具有两个互相矛盾的特性，也就是快速收敛和高度的稳定性，如何同时实现这两项特性，正是设计上的主要挑战。 经过上面的分析，相信大家对回声消除的原理和技术有了深刻的理解，这是一门即容易理解又难以实现的技术。 从应用平台来看，根据笔者多年的经验，可以把回声消除分为两大类：基于DSP等实时平台的回声消除技术和基于Windows等非实时平台 的回声消除技术。两者的技术难度和重点是不一样的。 回声消除基本原理是用一个自适应滤波器对未知的回声信道w进行参数辨识，以扬声器信号与产生的多路回声的相关性为基础，建立远 端信号模型，模拟回声路径，通过自适应算法的调整，使其冲激响应与真实回声路径相逼近，从而得到回声预测信号，并不断的修改滤波 器的系数，使得估计值更加逼近真实的回声，然后将预测信号（即估计出来的回声）从麦克风接收到的信号中减去，即可实现回声消除。 用表达式表示如下： echo = x*w d = s + echo y = x * w e = d - y 对于理想的回声消除器，e为近端说话人的语音信号s 来源：面向实时通信系统的自适应回声消除算法研究_文昊翔文昊翔 来源：面向实时通信系统的自适应回声消除算法研究 回声系统的冲激响应序列可简称为回声路径，假设回声路径为时不变或者缓变 回声以延时为主，表现在回声路径则为稀疏性，即回声路径大部分系数幅值为零值或极小值以模拟回声延时。回声路径 真正产生回声能量的大幅值班系数，称为活跃系数，活跃系数在时域聚集，数量只占回声路径系数总量极少一部分。 利用回声路径的稀疏性，最直接的方式，是先用一个自适应滤波器对回声路径进行粗略的延时估计，再另外用一个短的 自适应滤波器精确辨识回声路径的活跃系数，以提高收敛速度，减少计算复杂度。以延时估计为基础的双滤波器结构已 经在飞思卡尔半导体公司的回声消除器上获得成功应用 例，当回声消除器可处理128ms延时时，在8kHz采样频率条件下，自适应滤波器需要1024个系数 NLMS算法的主要缺点是当输入信号为有色噪声时，算法收敛速度将减慢。为提高EC系统抗有色噪声能力，进一步提高 算法收敛速度。Ozeki与Umeda提出仿射投影算法（Affine Projection Algorithm,APA）。AP通过为系统引入记忆性，重复利用
    数据加快算法收敛。APA是NLMS的高阶形式，当APA阶数降为1时可得NLMS算法。 LMS、NLMS、APA均为随机梯度算法，随机梯度算法需要引入收敛步长u。初期的变步长算法由Gitlin提出，其步长幅值 随迭代次数增加而减小，当步长减小后，目标系统出现突变时，算法的跟踪能力极差。Paleologu等提出无参数变步长 NLMS算法， 自适应算法的分析，推导过程均基于独立性假设，即系统不同时刻的输入信号彼此相互统计独立，在EC应用，任一系统 输入的语音信号具有强相关性，非平稳性等特征，明显偏离独立性假设，严重时甚至使算法无法收敛。为提高自适应算 法工作于强相关信号输入时的收敛速度，有各种解相关算法提出。早期的解相关算法多为频域解相关（Dentino较早提出 频域解相关的概念），但时频转换计算复杂度高，因此在时域进行解相关是一种更优的选择。解相关算法的核心是先对 输入信号进行预处理，将输入信号向量X(k)分解为与X(k-1)平行的Xp(k)分量及与X(k-1）正交的Z(k)分量，然后用Z(k)分量 更新滤波器系数，以满足独立性假设。 Proportionate算法（算法（P算法算法)通过为滤波顺务系数赋予不同的收敛步长以提高算法收敛速度 通过引用P步长加快算法收敛速度。 通过为滤波顺务系数赋予不同的收敛步长以提高算法收敛速度 。P算法以NLMS为基础， 子带滤波以数学信号的抽样与插值为基础， M抽样与们号输入的关系为： M插值信号与输出的关系为： LMS、NLMS、APA算法物理意义是滤波器系数在均方误差曲面沿最陡梯度方向下降至其最优值，因此被称为最陡梯度下 降算法。与最陡梯度下降算法相比，递归最小二乘（RLS）算法是一种收敛速度更快的算法。直接求解RLS算法计算复杂 度过大，快速RLS算法可有效降低计算复杂度，但无法保证系统稳定性。因此RLS算法目前尚无法应用于EC系统 与FIR自适应算法相比，IIR自适应算法的优点是大幅减小滤波器长度。但其缺点也非常明显： 一、每次滤波器系数更新后，都要进行IIR滤波器极点的稳定性判段，这需要进行因式分解，计算复杂度巨大 二、IIR滤波器的MSE曲面与滤波器系数向量并非成二次函数关系，即MSE曲面存在多个局部极小值点，极小值点数不仅 与自适应系统、目标系统阶数相关，而且与输入信号特性有关 三、IIR滤波器无法保证严格的线性相位特性，而语音信号对相位特性有严格要求。因此IIR自适应算法在实际应用时极难 操作。 双端发声检测是指通信过程中，远端用户与近端用户同时说话的现象，此时远端语音产生的回声信号被大功率的近端语音信号淹没，因近 端语音信号与远端语音信号相互独立，若此时滤波器系数继续进行自适应更新，将导致算法发散。双端发声现象在通信中频繁发生，概率 约为20%。针对双端发声现象，最常用的方法是在EC系统设置一个双端发声检测器，当检测到双端发声时，停止自适应算法，当双端发声 停止后，自适应算法继续进行 5延时估计算法与部分系数更新算法 延时估计算法与部分系数更新算法 P算法利用回声路径的稀疏性加快自适应算法的收敛速度。但其收敛速度的提高以计算复杂度的增加为代价，过高的计算复杂度与EC系统 的实时性要求形成尖锐的矛盾，与P算法相比，延时估计（Delay Estimate，DE）算法更有效地利用回声路径的稀疏性。利用回声路径活跃 系数只占全部系数极小一部分，且在时域上集中的特性，DE算法先对回声延时进行检测，然后对滤波器的期望信号进行相应的延时，以一 个短的滤波器辨识回声路径的活跃系数，从根本上解决滤波器过长导致的各种问题。 部分系数更新算法（Selective Partial Updates,SPU）每次迭代只更新一部分量重要的系数以减小算法的计算复杂度。系数重要性的判断准则 为SPU算法的核心，Dogancay提出按输入信号幅值排序确定对应滤波器系数的重要性，Hongyan提出结合回声路径的稀疏性，对滤波器进 行分段卷积，对卷积结果进行排序以确定系数的重要性。
    在实际应用中，DE、SPU算法仍然存在各种缺陷。DE算法的双滤波器结构导致信息冗余，浪费计算复杂度；SPU算法因未能更新全部活跃 系数导致算法性能下降。此外，DE、SPU算法稳定性均不满足应用要求。 结合SPU与DE算法，提出Delay-SPU算法。D-SPU对滤波器系数幅值进行移动窗积分，以积分值对应部分为活跃系数，每次迭代均更新活跃 系数与循环更新一段非活跃系数。更新活跃系数可使算法精确辨识回声路径，循环更新一段非活跃系数以确保算法具备跟踪能力。D-SPU 仅用一个滤波器进行延时估计与活跃系数更新，避免双滤波器结构的信息冗余；只更新部分滤波器系数，以减小滤波器的有效长度。因此 D-SPU算法复杂度低，收敛速度快，有较强的实际应用价值。 5.1延时估计算法 延时估计算法 5.1.1延时估计算法原理 延时估计算法原理 根据ITU-T G.168标准，电子回声L值小于12ms，典型值约为4ms。声学回声L值大于电子回声L值，在传统EC算法中。D定义为活跃系数峰 值的横坐标位置，更严格的定义为： D的不同定义并不影响DE算法和稳定性。因DE算法只需要对D进行粗略估计，通过适当增加滤波器的长度，仍可保证滤湨器精确辨识回声 路径的活跃系数。但获得更换精确的D，可减小滤波器有效长度，改善算法性能。 5.1.2 Haar子带变换延时估计算法 子带变换延时估计算法 对输入信号进行时频变换，在频域对变换信号进行自适应滤波，可有效解除输入信号的相关性。相关算法被称为频域自适应算法。传统的 时频变换如Hartley、DCT变换与FFT变换相似，均存在频域信息局部化而时域信息完全丢失的缺点。因此无法应用于延时估计。 5.2部分系数更新算法 5.2.1输入信号幅值班排序SPU算法 SPU算法在每次迭代时，只更新滤波器的部分系数，以降低算法的复杂度。早期的SPU算法仅是简单地将滤波器分段，每次迭代时随机或 循环更新其中一段系数。因未能对需要更新的系数进行优化选择，导致算法性能下降极为严重。Dogancay提出对输入信号按幅值进行排 序，仅更新最大幅值输入信号对应的滤波器系数，称为Max-SPU算法。推导过程如下： 分段块频域自适应滤波算法 主要思想：将自适应滤波器的系数w分成相等的长度，然后将其变换到频域，这样将得到混合的时域和频域 分段块频域自适应滤波算法 自适应滤波，即所谓的分段块频域自适应滤波，对于此算法的一次迭代，分为如下几个步骤： （1）对参考信号分段并做FFT变换 （2）分别对各段数据做频域滤波，累加后作FFT反变换，并只取后L点为有效的线性卷积结果，得到的是估计信号 （3）将估计信号从回声信号中去除，得到的是残差信号 （4）计算子带步长 （5）调整各段滤波器系数 论文首先总结目前LMS算法的主要发展方向，然后从LMS算法的迭代步长以及滤波器的阶数选择两个方面， 最小均方算法，简称LMS算法，是Widrow和Hoff在1959年研究自适应线性元素的模式识别方案时提出的，因为LMS算法具有计算复杂度 低，在平稳环境中的收敛性好，其均值班无偏地收敛到维纳解，性能稳定，结构简单，使LMS算法成为自适应算法中应用最广泛的算法， 一个典型的LMS算法的描述如下： 经典的LMS算法的缺点是收敛速度慢，许多方面的研究，旨在提高LMS的收敛速度，提升LMS算法的收敛性能，因此新的LMS算法不断出 现。 步长在LMS算法迭代过程中是一个矛盾量，它既控制着LMS算法的收敛速度，同时决定着算法的稳态误差，人们提出了许多变频长LMS算 法，即在算法收敛过程中动态调整步长的大小，这些算法的根本思想是在算法开始阶段采用较大的步长，使算法具有较快的收敛速度和跟 踪速度，随着收敛的加深逐渐减小步长使算法有较小的稳态误差。 LMS算法是在维纳滤波的基础上，借鉴最速下降算法的思想而发展起来的。 衡量LMS算法性能的指标主要有算法的收敛性、收敛速度、稳态误差及计算复杂度。 稳态误差是指算法进入稳态后滤波器权值距离最优解之间的远近。
    在LMS算法收敛过程中，影响其性能的参数主要有迭代步长 迭代步长 ，滤波器阶数 滤波器阶数 和滤波器权值的初始值 滤波器权值的初始值 。 很多人对步长参数在收敛速度和稳太误差的矛盾这个问题了做了大量的研究，提出了一系列变步长的改进LMS算法，主要思想是在算法收 敛阶段使用较大的步长参数以提高收敛速度，而在算法收敛后采用小步长以减小稳态误差，变步长的LMS算法很好的解决了步长参数在算 法收敛速度与稳态误差之间的矛盾。 滤波器的阶数也是滤波器设计过程中很重要的一个参数，当滤波器的阶数选择过小，我们称之为欠滤波器长度，则必将带来较大的误差， 可能会导致LMS算法发散。 对于相同的输入情况、收敛因子和滤波器阶数，权矢量初始值实际上决定了收敛过程的路程。初始值距离维纳解越近，权矢量的收敛时间 越短。然而，权矢量的收敛过程终点的维纳解由输入信号及期望信号的先验统计信息决定，这在实际中是不可能获得的，因此在进行LMS 算法研究时，大都假定为零初始值。 失调与滤波器输入的能量成正比，因此当输入信号能量较大时，LMS滤波器遇到梯度噪声放大问题。为了克服这一因难，可采用归一化 LMS滤波器。 变步长两个方向： 变步长两个方向： （1）利用误差信号迭代步长 （2）利用梯度向量进行步长迭代 利用误差信号进行步长迭代的典型变步长LMS算法，其中以Kwong算法为代表，Aboulnasr算法和Pazaitis算法对Kwong算法做了改进 另一类变步长LMS算法是利用梯度向量来迭代步长，这类方法利用了梯度向量的两个特点： （1）梯度向量的模初始阶段较大，稳态时较小且趋于零 （2）梯度的方向在初始阶段较为一致，到系统收敛后变化较频繁 梯度向量的这两个特点很好的满足了迭代步长的变化要求，典型的算法有Karni算法和Mathew算法 （其实梯度就是滤波器权系数沿误差性能曲面的斜率 其实梯度就是滤波器权系数沿误差性能曲面的斜率 ） 回声消除器用于确定声学信道的传递函数，也就是扬声器和麦克风之间的冲击响应w(n)，它通常是指有限冲击响应滤波器，通过w(n)和 x(n)的卷积得到复制回声y(n)，误差是实际回声d(n)与复制回声y(n)的差，即： e(n)=d(n)-y(n)，其中d(n)=w(n)*x(n)+t(n)，这里t(n)表示环境噪声。 NLMS算法以其简单性和稳定性，被广泛应用于商业回声消除器中，然而，LMS和NLMS算法的主要缺点是收敛速度慢 变阶数变阶数LMS算法分析 算法分析 在进行滤波器设计的时候，滤波器的阶数通常是未知的（虽然通常会假定一个已知的固定值），阶数如果选取的过小，将会给滤波器的设 计带来较大的误差，如果阶数选取的过大，不但会带来较大的计算量，同时也会导致算法的误差。 三种经典的变阶数LMS算法： （1）分割波滤器LMS算法 （2）梯度下降LMS算法 （3）分数阶数LMS算法 上一次分享了回声消除算法的基本原理，自然提出一个问题，如何才能快速收敛的问题，主要是两个问题，一个是最优 步长的选择，第二个是滤波器的阶数的选择，这次只关注第一个问题：
    这里V(n)在别的地方也有叫失调的
    由于变步长LMS算法要求步长因子u(n)在自适应初始阶段较大以保证算法有较快的收敛速度，而算法收敛后则很小很小的稳态误差，因 些，步长因子和自适应滤波器输出之间存在着非线性关系。若将步长因子与输出误差之间的关系近似为S（Sigmoid）函数，就形成了基于 S函数的变步长自适应LMS算法 在基本的LMS算法中，当步长一定时，自适应滤波器的收敛速度取决于输入序列自相关矩阵R的最小特征值，而总失调量主要取决于最小 特征值中的最大值。由于R的特征值随输入信号改变，这将影响LMS算法的收敛速度和失调
    分享到：
    赞 收藏

    相关推荐

    资料库

    音视频

    共收录313份资料，累计4个分类，关注成员有19位，主要包括：图像识别,直播技术,编解码,图像处理

    热门标签

    图像识别 直播技术 编解码 图像处理

    最新资料