第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
算法与数据结构课程设计报告B-trees的实现及分析.doc
算 法 与 数 据 结 构
课 程 设 计 报 告
班
学
题
目: B-Trees 的实现及分析
级:
号:
名:
姓
指导教师:
绩:
成
2012 年 1 月 6 日
一、题目
(1) 问题描述
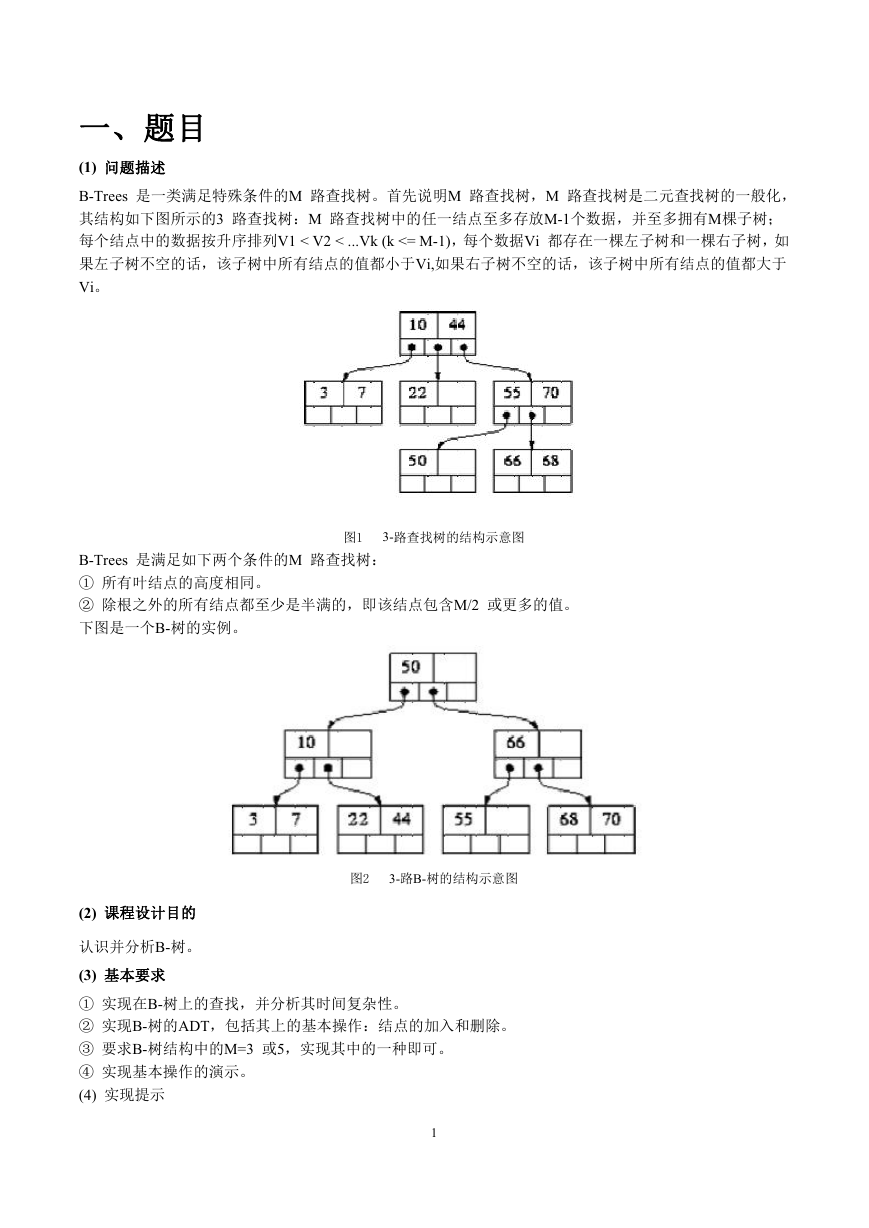
B-Trees 是一类满足特殊条件的M 路查找树。首先说明M 路查找树，M 路查找树是二元查找树的一般化，
其结构如下图所示的3 路查找树：M 路查找树中的任一结点至多存放M-1个数据，并至多拥有M棵子树；
每个结点中的数据按升序排列V1 < V2 < ...Vk (k <= M-1)，每个数据Vi 都存在一棵左子树和一棵右子树，如
果左子树不空的话，该子树中所有结点的值都小于Vi,如果右子树不空的话，该子树中所有结点的值都大于
Vi。
图1
3-路查找树的结构示意图
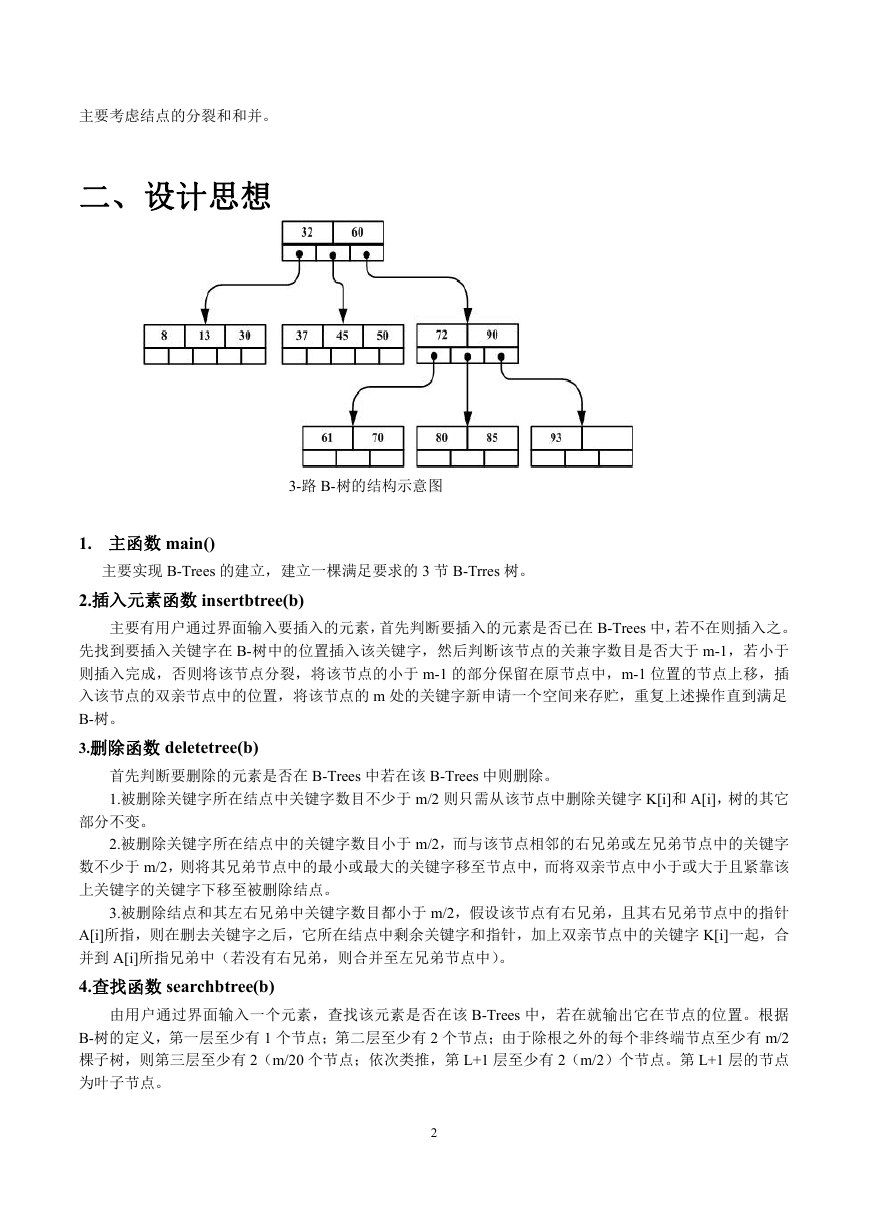
B-Trees 是满足如下两个条件的M 路查找树：
① 所有叶结点的高度相同。
② 除根之外的所有结点都至少是半满的，即该结点包含M/2 或更多的值。
下图是一个B-树的实例。
图2
3-路B-树的结构示意图
(2) 课程设计目的
认识并分析B-树。
(3) 基本要求
① 实现在B-树上的查找，并分析其时间复杂性。
② 实现B-树的ADT，包括其上的基本操作：结点的加入和删除。
③ 要求B-树结构中的M=3 或5，实现其中的一种即可。
④ 实现基本操作的演示。
(4) 实现提示
1
主要考虑结点的分裂和和并。
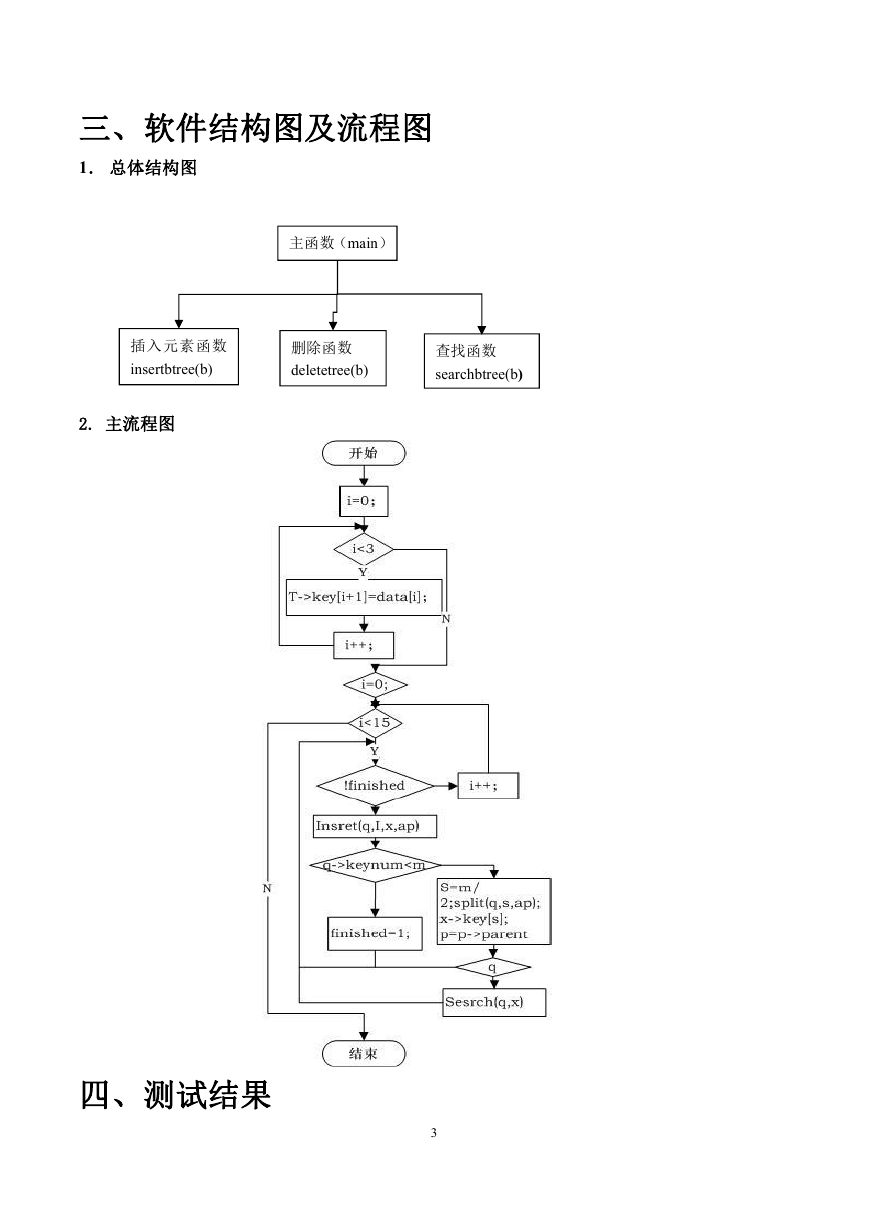
二、设计思想
3-路 B-树的结构示意图
1. 主函数 main()
主要实现 B-Trees 的建立，建立一棵满足要求的 3 节 B-Trres 树。
2.插入元素函数 insertbtree(b)
主要有用户通过界面输入要插入的元素，首先判断要插入的元素是否已在 B-Trees 中，若不在则插入之。
先找到要插入关键字在 B-树中的位置插入该关键字，然后判断该节点的关兼字数目是否大于 m-1，若小于
则插入完成，否则将该节点分裂，将该节点的小于 m-1 的部分保留在原节点中，m-1 位置的节点上移，插
入该节点的双亲节点中的位置，将该节点的 m 处的关键字新申请一个空间来存贮，重复上述操作直到满足
B-树。
3.删除函数 deletetree(b)
首先判断要删除的元素是否在 B-Trees 中若在该 B-Trees 中则删除。
1.被删除关键字所在结点中关键字数目不少于 m/2 则只需从该节点中删除关键字 K[i]和 A[i]，树的其它
部分不变。
2.被删除关键字所在结点中的关键字数目小于 m/2，而与该节点相邻的右兄弟或左兄弟节点中的关键字
数不少于 m/2，则将其兄弟节点中的最小或最大的关键字移至节点中，而将双亲节点中小于或大于且紧靠该
上关键字的关键字下移至被删除结点。
3.被删除结点和其左右兄弟中关键字数目都小于 m/2，假设该节点有右兄弟，且其右兄弟节点中的指针
A[i]所指，则在删去关键字之后，它所在结点中剩余关键字和指针，加上双亲节点中的关键字 K[i]一起，合
并到 A[i]所指兄弟中（若没有右兄弟，则合并至左兄弟节点中）。
4.查找函数 searchbtree(b)
由用户通过界面输入一个元素，查找该元素是否在该 B-Trees 中，若在就输出它在节点的位置。根据
B-树的定义，第一层至少有 1 个节点；第二层至少有 2 个节点；由于除根之外的每个非终端节点至少有 m/2
棵子树，则第三层至少有 2（m/20 个节点；依次类推，第 L+1 层至少有 2（m/2）个节点。第 L+1 层的节点
为叶子节点。
2
三、软件结构图及流程图
1． 总体结构图
主函数（main）
插入元素函数
insertbtree(b)
删除函数
deletetree(b)
查找函数
searchbtree(b)
2. 主流程图
四、测试结果
3
1.查询结点
（元素存在时，能找到元素的位置）
2.插入结点
（元素不存在时，在不到该元素）
（元素不存在时，插入成功）
（元素存在时，插入失败）
4
3. 删除结点
（元素存在时，删除成功）
（元素不存在时，无法删除）
五、分析与探讨
1. 测试结果分析
1.关键字集合分布在整颗树中；
2.任何一个关键字出现且只出现在一个结点中；
3.搜索有可能在非叶子结点结束；
4.其搜索性能等价于在关键字全集内做一次二分查找；
5.自动层次控制；由于限制了除根结点以外的非叶子结点，至少含有 M/2 个儿子，确保了结点的至少利用
率，其最底搜索性能为：其中，M 为设定的非叶子结点最多子树个数，N 为关键字总数；所以 B-树的性能总
是等价于二分查找（与 M 值无关），也就没有 B 树平衡的问题；由于 M/2 的限制，在插入结点时，如果结点
已满，需要将结点分裂为两个各占 M/2 的结点；删除结点时，需将两个不足 M/2 的兄弟节点合并.
复杂度分析：
插入的时间复杂度：Einsert=∑pi*(n-i+1) =n/2（其中 Pi=1/(n+1)）O（n）
删除的时间复杂度：Edelete=∑pi*(n-i) =(n-1)/2 。（其中 Pi=1/n）O（n）
插入的时空复杂度：S（n）
插入的时空复杂度：S（n）
2. 探讨：
M=3 的 B-树 B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结
5
束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点。
每个结点存放至少 M/2-1（取上整）和至多 M-1 个关键字；（至少 2 个关键字,根节点至少一个关键
字）；非叶子结点的指针：P[1], P[2], …, P[M]；其中 P[1]指向关键字小于 K[1]的子树，P[M]指
向关键字大于 K[M-1]的子树，其它 P 指向关键字属于(K[i-1], K)的子树。
附录：源代码（6 号字体，2 栏排版）
#include
#include
#include
#define m 4
#define max 32767
typedef struct BTNode
{
//B-Trees 为 4 阶
else
{
printf("\n\t 找不到这个元素！！！\n");}
printf("\n\t 该元素为第%d 结点！！！",i);
//结点的大小
int keynum;
struct BTNode *parent;
int key[m+1];
struct BTNode *ptr[m+1];
//双亲指针
//关键字向量
//子树指针向量
//B-Trees 的节点结构
}BTNode,*BTree;
int data[15]={8,30,45,32,60,80,50,61,70,85,13,37,72,90,93};// 定 义
B-Trees 序列数
BTree T,R,R1;
int rag;
void search(BTree p2,int a)//查找
{
int j;
for(j=1;jkey[j]>a)
break;
rag=j-1;
}
BTree searchtree(int k) //查找插入元素的位置
{
int j;
BTree p1,q1;
p1=T;
while(p1)
{
for(j=1;jkey[j]>k)
break;
q1=p1;
p1=p1->ptr[j-1];
}
rag=j-1;
return q1;
}
int searchbtree(int k,int h)
{
//查询，判断元素是否存在
int i,found=0;
BTree p;
p=T;
while((!found)&&(p->ptr[0]!=NULL))
{
for(i=1;ikey[i])
break;
if(p->key[i]==k)
found=1;
else
p=p->ptr[i-1];
}
if(p->ptr[0]==NULL)
for(i=1;ikey[i])
break;
if(p->key[i]==k)
found=1;
if(h==1){
if(found==0){
}
}
return found;
}
void insertbtree(int x) //插入元素
{
int j,finished,s;
BTree q,p;
finished=0;
q=searchtree(x); //调用 searchtree()函数查找要插入元素的位置
while(!finished)
{
if(q->keynum==0)//当要插入的元素为新申请的根结点
{
q->ptr[0]=p;q->ptr[1]=R;q->key[1]=x;
q->keynum++;p->parent=q;R->parent=q;
}
else if((q->keynum!=0)&&(q->ptr[0]!=NULL))//当要插入的元素是
中间的结点
{
}
else
{
q->key[j+1]=q->key[j];
q->ptr[j+1]=q->ptr[j];
for(j=3;j>rag;j--)
{
}
q->ptr[j+1]=R;
R->parent=q;
q->key[j+1]=x;
q->keynum++;
//当插入的元素是最下层的结点时
q->key[j+1]=q->key[j];
for(j=3;j>rag;j--)
q->key[j+1]=x;
q->keynum++;
}
finished=0;
if(q->keynumkey[s];q->key[s]=max;q->keynum=s-1;
R=(BTNode*)malloc(sizeof(BTNode)); // 新 申 请 一 个 结点
来存放分裂的另一部分数据
R->key[1]=q->key[s+1];
for(j=2;j<=m;j++)
{
R->key[j]=max;R->ptr[j]=NULL;
}
R->ptr[0]=q->ptr[s];R->ptr[1]=q->ptr[s+1];
R->keynum=1;q->key[s+1]=max;p=q;q=q->parent;
if(!q)
{
R1=(BTNode*)malloc(sizeof(BTNode));
// 新
6
int i,h;
BTree p,q0,q1;
p=q->parent;
for(h=0;hptr[h]==q)
break;
q1=p->ptr[h+1];
if(h==0)
else
{
}
if(q->keynum>=m/2)
for(i=j;iptr[h-1];q1=p->ptr[h+1];
//当节点的数目不小于 m/2
q->key[i]=q->key[i+1];
else if((q->keynumkeynum>=2||q1->keynum>=2))
//当结点的数目少于 m/2 但其左兄弟或右兄弟的结点数目大于时
{
if(q1->keynum>=m/2)
{
//右兄弟时
q->key[j]=p->key[h];p->key[h]=q1->key[0];
for(i=0;ikey[i]=q1->key[i+1];
q1->keynum--;
}
else
{
//左兄弟时
q->key[j]=p->key[h];p->key[h]=q0->key[q0->keynum];
q0->key[q0->keynum]=q0->key[q0->keynum+1];q0->keynum--;
}
}
else
//当结点的数目少于 m/2 且其左兄弟和右兄弟的结
点数目小于时
{
if(h==0)
{
//当该节点只有有兄弟时
位置
q->key[1]=p->key[1];q->key[2]=q1->key[1];q->keynum=2;free(q
int i,found=0;
BTree p;
p=T;
while((!found)&&(p->ptr[0]!=NULL)) //找到要插入节点的位置
{
//找到要插入节点的位置
//当要删除元素是终端结点
deletetree2(p,i);
//当插入节点不是终端结点
int x,i,finished,s,j;
BTree q,p;
T=(BTNode*)malloc(sizeof(BTNode));T->keynum=0;
for(i=0;i<3;i++)
{
T->key[i+1]=data[i];T->keynum++;
for(i=1;ikey[i])
break;
if(p->key[i]==k)
found=1;
else
p=p->ptr[i-1];
}
if(p->ptr[0]==NULL)
for(i=1;ikey[i])
break;
if(p->ptr[0]==NULL)
deletetree1(p,i);
else
}
void main()
{
}
T->key[4]=max;
for(i=0;i<5;i++)
T->ptr[i]=NULL;
T->parent=NULL;
for(i=3;i<15;i++)
{
while(!finished)
{
根节点,且为新申请的根结点
{
申请一个节点作为根节点
}
else
}
}
}
T=q=R1; q->keynum=0;q->parent=NULL;
for(j=1;j<=m;j++)
q->key[j]=max;
for(j=0;j<=m;j++)
q->ptr[j]=NULL;
search(q,x); //查找要插入元素的位置
{
}
BTree p;
p=q;
while(q->ptr[0])//找终端结点
{
q=q->ptr[j];
if(q->ptr[0]!=NULL)
q=q->ptr[0];
}
q=q->parent;p->key[j]=q->key[1];
deletetree1(q,1);
void deletetree1(BTree q,int j) //当要删除的节点是终端结点,j 是要删除
元素是节点的地几个元素
{
void deletetree(int k)
{
1);
0);
}
x=data[i];finished=0;q=searchtree(x); //查找要插入元素的
if(q->keynum==0)
//当要插入的元素所在结点是
for(i=1;ikeynum--;
p->key[i]=p->key[i+1];p->key[i]=p->key[i+1];
q->ptr[0]=p;q->ptr[1]=R;
}
else
{
//当该节点有左兄弟时
q->key[1]=x;q->keynum++;p->parent=q;R->parent=q;
}
else if((q->keynum!=0)&&(q->ptr[0]!=NULL))
// 当
要插入的元素所在结点是中间的结点
q->key[1]=p->key[h];q->key[2]=q0->key[1];q->keynum=2;free(q
{
for(i=1;ikeynum--;
p->key[i]=p->key[i+1];
p->ptr[i]=p->ptr[i+1];
}
}
void deletetree2(BTree q,int j) //要插入节点是非终端结点
for(j=3;j>rag;j--)
{q->key[j+1]=q->key[j];q->ptr[j+1]=q->ptr[j];}
q->ptr[j+1]=R;R->parent=q;q->key[j+1]=x;q->keynum++;
//当插入的元素所在结点是最下层的结点
for(j=3;j>rag;j--)
q->key[j+1]=q->key[j];
q->key[j+1]=x;q->keynum++;
}
else
时
{
7
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
