离散数学的应用 Chan_Keyword 1 离散数学简介 离散数学（Discrete mathematics）是研究离散量的结构及其相互关系的数学 学科，是现代数学的一个重要分支。离散的含义是指不同的连接在一起的元素， 主要是研究基于离散量的结构和相互间的关系，其对象一般是有限个或可数个元 素。离散数学也叫组合数学，广义的组合数学就是离散数学，总之，组合数学是 一门研究离散对象的科学。随着计算机科学的日益发展，组合数学的重要性也日 渐凸显，因为计算机科学的核心内容是使用算法处理离散数据。狭义的组合数学 主要研究满足一定条件的组态（也称组合模型）的存在、计数以及构造等方面的 问题。 组合数学的主要内容有组合计数、组合设计、组合矩阵、组合优化（最 佳组合）等。 离散数学内容主要分为四大部分，分别是数理逻辑、集合论、代数结构和图 论。每个阶段内容都有深浅，在本科教学过程中，一般都讲解各部分的基础知识， 按各部分内容深浅由如下划分： 内容 基础知识 扩展知识 前沿研究 实践应用 数理逻辑 集合论 代数结构 图论 命题逻辑、谓 词逻辑和推理 理论等 集合、关系和 函数等 代数、半群、 群、环、域等 图、路径、回 路、树等 逻辑运算、位 运算 形式逻辑、智 能算法 搜索引 擎、硬件设计 容斥、序列 运筹、密码 最优调度、软 件测试、公钥 加密算法 置换群、李群 近世代数 匹配、着色、 支撑、覆盖 图论应用 指令优化、路 径寻优 离散数学的知识内容及应用领域可用图 1.1 来概括。 离散数学 离散数学 数理逻辑 集合与关系 代数系统 图论 网 络 协 议 分 析 网 络 安 全 计 算 机 组 成 与 结 构 数 据 库 原 理 编 译 原 理 现 代 密 码 学 数 据 结 构 软 件 工 程 图 1.1 离散数学各部分的应用 信 息 论 与 编 码 数 字 水 印 隐 写 与 隐 写 分 析 

2 离散数学在数据结构中的应用 数据结构中将操作对象间的关系分为四类：集合、线性结构、树形结构、图 状结构或网状结构。数据结构研究的主要内容是数据的逻辑结构，物理存储结构 以及基本运算操作。其中逻辑结构和基本运算操作来源于离散数学中的离散结构 和算法思考。离散数学中的集合论、关系、图论、树四个章节就反映了数据结构 中四大结构的知识。如集合由元素组成，元素可理解为世上的客观事物。关系是 集合的元素之间都存在某种关系。例如雇员与其工资之间的关系。图论是有许多 现代应用的古老题目。还可以用边上带权值的图来解决诸如寻找交通网络里两城 市之间最短通路的问题。而树反映对象之间的关系，如组织机构图、家族图、二 进制编码都是以树作为模型来讨论，常用的操作系统中用于文件索引和磁盘读写 的算法就是用的 B 树来进行文件查找，磁盘的根目录及子目录就构成一棵树。 3 离散数学在数据库中的应用 数据库技术被广泛应用于社会各个领域，关系数据库已经成为数据库的主流， 离散数学中的笛卡儿积是一个纯数学理论，是研究关系数据库的一种重要方法， 显示出不可替代的作用。不仅为其提供理论和方法上的支持，更重要的是推动了 数据库技术的研究和发展。 数据库主要就是对各种数据信息进行处理，数据之间存在各种关系。比如一 个学生信息数据库，“学生”与“姓名”之间是所属关系，“姓名”与“学号”是 并列关系等。在管理较庞大和复杂的数据库时，各种数据之间可能存在不止一种 关系，所以离散数学中的对集合关系的研究就起到了重要作用。 关系数据模型建立在严格的集合代数的基础上，其数据的逻辑结构是一个由 行和列组成的二维表来描述关系数据模型。在研究实体集中的域和域之间的可能 关系、表结构的确定与设计、关系操作的数据查询和维护功能的实现、关系分解 的无损连接性分析、连接依赖等问题都用到二元关系理论。 4 离散数学在编译原理中的应用 编译程序是计算机的一个十分复杂的系统程序。编译程序对程序的编译就好 比对一个汉语句子进行翻译，找出“主语”、“谓语”和“宾语”等，对句子结构 进行分析从而理解其表达的意思。对不同的语言进行编译就好像对不同国家的语 言进行分析一样。由此可知，对语言的编译建立在语言本身所依赖的规则之上， 不同的语言有不同的语法规则。一个典型的编译程序一般都含有八个部分：词法 分析程序、语法分析程序、语义分析程序、中间代码生成程序、代码优化程序、 目标代码生成程序、错误检查和处理程序、各种信息表格的管理程序。离散数学 里的计算模型章节里就讲了三种类型的计算模型：文法、有限状态机和图灵机。 具体知识有语言和文法、带输出的有限状态机、不带输出的有限状态机、语言的 识别、图灵机等。短语结构文法根据产生式类型来分类：0 型文法、1 型文法、 2 型文法、3 型文法。以上这些在离散数学里讲述到的知识点在编译原理的词法 分析及语法分析中都会用到。所以离散数学的学习有助于对计算机程序编译原理 

的理解。 5 离散数学在人工智能中的应用 目前，人工智能发展迅速，已成为各国重点研究领域。事实上，人工智能有 很大部分依赖于离散数学。比如最为人们所知的深度学习，神经网络算法，实际 上神经网络就是一个“有向图”，有“边权”、“节点值”，对于简单的网络，只是 在“节点处”加了“激活函数”。 在人工智能的研究与应用领域中，逻辑推理是人工智能研究中最持久的子领 域之一。逻辑是所有数学推理的基础，对人工智能有实际的应用。采用谓词逻辑 语言的演绎过程的形式化有助于我们更清楚地理解推理的某些子命题。逻辑规则 给出数学语句的准确定义。许多非形式的工作，包括医疗诊断和信息检索都可以 和定理证明问题一样加以形式化。因此，在人工智能方法的研究中定理证明是一 个极其重要的论题。在这里，推理机就是实现(机器)推理的程序。它既包括通常 的逻辑推理，也包括基于产生式的操作。推理机是使用知识库中的知识进行推理 而解决问题的。所以推理机也就是专家的思维机制，即专家分析问题、解决问题 的方法的一种算法表示和机器实现。当然以上说的是专家系统，一般来说这种人 工智能已经被基于统计学习的机器学习所取代。 另一方面，在人工智能领域有些研究并未得到严格的数学理论证明，即技术 走在了理论前面。这是因为很多搞计算机的对数学理解不够到位，搞数学的对计 算机理论理解不到位，所以对于计算机专业的尤其是打算学习人工智能方面知识 的学生来说，学好数学显得极其重要。 6 离散数学在通信中的应用 代数系统在计算机中的应用广泛,例如有限机,开关线路的计数等方面。但最 常用的是在纠错码方面的应用。在计算机和数据通信中,经常需要将二进制数字 信号进行传递,这种传递常常距离很远,所以难免会出现错误。通常采用纠错码来 避免这种错误的发生,而设计的这种纠错码的数学基础就是代数系统。纠错码中 的一致校验矩阵就是根据代数系统中的群概念来进行设计的,另外在群码的校正 中,也用到了代数系统中的陪集。在信息编码中，常用的哈夫曼（Haffman）编码 技术，可以有效降低存储空间，对数据进行压缩，从而提高传输效率。其理论原 理是 Haffman 树，一种带权路径长度的二叉树。 7 离散数学在生活中的应用 离散数学在我们日常所见的生活中也有很大的应用，例如物流管理调度，送 货问题等，都需要用到图论相关的算法来规划最短路径或者最优路径，使得收益 最大。我们来看一个简单的例子。现有一个邮递员，要从 A 点开始送信，要求经 过每一街道并回到起始点，求所走的最短路径。假如街道是图 7-1 所示。 

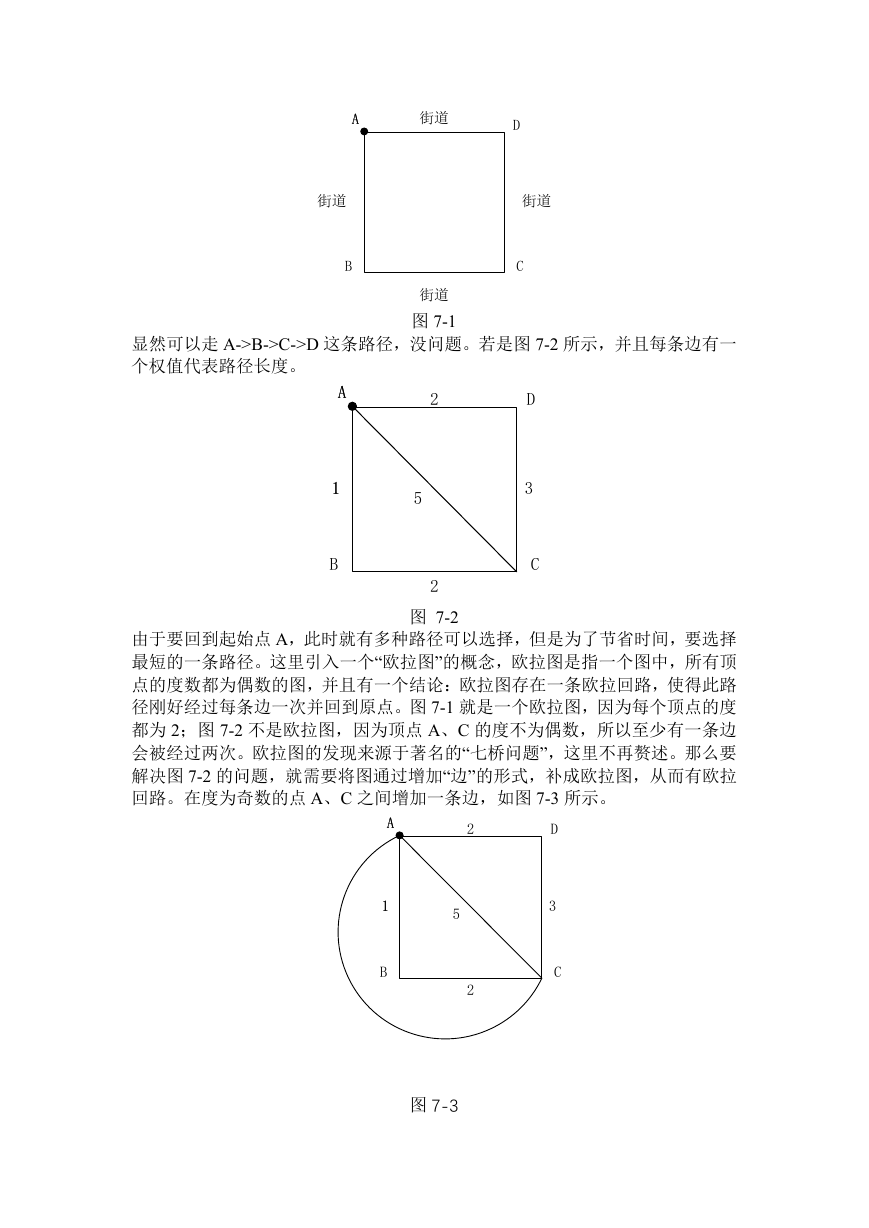
AA 街道 D 街道 B 街道 图 7-1 显然可以走 A->B->C->D 这条路径，没问题。若是图 7-2 所示，并且每条边有一 个权值代表路径长度。 街道 C D 3 C AA 1 1 B 2 2 5 图 7-2 AA 1 1 B 2 2 5 图 7-3 D 3 C 由于要回到起始点 A，此时就有多种路径可以选择，但是为了节省时间，要选择 最短的一条路径。这里引入一个“欧拉图”的概念，欧拉图是指一个图中，所有顶 点的度数都为偶数的图，并且有一个结论：欧拉图存在一条欧拉回路，使得此路 径刚好经过每条边一次并回到原点。图 7-1 就是一个欧拉图，因为每个顶点的度 都为 2；图 7-2 不是欧拉图，因为顶点 A、C 的度不为偶数，所以至少有一条边 会被经过两次。欧拉图的发现来源于著名的“七桥问题”，这里不再赘述。那么要 解决图 7-2 的问题，就需要将图通过增加“边”的形式，补成欧拉图，从而有欧拉 回路。在度为奇数的点 A、C 之间增加一条边，如图 7-3 所示。 

对于增加的这条边的边权值可以是 1+2=3、5、2+3=5.所以选择最小的那个，即 1+2,即选择 A-B-C 这条路径重复走两次，从而使得总路程最短，最短为所有路径 长度加上增加的这条路径的长度。这里就体现了利用图论知识解决现实问题，也 体现了离散数学的魅力。 8 结语 离散数学在计算机理论科学研究中扮演者重要的角色，现实世界中问题的求 解建立在高度的抽象级别上，问题的符号表示及其处理过程的机械化、严格化的 固有特性，决定了数学是计算机科学与技术学科的重要基础之一，数学及其形式 化描述、严密的表达和计算是计算机科学与技术学科所用的重要工具，建立物理 符号系统并对其实施变换是计算机科学与技术学科进行问题描述和求解的重要 手段。随着信息时代的到来，离散数学也越来越显得重要。作为一个学习计算机 技术学科的学生除了接受学好传统意义上的数学外应该格外重视离散数学的学 习。离散数学是计算机科学的基础内容，计算机技术的许多领域都要用到离散数 学中的概念。离散数学正因为它是以研究离散量的结构和相互间的关系为主要目 标，因此它充分描述了计算机科学离散性的特点。离散数学将随着计算机科学的 发展而发展，离散数学在计算机科学中的数据结构、操作系统、编译理论、算法 分析、逻辑设计、系统结构、容错诊断、机器定理证明等各方面体现着重要价值。 9 参考文献 [1]赵明珠, 毛家发, 陈婉君, 郑建炜.面向信息安全专业的立体信息化离散数 学互动式教学方法设计[J].计算机教育, 2016 (03) :32-33. [2]刘宏月, 张行进, 朱维军, 邓淼磊, 杨卫东, 张红梅.面向信息安全学科的 离散数学教学探究[J].计算机教育, 2012 (15) :23-26. [3]孙登第,丁转莲,程凡.面向信息安全的离散数学理实一体教学探索[J].电脑 知识与技术,2019,15(13):121-122+125. [4] 陈 敏, 李 泽 军. 离 散 数 学 在 计 算 机 学 科 中 的 应 用[J]. 电 脑 知 识 与 技 术,2009,5(01):251-252.