多目标优化入门讲义.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：56.66M 资料格式：pdf 举报版权申诉

windows_peng-9587103-4744302543463383376.pdf-第1页.png

第1页 / 共160页

windows_peng-9587103-4744302543463383376.pdf-第2页.png

第2页 / 共160页

windows_peng-9587103-4744302543463383376.pdf-第3页.png

第3页 / 共160页

windows_peng-9587103-4744302543463383376.pdf-第4页.png

第4页 / 共160页

windows_peng-9587103-4744302543463383376.pdf-第5页.png

第5页 / 共160页

windows_peng-9587103-4744302543463383376.pdf-第6页.png

第6页 / 共160页

windows_peng-9587103-4744302543463383376.pdf-第7页.png

第7页 / 共160页

windows_peng-9587103-4744302543463383376.pdf-第8页.png

第8页 / 共160页

文本预览

4. Multiobjective Optimization

4. Multiobjective Optimization 1 2 3 Basic Concepts of Multiobjective Optimization 1.1 Multiobjective Optimization Problem (MOP) 1.2 Pareto (or Nondominated) Optimal Solutions 1.3 Preference Structures Multiobjective Genetic Algorithm 2.1 Features of Genetic Search & Fitness Assignment Mechanism 2.2 Fitness Sharing & Population Diversity 2.3 Concept of Pareto Solution & Pareto GA Procedure Fitness Assignment Mechanism 3.1 Vector Evaluation Approach 3.2 Pareto Ranking Approach 3.3 Weighted-sum Approach 3.4 Elitist Preserve Approach

4. Multiobjective Optimization 4 Compromise Approach & Distance Method 4.1 Compromise Approach 4.2 Distance Method 4 Performance Measures 5.1 Reference solution set S* 5.2 Performance Measures 5 Applications of Multiobjective Optimization Problems 6.1 Bicriteria Linear Transportation Problem 6.2 Bicriteria Minimum Spanning Tree Problem 6.3 Bicriteria Nonlinear Programming Problem 6.4 Bicriteria Network Design Problem

4. Multiobjective Optimization 1 Basic Concepts of Multiobjective Optimization 1.1 Multiobjective Optimization Problem (MOP) 1.2 Pareto (or Nondominated) Optimal Solutions 1.3 Preference Structures 2 3 4 4 5 Multiobjective Genetic Algorithm Fitness Assignment Mechanism Compromise Approach & Distance Method Performance Measures Applications of Multiobjective Optimization Problems

1.1 Multiobjective Optimization Problem (MOP)      Optimization deals with the problem of seeking solutions over a set of possible choices to optimize certain criteria. 所谓的优化就是在某种规则下，使得个体的性能最优！ Multiobjective Optimization Problems (MOP) arise in the design, modeling, and planning of many complex real systems. Almost every important real-world decision making problem involves multiple and conflicting objectives.   Genetic Algorithms have received considerable attention as a novel approach to multiobjective optimization problem. Need to be tackled while respecting various constraints Leading to overwhelming problem complexity. (实际优化问题的目标函数往往是多个且相互冲突)

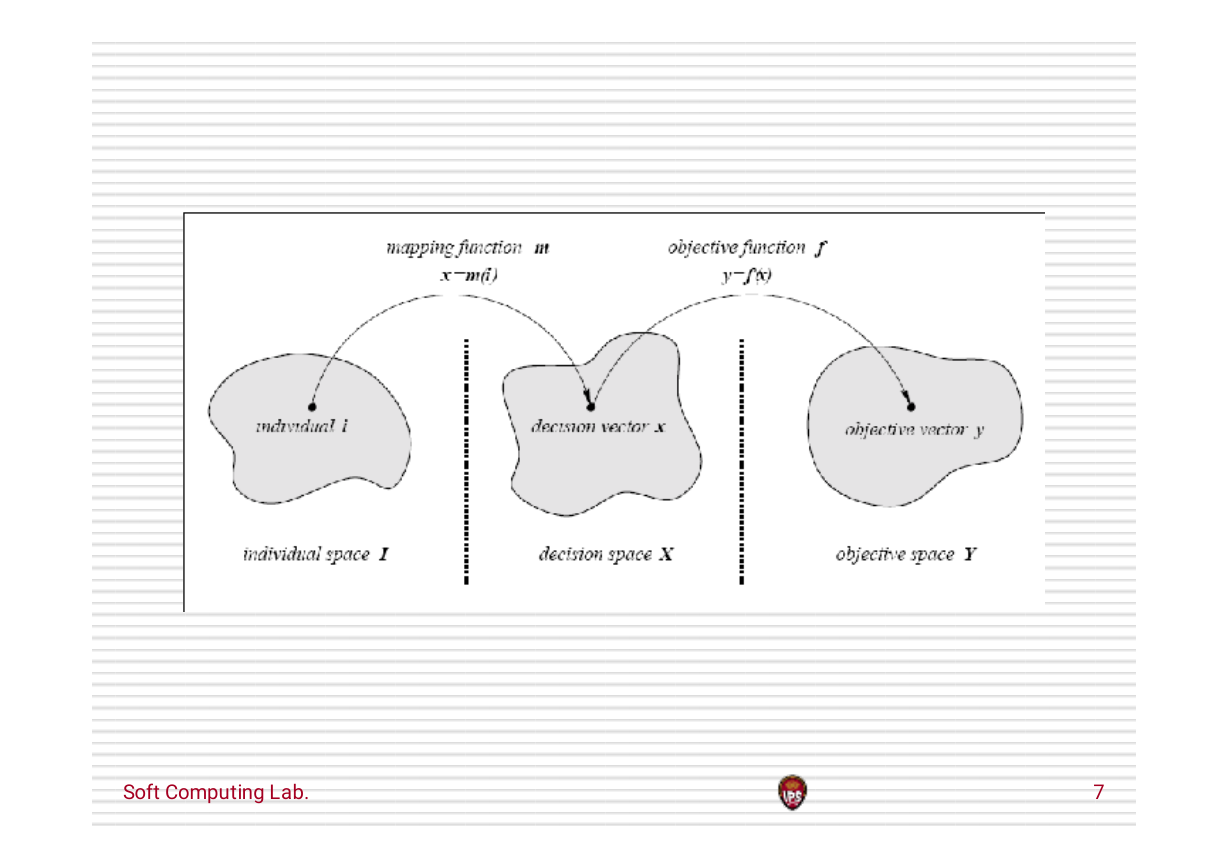
1.1 Multiobjective Optimization Problem (MOP) Multiobjective optimization problem with q objective functions  and m nonlinear constraints can be represented:   , (  f 2  ,2,1 i  ), x  ,  z q f q ( x )} ( f 1   z 1 x ( )  0 max { ), x z 2 ,0 m s. t. g i x The feasible region in the decision space denoted by the set S, is as follows:(决策空间,可行域) The feasible region in the criterion space denoted by the set Z, is as follows:(目标空间)  { n |R ,2,1 g i  , , m ( ) x i  S }0  x  ,0 x Z  z { q |R  z 1 f 1 ( x ), z 2  f 2 ( ), x  , z q  f q ( xx ),  } S

Soft Computing Lab. 7

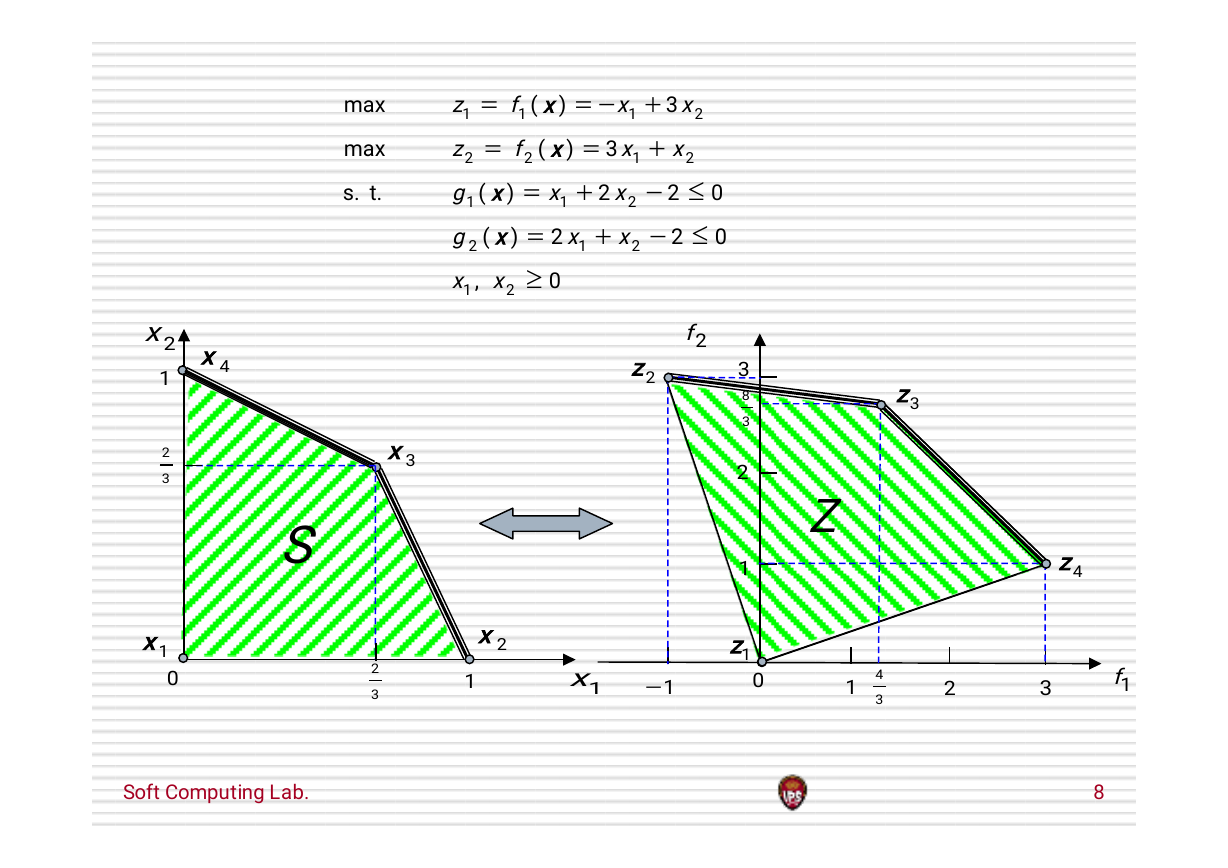
z 1 z 2 g 1 g 2 ,   ) ( x ( x ) ( f 1 ( f 2    xx 2 1 ) x 3 3 ) x x 2  x 1   xx 1 2   x x 2 2 1 2   xx 2 1 2 2 0 2f 2z max max s. t. 3x S 2x 1 2 3 1x 1 0 0 3 8 3 2 1 1z 0 3z Z 4z 1 4 3 2 3 1f 4x 2x 1 2 3 1x 0 Soft Computing Lab. 8

分享到：

赞收藏

资料库

多目标优化入门讲义.pdf

相关推荐

课程资源

热门标签

最新资料