2022年湖北武汉中考数学试题及答案.doc-资料库

第1页 / 共12页

第2页 / 共12页

第3页 / 共12页

第4页 / 共12页

第5页 / 共12页

第6页 / 共12页

第7页 / 共12页

第8页 / 共12页

2022 年湖北武汉中考数学试题及答案亲爱的同学：在你答题前，请认真阅读下面的注意事项. 1. 本试卷由第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分组成.全卷共 6 页，三大题，满分 120 分.考试用时 120 分钟. 2. 答题前，请将你的姓名、准考证号填写在“答题卡”相应位置，并在“答题卡”背面左上角填写姓名和座位号. 3. 答第Ⅰ卷（选择题）时，选出每小题答案后，用 2B 铅笔把“答题卡”上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案.答在．．“．试卷．．”．上无效．．．. 4. 答第Ⅱ卷（非选择题）时，答案用 0.5 毫米黑色笔迹签字笔书写在“答题卡”上. 答．在．“．试卷．．”．上无效．．．. 5. 认真阅读答题卡上的注意事项. 预祝你取得优异成绩！第Ⅰ卷（选择题共 30 分）一、选择题（共 10 小题，每小题 3 分，共 30 分）下列各题中有且只有一个正确答案，请在答题卡上将正确答案的标号涂黑. 1. 实数 2022 的相反数是（ A. －2022 B.  ） 1 2022 2. 彩民李大叔购买 1 张彩票，中奖.这个事件是（ C. 1 2022 ） D. 2022 A. 必然事件 B. 确定性事件 C. 不可能事件 D. 随机事件 3. 现实世界中，对称现象无处不在，中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是（） A. 4. 计算 122a A. B. C. D. 342a 的结果是（） B. 128a C. 76a D. 78a 5. 如图是由 4 个相同的小正方体组成的几何体，它的主视图是（） A. B. C. D.

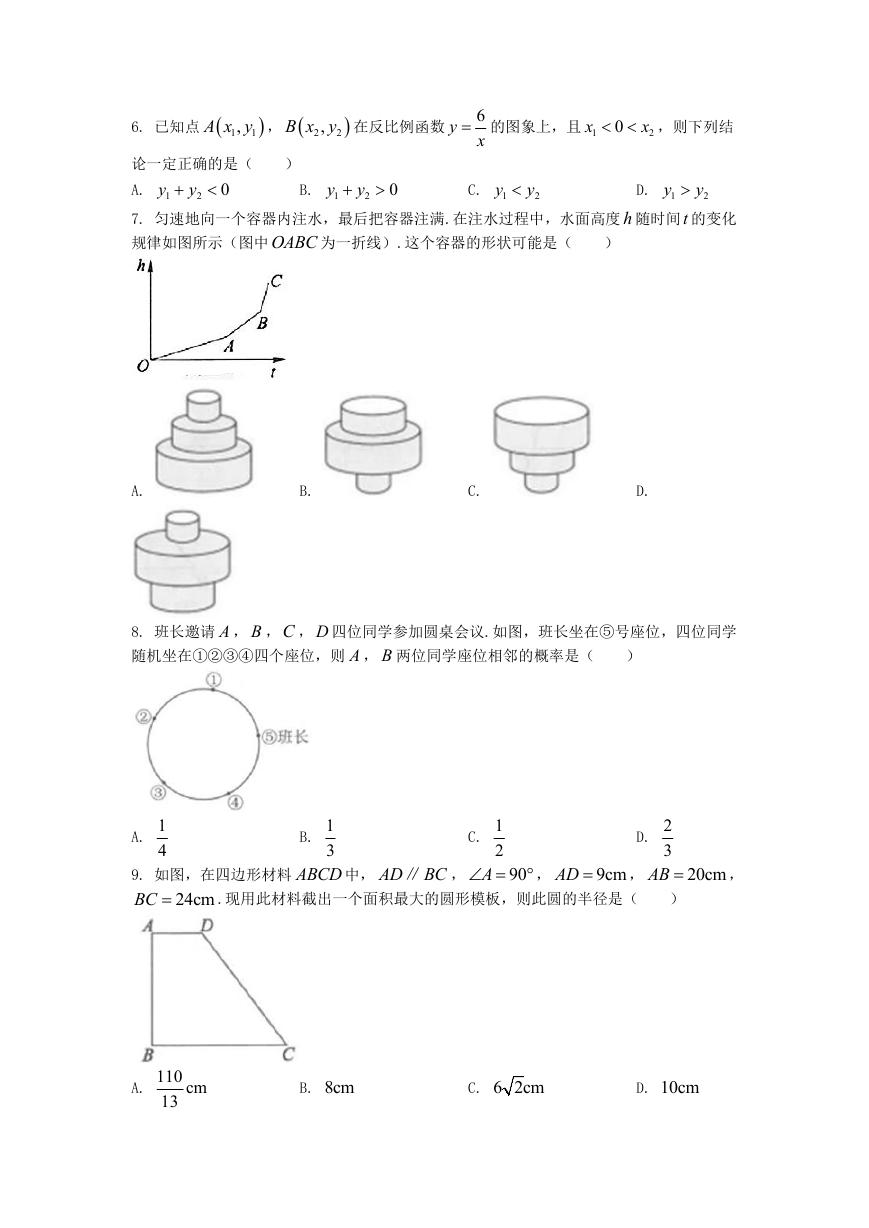
6. 已知点  ,A x y ，   1 1 B x y 在反比例函数 , 2  2 y x  的图象上，且 1 6 x   ，则下列结 0 x 2 论一定正确的是（） y 1 y  0 2 B. A. 7. 匀速地向一个容器内注水，最后把容器注满.在注水过程中，水面高度 h 随时间t 的变化规律如图所示（图中OABC 为一折线）.这个容器的形状可能是（ C. D. ） 2 2 2 y 1 y y 1 y  0 y 1 y A. B. C. D. 8. 班长邀请 A ， B ，C ， D 四位同学参加圆桌会议.如图，班长坐在⑤号座位，四位同学随机坐在①②③④四个座位，则 A ， B 两位同学座位相邻的概率是（） A. 1 4 B. 1 3 9. 如图，在四边形材料 ABCD 中， AD BC∥ ， BC  9cm .现用此材料截出一个面积最大的圆形模板，则此圆的半径是（ 24cm AD   ， 90 ， 20cm ， C. 1 2 A  D. 2 3 AB  ） A. 110 cm 13 B. 8cm C. 6 2cm D. 10cm

10. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格.将 9 个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的 3 个数之和相等，例如图（1）就是一个幻方.图（2）是一个未完成的幻方，则 x 与 y 的和是（） A. 9 B. 10 C. 11 D. 12 二、填空题（共 6 小题，每小题 3 分，共 18 分）第Ⅱ卷（非选择题共 90 分）下列各题不需要写出解答过程，请将结果直接填写在答题卡指定的位置. 11. 计算  12. 某体育用品专卖店在一段时间内销售了 20 双学生运动鞋，各种尺码运动鞋的销售量如 22 的结果是_________. 下表.则这 20 双运动鞋的尺码组成的一组数据的众数是_________. 尺码/ cm 销售量/双 2 x 2  x 13. 计算 24 1 1  x 3  9 24.5 3 25 10 25.5 4 26 2 的结果是_________. 14. 如图，沿 AB 方向架桥修路，为加快施工进度，在直线 AB 上湖的另一边的 D 处同时 ABC 施工.取 _________ m .  ，则 C ， D 两点的距离是 1600m BCD BC  150 105  ，，   2 y   ax  （ a ，b ，c 是常数）开口向下，过  A  c  .下列四个结论： bx 1,0 ，  B m 两 ,0 15. 已知抛物线点，且1 2m ① 0b  ； 3 2 ③若点  1 ④当 ②若 1 m  ，则3 a  2 c ,M x y ，   ； 0  a   时，关于 x 的一元二次方程 2 ax N x y 在抛物线上， 1 x bx  1 2 2 , x 2 x ，且 1 y ； x   必有两个不相等的实数根. 1 y  ，则 1 2 c 1 2 其中正确的是_________（填写序号）. 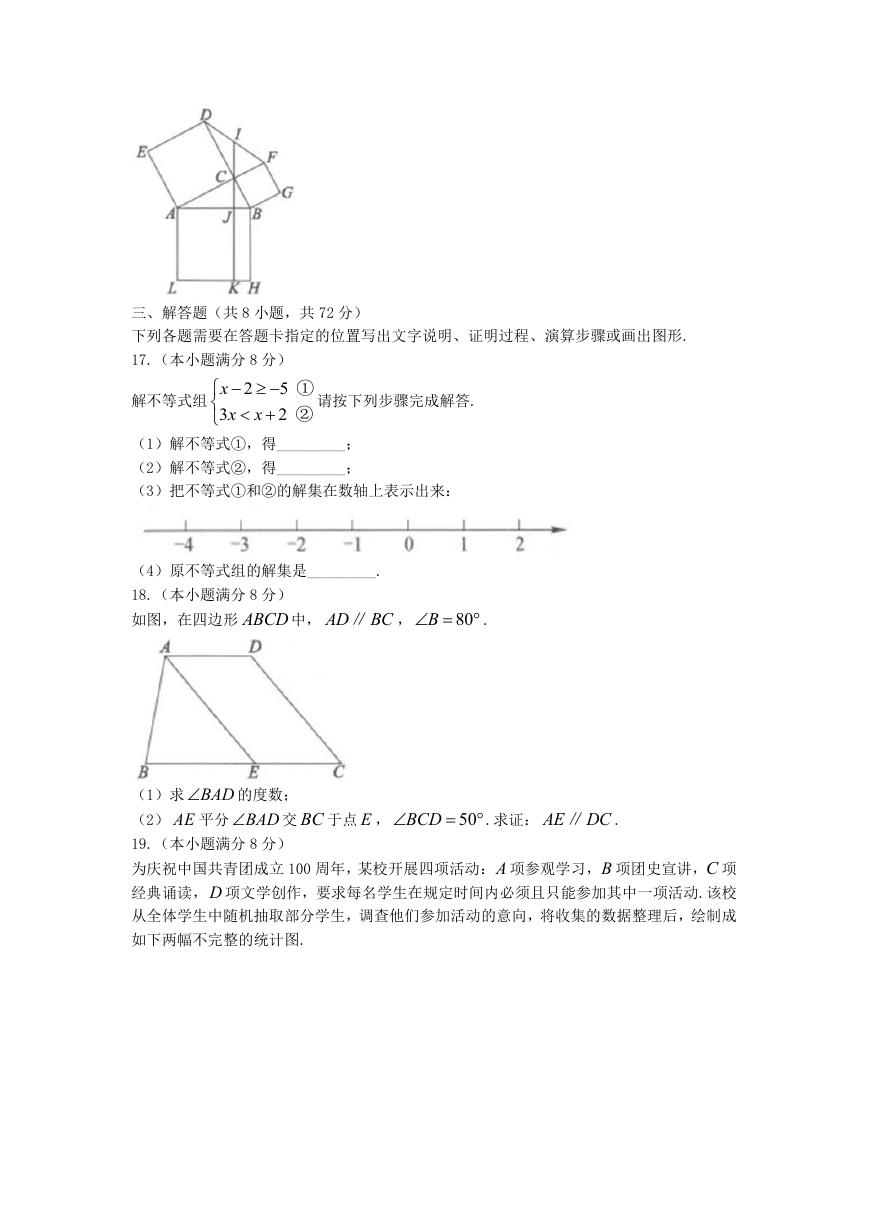16. 如图，在 Rt ABC△  作三个正方形 ABHL ，ACDE ，BCFG ，连接 DF .过点 C 作 AB 的垂线CJ ，垂足为 J ， CJ  ，则四边形 AJKL 的面积是_________. 分别交 DF ， LH 于点 I ， K .若  ， AC BC ，分别以 ABC△ 的三边为边向外 CI  ， ACB 中， 90 5 4

三、解答题（共 8 小题，共 72 分）下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形. 17.（本小题满分 8 分） 2 5 x      3 2 x    解不等式组 x ① ② 请按下列步骤完成解答. （1）解不等式①，得_________；（2）解不等式②，得_________；（3）把不等式①和②的解集在数轴上表示出来：（4）原不等式组的解集是_________. 18.（本小题满分 8 分）如图，在四边形 ABCD 中， AD BC∥ ， B  80  . 的度数；  50 交 BC 于点 E ，（1）求 BAD （2） AE 平分 BAD 19.（本小题满分 8 分）为庆祝中国共青团成立 100 周年，某校开展四项活动：A 项参观学习，B 项团史宣讲，C 项经典诵读，D 项文学创作，要求每名学生在规定时间内必须且只能参加其中一项活动.该校从全体学生中随机抽取部分学生，调查他们参加活动的意向，将收集的数据整理后，绘制成  .求证： AE DC∥ . BCD 如下两幅不完整的统计图.

（1）本次调查的样本容量是__________， B 项活动所在扇形的圆心角的大小是_________，条形统计图中C 项活动的人数是_________；（2）若该校约有 2000 名学生，请估计其中意向参加“参观学习”活动的人数. 20.（本小题满分 8 分）如图，以 AB 为直径的 O 经过 ABC△ AE 的延长线交 O 于点 D ，连接 BD . 的顶点C ， AE ，BE 分别平分 BAC 和 ABC ，（1）判断 BDE△ 10 AB  ，（2）若的形状，并证明你的结论；，求 BC 的长. BE  21.（本小题满分 8 分）如图是由小正方形组成的9 6 网格，每个小正方形的顶点叫做格点. ABC△ 是格点.仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示. 2 10 的三个顶点都（1）在图（1）中，D ，E 分别是边 AB ，AC 与网格线的交点.先将点 B 绕点 E 旋转180 得到点 F ，画出点 F ，再在 AC 上画点G ，使 DG BC∥ ；（2）在图（2）中， P 是边 AB 上一点， BAC  到线段 AH ，画出线段 AH ，再画点 Q ，使 P ，Q 两点关于直线 AC 对称. 22.（本小题满分 10 分）在一条笔直的滑道上有黑、白两个小球同向运动，黑球在 A 处开始减速，此时白球在黑球前面 70cm 处.  .先将 AB 绕点 A 逆时针旋转 2，得 

小聪测量黑球减速后的运动速度 v （单位：cm/s ）、运动距离 y （单位：cm ）随运动时间 t （单位：s ）变化的数据，整理得下表. 运动时间 / st 运动速度 / cm/s v 9.5 8.5 10 1 2 3 4 9 8 0 0 19 9.75 27.75 运动距离 / cmy 小聪探究发现，黑球的运动速度 v 与运动时间t 之间成一次函数关系，运动距离 y 与运动时间t 之间成二次函数关系. （1）直接写出 v 关于t 的函数解析式和 y 关于t 的函数解析式（不要求写出自变量的取值范围）（2）当黑球减速后运动距离为 64cm 时，求它此时的运动速度；（3）若白球一．直．以 2cm/s 的速度匀速运动，问黑球在运动过程中会不会碰到白球？请说明理由. 36 23.（本小题满分 10 分）问题提出如图（1）， ABC△ ， D 是 AC 的中点，延长 BC 至点 E ，使 DE DB ，延长 ED 交 AB 于点 F ，探究的值. 中， AB AC AF AB 问题探究（1）先将问题特殊化.如图（2），当 BAC  60  时，直接写出 AF AB 的值；（2）再探究一般情形.如图（1），证明（1）中的结论仍然成立. 问题拓展如图（3），在 ABC△ 1 CG BC n 的值（用含 n 的式子表示）.  ，延长 BC 至点 E ，使 DE DG 中， AB AC 2  n   ， D 是 AC 的中点，G 是边 BC 上一点， AF AB ，延长 ED 交 AB 于点 F .直接写出 24.（本小题满分 12 分） y  x 2 2  x 抛物线点，直线 AC 交 y 轴于点 P .  交 x 轴于 A ， B 两点（ A 在 B 的左边），C 是第一象限抛物线上一 3

（1）直接写出 A ， B 两点的坐标；（2）如图（1），当OP OA 时，在抛物线上存在点 D（异于点 B ），使 B ，D 两点到 AC 的距离相等，求出所有满足条件的点 D 的横坐标；（3）如图（2），直线 BP 交抛物线于另一点 E ，连接CE 交 y 轴于点 F ，点C 的横坐标为 m .求 FP OP 的值（用含 m 的式子表示）. 一、选择题（共 10 小题，每小题 3 分，共 30 分）数学试题参考答案题号答案 1 A 2 D 3 D 4 B 5 A 6 C 7 A 8 C 9 B 10 D 二、填空题（共 6 小题，每小题 3 分，共 18 分） 11. 2 12. 25 13. 1 3x  三、解答题（共 8 小题，共 72 分） 3 x   17.（1）（2） 1x  14. 800 2 15. ①③④ 16. 80 1x    （3）（4） 3 18.（1）解：∵ AD BC∥ ， ∴  ， 180  ∵ B BAD    80 B   ， 100 BAD   . ∴ （2）证明：∵ AE 平分 BAD ∵ AD BC∥ ，∴   50  ，∴ BCD ∵ ∴ AE DC∥ . AEB  BCD    50  . DAE ，∴ 50 DAE   . AEB   .

另解：运用三角形内角和也可以得证. 19.（1）80，54 ，20 （2）解： 2000  32 80  800 （人）. CBE ，      .   CBD ABE ， EBC DBC CAD BAE DBE       . ， BE 平分 ABC     ， ABE ， DBE 为等腰直角三角形，理由如下： ∴该校意向参加“参观学习”活动的学生大约有 800 人. 20.（1） BDE△ 证明：∵ AE 平分 BAC ∴ BAE   ∵ BED   ∴ BED . ∴ BD ED ∵ AB 为直径，∴ ∴ BDE△ 另解：计算（2）解：连接OC ，CD ，OD ，OD 交 BC 于点 F . ∵ DBC ∴ BD DC ∵OB OC ∴OD 垂直平分 BC . ∵ BDE△ 90 是等腰直角三角形. AEB 是等腰直角三角形，  也可以得证.   . ADB   BAD   BCD BE  2 10  135   . ，  CAD ，， 5  . OB OD DF t   . 和 Rt BDF△ 5 ∴ 2 5 10 BD  . AB  ，∴ ∵ 设OF t ，则在 Rt BOF△ 解得， 3t  . 4 BF  . ∴ 8 BC  . 中， 2 5 2  t  (2 5) 2  (5  2 t ) . ∴ 另解：分别延长 AC ， BD 相交于点G .则 ABG△ BG  ，再根据面积相等求得 BC . AD  4 5 4 5 ，为等腰三角形，先计算 AG  ， 10

资料库

2022年湖北武汉中考数学试题及答案.doc

相关推荐

中考

热门标签

最新资料