最小二乘法的基本原理和多项式拟合matlab实现.doc-资料库

最小二乘法的基本原理和多项式拟合一、最小二乘法的基本原理从整体上考虑近似函数 )(xp 同所给数据点 ( xp  y )  r i r i ( , i yx i ) (i=0,1,…,m)误差 i i (i=0,1,…,m) 的大小，常用的方法有以下三种：一是误差  ( xp i )  y i (i=0,1,…,m)绝对值的最大值 max r imi 0 ，即误差向量 r  ( , rr 0  1 , mr T ) 的∞—范数；二是误差绝对值的和 m  ir 0 ，即误差向量 r 的 1—  i 范数；三是误差平方和 m  i  0 2 ir 的算术平方根，即误差向量 r 的 2—范数；前两种方法简单、自然，但不便于微分运算，后一种方法相当于考虑 2—范数的平方，因此在曲线拟合中常采用误差平方和体大小。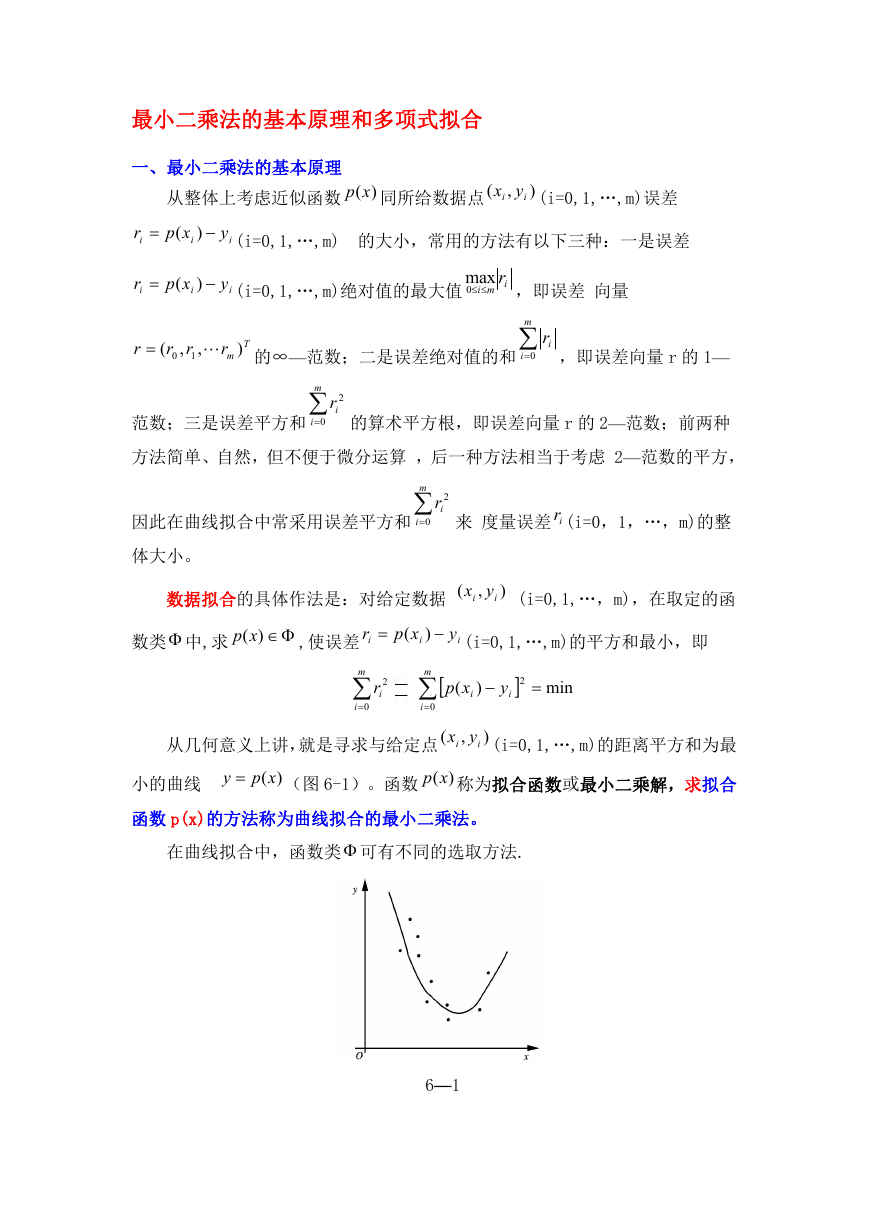 m  i  0 2 ir 来度量误差 ir (i=0，1，…，m)的整数据拟合的具体作法是：对给定数据 ( , i yx i ) (i=0,1,…，m)，在取定的函数类  中,求 )(xp ,使误差 r i  ( xp i )  y i (i=0,1,…,m)的平方和最小，即 m  i  0 2 ir m  i  0  ( xp i )  y i  2 min  从几何意义上讲，就是寻求与给定点 (i=0,1,…,m)的距离平方和为最（图 6-1）。函数 )(xp 称为拟合函数或最小二乘解，求拟合 i 小的曲线 y  )(xp ( , i yx ) 函数 p(x)的方法称为曲线拟合的最小二乘法。在曲线拟合中，函数类  可有不同的选取方法. 6—1

二多项式拟合假设给定数据点 ( , i yx i ) (i=0,1,…,m)， 为所有次数不超过 ( mnn  的多项式构 ) 成的函数类，现求一 )( xp n n   k  0 k xa k  ,使得 I m   i  0  ( xp n i )  y i 2   n m   i  0 k  0    xa k k i  y i 2    min 当拟合函数为多项式时，称为多项式拟合，满足式（1）的 (1) )(xpn 称为最小二乘拟合多项式。特别地，当 n=1 时，称为线性拟合或直线拟合。显然 I  n m   ( i  0 k  0 xa k k i  y i 2 ) aa , 0 , 1 na 的多元函数，因此上述问题即为求 I  , ( aaI 1 0 ,  na ) 的极值问题。为由多元函数求极值的必要条件，得 I  a  j  2 即 n m   ( i  0 k  0 xa k k i  j ) xy i i  ,0 j  ,1,0 , n j yx i i , j  ,1,0 , n (2) (3) n  k  0 ( m  i  0 kj  x i ) a k  m  i  0 （3）是关于 aa , 0 , 1 na 的线性方程组，用矩阵表示为             m  1 i m x i   0  x m i  0 i 2 i m x 0 i  m   x 0  x m  i n i  n i i  0 1   m  i  0 n 2 i m 0   i  m i  0 x n i 1  n i x  x           a 0 a 1  a n                        m   i  m i  0 y i i 0 yx i  n yx i i m  i  0           (4) 式（3）或式（4）称为正规方程组或法方程组。可以证明，方程组（4）的系数矩阵是一个对称正定矩阵，故存在唯一解。从式（4）中解出 ka (k=0,1,…，n)，从而可得多项式

)( xp n  n  k  0 k xa k (5) 可以证明，式（5）中的 )(xpn 满足式（1），即 )(xpn 为所求的拟合多项式。我 m  i  0 们把  ( xp n i )  y i 2  称为最小二乘拟合多项式 )(xpn 的平方误差，记作 r 2 2  m  i  0  ( xp n i )  y i 2  由式(2)可得 r 2 2  m  i  0 y 2 i  n m   a ( k k  0 i  0 k yx i i ) (6) 多项式拟合的一般方法可归纳为以下几步： (1) 由已知数据画出函数粗略的图形——散点图，确定拟合多项式的次数 n； (2) 列表计算 m  i  0 j x i ( j  ,1,0  )2, n 和 m  i  0 j yx i i ( j  ,1,0  )2, n ； (3) 写出正规方程组，求出 aa , 0 , 1 na ； )( xp n  n  k xa k (4) 写出拟合多项式在实际应用中， mn  或 mn  ；当 mn  时所得的拟合多项式就是拉格朗日或牛。 0  k 顿插值多项式。例 1 测得铜导线在温度 iT (℃)时的电阻 (iR 如表 6-1，求电阻 R 与温度 T ) 的近似函数关系。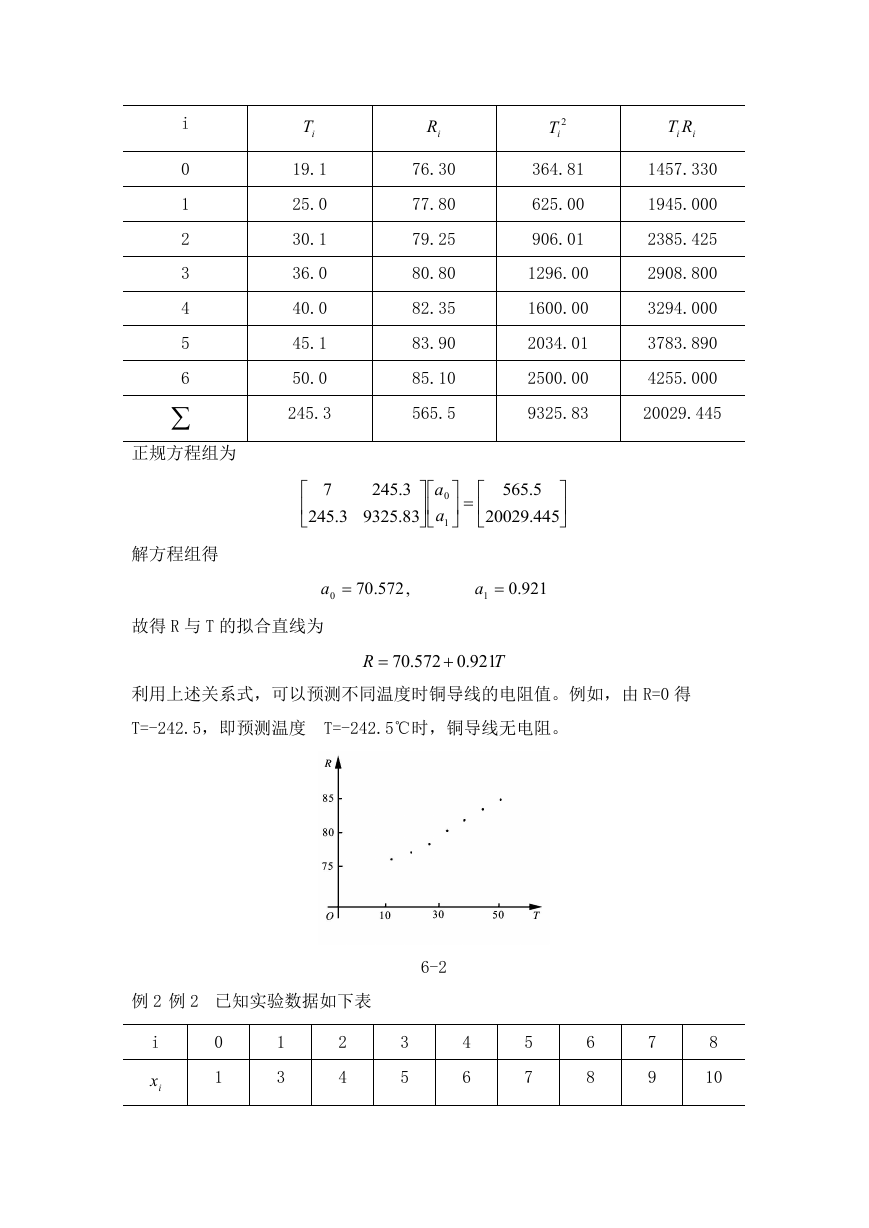 i 0 1 2 3 4 5 6 iT (℃) (iR ) 19.1 25.0 30.1 36.0 40.0 45.1 50.0 76.30 77.80 79.25 80.80 82.35 83.90 85.10 解画出散点图（图 6-2），可见测得的数据接近一条直线，故取 n=1，拟合函数为列表如下 aR  0  Ta 1

i 0 1 2 3 4 5 6  iT 19.1 25.0 30.1 36.0 40.0 45.1 50.0 245.3 iR 76.30 77.80 79.25 80.80 82.35 83.90 85.10 565.5 2 iT 364.81 625.00 906.01 i RT i 1457.330 1945.000 2385.425 1296.00 2908.800 1600.00 3294.000 2034.01 3783.890 2500.00 4255.000 9325.83 20029.445 正规方程组为解方程组得 7 3.245    3.245   83. 9325  a 0 a 1          5.565   445.  20029 a 0  .70 572 , a 1  .0 921 故得 R 与 T 的拟合直线为 R  572.70  921.0 T 利用上述关系式，可以预测不同温度时铜导线的电阻值。例如，由 R=0 得 T=-242.5，即预测温度 T=-242.5℃时，铜导线无电阻。例 2 例 2 已知实验数据如下表 6-2 i ix 0 1 1 3 2 4 3 5 4 6 5 7 6 8 7 9 8 10

iy 10 5 4 2 1 1 2 3 4 试用最小二乘法求它的二次拟合多项式。解设拟合曲线方程为 y  a 0  xaxa 2 1  2 列表如下 I 0 1 2 3 4 5 6 7 8  ix 1 3 4 5 6 7 8 9 10 53 iy 10 5 4 2 1 1 2 3 4 32 2 ix 1 9 16 25 36 49 64 81 3 ix 1 27 64 125 216 343 512 729 100 381 1000 3017 4 ix 1 81 256 625 1296 2401 4096 6561 10000 i yx i i yx 2 i 10 15 16 10 6 7 16 27 40 10 45 64 50 36 49 128 243 400 25317 147 1025 得正规方程组解得故拟合多项式为 9   52   381  52 381 3017 381 3017 25317      a 0 a 1 a 2            32   147   1025       a 0  .13 4597 , a 1  .3 6053 a 2  .0 2676 y  .13 4597  .3 6053  .0 2676 x 2 *三最小二乘拟合多项式的存在唯一性定理 1 设节点 , xx 0  互异，则法方程组（4）的解存在唯一。 1 nx , , 证由克莱姆法则，只需证明方程组（4）的系数矩阵非奇异即可。用反证法，设方程组（4）的系数矩阵奇异，则其所对应的齐次方程组

            m  1 i m x i   0  x m i  0 i 2 i m x 0 i  m   x 0  x m  i n i m 0   i  m i  0 x n i 1  n i x  x           a 0 a 1  a n                        m   i  m i  0 y i i 0 yx i  n yx i i m  i  0  n i i  0 1   m  i  0 n 2 i 有非零解。式(7)可写为 n m   ( k  0 i  0 kj  x i ) a k  ,0 j  ,1,0 , n           （7）（8）将式（8）中第 j 个方程乘以 ja (j=0,1,…，n)，然后将新得到的 n+1 个方程左右两端分别相加，得因为 n m    kj  x i a ( j j 0  0  i 0  n    k  0) a  k  0 n n m    a ( j k  0 i  0    j  0 kj  x i ) a k    m  i  0 n n  j  0 k  0 xaa j k i kj   m  i  0 ( n  j  0 j xa j i )( n  k  0 xa k k i )   ( xp n i 2  ) m  i  0 其中所以 )( xp n  n  k  0 k xa k ( n xp ) i 0 (i=0,1,…,m) )(xpn 是次数不超过 n 的多项式，它有 m+1＞n 个相异零点，由代数基本定理，必 a 0  a 1   na  0 须有，与齐次方程组有非零解的假设矛盾。因此正规方程组（4）必有唯一解。定理 2 设 ,1,0  是正规方程组（4）的解，则 aa na , )( xp n  是满足式（1）的最小二乘拟合多项式。 n  k  0 k xa k 证只需证明，对任意一组数 ,1,0  组成的多项式 bb nb , )( xQ n  m  i  0  ( xQ n i )  y i 2    ( xp n i )  y i 2  m  i  0 n  k  0 k xb k ，恒有

 ( xQ n i )  ( xp n i    ) ( xp n i )  y i  n i     k i 即可。  ( xQ n i )  y i 2   m  i  0 m  i  0  ( xp n i )  y i 2   m  i  0  ( xQ n i )  ( xp n i 2  )  2 m  0 m n   ( b  20         因为 ka (k=0,1,…，n)是正规方程组（4）的解，所以满足式（2），因此有       b      ) xa j       xa k xa k      2    i  0 i  0 a  x y y  0  0  0  0 k i j i j i k i m  n j i n k j j j j  ( xQ n i )  y i 2   m  i  0 m  i  0  ( xp n i )  y i 2   0 )(xpn 为最小二乘拟合多项式。故 *四多项式拟合中克服正规方程组的病态在多项式拟合中，当拟合多项式的次数较高时，其正规方程组往往是病态的。而且 ①正规方程组系数矩阵的阶数越高，病态越严重； ②拟合节点分布的区间 ③ ix (i=0,1,…，m)的数量级相差越大，病态越严重。 x ,0 偏离原点越远，病态越严重； mx 为了克服以上缺点，一般采用以下措施： ①尽量少作高次拟合多项式，而作不同的分段低次拟合； ②不使用原始节点作拟合，将节点分布区间作平移，使新的节点 ix 关于原点对称，可大大降低正规方程组的条件数，从而减低病态程度。平移公式为： x i  x i  x 0 x m ,  2 i  ,1,0 , m (9) ③对平移后的节点 ix (i=0,1,…，m),再作压缩或扩张处理： x  i xp i , i  ,1,0 , m （10） p  2 r ( m  )1 其中 m  i  0 ( ix r 2) ,（r 是拟合次数）（11）经过这样调整可以使  ix 的数量级不太大也不太小，特别对于等距节点

xi  x 0  ih ( i  ,1,0 , m ) ，作式（10）和式（11）两项变换后，其正规方程组的系数矩阵设为 A，则对 1～4 次多项式拟合，条件数都不太大，都可以得到满意的结果。变换后的条件数上限表如下：拟合次数 cond ) (2 A 1 =1 2 <9.9 3 <50.3 4 <435 ④在实际应用中还可以利用正交多项式求拟合多项式。一种方法是构造离散正交多项式；另一种方法是利用切比雪夫节点求出函数值后再使用正交多项式。这两种方法都使正规方程组的系数矩阵为对角矩阵，从而避免了正规方程组的病态。我们只介绍第一种，见第三节。例如 m=19, 0x =328,h=1, 1x = 0x +ih，i=0,1,…，19，即节点分布在［328,347］，作二次多项式拟合时 ① 直接用 ix 构造正规方程组系数矩阵 0A ，计算可得 cond ( A 0 ) 2 25.2  10 16 严重病态，拟合结果完全不能用。 ② 作平移变换 x i  x i  328 347 ,  2 i  ,1,0 19, 用 ix 构造正规方程组系数矩阵 1A ，计算可得 cond ( A 1 ) 2 .4 483868  10 16 cond ( 0 2 A ) 比降低了 13 个数量级，病态显著改善，拟合效果较好。 ③ 取压缩因子  .0 1498 20 ix ( 4 ) p  4 19  i 0 作压缩变换 x  i xp i , i  ,1,0 19,  ix 构造正规方程组系数矩阵 2A ，计算可得用 cond ( 2 A ) 2 839.6

资料库

最小二乘法的基本原理和多项式拟合matlab实现.doc

相关推荐

课程资源

热门标签

最新资料