透射型体光栅对超短脉冲高斯光束衍射特性研究.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：2.97M 资料格式：pdf 举报版权申诉

weixin_38650150-15215553-16359647481279101748.pdf-第1页.png

第1页 / 共6页

weixin_38650150-15215553-16359647481279101748.pdf-第2页.png

第2页 / 共6页

weixin_38650150-15215553-16359647481279101748.pdf-第3页.png

第3页 / 共6页

weixin_38650150-15215553-16359647481279101748.pdf-第4页.png

第4页 / 共6页

weixin_38650150-15215553-16359647481279101748.pdf-第5页.png

第5页 / 共6页

weixin_38650150-15215553-16359647481279101748.pdf-第6页.png

第6页 / 共6页

文本预览

第２９卷　第１期２００９年１月光　学　学　报犃犆犜犃犗犘犜犐犆犃犛犐犖犐犆犃Ｖｏｌ．２９，Ｎｏ．１犑犪狀狌犪狉狔，２００９文章编号：０２５３２２３９（２００９）０１０１２６０６透射型体光栅对超短脉冲高斯光束衍射特性研究郑光威１　刘　莉１　何焰蓝２　谭吉春２　郑浩斌２　王　逍３　王晓东３１国防科技大学光电科学与工程学院，湖南，长沙４１００７３；２国防科技大学理学院，湖南，长沙４１００７３）（３中国工程物理研究院激光聚变研究中心，四川，绵阳６２１９００摘要　采用傅里叶频谱分析法，将超短脉冲高斯光束展开为单色单角谱成分的线性叠加；利用Ｋｏｇｅｌｎｉｋ一维耦合波理论，分析透射型体光栅对各单色单角谱成分的衍射特性；再通过逆傅里叶变换得出衍射光波的时空分布与光栅各参量的对应关系。结果表明：衍射光束在时域以及在光栅波矢与光栅前表面法向所构成平面内的空域光强分布随光栅周期的减小而呈展宽趋势，且在空域的展宽趋势较为迅速，与入射光束在空域进行比较，衍射光束空域分布发生非常明显的畸变；衍射光束在时域以及在光栅波矢与光栅前表面法向所构成平面内的空域光强分布随光栅厚度的增大亦呈展宽趋势，且展宽速度相当，与入射光束在时域和空域比较，均发生了较明显的畸变。关键词　衍射与光栅；体光栅衍射特性；耦合波理论；超短脉冲高斯光束；傅里叶变换中图分类号　Ｏ４３８．１　　　文献标识码　Ａ　　　犱狅犻：１０．３７８８／犃犗犛２００９２９０１．０１２６犇犻犳犳狉犪犮狋犻狅狀犘狉狅狆犲狉狋犻犲狊狅犳犝犾狋狉犪犛犺狅狉狋犘狌犾狊犲犱犌犪狌狊狊犻犪狀犔犪狊犲狉犅犲犪犿犫狔犜狉犪狀狊犿犻狊狊犻狅狀犞狅犾狌犿犲犌狉犪狋犻狀犵犣犺犲狀犵犌狌犪狀犵狑犲犻１　犔犻狌犔犻１　犎犲犢犪狀犾犪狀２　犜犪狀犑犻犮犺狌狀２　犣犺犲狀犵犎犪狅犫犻狀２犠犪狀犵犡犻犪狅３　犠犪狀犵犡犻犪狅犱狅狀犵３１犆狅犾犾犲犵犲犗狆狋狅犲犾犲犮狋狉狅狀犻犮犛犮犻犲狀犮犲犪狀犱犈狀犵犻狀犲犲狉犻狀犵，犖犪狋犻狅狀犪犾犝狀犻狏犲狉狊犻狋狔狅犳犇犲犳犲狀犮犲犜犲犮犺狀狅犾狅犵狔，犆犺犪狀犵狊犺犪，犎狌狀犪狀４１００７３，犆犺犻狀犪烌烄２犆狅犾犾犲犵犲狅犳犛犮犻犲狀犮犲，犖犪狋犻狅狀犪犾犝狀犻狏犲狉狊犻狋狔狅犳犇犲犳犲狀狊犲犜犲犮犺狀狅犾狅犵狔，犆犺犪狀犵狊犺犪，犎狌狀犪狀４１００７３，犆犺犻狀犪３犚犲狊犲犪狉犮犺犆犲狀狋犲狉狅犳犔犪狊犲狉犉狌狊犻狅狀，犆犺犻狀犪犃犮犪犱犲犿狔狅犳犈狀犵犻狀犲犲狉犻狀犵犘犺狔狊犻犮狊，犕犻犪狀狔犪狀犵，犛犻犮犺狌犪狀６２１９００，犆犺犻狀犪烆烎犃犫狊狋狉犪犮狋　犅犪狊犲犱狅狀犉狅狌狉犻犲狉狋狉犪狀狊犳狅狉犿，狋犺犲狌犾狋狉犪狊犺狅狉狋狆狌犾狊犲犱犌犪狌狊狊犻犪狀犾犪狊犲狉犫犲犪犿犻狊狋狉犪狀狊犳狅狉犿犲犱犻狀狋狅犾犻狀犲犪狉犮狅犿犫犻狀犪狋犻狅狀狊狅犳犿狅狀狅犮犺狉狅犿犪狋犻犮狆犾犪狀犲狑犪狏犲狊．犇犲狆犲狀犱犻狀犵狅狀犓狅犵犲犾狀犻犽′狊狅狀犲犱犻犿犲狀狊犻狅狀犪犾犮狅狌狆犾犲犱狑犪狏犲狋犺犲狅狉狔，狋犺犲犱犻犳犳狉犪犮狋犻狅狀犮犺犪狉犪犮狋犲狉犻狊狋犻犮狊狅犳犿狅狀狅犮犺狉狅犿犪狋犻犮狆犾犪狀犲狑犪狏犲狊犫狔狋狉犪狀狊犿犻狋狋犻狀犵狏狅犾狌犿犲犵狉犪狋犻狀犵犪狉犲狆狌狋犳狅狉狑犪狉犱，狑犺犲狀狋犺犲犮犲狀狋狉犪犾狑犪狏犲狏犲犮狋狅狉狊犪狋犻狊犳犻犲狊狋犺犲犅狉犪犵犵犮狅狀犱犻狋犻狅狀狅犳狋犺犲狏狅犾狌犿犲犵狉犪狋犻狀犵．犠犻狋犺狋犺犲犻狀狏犲狉狊犲犉狅狌狉犻犲狉狋狉犪狀狊犳狅狉犿狅犳犱犻犳犳狉犪犮狋犻狅狀狅犳犿狅狀狅犮犺狉狅犿犪狋犻犮狆犾犪狀犲狑犪狏犲狊，狋犺犲犾犪狑狅犳狊狆犪狋犻犪犾犪狀犱狋犲犿狆狅狉犪犾犻狀狋犲狀狊犻狀犵犱犻狊狋狉犻犫狌狋犻狅狀狅犳犱犻犳犳狉犪犮狋犻狏犲犫犲犪犿狑犻狋犺犱犻犳犳犲狉犲狀狋狆犪狉犪犿犲狋犲狉狊狅犳狏狅犾狌犿犲犵狉犪狋犻狀犵犻狊犵犻狏犲狀．犜犺犲狉犲狊狌犾狋狊狊犺狅狑狋犺犪狋犱犻犳犳狉犪犮狋犻狏犲犾犪狊犲狉犫犲犪犿犻狊犫狉狅犪犱犲狀犲犱犻狀狋犺犲狋犲犿狆狅狉犪犾犪狀犱狊狆犪狋犻犪犾犱狅犿犪犻狀狊，犻狀狋犺犲狆犾犪狀犲犮狅犿狆狉犻狊犻狀犵狅犳狋犺犲犵狉犪狋犻狀犵狏犲犮狋狅狉犪狀犱狋犺犲狀狅狉犿犪犾狏犲犮狋狅狉狅犳狋犺犲犵狉犪狋犻狀犵犳狉狅狀狋狊狌狉犳犪犮犲，狑犻狋犺狋犺犲犱犲犮狉犲犪狊犻狀犵狆犲狉犻狅犱狅犳狋犺犲狋狉犪狀狊犿犻狋狋犻狀犵狏狅犾狌犿犲犵狉犪狋犻狀犵．犐狋狊犫狉狅犪犱犲狀犻狀犵狋狉犲狀犱犻狀狋犺犲狊狆犪狋犻犪犾犱狅犿犪犻狀犻狊犳犪狊狋犲狉狋犺犪狀狋犺犪狋犻狀狋犺犲狋犲犿狆狅狉犪犾犱狅犿犪犻狀．犆狅犿狆犪狉犲犱狑犻狋犺犻狀狆狌狋狌犾狋狉犪狊犺狅狉狋狆狌犾狊犲犱犌犪狌狊狊犻犪狀犾犪狊犲狉犫犲犪犿，狋犺犲犱犻犳犳狉犪犮狋犻狏犲犾犪狊犲狉犫犲犪犿犻狊犱犲狋犲狉犻狅狉犪狋犲犱狅犫狏犻狅狌狊犾狔犻狀狋犺犲狊狆犪狋犻犪犾犱狅犿犪犻狀．犇犻犳犳狉犪犮狋犻狏犲犾犪狊犲狉犫犲犪犿犻狊犫狉狅犪犱犲狀犲犱犻狀狋犺犲狋犲犿狆狅狉犪犾犪狀犱狊狆犪狋犻犪犾犱狅犿犪犻狀狊犻狀狋犺犲狆犾犪狀犲犮狅犿狆狉犻狊犻狀犵狅犳狋犺犲犵狉犪狋犻狀犵狏犲犮狋狅狉犪狀犱狋犺犲狀狅狉犿犪犾狏犲犮狋狅狉狅犳狋犺犲犵狉犪狋犻狀犵犳狉狅狀狋狊狌狉犳犪犮犲，狑犻狋犺狋犺犲犻狀犮狉犲犪狊犻狀犵狋犺犻犮犽狀犲狊狊狅犳狋犺犲犵狉犪狋犻狀犵．犃狀犱犻狋狊犫狉狅犪犱犲狀犻狀犵狋狉犲狀犱犻狊犲狇狌犪犾狋狅犲犪犮犺狅狋犺犲狉犻狀狋犺犲狊狆犪狋犻犪犾犪狀犱犻狀狋犲犿狆狅狉犪犾犱狅犿犪犻狀狊．犆狅犿狆犪狉犲犱狑犻狋犺狋犺犲犻狀狆狌狋狌犾狋狉犪狊犺狅狉狋狆狌犾狊犲犱犌犪狌狊狊犻犪狀犾犪狊犲狉犫犲犪犿，狋犺犲犱犻犳犳狉犪犮狋犻狏犲犾犪狊犲狉犫犲犪犿犻狊犱犲狋犲狉犻狅狉犪狋犲犱犫狅狋犺犻狀狋犺犲狋犲犿狆狅狉犪犾犪狀犱狊狆犪狋犻犪犾犱狅犿犪犻狀狊．犓犲狔狑狅狉犱狊　犱犻犳犳狉犪犮狋犻狅狀犪狀犱犵狉犪狋犻狀犵；犱犻犳犳狉犪犮狋犻狏犲犮犺犪狉犪犮狋犲狉犻狊狋犻犮狊狅犳狏狅犾狌犿犲犵狉犪狋犻狀犵；犮狅狌狆犾犲犱狑犪狏犲狋犺犲狅狉狔；狌犾狋狉犪狊犺狅狉狋狆狌犾狊犲犱犌犪狌狊狊犻犪狀犾犪狊犲狉犫犲犪犿；犉狅狌狉犻犲狉狋狉犪狀狊犳狅狉犿１　引　　言体光栅是一种非常重要的光学元器件，其突出特点是当入射光束满足布拉格条件时具有很高的衍射效率（在某些特殊记录基质中，如光热折变玻璃，其衍射效率可达９９％）以及较好的波长、角度选择性（半高光谱宽度和半高角谱宽度分别可达１００ｐｍ　　收稿日期：２００８０５０６；收到修改稿日期：２００８０７０３基金项目：国家自然科学基金（１０６７６０３８）资助课题。作者简介：郑光威（１９８１－），男，博士研究生，主要从事高功率激光空间低通滤波研究。Ｅｍａｉｌ：ｚｇｗ１９８１９６＠１２６．ｃｏｍ导师简介：谭吉春（１９４７－），男，教授，博士生导师，主要从事光信息获取、传输与处理等方面的研究。Ｅｍａｉｌ：ｎｕｄｔ２００４＠１２６．ｃｏｍ

１期郑光威等：　透射型体光栅对超短脉冲高斯光束衍射特性研究７２１和１００μｒａｄ）［１］。其应用范围主要涉及光束偏转、光束合成以及光束整形等领域［１，２］。与介电常数的峰值犱、Λ、φ分别表示体光栅厚度、周期以及光栅条纹与犣轴的夹角，犓＝２π／Λ。对体光栅衍射特性的理论研究一直是个热门课题。国外Ｋｏｇｅｌｎｉｋ［３］通过一定近似，得出分析体光栅衍射特性的一维耦合波理论，随后Ｓｏｌｙｍｅｒ［４］提出二维、三维耦合波理论，Ｇａｙｌｏｒｄ［５，６］课题组提出严格耦合波理论，车诺夫［７］提出严格三维矢量特征波理论，但他们只分析体光栅对单色平面波的衍射特性，并没有考虑到脉冲高斯光束输入时的一般情况；国内研究有单独考虑高斯光束［８］或超短脉冲激光光束入射至体光栅的衍射特性分析［９，１０］，而分析体光栅对超短脉冲高斯光束的衍射特性方法显得比较复杂［１１］，因此如何有效地分析体光栅对超短脉冲高斯光束的衍射特性就显得非常迫切。本文采用傅里叶频谱以及Ｋｏｇｅｌｎｉｋ耦合波理论，分析超短脉冲高斯光束斜入射至透射型体光栅时的衍射特性，所得结果对实际应用透射型体光栅来完成超短脉冲高斯光束非相干合成、超短脉冲高斯光束偏转以及超短脉冲高斯光束空间低通滤波具有理论指导意义。２　超短脉冲高斯光束的数学描述及其傅里叶展开超短脉冲高斯光束入射至透射型体光栅如图１所示。其中犡犗犣平面为体光栅前表面法向方向犖与光栅矢量犓所在平面，坐标系犡′犢′犣′犗与坐标系犡犢犣犗的对应关系可由角β１和角β２来描述，其中β１表示犢′轴与犢轴之间的夹角，而β２表示犡′轴与犡轴之间的夹角。光栅为传导率和介电常数均正弦同周期变化的体光栅，图１中所示平行条纹表示传导率图１超短脉冲高斯光束入射至透射型体光栅示意图（空域）Ｆｉｇ．１ＳｃｈｅｍａｔｉｃｏｆｉｎｐｕｔｏｆｕｌｔｒａｓｈｏｒｔＧａｕｓｓｉａｎｌａｓｅｒｂｅａｍｉｎｔｏｔｒａｎｓｍｉｔｔｉｎｇｖｏｌｕｍｅｇｒａｔｉｎｇ（ｉｎｓｐａｔｉａｌｄｏｍａｉｎ）为方便讨论，选取平行平面共焦腔基模超短脉冲高斯光束作为研究对象，其电场振幅的标量表达式（忽略电场的相位分布，且偏振方向垂直于入射面。）ｅｘｐ（－狋２／犜２）× 犈＝犈０狑０狑（狕′）ｅｘｐ（－狓′２＋狔′２狑２（狕′）ｅｘｐ［ｉ（２π犳０狋＋犽′０·狉′）］，（１）其中狑０、狑（狕′）＝狑０（１＋（狕′／犳）２）１／２分别表示此高斯光束束腰处的腰斑和距束腰为狕′处的腰斑半径，犳表示共焦腔镜的焦距；犳０＝犮／λ０表示的脉冲的中心频率，λ０为中心波长，犮为真空中的光速；犜＝ Δτ／（２ｌｎ２）１／２，Δτ为高斯脉冲强度分布的脉冲半峰全宽；犽′０表示此光束的中心波矢（方向为光束轴向方向，波数犽０′＝２π／λ０）。利用傅里叶变换，在时域和空域（对在犡′犗犢′ 面内的光场）对（１）式分别作一维以及二维傅里叶展开，其单色单角谱振幅的表达式如下：｛犝（′犽狓，′犽狔，λ，狕′）＝犃ｅｘｐ－（′犽狓－ ′犽狓０））狑（狕′）｛［狑（狕′）［）狕′ ，ｅｘｐ｛－［π犜犮（１／λ－１／λ０）］２｝ｅｘｐｉ′犽狕０（２－′犽狔］２＋２２（２）２）１／２分别表示波矢犽′在犡′轴、犢′轴以及犣′轴上的投影，′犽狓０、′犽狔０和 ′犽狕０分｝２｝］） ·　　　　（′犽狔－ ′犽狔０其中 ′犽狓、′犽狔和 ′犽狕＝（′犽２－′犽狓别表示中心波矢 ′犽０在轴犡′和犢′以及犣′上的投影。由坐标系犡犢犣犗与坐标系犡′犢′犣′犗的对应关系，可得燄 ′犽狓熿 ′犽狔ｃｏｓβ２ｓｉｎβ１ｓｉｎβ２－ｃｏｓβ１ｓｉｎβ２熿燄＝０ｃｏｓβ１ｓｉｎβ１燄犽狓熿犽狔，（３）燀 ′犽燅狕燀ｓｉｎβ２－ｓｉｎβ１ｃｏｓβ２ｃｏｓβ１ｃｏｓβ 燅２燀犽燅狕其中犽狓、犽狔和犽狕分别表示波矢犽在犡轴、犢轴以及犣轴上的投影值。将（３）式代入（２）式即可得出犝（犽狓，犽狔，λ，狕）的大小。定义为波矢犽在犡犗犣平面内的投影犽狓狕与光栅条纹之间的夹角，如图２所示。其表达式如下： ＝ａｒｃｔａｎ（犽狓／犽狕）－φ　　　　狓－犽２＝ａｒｃｔａｎ犽狓／犽２－犽２槡（）狔－φ．（４）

８２１光　　　学　　　学　　　报２９卷　　图２中，ｓ为衍射光束波矢犽ｓ在犡犗犣平面内的投影犽ｓｘｚ与光栅条纹之间的夹角。当波矢犽满足布拉格条件时，犽ｘｚ、犽ｓｘｚ与光栅波矢犓构成封闭三角形。将（４）式代入犝（犽狓，犽狔，λ，狕）即可得到单色单角谱的强度由自变量 、犽狔以及λ 的表示形式犝（，犽狔，λ，狕）。定义超短脉冲高斯光束角谱宽度 ΔＬ（λ＝λ０）和光谱宽度 ΔλＬ（＝０）分别满足下面表达式犝（０＋Δ犔／２，犽狔０，λ０，狕）＝犝（０，犽狔０，λ０，狕）／槡２，（５）犝（０，犽狔０，λ０＋Δλ犔／２，狕）＝犝（０，犽狔０，λ０，狕）／槡２．（６）图２犽ｘｚ、犽ｓｘｚ与犓的矢量关系图Ｆｉｇ．２Ｖｅｃｔｏｒｄｉａｇｒａｍｏｆ犽ｘｚ，犽ｓｘｚ，ａｎｄ犓３　耦合波理论忽略各单色单角谱成分通过体光栅时相互之间的能量耦合，采用类似Ｋｏｇｅｌｎｉｋ耦合波理论的方法，并考虑中心波矢犽０在ＸＯＺ面内且满足布拉格条件，即２ｓｉｎ０犽０＝犓时（此时犽０狓／犽０狕＝ｔａｎ（０＋φ），如图２所示），可得入射光波与衍射光波的耦合波方程组如下：ｄ犚（，犽狔，λ，狕）＋α犚（，犽狔，λ，狕）＋ｉκ犛（犽狊狓，犽狊狔，λ，狕）＝０，烄犆犚烅犆犛烆ｄ犛（犽狊狓，犽狊狔，λ，狕）ｄ狕ｄ狕＋（α＋ｉ）犛（犽狊狓，犽狊狔，λ，狕）＋ｉκ犚（，犽狔，λ，狕）＝０，（７）其中犚（，犽狔，λ，狕）、犛（犽狊狓，犽狊狔，λ，狕）分别表示角谱为（，犽狔）、（犽狊狓，犽狊狔）波长为λ的入射光波以及衍射光波在狕）狔＝－φ，犽狊狔＝犽狔，犆犛＝ｃｏｓ（＋φ）＋犓ｓｉｎφ／β，犆犚＝ｃｏｓ（＋处的振幅，其中：ｔａｎ犽狊狓／犽２－犽２狊狓－犽２槡（狊 φ），β ＝ ω［με０ε狉０（λ）］１／２， ＝犓ｓｉｎ －犓２／２β，α ＝ σ０（λ）［μ／ε０（λ）ε狉０（λ）］１／２／２，κ ＝ ε狉１（λ）β ４ε狉０（λ）＋ σ１（λ）ｉ４［μ／ε０（λ）ε狉０（λ）］１／２，其中ε０、ε狉０（λ）和ε狉１（λ）分别表示自由空间中的介电常数、体光栅中的相对平均介电常数以及介电常数调制度；σ０（λ）、σ１（λ）表示电导率以及电导率的调制度；利用透射型体光栅的边界条件犚（，犽狔，λ，０）＝犝（，犽狔，λ，０）犛（犽狊狓，犽狊狔，λ，狕）＝，可得出衍射光波的复振幅解为：｛０其中ν＝ κ犱（犆犚犆犛）１／２，ξ＝ｉ犆（）犛犛（犽狊狓，犽狊狔，λ，犱）＝－ｉ犝（，犽狔，λ，０）犆犚，Φ＝（ν２＋ξ －ｉ－犱２（ α 犆犚  犆）犛 α 犆犛１／２２）１／２。ｅｘｐ－ｉξ－（ α犱犆）犚ｓｉｎΦ Φ／ν ，（８）由于使用体相位型光栅较体振幅型光栅或混合型光栅的场合要频繁，因此忽略材料的吸收，只考虑体相位型光栅，且光栅无倾斜，即φ＝０°时的情形，可得出衍射光波的强度如下：２）１／２／（１＋ξ （９）　　定义单色单角谱成分的衍射效率为其衍射强度与其入射强度的比值。由（９）式，可得出单色单角谱成分的衍射效率为犐犛（犽狊狓，犽狊狔，λ，犱）＝犝（，犽狔，λ，０）２ｓｉｎ２（ν２＋ξ ２／ν２）， η（犽狊狓，犽狊狔，λ，犱）＝ｓｉｎ２（ν２＋ξ ２）１／２／（１＋ξ ２／ν２），其中狀１（λ）表示折射率调制度，其值等于ε狉１ ν＝ π狀１（λ）犱／（λｃｏｓ）（λ）／［２ ε狉０（λ槡）］。考虑波长和角度失配对衍射效率的影响，对ξ在（φ０，λ０）做一阶泰勒级数展开，可得（１０）（１１） ξ＝犱２犓（［ｃｏｓ２０－犓２４π λ 狀０（λ）ｓｉｎ０ｃｏｓ２ ）０ ·（－０）＋犓２４πｃｏｓ０ ′ λ 狀０（λ（））（λ－λ０］）． λ－λ０（１２）

１期郑光威等：　透射型体光栅对超短脉冲高斯光束衍射特性研究９２１　　狀０（λ）表示平均折射率，其值等于 ε狉０（λ槡）。显然，超短脉冲高斯光束中心波矢分量集中了光束中的大部分的能量，因此当中心波矢成分的衍射效率η（犽狊狓０，犽狊狔０，λ０，犱）＝１时，体光栅对此光束的衍射效率最高。由式（１０）、（１１）和（１２），可得出此式：（１３）　　定义体光栅衍射光强的角谱宽度 ΔＧ和光谱宽度 ΔλＧ分别为其各自主瓣宽度的一半，由（１２）式可推得它们表达式分别为： ν＝ π狀１（λ）犱／（λ０ｃｏｓ０）＝ π（１＋犿）／２　（犿＝０，１，２，３…）． ΔＧ＝槡３π 犱（ · 犓ｃｏｓ２０－犓２４π λ０狀０（λ０）－１ｓｉｎ０ｃｏｓ２ ）０＝槡３π 犓犱＝槡３Λ ２犱， ΔλＧ＝燅０综上，衍射光束在波长为λｐ处为的空域光强，分布为： λ＝λ 燀槡４３π２ｃｏｓφ０熿犓２犱 ′ λ 狀０（）（）λ －１燄＝槡３ｃｏｓ０Λ２犱熿燀 ′ λ 狀０（λ（））－１燄． λ＝λ 燅０犐犱（狓，狔，λｐ）＝ 犛（犽狊狓，犽狊狔，λｐ，犱）·ｅｘｐ［ｉ（犽狊狓＋犽狊狔狔）］ｄ犽狊狓ｄ犽狊狔２而衍射光束在角为（犽狊狓，犽狊狔）处的时域光强分布为：犐狋（狋，犽狊狓，犽狊狔）＝∫犐ｓ（犽狊狓，犽狊狔，λ，犱）（－犮／λ２）ｅｘｐ（犻狕犮狋／λ）ｄλ （１４）（１５）（１６）（１７）４　数值模拟分析当此超短脉冲高斯光束的中心波矢犽０满足体光栅的布拉格条件时，衍射光束在时域波形以及空域在光栅矢量犓方向上的分布（因为一维体光栅仅对平行于光栅波矢方向的分量有衍射作用）随体光栅周期以及厚度的变化规律。对于下面的模拟过程，均假定：ⅰ）光栅为各向同性介质，且忽略光栅的色散特性，在此超短脉冲光谱范围内狀０（λ）＝１．５００；ⅱ）满足体光栅条件（犙＝２πλ犱／［（狀０（λ）Λ２］＞１［１２］）；（ⅲ）超短脉冲高斯光束的中心波长λ０＝１０６４ｎｍ，脉宽犜＝１００ｆｓ，束腰半径狑（０）＝０．２５ｍｍ。由（５）、（６）式，可以得出光谱宽度 ΔλＬ＝２８ｎｍ和角谱宽度 ΔＬ＝２．０ｍｒａｄ。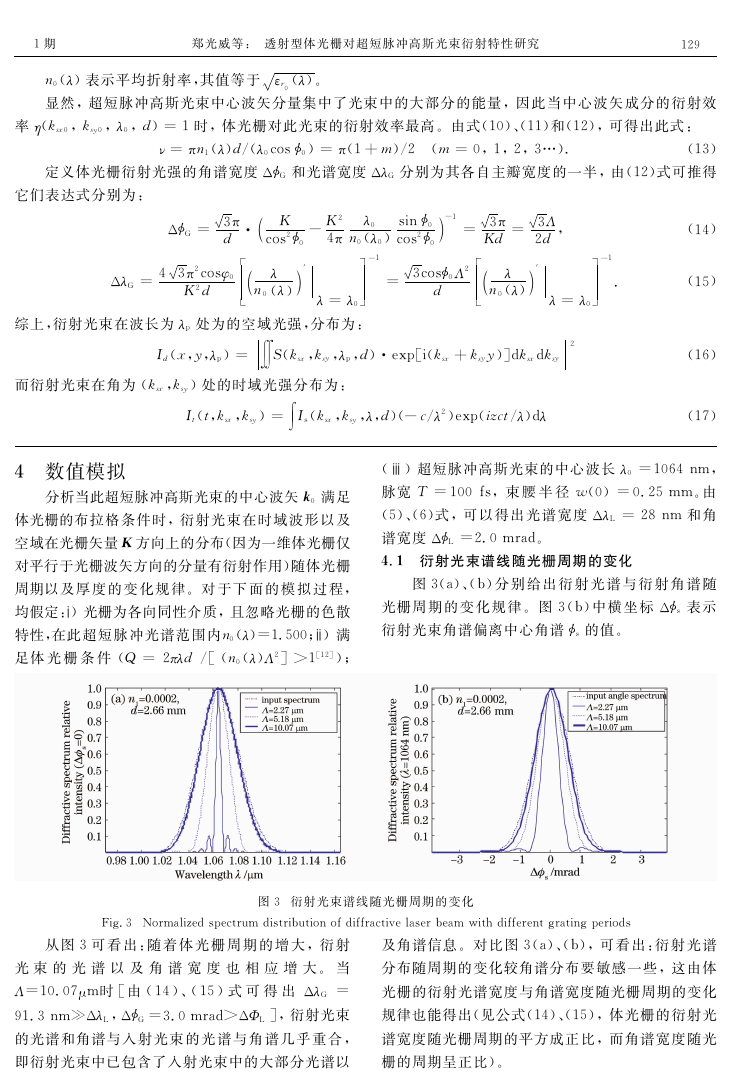４．１　衍射光束谱线随光栅周期的变化图３（ａ）、（ｂ）分别给出衍射光谱与衍射角谱随光栅周期的变化规律。图３（ｂ）中横坐标 Δｓ表示衍射光束角谱偏离中心角谱ｓ的值。图３衍射光束谱线随光栅周期的变化Ｆｉｇ．３Ｎｏｒｍａｌｉｚｅｄｓｐｅｃｔｒｕｍｄｉｓｔｒｉｂｕｔｉｏｎｏｆｄｉｆｆｒａｃｔｉｖｅｌａｓｅｒｂｅａｍｗｉｔｈｄｉｆｆｅｒｅｎｔｇｒａｔｉｎｇｐｅｒｉｏｄｓ　　从图３可看出：随着体光栅周期的增大，衍射光束的光谱以及角谱宽度也相应增大。当 Λ＝１０．０７μｍ时［由（１４）、（１５）式可得出 ΔλＧ＝９１．３ｎｍΔλＬ，ΔＧ＝３．０ｍｒａｄ＞ΔΦＬ］，衍射光束的光谱和角谱与入射光束的光谱与角谱几乎重合，及角谱信息。对比图３（ａ）、（ｂ），可看出：衍射光谱分布随周期的变化较角谱分布要敏感一些，这由体光栅的衍射光谱宽度与角谱宽度随光栅周期的变化规律也能得出（见公式（１４）、（１５），体光栅的衍射光谱宽度随光栅周期的平方成正比，而角谱宽度随光即衍射光束中已包含了入射光束中的大部分光谱以栅的周期呈正比）。

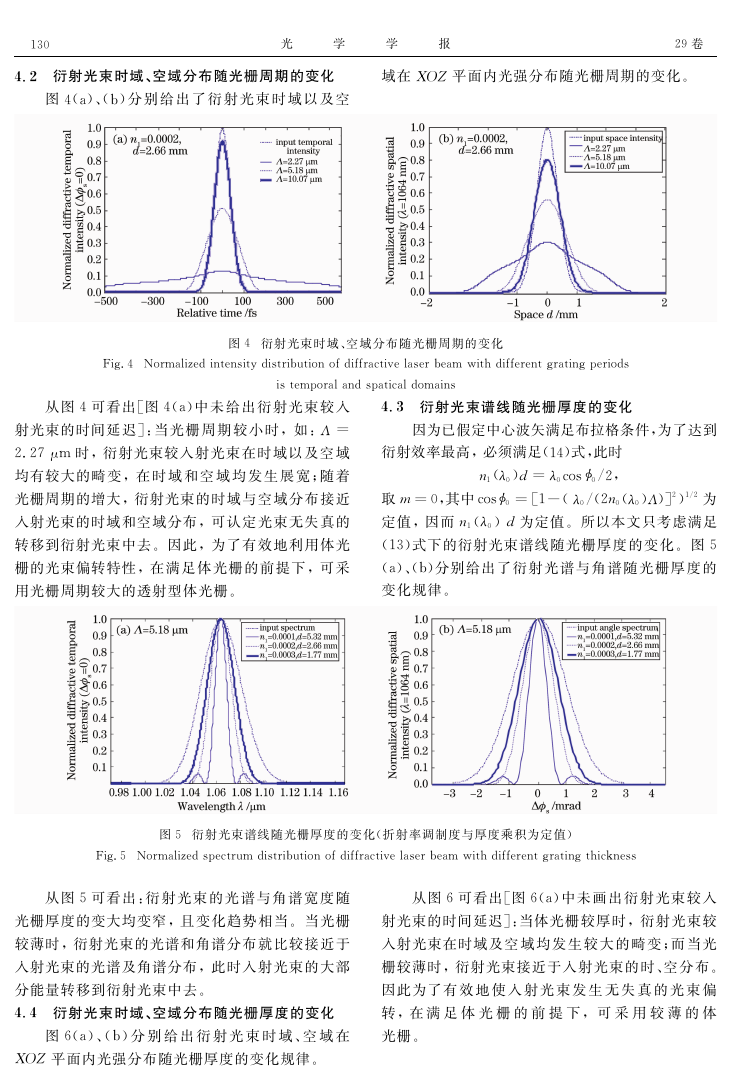
０３１光　　　学　　　学　　　报２９卷４．２　衍射光束时域、空域分布随光栅周期的变化域在犡犗犣平面内光强分布随光栅周期的变化。图４（ａ）、（ｂ）分别给出了衍射光束时域以及空图４衍射光束时域、空域分布随光栅周期的变化Ｆｉｇ．４Ｎｏｒｍａｌｉｚｅｄｉｎｔｅｎｓｉｔｙｄｉｓｔｒｉｂｕｔｉｏｎｏｆｄｉｆｆｒａｃｔｉｖｅｌａｓｅｒｂｅａｍｗｉｔｈｄｉｆｆｅｒｅｎｔｇｒａｔｉｎｇｐｅｒｉｏｄｓｉｓｔｅｍｐｏｒａｌａｎｄｓｐａｔｉｃａｌｄｏｍａｉｎｓ　　从图４可看出［图４（ａ）中未给出衍射光束较入射光束的时间延迟］：当光栅周期较小时，如：Λ ＝２．２７μｍ时，衍射光束较入射光束在时域以及空域均有较大的畸变，在时域和空域均发生展宽；随着光栅周期的增大，衍射光束的时域与空域分布接近入射光束的时域和空域分布，可认定光束无失真的转移到衍射光束中去。因此，为了有效地利用体光栅的光束偏转特性，在满足体光栅的前提下，可采用光栅周期较大的透射型体光栅。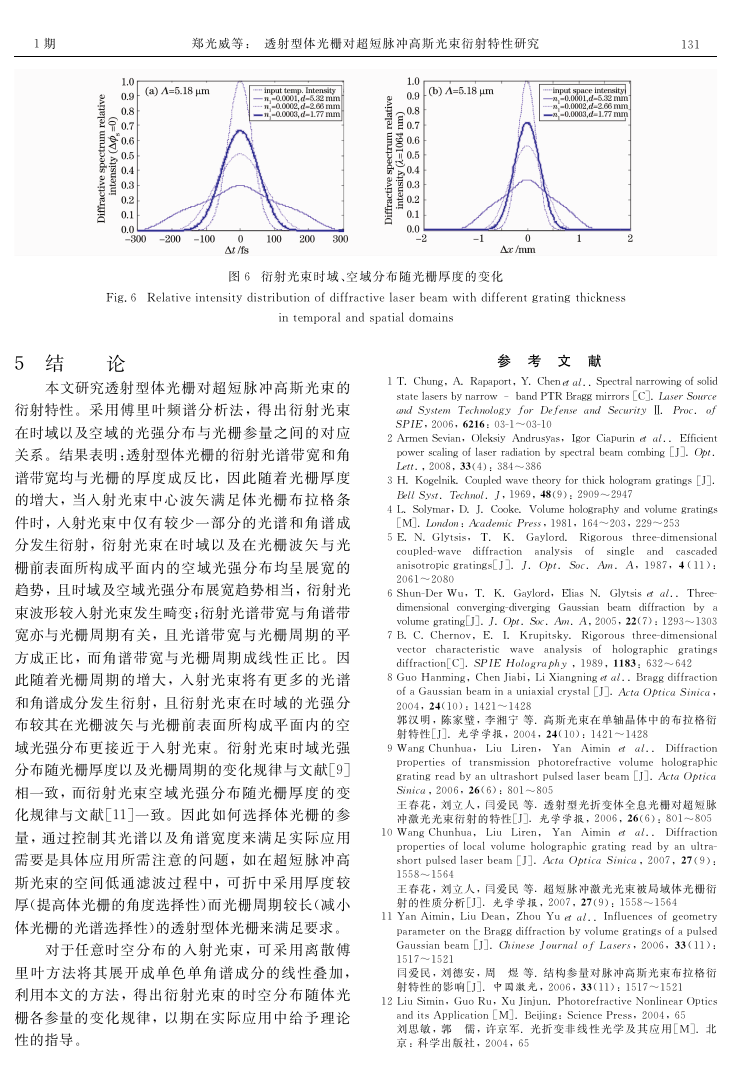４．３　衍射光束谱线随光栅厚度的变化因为已假定中心波矢满足布拉格条件，为了达到衍射效率最高，必须满足（１４）式，此时狀１（λ０）犱＝λ０ｃｏｓ０／２，取犿＝０，其中ｃｏｓ０＝［１－（λ０／（２狀０（λ０）Λ）］２）１／２为定值，因而狀１（λ０）犱为定值。所以本文只考虑满足（１３）式下的衍射光束谱线随光栅厚度的变化。图５（ａ）、（ｂ）分别给出了衍射光谱与角谱随光栅厚度的变化规律。图５衍射光束谱线随光栅厚度的变化（折射率调制度与厚度乘积为定值）Ｆｉｇ．５Ｎｏｒｍａｌｉｚｅｄｓｐｅｃｔｒｕｍｄｉｓｔｒｉｂｕｔｉｏｎｏｆｄｉｆｆｒａｃｔｉｖｅｌａｓｅｒｂｅａｍｗｉｔｈｄｉｆｆｅｒｅｎｔｇｒａｔｉｎｇｔｈｉｃｋｎｅｓｓ　　从图５可看出：衍射光束的光谱与角谱宽度随光栅厚度的变大均变窄，且变化趋势相当。当光栅从图６可看出［图６（ａ）中未画出衍射光束较入射光束的时间延迟］：当体光栅较厚时，衍射光束较较薄时，衍射光束的光谱和角谱分布就比较接近于入射光束在时域及空域均发生较大的畸变；而当光入射光束的光谱及角谱分布，此时入射光束的大部栅较薄时，衍射光束接近于入射光束的时、空分布。分能量转移到衍射光束中去。４．４　衍射光束时域、空域分布随光栅厚度的变化因此为了有效地使入射光束发生无失真的光束偏转，在满足体光栅的前提下，可采用较薄的体图６（ａ）、（ｂ）分别给出衍射光束时域、空域在光栅。犡犗犣平面内光强分布随光栅厚度的变化规律。

１期郑光威等：　透射型体光栅对超短脉冲高斯光束衍射特性研究１３１图６衍射光束时域、空域分布随光栅厚度的变化Ｆｉｇ．６Ｒｅｌａｔｉｖｅｉｎｔｅｎｓｉｔｙｄｉｓｔｒｉｂｕｔｉｏｎｏｆｄｉｆｆｒａｃｔｉｖｅｌａｓｅｒｂｅａｍｗｉｔｈｄｉｆｆｅｒｅｎｔｇｒａｔｉｎｇｔｈｉｃｋｎｅｓｓｉｎｔｅｍｐｏｒａｌａｎｄｓｐａｔｉａｌｄｏｍａｉｎｓ５　结　　论本文研究透射型体光栅对超短脉冲高斯光束的衍射特性。采用傅里叶频谱分析法，得出衍射光束在时域以及空域的光强分布与光栅参量之间的对应关系。结果表明：透射型体光栅的衍射光谱带宽和角谱带宽均与光栅的厚度成反比，因此随着光栅厚度的增大，当入射光束中心波矢满足体光栅布拉格条件时，入射光束中仅有较少一部分的光谱和角谱成分发生衍射，衍射光束在时域以及在光栅波矢与光栅前表面所构成平面内的空域光强分布均呈展宽的趋势，且时域及空域光强分布展宽趋势相当，衍射光束波形较入射光束发生畸变；衍射光谱带宽与角谱带宽亦与光栅周期有关，且光谱带宽与光栅周期的平方成正比，而角谱带宽与光栅周期成线性正比。因此随着光栅周期的增大，入射光束将有更多的光谱和角谱成分发生衍射，且衍射光束在时域的光强分布较其在光栅波矢与光栅前表面所构成平面内的空域光强分布更接近于入射光束。衍射光束时域光强分布随光栅厚度以及光栅周期的变化规律与文献［９］相一致，而衍射光束空域光强分布随光栅厚度的变化规律与文献［１１］一致。因此如何选择体光栅的参量，通过控制其光谱以及角谱宽度来满足实际应用需要是具体应用所需注意的问题，如在超短脉冲高斯光束的空间低通滤波过程中，可折中采用厚度较厚（提高体光栅的角度选择性）而光栅周期较长（减小体光栅的光谱选择性）的透射型体光栅来满足要求。对于任意时空分布的入射光束，可采用离散傅里叶方法将其展开成单色单角谱成分的线性叠加，利用本文的方法，得出衍射光束的时空分布随体光栅各参量的变化规律，以期在实际应用中给予理论性的指导。参考文献１Ｔ．Ｃｈｕｎｇ，Ａ．Ｒａｐａｐｏｒｔ，Ｙ．Ｃｈｅｎ犲狋犪犾．．ＳｐｅｃｔｒａｌｎａｒｒｏｗｉｎｇｏｆｓｏｌｉｄｓｔａｔｅｌａｓｅｒｓｂｙｎａｒｒｏｗｂａｎｄＰＴＲＢｒａｇｇｍｉｒｒｏｒｓ［Ｃ］．犔犪狊犲狉犛狅狌狉犮犲犪狀犱犛狔狊狋犲犿犜犲犮犺狀狅犾狅犵狔犳狅狉犇犲犳犲狀狊犲犪狀犱犛犲犮狌狉犻狋狔 Ⅱ．犘狉狅犮．狅犳犛犘犐犈，２００６，６２１６：０３１～０３１０２ＡｒｍｅｎＳｅｖｉａｎ，ＯｌｅｋｓｉｙＡｎｄｒｕｓｙａｓ，ＩｇｏｒＣｉａｐｕｒｉｎ犲狋犪犾．．Ｅｆｆｉｃｉｅｎｔｐｏｗｅｒｓｃａｌｉｎｇｏｆｌａｓｅｒｒａｄｉａｔｉｏｎｂｙｓｐｅｃｔｒａｌｂｅａｍｃｏｍｂｉｎｇ［Ｊ］．犗狆狋．犔犲狋狋．，２００８，３３（４）：３８４～３８６３Ｈ．Ｋｏｇｅｌｎｉｋ．Ｃｏｕｐｌｅｄｗａｖｅｔｈｅｏｒｙｆｏｒｔｈｉｃｋｈｏｌｏｇｒａｍｇｒａｔｉｎｇｓ［Ｊ］．犅犲犾犾犛狔狊狋．犜犲犮犺狀狅犾．犑，１９６９，４８（９）：２９０９～２９４７４Ｌ．Ｓｏｌｙｍａｒ，Ｄ．Ｊ．Ｃｏｏｋｅ．Ｖｏｌｕｍｅｈｏｌｏｇｒａｐｈｙａｎｄｖｏｌｕｍｅｇｒａｔｉｎｇｓ［Ｍ］．犔狅狀犱狅狀：犃犮犪犱犲犿犻犮犘狉犲狊狊，１９８１，１６４～２０３，２２９～２５３５Ｅ．Ｎ．Ｇｌｙｔｓｉｓ，Ｔ．Ｋ．Ｇａｙｌｏｒｄ．Ｒｉｇｏｒｏｕｓｔｈｒｅｅｄｉｍｅｎｓｉｏｎａｌｃｏｕｐｌｅｄｗａｖｅｄｉｆｆｒａｃｔｉｏｎａｎａｌｙｓｉｓｏｆｓｉｎｇｌｅａｎｄｃａｓｃａｄｅｄａｎｉｓｏｔｒｏｐｉｃｇｒａｔｉｎｇｓ［Ｊ］．犑．犗狆狋．犛狅犮．犃犿．犃，１９８７，４（１１）：２０６１～２０８０６ＳｈｕｎＤｅｒＷｕ，Ｔ．Ｋ．Ｇａｙｌｏｒｄ，ＥｌｉａｓＮ．Ｇｌｙｔｓｉｓ犲狋犪犾．．Ｔｈｒｅｅ ｄｉｍｅｎｓｉｏｎａｌｃｏｎｖｅｒｇｉｎｇｄｉｖｅｒｇｉｎｇＧａｕｓｓｉａｎｂｅａｍｄｉｆｆｒａｃｔｉｏｎｂｙａｖｏｌｕｍｅｇｒａｔｉｎｇ［Ｊ］．犑．犗狆狋．犛狅犮．犃犿．犃，２００５，２２（７）：１２９３～１３０３７Ｂ．Ｃ．Ｃｈｅｒｎｏｖ，Ｅ．Ｉ．Ｋｒｕｐｉｔｓｋｙ．Ｒｉｇｏｒｏｕｓｔｈｒｅｅｄｉｍｅｎｓｉｏｎａｌｖｅｃｔｏｒｃｈａｒａｃｔｅｒｉｓｔｉｃｗａｖｅａｎａｌｙｓｉｓｏｆｈｏｌｏｇｒａｐｈｉｃｇｒａｔｉｎｇｓｄｉｆｆｒａｃｔｉｏｎ［Ｃ］．犛犘犐犈犎狅犾狅犵狉犪狆犺狔，１９８９，１１８３：６３２～６４２８ＧｕｏＨａｎｍｉｎｇ，ＣｈｅｎＪｉａｂｉ，ＬｉＸｉａｎｇｎｉｎｇ犲狋犪犾．．ＢｒａｇｇｄｉｆｆｒａｃｔｉｏｎｏｆａＧａｕｓｓｉａｎｂｅａｍｉｎａｕｎｉａｘｉａｌｃｒｙｓｔａｌ［Ｊ］．犃犮狋犪犗狆狋犻犮犪犛犻狀犻犮犪，２００４，２４（１０）：１４２１～１４２８　郭汉明，陈家璧，李湘宁等．高斯光束在单轴晶体中的布拉格衍射特性［Ｊ］．光学学报，２００４，２４（１０）：１４２１～１４２８９ＷａｎｇＣｈｕｎｈｕａ，ＬｉｕＬｉｒｅｎ，ＹａｎＡｉｍｉｎ犲狋犪犾．．Ｄｉｆｆｒａｃｔｉｏｎｐｒｏｐｅｒｔｉｅｓｏｆｔｒａｎｓｍｉｓｓｉｏｎｐｈｏｔｏｒｅｆｒａｃｔｉｖｅｖｏｌｕｍｅｈｏｌｏｇｒａｐｈｉｃｇｒａｔｉｎｇｒｅａｄｂｙａｎｕｌｔｒａｓｈｏｒｔｐｕｌｓｅｄｌａｓｅｒｂｅａｍ［Ｊ］．犃犮狋犪犗狆狋犻犮犪犛犻狀犻犮犪，２００６，２６（６）：８０１～８０５　王春花，刘立人，闫爱民等．透射型光折变体全息光栅对超短脉冲激光光束衍射的特性［Ｊ］．光学学报，２００６，２６（６）：８０１～８０５１０ＷａｎｇＣｈｕｎｈｕａ，ＬｉｕＬｉｒｅｎ，ＹａｎＡｉｍｉｎ犲狋犪犾．．Ｄｉｆｆｒａｃｔｉｏｎｐｒｏｐｅｒｔｉｅｓｏｆｌｏｃａｌｖｏｌｕｍｅｈｏｌｏｇｒａｐｈｉｃｇｒａｔｉｎｇｒｅａｄｂｙａｎｕｌｔｒａ ｓｈｏｒｔｐｕｌｓｅｄｌａｓｅｒｂｅａｍ［Ｊ］．犃犮狋犪犗狆狋犻犮犪犛犻狀犻犮犪，２００７，２７（９）：１５５８～１５６４　王春花，刘立人，闫爱民等．超短脉冲激光光束被局域体光栅衍射的性质分析［Ｊ］．光学学报，２００７，２７（９）：１５５８～１５６４１１ＹａｎＡｉｍｉｎ，ＬｉｕＤｅａｎ，ＺｈｏｕＹｕ犲狋犪犾．．ＩｎｆｌｕｅｎｃｅｓｏｆｇｅｏｍｅｔｒｙｐａｒａｍｅｔｅｒｏｎｔｈｅＢｒａｇｇｄｉｆｆｒａｃｔｉｏｎｂｙｖｏｌｕｍｅｇｒａｔｉｎｇｓｏｆａｐｕｌｓｅｄＧａｕｓｓｉａｎｂｅａｍ［Ｊ］．犆犺犻狀犲狊犲犑狅狌狉狀犪犾狅犳犔犪狊犲狉狊，２００６，３３（１１）：１５１７～１５２１　闫爱民，刘德安，周　煜等．结构参量对脉冲高斯光束布拉格衍射特性的影响［Ｊ］．中国激光，２００６，３３（１１）：１５１７～１５２１１２ＬｉｕＳｉｍｉｎ，ＧｕｏＲｕ，ＸｕＪｉｎｊｕｎ．ＰｈｏｔｏｒｅｆｒａｃｔｉｖｅＮｏｎｌｉｎｅａｒＯｐｔｉｃｓａｎｄｉｔｓＡｐｐｌｉｃａｔｉｏｎ［Ｍ］．Ｂｅｉｊｉｎｇ：ＳｃｉｅｎｃｅＰｒｅｓｓ，２００４，６５　刘思敏，郭　儒，许京军．光折变非线性光学及其应用［Ｍ］．北京：科学出版社，２００４，６５

分享到：

赞收藏

资料库

透射型体光栅对超短脉冲高斯光束衍射特性研究.pdf

相关推荐

开发技术

热门标签

最新资料