logo资料库

论文研究-基于改进粒子群算法的认知无线电频谱分配 .pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.35M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 基于改进粒子群算法的认知无线电频谱分 配 5 10 乔思宁，孙学斌，周正** （北京邮电大学信息与通信工程学院，北京 100876） 摘要：在认知无线电系统中，频谱分配技术是是有效利用有限频谱资源的关键，本文以最大 化系统效益为目标，提出了一种基于改进粒子群算法的认知无线电频谱分配策略。传统二进 制粒子群算法具有初期收敛过快，而在后期容易陷入早熟，局部最优解的缺点。本文根据这 一情况提出了混沌初始化种群，保证了初始粒子在解空间的均匀分布，并修改了传统二进制 粒子群的位置更新策略。通过实验证明，新的算法具有较快的收敛速度和收敛精度,并且有 效的解决了早熟收敛，陷入局部最优解的问题，得到的最大化系统效益值更高。 关键词：认知无线电；频谱分配；混沌初始化；二进制粒子群算法 中图分类号：TN911.7 15 Cognitive Radio Spectrum Allocation Strategy Based on Improved Particle Swarm Optimization QIAO Sining, SUN Xuebin, ZHOU Zheng (School of Information and Communication Engineering, Beijing 100876) 20 25 30 Abstract: Spectrum allocation technology is key of effectively utilizing the limited spectrum resources in the cognitive radio system. For maximizing the system efficiency, this paper brings forward a cognitive radio sepctrum allocation strategy based on improved particle swarm optimization. The original particle swarm optimization has a weakness of easy initial-convergence and easy falling into early-maturing so that it can't get out of a locally optimal solution. Accoding to these situations, this paper comes up with a population initiation based on Chaos. This solution can guarantee the uniform distribution of the initial particles. Also, this paper has alterd the particle's location updating strategey. The experimental results show show that the new improved algorithm has a quicker convergence speed and higher convergence precision. The new algorithm solved the problem of early-maturing convergence and locally optimal solution. The new algorithm can get higher system efficiency. Key words: cognitive radio; spectrum allocation; chaos initiation; binary particle swarm optimization 0 引言 35 随着无线用户的数量急剧增加，导致频谱资源变得越来越稀缺。为了解决频谱资源日益 紧张和由于固定频谱分配造成的频谱利用率低的问题， 在软件无线电的基础上提出了认知 无线电[1]的概念。为了提高频谱利用率，同时降低系统功率损耗，需要提出新的认知无线电 频谱分配算法。目前研究的基于智能算法的认知无线电分配算法有粒子群优化算法[2]（PSO， Particle Swarm Optimization），简单遗传算法[3] (SGA, Simple Genetic Algorithm)，量子遗传 算法[4] (QGA, Quantum Genetic Algorithm),自适应遗传算法[5] (SAGA, Self-adaptive Genetic Algorithm )等。文献[3]将遗传算法(SGA)应用于认知无线电频谱分配中, 但是该算法存在收 40 敛速度慢、早熟等问题, 导致优化的效率较低，不能很好地适应复杂多变的认知环境。文献 作者简介：乔思宁（1990-），男，硕士，主要研究方向：无线通信新技术 通信联系人：周正（1945-），男，教授，博士生导师，主要研究方向:信号处理、无线通信技术. E-mail: zzhou@bupt.edu.cn - 1 -
    中国科技论文在线 http://www.paper.edu.cn [6]中介绍了二进制粒子群算法(BPSO,Binary Particle Swarm Optimization)，在收敛速度上有一 定的提高，但也容易陷入局部最优。 45 初始群体是粒子群算法搜索寻优的出发点，初始群体的构造关系着算法的执行效率。在 初始群体的构造过程中需要保证初始群体的多样性，避免算法陷入局部收敛。由于群体是个 体构成的，因而，如果产生的个体能够遍布整个搜索空间，就能在一定程度上保证初始群体 的多样性。在目前的基于粒子群的认知无线电算法中，并没有在种群的初始化进行改进，本 文针对这一点, 提出了一种结合混沌映射的新的粒子群算法，并对粒子群算法的位置更新策 50 略进行了改进，最后通过仿真比较了本文算法与传统粒子群算法以及自适应遗传算法在认知 无线电频谱分配应用，验证了本文算法的可行性和优越性。 1 改进粒子群算法 1.1 场景描述及建模 认知无线电的频谱分配模型可用频谱矩阵、效益矩阵、干扰矩阵和无干扰分配矩阵来描 55 述[7]。假设在一个分配周期内，频谱环境变化不变（即分配周期相对环境变化来说很短）， 因此在分配周期内各矩阵将保持不变。现实场景可以模拟为一个二维平面，在该区域内主用 户数为 M 随机分布在该区域内各点上，认知用户数为 N 同样随机分布在该区域内任意位置。 可用频谱数与主用户数保持相等，并且各主用户使用的频段各不相同。主用户在使用频段上 有一个保护半径 ，在该范围内不允许有其他感知用户使用该频段，否则会干扰到主用户。 60 认知用户的发射半径在 区间内， 表示认知用户最小的发射半径， 表示 允许的最大发射半径。各有关的矩阵定义如下： 1）空闲矩阵 L。 ， ，则表示频段 m 对认知用户 n 是可用的。如果 ，则 ，否则 。其中 表示认知用户允 许使用频段 m 的覆盖半径，其计算公式如下： 65 （1） 其中， 表示认知用户的位置， 表示主用户的位置， ，表示他们之 间的距离。 2）效益矩阵 B。 ， 代表认知用户 n 使用频段 m 所带来的收益。本 论文的效益 指的是认知用户 n 使用频段 m 所能覆盖的最大范围，覆盖得越广效益越大。 70 其计算表达式为： （2） 3）干扰矩阵 C。 ，如果 =1，则表示认知用户 n 和认知用户 k 在同时使用频段 m 的时候会产生干扰。 如果 则 =1，否则 =0。 75 4）无干扰分配矩阵 A。 ， =1，表示频带 m 分配给了 认知用户 n。A 中的元素必须满足 C 定义的无干扰条件： - 2 - PRDminmax[d,d]mindmaxd,,{l|}01l,nmnmNML,1nmlmin(n,m)dsd,0nml,1nml(n,m)sdmax1...,(n,m)min(d,min{DIST(,x)})kskKymnkPRdDnxkDIST(,x)nk,{b}nmNMB,bnm,bnm2,(n,m)nmsbd,,,,{c|c{0,1}}nkmnkmNNMC,,cnkm(n,m)(k,m)DIST(,)ssnkdd,,cnkm,,cnkm,|,|{a|a{0,1}}nmnmNMA,|anm
    中国科技论文在线 http://www.paper.edu.cn 其中 ，满足式（1）的矩阵 A 有很多，频谱分配算法就是要根据一 （3） 定的分配目标和准则，寻找到使目标值最优的分配矩阵。 80 本论文所采用的目标函数为总带宽收益： （4） U 越大，该分配得到的带宽收益越大。 1.2 粒子群算法 粒子群算法于 1995 年提出[8-9]，PSO 算法将每个个体视为 D 维搜索空间中的一个没有 体积和质量的粒子。该粒子具有自学习和社会学习的能力。通过每个粒子对自身速度和位置 85 的逐代更新，最终整个种群在搜索空间中找到全局最优解。 假设某种群中有 I 个粒子，第 i 个粒子在 D 维空间的第 k 次迭代后速度和位置分别表示 为 和 。粒子的速度和位置更新公式为： 90 （5） （6） 式中：w 是惯性权重，体现了速度本身的记忆性； ， 分别是自学习因子和社会学 习因子，为使算法收敛；0< , <2； ， 是 2 个介于[0,1]之间服从均匀分布的随机数； 粒子 i 在 d 维第 k 次迭代之后经历过的最优位置由 表示，整个种群在 d 维第 k 次迭代之 后经历过的最优位置为 。 95 为了解决离散空间中目标优化的问题，PSO 算法的离散二进制形式 BPSO 被提出[10]。 该算法的速度更新公式不变,如式(5)所示。但其位置由于被离散化为 0 和 1，相应的更新公 式做了以下调整： 式中： 是介于[0,1]之间服从均匀分布的随机数， 为将连续取值的速度离散为 （7） 100 0 或 1 的 Sigmoid 函数。 1.3 种群初始化改进 （8） 研究表明，粒子群初始化对算法的性能产生一定的影响，在以往的基本粒子群初始化过 程是随机的,Richards[11]等提出应尽可能的将粒子均匀初始化在解空间中，如果初始种群比较 好，将会有助于求解效率与解的质量。利用混沌具有不重复的遍历性和伪随机特性初始化粒 105 子的位置和速度，提高种群的多样性，本文采用混沌 Logistic 映射，其定义如下： （9） - 3 - ,,,,a01nmkmnkmac0,,0nkNmM,,11abNMnmnmnmU12[,,...,]kkkkiiiiDxxxx12[v,v,...,v]kkkkiiiiDV+11122+c()c()kkkkkkididididgdidwrrvvpxpx1+1kkkidididxxv1c2c1c2c1r2rkidpkgdp+1+11,
    中国科技论文在线 http://www.paper.edu.cn 式中 为实值序列， 为混沌因子，研究表明，当 3.571448 4 时，该混沌映射处于 混沌状态，在某一初始化条件 下，由 Logistic 映射成序列为 ，具有混沌 110 序 列 特 性 。 本 文 中 设 置 =4 ， 初 始 随 机 产 生 D 维区 间 为 [0,1]的 随 机 数 =Rnd() ， ，D 维长度值为 L 矩阵行数与列数的乘积 N M。在此基础上采用 Logistic 系统进行 N-1 次混沌映射 ，最后需要将种群重 新恢复成 0,1 取值的序列，本文采用的是四舍五入的方法大于 0.5 的取值为 1，反之取值为 0。 1.4 种群位置更新改进 115 由 J. Kennedy 和 R. Eberhart 开发出来的离散二进制 PSO 算法的速度更新公式与原始 PSO 算法一样，但是位置更新采用本文式（7），式（8）。需要注意的是 Sigmoid 并不代表 位变化的概率，只是代表某位取 1 的概率。通过分析可以发现当速度接近于 0 的时候，也就 是当粒子越来越靠近全局最优例子的时候，位置的改变概率为 0.5 左右。也就是说粒子与最 优粒子的距离并不是越来越趋近，而是随机的。可以说算法冲某种程度上退化成了一种随机 120 寻找的算法。因此需要对位置更新公式进行进一步的修改。 当速度为 0 的时候需要位改变概率为 0，而速度很大的时候位改变较大。因此 Sigmoid 更改为如下 NewSigmod 函数： 接着需要对粒子位置更新改为如下形式： 125 当 时 当 时 （10） （11） 用（11）（12）代替（7），经过验证会很快收敛于全局点不动。根据之前的分析原始 BPSO 130 算法运行到最后时具有较强的随机性，说明它具有全局搜索能力，不具备局部搜索性。而新 公式恰恰相反。因此本论文把两者进行了结合，使算法早起具备全局搜索能力，后期具备局 部搜索能力。最终位置更新表达式如下： If 算法利用（7）（8）进行计算 135 Else 算法采用（10）（11）进行计算 其中 取值在[0,1]之间，iter 为目前迭代次数，MaxIter 为总迭代次数。当 iter 为 1 时则 为原始 BPSO 位置更新公式。新改进算法暂时命名为 CBPSO（Chaos-init Binary Particle Swarm Optimization）。 - 4 - zk1z{z|k1,2,3,...}k1jz{j1,2,3,...,D}1,,,zz(1z),{i[1,N1],j[1,D]}ijijij21 v0 1exp(v)21 v01exp(v)S(v)idididididv0id0 if rand()s(v) otherwiseidididxxv0id1 if rand()s(v) otherwiseidididxxiterMaxIter
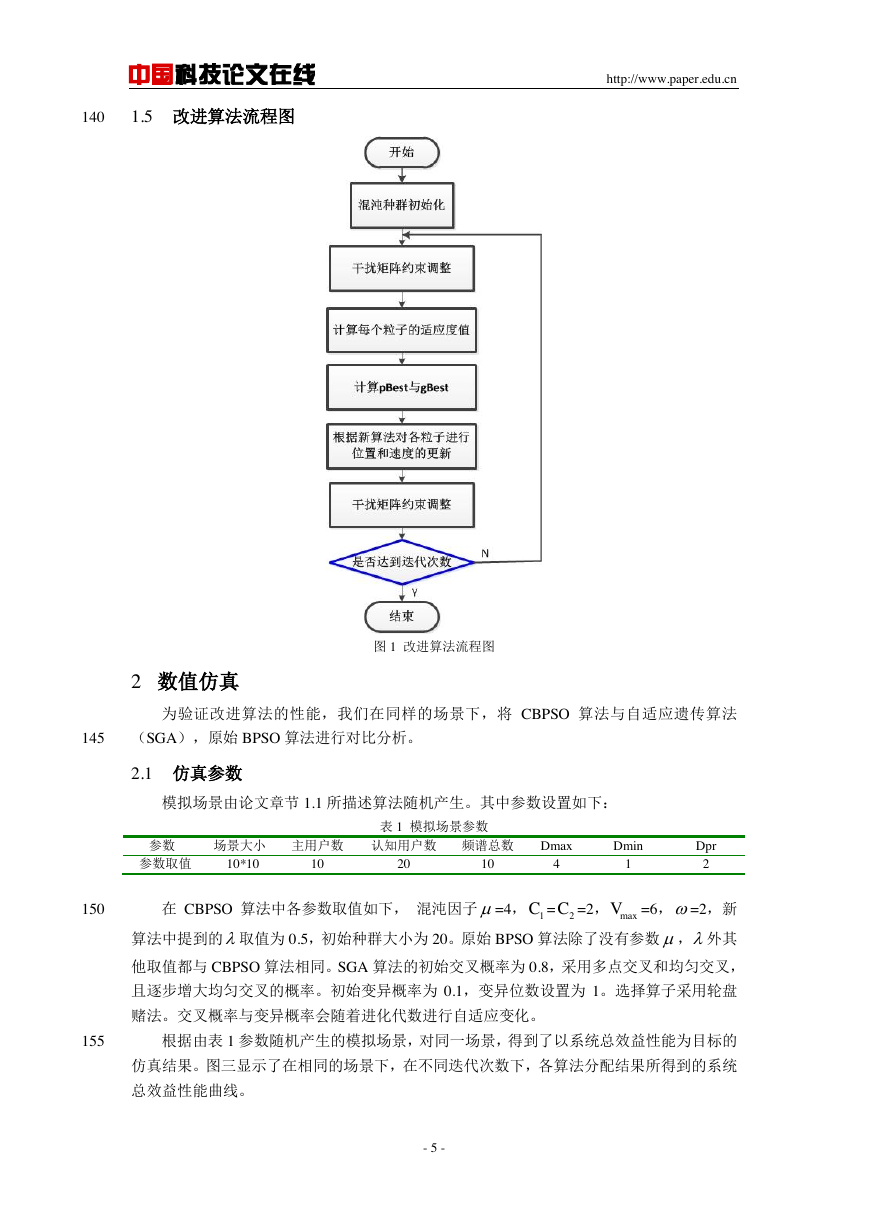
    中国科技论文在线 http://www.paper.edu.cn 140 1.5 改进算法流程图 图 1 改进算法流程图 2 数值仿真 为验证改进算法的性能，我们在同样的场景下，将 CBPSO 算法与自适应遗传算法 145 （SGA），原始 BPSO 算法进行对比分析。 2.1 仿真参数 模拟场景由论文章节 1.1 所描述算法随机产生。其中参数设置如下： 表 1 模拟场景参数 参数 场景大小 主用户数 认知用户数 频谱总数 Dmax 参数取值 10*10 10 20 10 4 Dmin 1 Dpr 2 150 在 CBPSO 算法中各参数取值如下， 混沌因子 =4， = =2， =6， =2，新 算法中提到的 取值为 0.5，初始种群大小为 20。原始 BPSO 算法除了没有参数 ， 外其 他取值都与 CBPSO 算法相同。SGA 算法的初始交叉概率为 0.8，采用多点交叉和均匀交叉， 且逐步增大均匀交叉的概率。初始变异概率为 0.1，变异位数设置为 1。选择算子采用轮盘 赌法。交叉概率与变异概率会随着进化代数进行自适应变化。 155 根据由表 1 参数随机产生的模拟场景，对同一场景，得到了以系统总效益性能为目标的 仿真结果。图三显示了在相同的场景下，在不同迭代次数下，各算法分配结果所得到的系统 总效益性能曲线。 - 5 - 1C2CmaxV
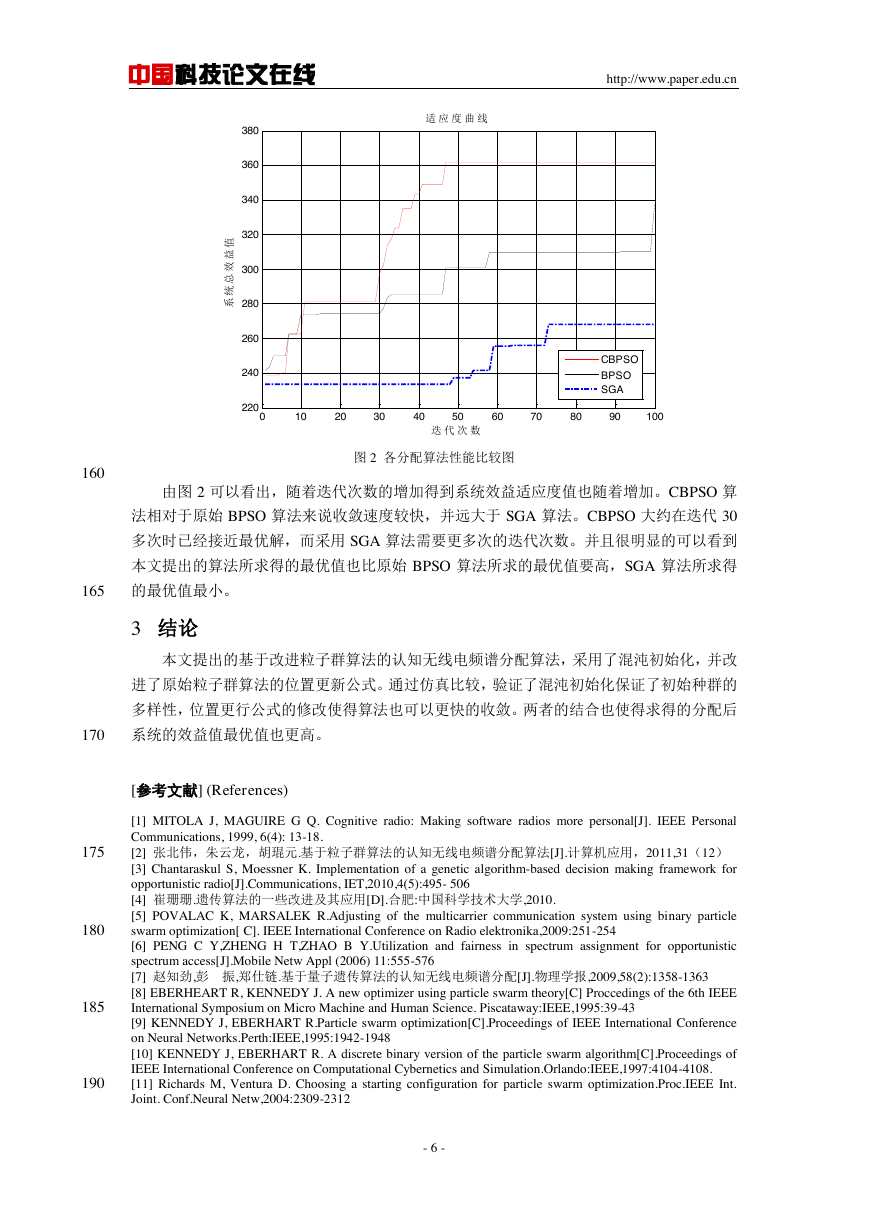
    中国科技论文在线 http://www.paper.edu.cn 160 图 2 各分配算法性能比较图 由图 2 可以看出，随着迭代次数的增加得到系统效益适应度值也随着增加。CBPSO 算 法相对于原始 BPSO 算法来说收敛速度较快，并远大于 SGA 算法。CBPSO 大约在迭代 30 多次时已经接近最优解，而采用 SGA 算法需要更多次的迭代次数。并且很明显的可以看到 本文提出的算法所求得的最优值也比原始 BPSO 算法所求的最优值要高，SGA 算法所求得 165 的最优值最小。 3 结论 本文提出的基于改进粒子群算法的认知无线电频谱分配算法，采用了混沌初始化，并改 进了原始粒子群算法的位置更新公式。通过仿真比较，验证了混沌初始化保证了初始种群的 多样性，位置更行公式的修改使得算法也可以更快的收敛。两者的结合也使得求得的分配后 170 系统的效益值最优值也更高。 [参考文献] (References) 175 180 185 190 [1] MITOLA J, MAGUIRE G Q. Cognitive radio: Making software radios more personal[J]. IEEE Personal Communications, 1999, 6(4): 13-18. [2] 张北伟，朱云龙，胡琨元.基于粒子群算法的认知无线电频谱分配算法[J].计算机应用，2011,31（12） [3] Chantaraskul S, Moessner K. Implementation of a genetic algorithm-based decision making framework for opportunistic radio[J].Communications, IET,2010,4(5):495- 506 [4] 崔珊珊.遗传算法的一些改进及其应用[D].合肥:中国科学技术大学,2010. [5] POVALAC K, MARSALEK R.Adjusting of the multicarrier communication system using binary particle swarm optimization[ C]. IEEE International Conference on Radio elektronika,2009:251-254 [6] PENG C Y,ZHENG H T,ZHAO B Y.Utilization and fairness in spectrum assignment for opportunistic spectrum access[J].Mobile Netw Appl (2006) 11:555-576 [7] 赵知劲,彭 振,郑仕链.基于量子遗传算法的认知无线电频谱分配[J].物理学报,2009,58(2):1358-1363 [8] EBERHEART R, KENNEDY J. A new optimizer using particle swarm theory[C] Proccedings of the 6th IEEE International Symposium on Micro Machine and Human Science. Piscataway:IEEE,1995:39-43 [9] KENNEDY J, EBERHART R.Particle swarm optimization[C].Proceedings of IEEE International Conference on Neural Networks.Perth:IEEE,1995:1942-1948 [10] KENNEDY J, EBERHART R. A discrete binary version of the particle swarm algorithm[C].Proceedings of IEEE International Conference on Computational Cybernetics and Simulation.Orlando:IEEE,1997:4104-4108. [11] Richards M, Ventura D. Choosing a starting configuration for particle swarm optimization.Proc.IEEE Int. Joint. Conf.Neural Netw,2004:2309-2312 - 6 - 0102030405060708090100220240260280300320340360380适应度曲线迭代次数系统总效益值 CBPSOBPSOSGA
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料