2003年吉林四平中考数学真题及答案.doc-资料库

第1页 / 共7页

第2页 / 共7页

第3页 / 共7页

第4页 / 共7页

第5页 / 共7页

第6页 / 共7页

第7页 / 共7页

2003 年吉林四平中考数学真题及答案一、填空题（每题 2 分，共 20 分） 1. 2 的相反数是 3 ； 2. 函数 y  x 2 的自变量 x 的取值范围是； 3. 不等式组 0 x  2 01 x     的解集是； 4. 已知一元二次方程 2 x 5  x  6 0 的两个根分别为 x1，x2，则 5. 点 A（1，6）在双曲线 y  上，则 k＝ k x ； 6. 如图，∠1 十∠2 十∠3 十∠4＝度． 2 x  ＝ 1 x 2 2 ； 7. 如图，四边形 ABCD 内接于⊙O，则 x＝度。 8. 某商品的标价是 1100 元，打八折（按标价的 80％）出售，仍可获利 10％，则此商品的进价是元． 9. 小明的身高是 1．6 米，他的影长是 2 米．同一时刻古塔的影长是 18 米，则古塔的高是米． 10. 如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为 7cm ，则正方形 A 、 B 、 C 、 D 的面积的和是 2cm ．二、选择题（每题 3 分，共 18 分）把下列各题中惟一正确答案的序号填在题后的括号内． 11. 下列计算正确的是（）．（A）a· 3a ＝ 3a （C）  32a ＝ 5a （B） 2a · 3a ＝ 6a （D） 5a ＋ 5a ＝2 5a 12. 今年 6 月 1 日，举世瞩目的三峡工程正式下闸蓄水，26 台机组年发电量将达到 84 700 000

000 千瓦时，用科学记数法应表示为（）．（A）8．47× 1010 千瓦时（B）8．47 × 810 千瓦时（C）8．47× 910 千瓦时（D）8．47 × 1110 千瓦时 13. 某超市一月份的营业额为 200 万元，三月份的营业额为 288 万元．如果每月比上月增长的百分数相同，则平均每月的增长率是（（A）10％（B）15％（C）20％）。（D） 25％ 14. 关于 x 的一元二次方程 2 x   m 2   mx  2 2  0 有两个不相等的实数根，则 m 的取值范围是（（A）m>1 ）．（B）m<1 （C）m＞l （D）m＜－l 15. 如图，菱形花坛 ABCD 的边长为 6 m，∠B＝60°，其中由两个正六边形组成的图形部分种花，则种花部分的图形的周长（粗线部分）为（）．（A） 3 12 m （B）20m （C）22m （D）24m 16. 如图,⊙O 的弦 AB 垂直于直径 MN 为垂足．若 OA＝5cm，下面四个结论中可能成立的是）．（（A）AB＝12cm （B）OC＝6cm （C）MN＝8cm （D）AC＝2．5cm 三、（每题 5 分，共 20 分） 17. 下面四个图形中，从几何图形的性质考虑，哪一个与其它三个不同？请指出这个图形，并简述你的理由．答：图形；理由是： 18. 化简并求值： 2 a  2 a 2 a  1  1  1  1 a （其中，a＝ 12  ）；

19. 圆心角都是 90°的扇形 OAB 与扇形 OCD 如图所示那样叠放在一起，连结 AC、BD． ⑴ 求证：△AOC≌△BOD； ⑵ 若 OA＝3cm，OC＝1cm，求阴影部分的面积． 20. 如图，①是某城市三月份 1 至 10 日的最低气温随时间变化的图象． ⑴ 根据图①提供的信息，在图②中补全直方图； ⑵ 这 10 天最低气温的众数是低气温的平均数是 ℃． ℃，最低气温的中位数是 ℃，最四、（每题 6 分，共 18 分） 21. 工人师傅做铝合金窗框分下面三个步骤进行： ⑴ 先截出两对符合规格的铝合金窗料（如图①），使 AB＝CD，EF＝GH； ⑵ 摆放成如图②的四边形，则这时窗框的形状是形，根据的数学道理是： ⑶ 将直角尺靠紧窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④），说明窗框合格，这时窗框是形，根据的数学道理是：；； 22. 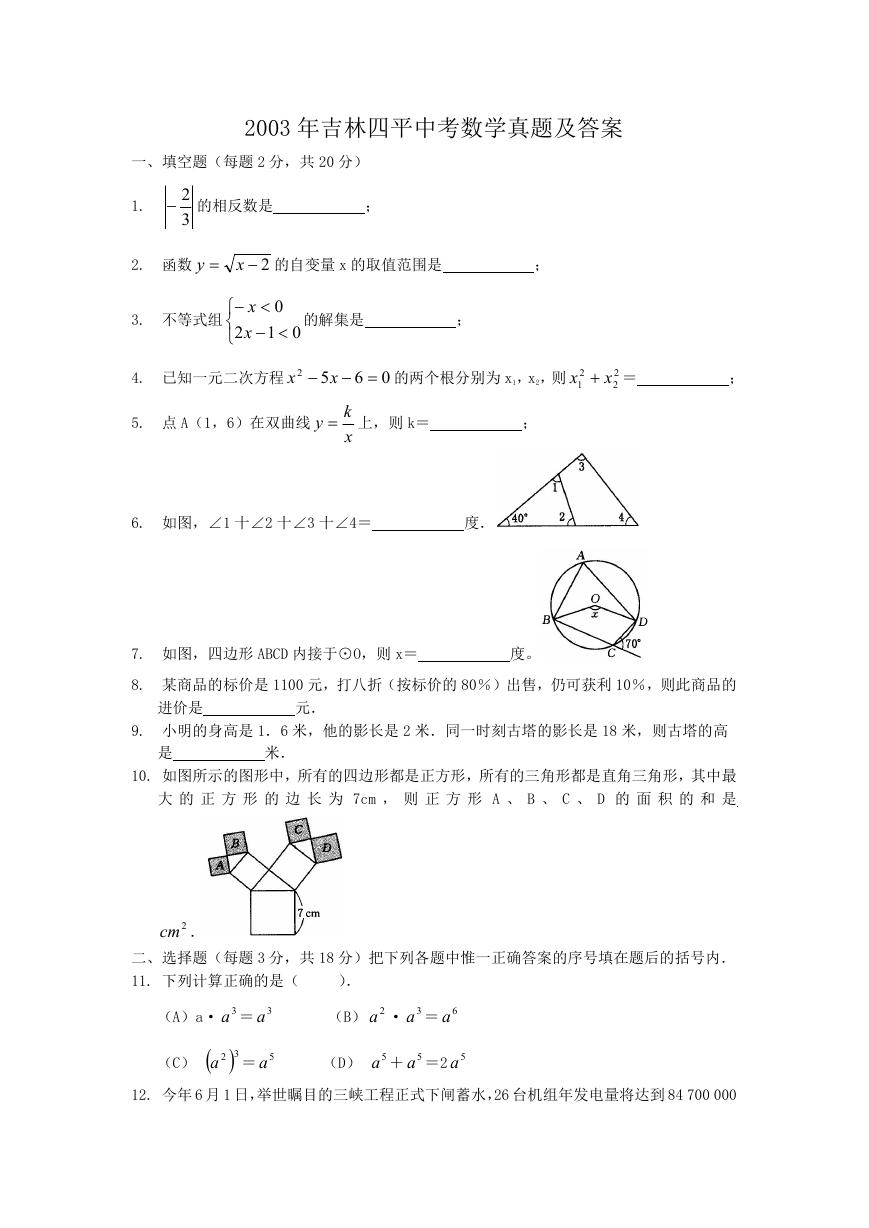如图，山脚下有一棵树 AB，小强从点 B 沿山坡向上走 50 米到达点 D，用高为 1.5 米的测角仪 CD 测得树顶的仰角为 10°．已知山坡的坡角为 15°，求树 AB 的高（精确到 0．l 米，已知 sin10°≈0．17，cos10°≈0．98，tan10°≈0．18，sin15°≈ 0．26，cos15° ≈0．97，tan15°≈0．27）． 23. 如图，小明家、王老师家、学校在同一条路上．小明家到王老师家的路程为 3 千米，王老师家到学校的路程为 0．5 千米．由于小明的父母战斗在抗“非典”第一线，为了使他能按时到校，王老师每天骑自行车接小明上学．已知王老师骑自行车的速度是步行速度的 3 倍，每天比平时步行上班多用了 20 分钟．问王老师的步行速度及骑自行车的速

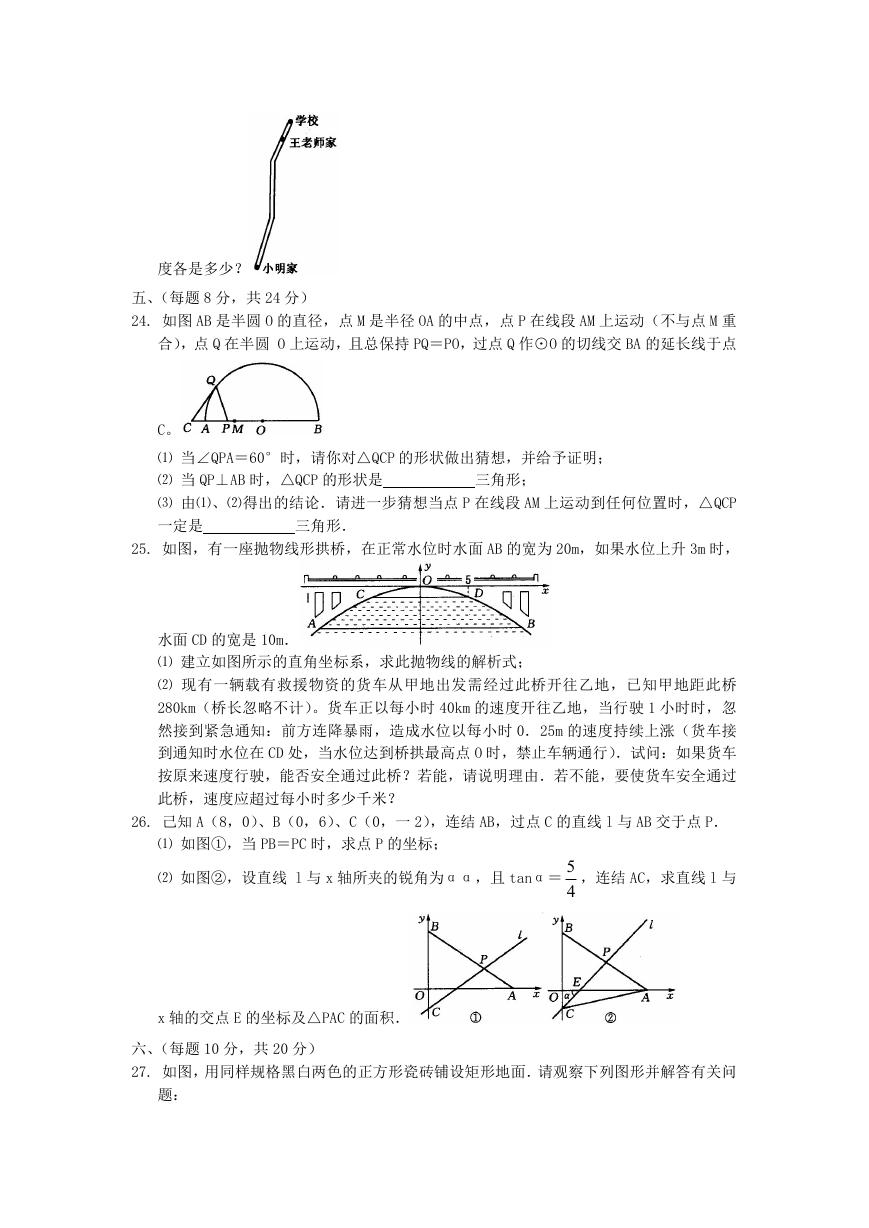
度各是多少？五、（每题 8 分，共 24 分） 24. 如图 AB 是半圆 O 的直径，点 M 是半径 OA 的中点，点 P 在线段 AM 上运动（不与点 M 重合），点 Q 在半圆 O 上运动，且总保持 PQ＝PO，过点 Q 作⊙O 的切线交 BA 的延长线于点 C。 ⑴ 当∠QPA＝60°时，请你对△QCP 的形状做出猜想，并给予证明； ⑵ 当 QP⊥AB 时，△QCP 的形状是 ⑶ 由⑴、⑵得出的结论．请进一步猜想当点 P 在线段 AM 上运动到任何位置时，△QCP 一定是三角形．三角形； 25. 如图，有一座抛物线形拱桥，在正常水位时水面 AB 的宽为 20m，如果水位上升 3m 时，水面 CD 的宽是 10m． ⑴ 建立如图所示的直角坐标系，求此抛物线的解析式； ⑵ 现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥 280km（桥长忽略不计）。货车正以每小时 40km 的速度开往乙地，当行驶 1 小时时，忽然接到紧急通知：前方连降暴雨，造成水位以每小时 0．25m 的速度持续上涨（货车接到通知时水位在 CD 处，当水位达到桥拱最高点 O 时，禁止车辆通行）．试问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由．若不能，要使货车安全通过此桥，速度应超过每小时多少千米？ 26. 己知 A（8，0）、B（0，6）、C（0，一 2），连结 AB，过点 C 的直线 l 与 AB 交于点 P． ⑴ 如图①，当 PB＝PC 时，求点 P 的坐标； ⑵ 如图②，设直线 l 与 x 轴所夹的锐角为αα，且 tanα＝ 5 4 ，连结 AC，求直线 l 与 x 轴的交点 E 的坐标及△PAC 的面积．六、（每题 10 分，共 20 分） 27. 如图，用同样规格黑白两色的正方形瓷砖铺设矩形地面．请观察下列图形并解答有关问题：

块瓷砖，每一坚列共有 ⑴ 在第 n 个图中，每一横行共有瓷砖（均用含 n 的代数式表示）； ⑵ 设铺设地面所用瓷砖的总块数为 y，请写出 y 与（1）中的 n 的函数关系式（不要求写自变量 n 的取值范围）； ⑶ 按上述铺设方案，铺一块这样的矩形地面共用了 506 块瓷砖，求此时 n 的值； ⑷ 若黑瓷砖每块 4 元，白瓷砖每块 3 元，在问题⑶中，共需花多少元钱购买瓷砖？ ⑸ 是否存在黑瓷砖与白瓷砖块数相等的情形？请通过计算说明为什么？块 28. 如图①，在矩形 ABCD 中，AB＝10cm，BC＝8cm．点 P 从 A 出发，沿 A、B、C、D 路线运动，到 D 停止；点 Q 从 D 出发，沿 D→C→B→A 路线运动，到 A 停止．若点 P、点 Q 同时出发，点 P 的速度为每秒 1cm，点 Q 的速度为每秒 2cm，a 秒时点 P、点 Q 同时改变速度，点 P 的速度变为每秒 bcm，点 Q 的速度变为每秒 dcm．图②是点 P 出发 x 秒后上△ APD 的面积 S1（ 2cm ）与 x（秒）的函数关系图象；图③是点 Q 出发 x 秒后△AQD 的面积 S2（ 2cm ）与 x（秒）的函数关系图象． ⑴ 参照图②，求 a、b 及图②中 c 的值； ⑵ 求 d 的值； ⑶ 设点 P 离开点 A 的路程为 y1（cm），点 Q 到点 A 还需走的路程为 y2（cm），请分别写出动点 P、Q 改变速度后 y1、y2 与出发后的运动时间 x（秒）的函数关系式，并求出 P、 Q 相遇时 x 的值． ⑷ 当点 Q 出发秒时，点 P、点 Q 在运动路线上相距的路程为 25cm．

资料库

2003年吉林四平中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料