数据预处理-特征选择.pdf

发布时间：2022-06-19 发布人：admin 分类：说明书资料大小：1.00M 资料格式：pdf 举报版权申诉

a21d4b18-9a2d-45ce-9c08-56429efd6465.pdf-第1页.png

第1页 / 共15页

a21d4b18-9a2d-45ce-9c08-56429efd6465.pdf-第2页.png

第2页 / 共15页

a21d4b18-9a2d-45ce-9c08-56429efd6465.pdf-第3页.png

第3页 / 共15页

a21d4b18-9a2d-45ce-9c08-56429efd6465.pdf-第4页.png

第4页 / 共15页

a21d4b18-9a2d-45ce-9c08-56429efd6465.pdf-第5页.png

第5页 / 共15页

a21d4b18-9a2d-45ce-9c08-56429efd6465.pdf-第6页.png

第6页 / 共15页

a21d4b18-9a2d-45ce-9c08-56429efd6465.pdf-第7页.png

第7页 / 共15页

a21d4b18-9a2d-45ce-9c08-56429efd6465.pdf-第8页.png

第8页 / 共15页

单特征的AUC和多特征的AUC的AUC理解总结

特征离散化、特征交叉总结

特征交叉

特征离散化

相关的残差分析总结

特征选择方法

方差选择法

卡方检验

互信息特征选择

逻辑回归计算特征重要度

皮尔逊相关系数

距离相关系数

箱线图

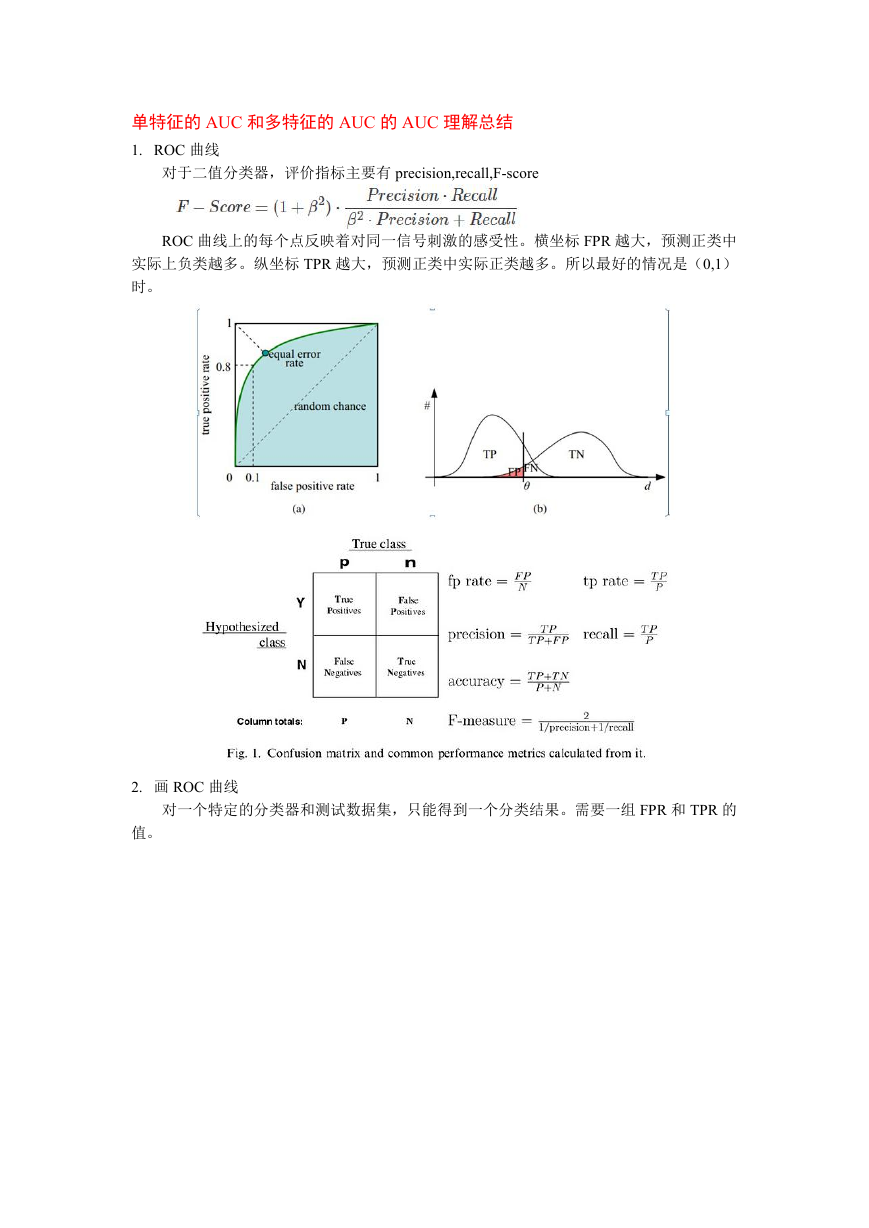
单特征的 AUC 和多特征的 AUC 的 AUC 理解总结 1. ROC 曲线对于二值分类器，评价指标主要有 precision,recall,F-score ROC 曲线上的每个点反映着对同一信号刺激的感受性。横坐标 FPR 越大，预测正类中实际上负类越多。纵坐标 TPR 越大，预测正类中实际正类越多。所以最好的情况是（0,1）时。 2. 画 ROC 曲线对一个特定的分类器和测试数据集，只能得到一个分类结果。需要一组 FPR 和 TPR 的值。

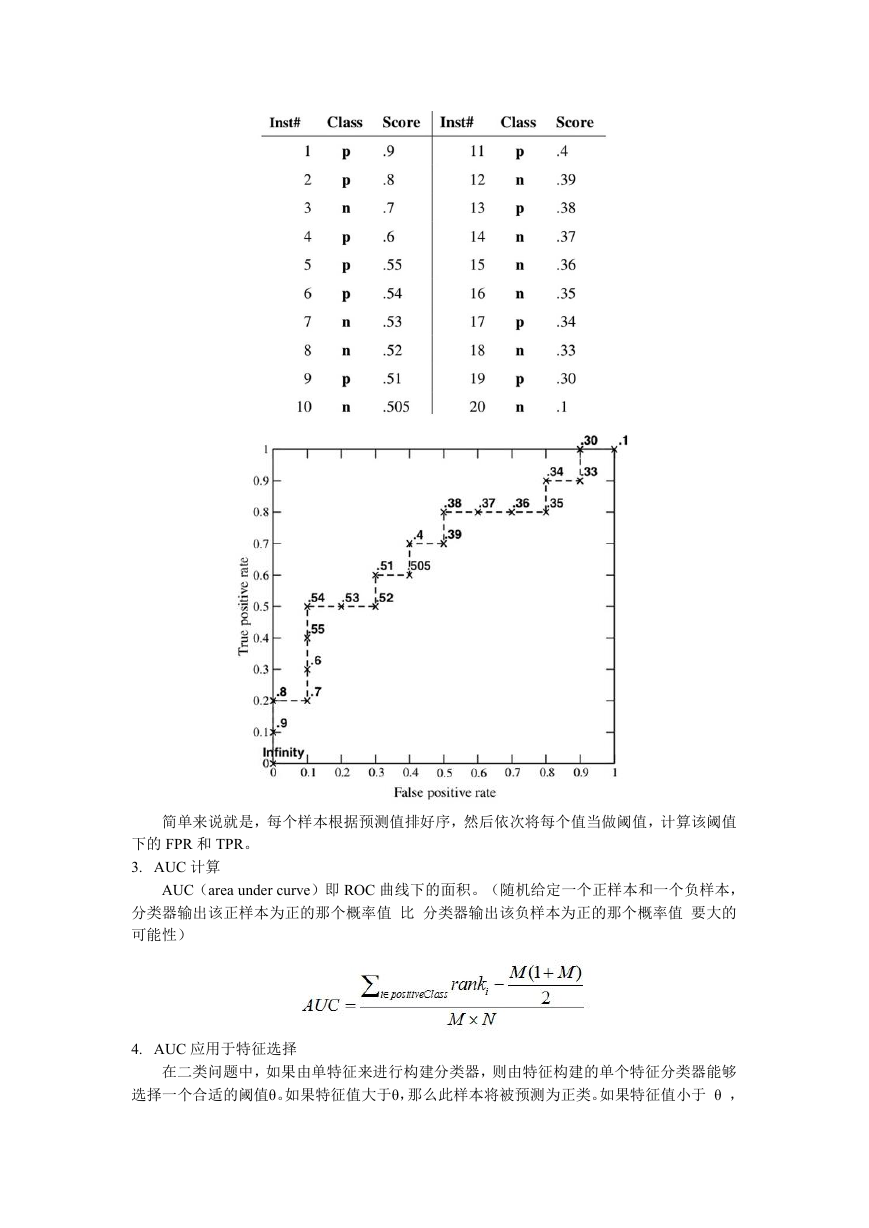
简单来说就是，每个样本根据预测值排好序，然后依次将每个值当做阈值，计算该阈值下的 FPR 和 TPR。 3. AUC 计算 AUC（area under curve）即 ROC 曲线下的面积。（随机给定一个正样本和一个负样本，分类器输出该正样本为正的那个概率值比分类器输出该负样本为正的那个概率值要大的可能性） 4. AUC 应用于特征选择在二类问题中，如果由单特征来进行构建分类器，则由特征构建的单个特征分类器能够选择一个合适的阈值θ。如果特征值大于θ，那么此样本将被预测为正类。如果特征值小于 θ ，

那么此样本将被预测为负类。特征的分类预测能力，正是特征与类别之间的相关性的一种体现，即一个特征与目标类别之间的相关性越大，这个特征的分类预测能力越强。随着阈值θ 的改变，能够得到不同的分类结果，同时也可得到相应的 FPR 和 TPR。刻画 ROC 曲线，并计算 AUC 值，则 AUC 值越大，特征对分类结果带来的影响亦越强。若我们对一个具有较多特征的数据集进行分类时，而数据集的特征又明显较多，此时，并不好对每个特征进行 AUC 计算。不妨，将特征集合划分为多个特征子集，针对每个特征子集进行模型训练，即可根据模型的预测结果得到训练集/测试集上的 AUC 值，并以此 AUC 值作为标准，选择具有最大 AUC 值的特征子集作为特征选择方案。参考链接 https://tracholar.github.io/machine-learning/2018/01/26/auc.html https://www.cnblogs.com/sddai/p/8360089.html https://blog.csdn.net/misscrush/article/details/80090097 孙蕾. 基于 AUC 和特征间互补性的特征选择方法[D].南开大学,2017. 特征离散化、特征交叉总结特征交叉 1. 什么是特征交叉特征交叉一种合成特征的方法，可以在多维特征数据集上，进行很好的非线性特征拟合。假设一个数据集有特征 x1 和 x2，那么引入交叉特征值 x3，使得：那么最终的表达式为： 2. 为什么进行特征交叉很多情况下，数据的预测值和各个特征值之间不是线性的关系，比如下图：无法找到一个直线把蓝色和黄色的点分离开，此时就等使用特征交叉的方式，进行拟合。当然，也可以使用神经网络。特征交叉是一种让线性模型学习到非线性模型的方式。 3. 特征交叉的方式使用 One-Hot 向量的方式进行特征交叉。这种方式一般适用于离散的情况，很少用于连续的数据集上。我们可以把特征交叉看成数据的逻辑与操作。

比如给出分档的经纬度数据：经过交叉后，得到新的数据集，特征交叉本质上是一个笛卡尔积，两个特征列进行笛卡尔积。笛卡尔积中，如果同时满足两者的条件，则结果为 1；否则为 0，因此这种方式更加适合离散型的数据特征。一般来说，先把数据进行分档处理，再把分档的结果进行特征交叉，此时可以获得更好的数据特征，分档处理可以对数据降维，从而极大地简化计算量。 4. 数据分档下图表示了数据集中，纬度对房价的影响。主要数据集中在 34 度和 38 度附近。单独使用浮点型数据，对房价的预测不恰当。因为纬度和房价之间不是线性关系。为了更好的描述二者之间的关系，进行数据分档操作：

因此，这个数据集形成了一个 11 维的向量，如果表示 37.4 度，可以使用 [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0] 5. 特征交叉的典型应用比如在地图的方面的处理中，需要用到特征交叉。下图的房价和经纬度中，单纯的给出经度或者纬度，都不能直接反应房价和地理位置的关系。更好的方式为经度和纬度交叉点，才能表示位置。图片中，先对数据进行分档处理，也就是经度和纬度分别分割成 100 的数据段，然后把分段后的数据列进行特征交叉，那么每个房屋会对应一个 1000 维的特征向量，二维的位置信息会转化成一维的位置向量，只有精确的位置点的数据才是 1，其余的都是 0 参考链接 https://blog.csdn.net/qq_35976351/article/details/80892902 https://blog.csdn.net/qq_35976351/article/details/80876628 特征离散化 1. 特征离散化的意义数据通常以混合的形式出现：nominal,discrete,continuous。离散或者连续型数据属于定序数据类型（ordinal data types）,数据之间有次序，而对于定类数据类型（nominal data types）, 数据之间并无次序。对于连续型属性其取值个数是无限大的，离散属性取值通常是有限的。相比于连续特征，离散特征具有以下优点：（1）离散特征的增加和减少都很容易，易于模型的快速迭代；（2）稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；（3）离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30 是 1，否则 0。如果特征没有离散化，一个异常数据“年龄 300 岁”会给模型造成很大的干扰；（4）逻辑回归中，它属于广义线性模型，表达能力受限。单变量离散化为 N 个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；（5）离散化后可以进行特征交叉，假如特征 A 离散化为 M 个值，特征 B 离散为 N 个值，那么交叉之后会有 M*N 个变量，进一步引入非线性，提升表达能力；（6）特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30 作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；按区间离散化，划分区间是非常关键的。

（7）特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。(当使用连续特征时，一个特征对应于一个权重，那么，如果这个特征权重较大，模型就会很依赖于这个特征，这个特征的一个微小变化可能会导致最终结果产生很大的变化，这样子的模型很危险，当遇到新样本的时候很可能因为对这个特征过分敏感而得到错误的分类结果，也就是泛化能力差，容易过拟合。而使用离散特征的时候，一个特征变成了多个，权重也变为多个，那么之前连续特征对模型的影响力就被分散弱化了，从而降低了过拟合的风险。) 模型是使用离散特征还是连续特征，其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型，也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。通常来说，前者容易，而且可以 n 个人一起并行做，有成功经验；后者目前看很赞，能走多远还须拭目以待。 2. 离散化处理的一般过程  对连续特征值按照某种指定的规则进行排序  初步确定连续属性的划分断点  按照某种给定的判断标准继续分割断点或合并断点  如果第三步得到判断标准的终止条件，则终止整个连续特征离散化的过程，否则继续按第三步执行 3. 离散化方法的分类主要的分类体系有无监督的和有监督的（又分为建立在错误码率、熵值或者统计信息基础上的离散化方法，典型代表是等频、等宽的连续特征离散化方法）、动态的和静态的、全局的和局部的、分列式的（从上至下）和合并式的（从下至上）、单变量的和多变量的以及直接的和增量式的。（1）无监督的方法无监督方法都具有的问题就是都需要事先规定划分区间这个参数，常用的方法有分箱法和直观划分，首先来说一下分箱法：分箱法又分为等宽分箱法和等频分箱法，其实从名字就能看出算法的做法了，前者制定定长的间隔将特征放入不同箱子内，后者根据频率划分箱子，这两种做法都有一定的缺陷。  等宽分箱法对异常点比较敏感，比如数据正常范围是 30-60，现在出现了一个特征本来是 30 不小心读取成了 300，那么宽度会被拉长，实例就主要集中在前面的箱体中，后

面的箱体几乎没有实例，解决的方法主要是设立阈值移除阈值以外的实例。  等频分箱法的缺陷是完全按照频率划分会出现实例特征相同却不在同一个箱体内的情况，解决办法也很简单，在划分完成后进行微调就可完成。  基于 K-Means 的聚类分箱方法（2）有监督的方法 1R 方法 1R 是一种使用分箱的有监督的方法。它把连续的区间分成小的区间，然后再使用类标签对小区间的边界进行调整。每个区间至少包含 6 个实例，除了最后一个区间外，最后一个区间包含所有未被列入其他区间的实例。从第一个实例开始，把前 6 个实例列入第一区间，如果下一个实例与此区间中大多数实例的类标签相同，则把此实例加入区间中，再判定下一个实例按照前述操作能否加入刚才的区间中，否则形成下一个含 6 个实例的新的区间，对下一个实例重复类似的操作，直至结束。然后把区间中的大多数实例的共同类标签作为此区间的类标签，如果相邻区间经过此操作后有相同的类标签，则应把这两个相邻区间合并。 1R 离散化方法也是分箱方法，操作仍然比较方便，但又不再需要用户人为指定箱的个数，也克服了无监督的分箱方法的不使用类信息的缺陷，并且能避免把具有相同特征值相同类标签的实例分入不同的小区间中。卡方检验（CHI）找到一个分裂点看，左右 2 个区间，在目标值上分布是否有显著差异，有显著差异就分裂，否则就忽略。这个点可以每次找差异最大的点。合并类似，先划分如果很小单元区间，按顺序合并在目标值上分布不显著的相邻区间，直到收敛。卡方值通常由χ2 分布近似求得。 χ2 表示观察值与理论值之问的偏离程度。计算这种偏离程度的基本思路如下: 设 A 代表某个类别的观察频数，E 代表基于 H0 计算出的期望频数，A 与 E 之差称为残差。显然，残差可以表示某一个类别观察值和理论值的偏离程度，但如果将残差简单相加以表示各类别观察频数与期望频数的差别，则有一定的不足之处。因为残差有正有负，相加后会彼此抵消，总和仍然为 0，为此可以将残差平方后求和。另一方面，残差大小是一个相对的概念，相对于期望频数为 10 时，期望频数为 20 的残差非常大，但相对于期望频数为 1 000 时 20 的残差就很小了。考虑到这一点，人们又将残差平方除以期望频数再求和，以估计观察频数与期望频数的差别。进行上述操作之后，就得到了常用的χ2 统计量，由于它最初是由英国统计学家 Karl Pearson 在 1900 年首次提出的，因此也称之为 Pearson χ2，其计算公式为当 n 比较大时，χ2 统计量近似服从 k-1(计算 Ei 时用到的参数个数)个自由度的卡方分布。信息增益法（IG）这个和决策树的学习很类似。分裂方法，就是找到一个分裂点看，左右 2 个区间，看分裂前后信息增益变化阈值，如果差值超过阈值（正值，分列前-分裂后信息熵），则分裂。每次找差值最大的点做分裂点，直到收敛。合并类似，先划分如果很小单元区间，按顺序合并信息增益小于阈值的相邻区间，直到收敛。 4. 离散化方法的评价  区间的个数：是对模型简洁性的要求  离散化所导致的不一致性：离散化后的不一致性不能比离散化之前高。

 预测准确性：通常通过交叉检验模式建立分叉树来衡量。  具有最简单的离散化结果参考链接 http://www.360doc.com/content/17/0708/10/1489589_669774278.shtml https://blog.csdn.net/u012022003/article/details/79628725 https://blog.csdn.net/weixin_42933718/article/details/88952165 相关的残差分析总结 1. 残差分析定义在回归模型中，假定的期望值为 0，方差相等且服从正态分布的一个随机变量。但是，若关于的假定不成立，此时所做的检验以及估计和预测也许站不住脚。确定有关的假定是否成立的方法之一是进行残差分析（residual analysis）. 2. 残差与残差图残差（residual）是因变量的观测值与根据估计的回归方程求出的预测之差，用 e 表示。反映了用估计的回归方程去预测而引起的误差。第 i 个观察值的残差为：常用残差图：有关 x 残差图，有关的残差图，标准化残差图有关 x 残差图：用横轴表示自变量 x 的值，纵轴表示对应残差，每个 x 的值与对应的残差用图上的一个点来表示。分析残差图，首先考察残差图的形态及其反映的信息。分析：（a）对所有 x 值，的方差都相同，且描述变量 x 和 y 之间的回归模型是合理的，残差图中的所有点落在一条水平带中间。（b）对所有的值，的方差是不同的，对于较大的 x 值，相应的残差也较大，违背了的方差相等的假设（c）表明所选的回归模型不合理，应考虑曲线回归或多元回归模型 3. 标准化残差对于正态性假定的检验，也可通过标准化残差分析完成。标准化残差（standardized residual）是残差除以其标准差后得到的数值，也称 Pearson 残差或半学生化残差（semi-studentized residuals）,用表示。第 i 个观察值的标准化残差为：

分享到：

赞收藏

资料库

数据预处理-特征选择.pdf

相关推荐

人工智能

热门标签

最新资料