基于最大相关熵的多凸组合滤波器.pdf-资料库

weixin_38639642-12931353-16359647601141216572.pdf-第1页.png

第1页 / 共6页

weixin_38639642-12931353-16359647601141216572.pdf-第2页.png

第2页 / 共6页

weixin_38639642-12931353-16359647601141216572.pdf-第3页.png

第3页 / 共6页

weixin_38639642-12931353-16359647601141216572.pdf-第4页.png

第4页 / 共6页

weixin_38639642-12931353-16359647601141216572.pdf-第5页.png

第5页 / 共6页

weixin_38639642-12931353-16359647601141216572.pdf-第6页.png

第6页 / 共6页

基于最大相关熵的多凸组合滤波器基于最大相关熵的多凸组合滤波器相关熵被广泛地应用于非高斯信号处理中，但是也不可避免步长与失调量之间的矛盾。为了解决这个矛盾，基于最大相关熵的凸组合(Convex combination of Maximum Correntropy Criterion，CMCC)滤波器被提出，以同时获得大步长滤波器的快收敛速度和小步长滤波器的低失调量。但是，当两个步长不同的滤波器进行凸组合时，由于步长选取的差异，会导致组合滤波器的收敛速度和追踪最优值的能力下降。因此，提出了基于最大相关熵的多凸组合滤波器（Multi-convex Combination of Maximum Correntropy Criterion, MCMCC）。MCMCC 算法能够提供数量更多不同步长的自适应滤波器，使得组合滤波器可以灵活地调节多个步长的权重占比，从而具有更好的追踪能力。仿真结果表明，在针对混合高斯噪声和突变的系统辨识中，MCMCC算法相比CMCC算法具有更快的收敛速度、再收敛能力和追踪能力。 0 引言引言自适应滤波技术被广泛地应用在信号处理和机器学习的许多不同的领域，如信道估计、噪声消除和系统辨识等。滤波器算法设计是更新滤波器的参数使其尽可能更接近理想响应[1]。自适应滤波器的优化准则和代价函数是滤波器设计的核心。常见的优化准则或代价函数分别是最小均方差(Minimum Mean Square Error，MMSE)准则、最小误差熵(Minimum Error Entropy，MEE)代价函数和最大相关熵准则(Maximum Correntropy Criterion，MCC)[2]。MMSE准则的代表算法为最小均方算法(Least Mean Square，LMS)。LMS算法因为其较低的复杂度和计算量，所以常适用于线性和高斯噪声的情况。MEE代价函数在非高斯噪声和非线性结构中表现出了很强的鲁棒性，并且具有表征数据整个结构的能力。但是，它的计算复杂度相当大。 MCC代价函数由于权重更新中指数部分的存在，使得在脉冲干扰和非线性系统中表现出很强的鲁棒性，并且有着与LMS相近的复杂度和与MEE相近的性能。因此，本文采取的自适应准则为MCC。 MCC是采用核心宽度来决定局部量，它对出界量和脉冲噪声造成的有害影响有很好的抑制效果。在文献[3]中，研究者已经介绍最大相关熵的本质就是一种平滑的后验估计。在文献[2]、[4]中，介绍了MCC被引入到自适应滤波器中在非高斯噪声下可以有效地提高追踪能力。同时，在文献[5]也对MCC的稳态均方差性能进行了详细的推导。众所周知，自适应滤波器中最重要的矛盾就是收敛速度与失衡量之间的矛盾，即收敛速度与失衡量成反比。这种矛盾在基于MCC的自适应滤波器中也不例外。在基于最大相关熵的自适应滤波器中，收敛速度由步长与kernel宽度决定。当kernel宽度一定时，滤波器的步长越大收敛速度越快，但失调量也越高；步长越小失调量越低，但收敛速度越慢。为了解决这个问题，文献[6]将最近比较流行的凸组合方式引入到最大相关熵自适应滤波器中，使得组合滤波器不仅得到了大步长的滤波器快收敛速度，还得到了小步长的滤波器的低失调量。但是在CMCC滤波器中，由于两个滤波器的步长选取的问题，从而导致组合滤波器的收敛和追踪性能下降。基于上述讨论，本文提出了基于最大相关熵的多凸组合滤波器。在MCMCC滤波器中，每个基于MCC的自适应滤波器都表现出很好的追踪性能，所以MCMCC可以有效地追踪各种各样的改变。 1 基于最大相关熵的凸组合自适应滤波器基于最大相关熵的凸组合自适应滤波器根据自适应算法的随机梯度原则，基于最大相关熵的权重系数更新方程为[7]：其中，y1(k)=XTW1(k)和y2(k)=XTW2(k)分别表示大步长滤波器和小步长滤波器的输出。大步长滤波器和小步长滤波器的权重分

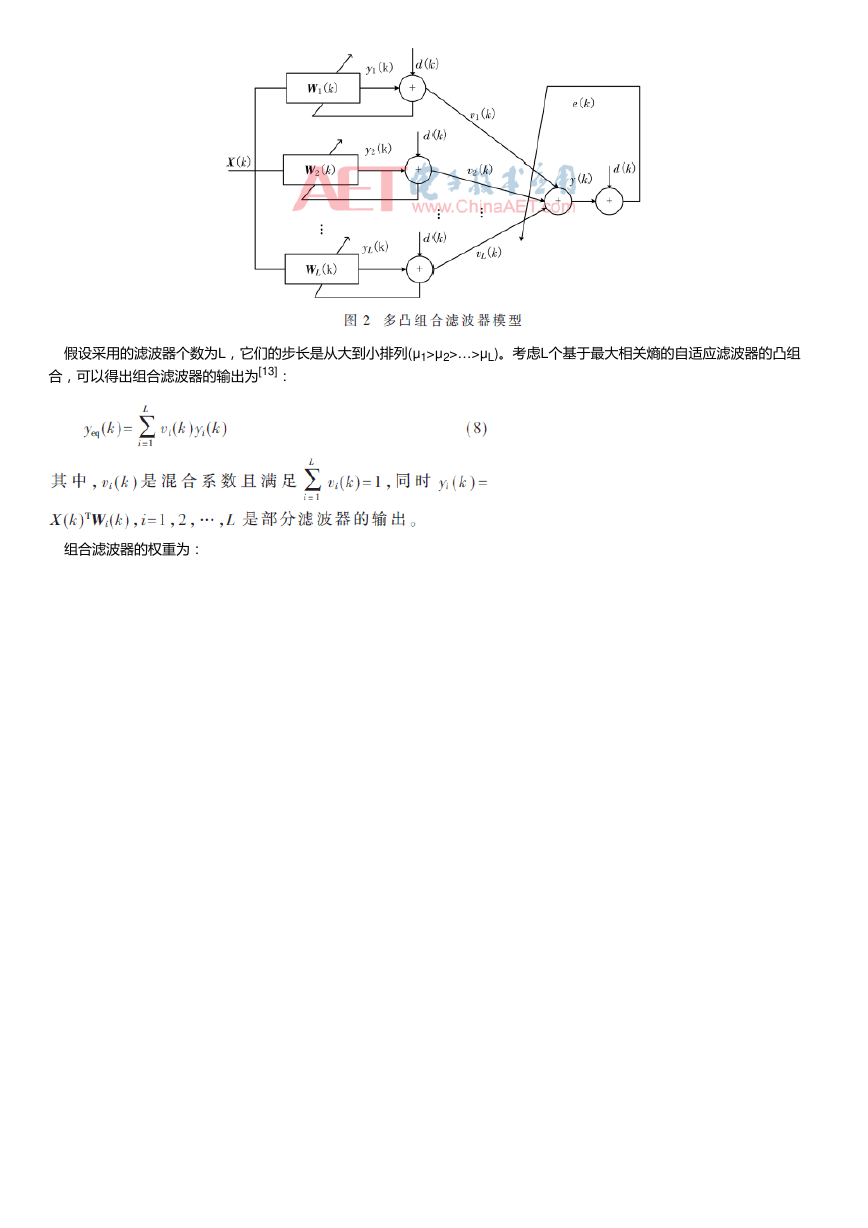
别表示为：其中，e(k)=d(k)-y(k)表示组合误差；μα表示参数α(k)在基于最大相关熵准则下的步长，并且μα必须设定为远大于λ1，以保证组合滤波器的自适应速度快于大步长的滤波器的自适应速度；α(k)的取值范围限定在[-4，4]，以防止v(k)和1-v(k)接近0而导致算法停止[12]。同时，基于MCC的凸组合滤波器的性能还可以继续被优化，通过引入权重转移的方法。该方法是用步长大的滤波器的权重去加速步长小的滤波器的权重[6]。 2 多凸组合的最大相关熵的自适应滤波器多凸组合的最大相关熵的自适应滤波器由以上的分析可知，凸组合自适应滤波器是凸组合两个步长不同的滤波器。多凸组合滤波器就是把多个步长不同的滤波器进行凸组合。本文所提到的基于最大相关熵的多凸组合自适应滤波器就是多个步长不同的基于最大相关熵准则的滤波器进行凸组合。多凸组合的滤波器模型如图2所示。接下来介绍基于最大相关熵的多凸组合滤波器的各个参数的设定。

假设采用的滤波器个数为L，它们的步长是从大到小排列(μ1>μ2>…>μL)。考虑L个基于最大相关熵的自适应滤波器的凸组合，可以得出组合滤波器的输出为[13]：组合滤波器的权重为：

类似于CMCC滤波器，基于MCC的多凸组合滤波器的性能也可以继续被优化，通过引入改进后的权重转移的方法。该方法是用组合的滤波器的权重去加速其他所有比组合滤波器收敛速度慢的滤波器的权重。第i个滤波器改进后的权重为：其中，β是转移系数。使用式(13)的条件是组合滤波器明显优于部分滤波器。判断组合滤波器明显优于部分滤波器的方法是计算每个滤波器的相关熵的估计量。相关熵的估计量的计算为： 3 仿真结果仿真结果综上所述，可知随着凸组合滤波器个数的增加，收敛性能和追踪性能也会越来越好。但是在滤波器个数增加的同时，计算量也会线性地增长，所以为了更好地表现MCMCC的性能同时又不会造成计算量的急剧增加，本文的仿真结果采用的是4个滤

波器进行凸组合。为了进一步验证MCMCC算法的收敛性能与跟踪性能,现将MCMCC算法与CMCC算法用于系统辨识过程中进行计算机仿真分析,并分别对两种算法进行1 000次独立仿真实验,求取统计平均值。同时,为能够客观比较系统失调等性能参数,两种算法的参数均选为经过大量实验后的相对最优参数。其中CMCC算法的相关参数选择如下：取μ1=0.1，μ4=0.002；对于本文提出的 MCMCC算法,与原算法重合部分的参数仍取原参数不变，即μ1=0.1，μ4=0.002，同时选择其他两个滤波器的步长为： μ2=0.03，μ3=0.01。在本文中，性能的分析是通过归一化均方差(Normalized Mean Square Deviation，NMSD)来判定，其表示为： NMSD=10log10(||W-W0||2/||W0||2)。下面在混合高斯噪声和突变的系统辨识中比较MCMCC性能和CMCC性能。 3.1 混合高斯噪声下的性能混合高斯噪声下的性能 TX(k)+N(k)，其中假设未知系统冲激响应满足7阶FIR模型，4个MCC自适应滤波器的阶数也为7阶，理想输出为：d(k)=W0 本文设定W0=[0.9003，0.5377，-0.2137，0.028，-0.7826，-0.5242，0.0871]′；输入信号X(k)为均值0、方差1的高斯白噪声序列；噪声信号N(k)为混合高斯噪声：从图3的3幅图还可以明显地看出，在收敛过程最初始的阶段，分别是图3(a)的(0，67)、图3(b)的(0，50)、图3(c)的 (0，21)，4-MCMCC和CMCC的收敛曲线重合。这是因为在初始阶段，权重系数发生快速的变化，而4-MCMCC和CMCC都是 μ1在起作用。在收敛过程中间阶段，分别是图3(a)的(67，983)、图3(b)的(50，1021)、图3(c)的(21，1091)，4-MCMCC算法的收敛速度明显快于CMCC算法。这是因为4-MCMCC算法比CMCC算法具有更多的步长，可以更灵活地调节步长，所以可以更适应权重系数的变化，从而获得更快的收敛速度。在收敛过程进入稳态阶段时，4-MCMCC算法要比CMCC算法更快地进入稳态状态，并且4-MCMCC算法也具有低NMSD,这说明4-MCMCC算法可以用更少的迭代次数就收敛并且保持同CMCC算法一样的低NMSD，因此极大地缩小了系统渐进稳态的过渡过程。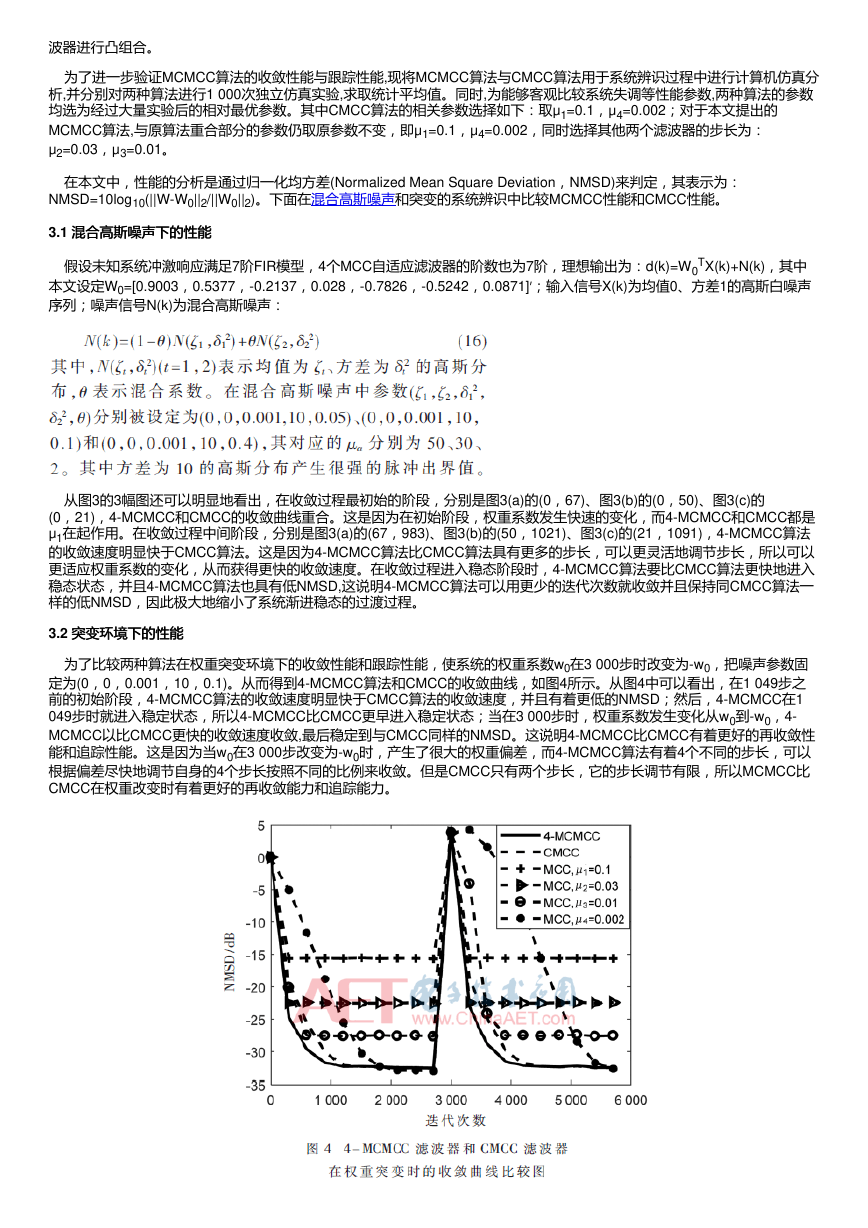 3.2 突变环境下的性能突变环境下的性能为了比较两种算法在权重突变环境下的收敛性能和跟踪性能，使系统的权重系数w0在3 000步时改变为-w0，把噪声参数固定为(0，0，0.001，10，0.1)。从而得到4-MCMCC算法和CMCC的收敛曲线，如图4所示。从图4中可以看出，在1 049步之前的初始阶段，4-MCMCC算法的收敛速度明显快于CMCC算法的收敛速度，并且有着更低的NMSD；然后，4-MCMCC在1 049步时就进入稳定状态，所以4-MCMCC比CMCC更早进入稳定状态；当在3 000步时，权重系数发生变化从w0到-w0，4- MCMCC以比CMCC更快的收敛速度收敛,最后稳定到与CMCC同样的NMSD。这说明4-MCMCC比CMCC有着更好的再收敛性能和追踪性能。这是因为当w0在3 000步改变为-w0时，产生了很大的权重偏差，而4-MCMCC算法有着4个不同的步长，可以根据偏差尽快地调节自身的4个步长按照不同的比例来收敛。但是CMCC只有两个步长，它的步长调节有限，所以MCMCC比 CMCC在权重改变时有着更好的再收敛能力和追踪能力。

4 结论结论为了克服CMCC算法中步长范围窄而导致收敛性能和追踪性能低的缺点，本文尝试将基于最大相关熵的凸组合滤波器扩展为基于最大相关熵的多凸组合滤波器。理论分析和仿真结果表明，MCMCC算法在混合高斯噪声下，相比CMCC算法，不仅提高了收敛速度，而且还保持了低的失调量。 MCMCC算法在突变权重环境下，相比CMCC算法，因为可以更灵活地调节多个步长比重，所以提高了再收敛能力和追踪能力。因此，本算法在系统识别方面具有较大的实际应用价值。参考文献参考文献 [1] WANG R，Chen Badong.A variable step-size adaptive algorithm under maximum correntropy criterion[C].IEEE International Conference on Acoustic，Speech and Signal Processing(ICASSP)，2015：1-5. [2] SINGH A，PRINCIPE J C.Using correntropy as a cost function in linear adaptive filters[C].International Joint Conference on Neural Networks，Piscataway，2009：2950-2955. [3] CHEN B，PRINCIPE J C.Maximum correntropy estimation is a smoothed MAP estimation[J].IEEE Signal Processing Letters，2012，19(8)：491-494. [4] ZHAO S，CHEN B，PRINCIPE J C.Kernel adaptive filtering with maximum correntropy criterion[C].Proceedings of International Joint Conference on Neural Networks，Piscataway，2011：2012-2017. [5] CHEN B，XING L，LIANG J，et al.Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion[J].IEEE Signal Processing Letters，2014，21(11)：880-884. [6] Shi Liming.Convex combination of adaptive filters under the maximum correntropy criterion in impulsive interference[J].IEEE Signal Process Letters，2014，21(11)：1385-1388. [7] GUIMARAES J P F，FONTES A I R，RLGO J B A，et al.Performance evaluation of the maximum correntropy criterion in identification systems[C].IEEE Conference on Evolving and Adaptive Intelligent Systems，2016：110-113. [8] LIU W，POKHAREL P，PRINCIPE J.Error entropy，correntropy and m-estimation[C].IEEE International Workshop on Machine Learning for Signal Processing，2006：179-184. [9] ARENAS-GARCIA J，FIGUEIRAS-VIDAL A R，SAYED A H.Steady state performance of convex combinations of adaptive filters[C].International Conference on Acoustics，Speech and Signal Processing，2005：33-36. [10] SHI L M，LIN Y，XIE X Z.Combination of affine projection sign algorithms for robust adaptive filtering in non-Gaussian impulsive interference[J].Electronics Letters，2014，50(6)：466-467. [11] FERRER M.Convex combination filtered-x algorithms for active noise control systems[J].IEEE Transaction on Audio Speech and Language Processing，2013，21(1)：156-167. [12] ARENAS-GARCIA J，GOMEZ-VERDEJO V，FIGUEIRAS-VIDAL A R.New algorithms for improved adaptive convex combination of LMS transversal filters[J].IEEE Transaction，2005，54(6)：2239-2249. [13] ARENAS-GARCIA J，MARTINEZ-RAMIN M，GOMEZ-VERDEJO V，et al.Multiple plant identifier via adaptive LMS convex combination[C].IEEE International Symposium on Intelligent Signal Processing，2003：137-142. 作者信息: 作者信息吴文静，梁中华，罗倩文，李巍（长安大学信息工程学院，陕西西安710064）

资料库

基于最大相关熵的多凸组合滤波器.pdf

相关推荐

开发技术

热门标签

最新资料