ITU-R 模型 ITU-R 降雨衰减预报模式，是以 Fedi 所提出的模式为基础的，其核心是采用了“等效 路径长度”的概念，即将降雨的非均匀性进行均匀化而引进能起等效作用的缩短因子，使得 缩短了的路径长度乘以单位路径衰减就正好是实际测量的降雨衰减。如今 ITU-R 第三工作会 议对地空电路降雨衰减模式进行了重大调整，既考虑了降雨沿路径的水平变化，又考虑了降 雨沿路径的垂直变化。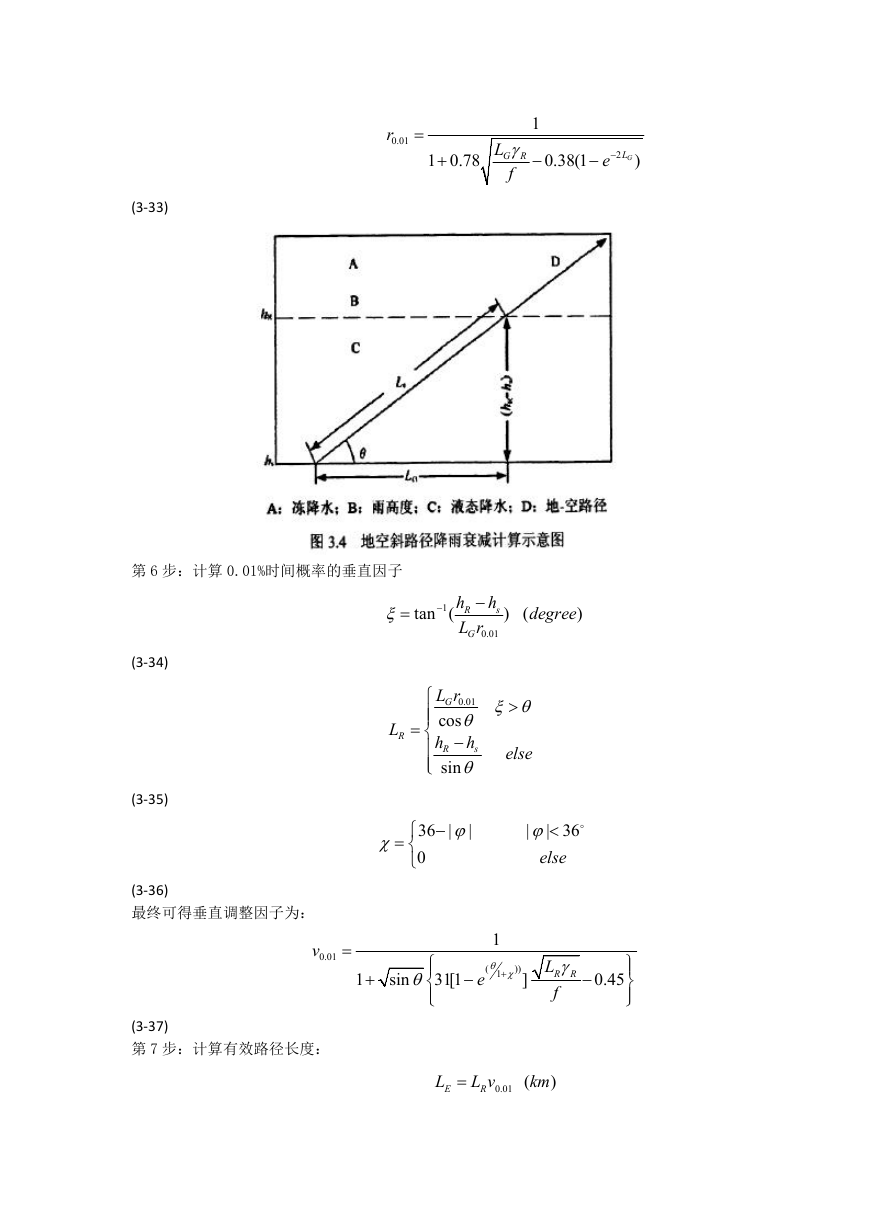ITU-R 雨衰预报模型所需要的参数归结如下： 0.01R ：当地平均年 0.01%时间概率的降雨率； sH ：地面站海拔高度 (km)； 1 ：卫星所定点的经度； ：天线仰角； f ：工作频率(GHz) 第 1 步：计算雨顶高度 Rh km ( )   5 0.075(  5  5    5 0.1(  0       23)   0 0 71  21)  2 ：地面站的经度； ：地面站纬度； eR :地球等效半径(8500km) 北半球 北半球 南半球 南半球    23   23    21    21     -71     (3-29) 第 2 步：计算雨顶下斜路径长度，如图 3.4 所示： L km s ( )  h h  s R sin  (sin 2 +         ) 2( h h  R s ) 2( h h  1/2 ) s R R e  sin    5    5  (3-30) 第 3 步：计算斜路径的水平投影： (3-31) 第 4 步：获得平均一年超过 0.01%的降雨率 0.01R ，计算 0.01%时间概率点降雨率的特征衰减： L G  L  s cos (3-32) 第 5 步：计算 0.01%时间概率的水平缩短因子   R ( k R 0.01 )  ( dB km / ) 

r 0.01  1 1 0.78  L  G R f  0.38(1  e  2 )GL (3-33) 第 6 步：计算 0.01%时间概率的垂直因子    1 tan ( h s ) ( degree ) h  R L r G 0.01 (3-34) (3-35) L R      L r 0.01 G cos  h h  s R sin     else |     36 |   0   | | 36   else (3-36) 最终可得垂直调整因子为： v 0.01  1  sin  1  1  ( ))  ]   31[1     e L  R R f  0.45      (3-37) 第 7 步：计算有效路径长度： L E  L v R 0.01 ( km ) 

(3-38) 第 8 步：计算 0.01%时间概率降雨衰减： A 0.01  L R E ( dB ) (3-39) 第 9 步：预测时间概率为 0.001%~10%的降雨衰减： 如果 P≥1，则 =0；若 P＜1，则有：   0      0.005(| 0.005(|   | 36)  | 36) 1.8 4.25sin       | | | 36  | 36   | 36 |    且 25 25      且   (3-40) P%时间概率的降雨衰减为 A p  0.01( A P 0.01 )  [0.655 0.033ln(  P ) 0.045ln(  A 0.01 )   (1  P )sin ]  (3-41)