datalab实验报告.pdf

发布时间：2022-06-10 发布人：admin 分类：说明书资料大小：0.61M 资料格式：pdf 举报版权申诉

qq_43496675-12505812-16359647386399389427.pdf-第1页.png

第1页 / 共12页

qq_43496675-12505812-16359647386399389427.pdf-第2页.png

第2页 / 共12页

qq_43496675-12505812-16359647386399389427.pdf-第3页.png

第3页 / 共12页

qq_43496675-12505812-16359647386399389427.pdf-第4页.png

第4页 / 共12页

qq_43496675-12505812-16359647386399389427.pdf-第5页.png

第5页 / 共12页

qq_43496675-12505812-16359647386399389427.pdf-第6页.png

第6页 / 共12页

qq_43496675-12505812-16359647386399389427.pdf-第7页.png

第7页 / 共12页

qq_43496675-12505812-16359647386399389427.pdf-第8页.png

第8页 / 共12页

文本预览

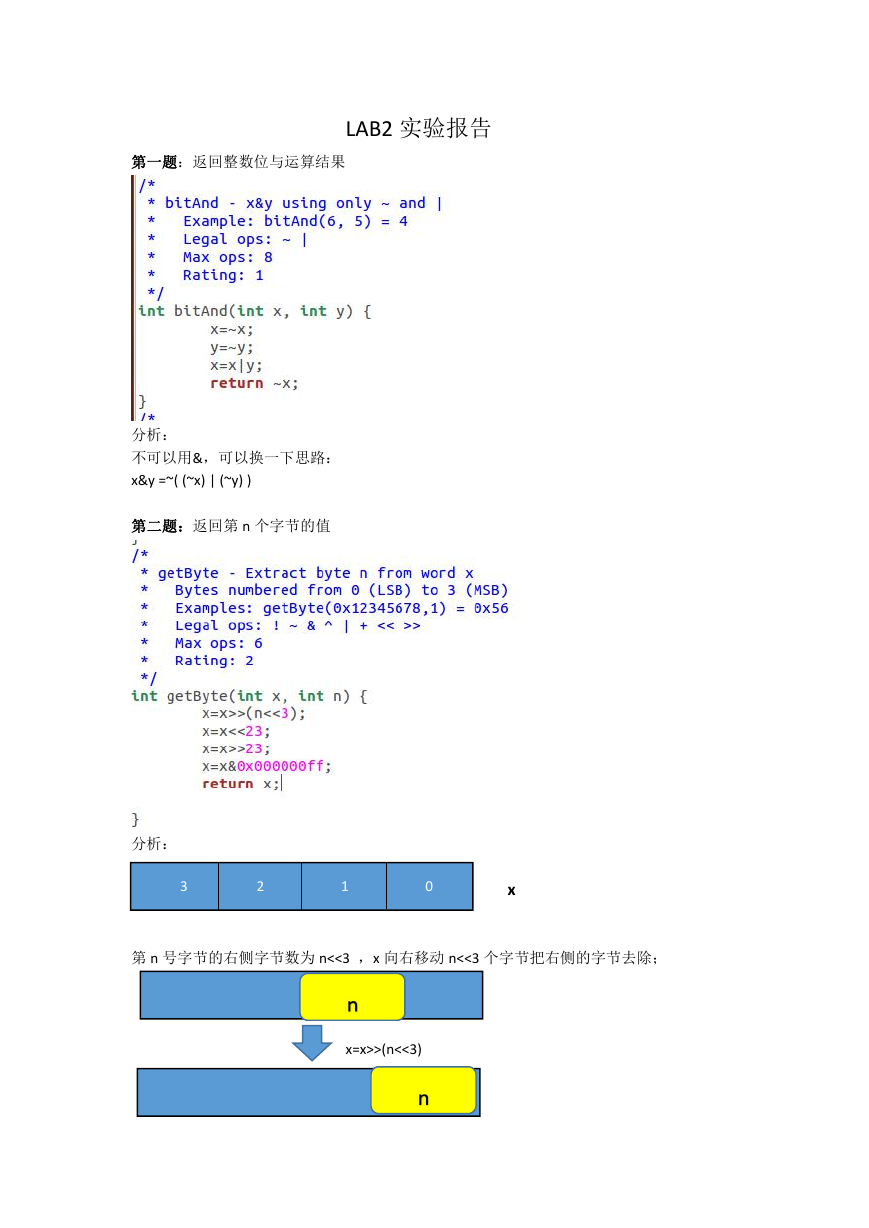
第一题：返回整数位与运算结果 LAB2 实验报告分析：不可以用&，可以换一下思路： x&y =~( (~x) | (~y) ) 第二题：返回第 n 个字节的值分析： 3 2 1 0 x 第 n 号字节的右侧字节数为 n<<3 ，x 向右移动 n<<3 个字节把右侧的字节去除； x=x>>(n<<3)

X<<23 除去左侧字节 X>>23 回到最低位 xxxxxxx…………………………x X&=0x000000ff 将左侧的符号扩展位置 0 000000…………………………0 3. 第三题：实现逻辑右移 ①因为机器进行算术右移所以要处理右移后的符号扩展位，将其置 0 ，可以令其与 0x00…… 01……1 类似的数进行位与运算，其中 0 有 n 个. ②获得 0x0……01……1: Ⅰ.1<<31 得到 0x80000000 Ⅱ.=> 向右移动 n-1 位 >>n<<1 Ⅲ.=>取反~ 最终：（~（0x01<<31>>n<<1））&x

4. 第四题：得到二进制数里的位 1 的个数分析：由于只可以使用运算最多 40 次，如果一位一位地计算的话，需要处理 32 位，平均每一位至少处理次数>2 ，因此这种方法显然不行，考虑另外一种方法： Eg: 01 11 00 01 1 2 0 1 3 1 4 类似于递归的反向过程：将目标字段一分为二，分别计算两个字段的 bit 1 个数，相加得到结果。 L=0101 0101 & 01 11 00 01 = 01 01 00 01 x>>1 = 00 11 10 00 R=0101 0101 & 00 11 10 00 = 00 01 00 00 x=L+R= 01 10 00 01 (1 2 0 1) L=0011 0011 & 01 10 00 01 = 00 10 00 01 x>>2 = 00 01 10 00 R=0011 0011 & 00 01 10 00 = 00 01 00 00 x=L+R = 0011 0001 （3 1 ） L=0000 1111 & 0011 0001 =0000 0001 x>>4 = 0000 0011 R=0000 1111 & 0000 0011 = 0000 0011

x = L+R =00000100 (4) 通过位操作得到：r1=0x55555555 r2=0x33333333 r4=0x0f0f0f0f r8=0x00ff00ff r16=0x0000ffff 与上例类似： ①l = x&r_n 每一子字段的左半部分组成（左子字段 1 的个数） ②r = (x>>1)&r_n 每一字段的右半部分组成（右子字段 1 的个数） ③x = l+r 每一字段的左右半字段的和（子字段 1 的个数） 5. 第五题：返回! x 即，当 x 为 0 的时候返回 1，否则返回 0 ①如何判断 x 是否为 0？  注意 0 的补码为 0  如果一个数不是 0，例如一个 8 位数 00110010，补码 x’=11001110，x ^ x’ = 11111100 结果一般不为全 0，而且特点是第一位不为 0，（x ^ x’）>>31 = 11111111  除了一个特殊的数 x=10000000， x’ = 10000000 , ②所以可以这样表达一个数非 0：( ( x ^ ( (~x)+1 ) )>>31 ) + x >>31（即数 x 与它的补码 x’位异或后得到的数第一位为 1，或者不满足前一个条件，但是数 x 的第一位为 1） ③当 x 为 0 的时，x=00000000,当 x!=0 时，x=11111111 ，如果要让 x=0 时返回 1，则可以 return *+(~temp)&1 x ^ x’ = 00000000

6. 第六题：返回补码表示的最小整数分析：补码表示的最小整数为符号位为 1，其余为为 0 的整数，即：-2^(w-1) 即 1<<31 7.第七题：判断一个不骂表示的整数 x 是否可以用 n 个字节表示分析： ①我们知道一个带符号的整数进行位扩展后得到的数跟它是等价的，比如 8 位的数 10111000 位扩展为 16 位：1111111110111000，那么新增的每一位与原来的符号位相同。 ②反过来，如果要将一个 16 位的数，缩小成为一个 8 位的数，只需要这个 16 位的数的高 9 位相同（全为 0 或者全为 1） ③解题步骤：  取高 32-n+1 位： n = 32 + (~n) +1 get = ((1<<31)>>n) & x  根据符号位构造高 n+1 位需要满足的数： s = ( (1<<31) & x )>>n

 将两个数异或，如果结果为全 0 表示 x 满足条件，可以位压缩至 n 位：这里可以用前一个题目判断一个数为 0 的方法（而且因为第一位都等于符号位因此不会出现结果第一位为 1 的情况）： get = get ^ s , get = ( get ^ ( (~ get) +1) )>>31 , return get&1 8.第八题：计算 x/(2^n) ,向 0 舍入分析： ①x/ (2^n) 实际上就是，将 x 右移 n 位，但是要判断是否舍入 ②向 0 舍入：先取得 x 的后 n 位，如果 x 大于 0，符号位 s 为 0，则舍去，如果 x 大于 0，符号位 s 为 1 则结果+1 ②解题步骤：  取低 n 位：bias = ~(1<<31>>31<>31  根据符号判断是否在右移后进位： return (x>>n) + ( (x>>31) &bias&1 ) 9. 第九题：返回一个补码数的相反数

分析：补码数的相反数就是它的补码：（~x）+1 10. 第十题：判断一个补码整数是否为正数，是返回 1 否则返回 0 分析： ①正数==不是 0&不是负数 ②不是 0：利用判断是否为 0 的方法，这个题目里面也不需要排除 100……0 的情况，因为负数也不满足为 1 的条件： temp = ( ③不是负数：~(x>>31) ④结果：（temp&(~(x>>31))）&1 ^ ( (~x)+1 ) x )>>31; 11. 第十一题：判断 x<=y 分析： ①可以将 x-y 的结果和 x,y 的符号一起考虑，进行判断 ②最简单的是符号不同&&x 是负数 ③x-y >=0  S_x 和 s_y 相同：x>=y  S_x 和 s_y 不同&&s_x = 1(负溢出): xy

⑤再判断结果是不是 0 解题步骤：  得到 s_x = x>>31 , s_y = y>>31 ,和 differ_s = s_x^ s_y  得到 minus = x-y = x+ (~y) +1，得到 x-y 的符号：s_m= minus>>31  判断 0： zero =~((minus^ ( ( ~minus)+1 ) )>>31)  1.~(differ_s&s_y): 不是 y 为负，x 为正，排除了正溢出  2. (differ_s&s_x):  3. s_m |zero : 结果为负，或者结果为 0  结果：在没有正溢出的情况下：结果为负，或者结果为 0，或者 x 负 y 正  return 1&（(~(differ_s&s_y)) & ((~(differ_s&s_x)) |s_m |zero ) ） x 为负，y 为正，排除了负溢出 12. 第十二题：求 log2(x) x>0 x 是整数分析：只需判断最高位的权值，因为限制了运算次数最多 90 次，使用一点小技巧：二分法例如 1：0x 03f8 a102 ①0xffff0000&x = 0x03f80000>0 所以至少权值有 4 ,result+=4 = 4 ,继续考察前 4 位 x>>4=0x03f8 ②0x0000ff00&x = 0x0300>0 所以权值至少可以再加 2 ,result+=2 = 6,继续考察前位 x>>2 = 0x03，前 1 位是符号位，不考查，结果就是 result=6 例如 2：0x0300 ①0xffff0000&x =0 所以不用移位,考察后 4 位的前 2 位 ②0x0000ff00&x = 0x0300 >0 result+=2 =2 继续考察前 2 位的第一位, x>>2 = 0x03 ③0x000000f0&x=0 因此 result=2 以 8 位为例图解：result=0; 前 4 位①>0? result+=4 ,x>>4 ②==0?下一次考察后 4 位

分享到：

赞收藏

资料库

datalab实验报告.pdf

相关推荐

课程资源

热门标签

最新资料