logo资料库

太原理工大学AI实验报告.docx

发布时间：2022-06-02 发布人：admin 分类：说明书 资料大小：0.37M 资料格式：docx 举报 版权申诉
第1页 / 共24页
第2页 / 共24页
第3页 / 共24页
第4页 / 共24页
第5页 / 共24页
第6页 / 共24页
第7页 / 共24页
第8页 / 共24页
资料共24页，剩余部分请下载后查看
    实验报告☑ 实践报告□ 课程名称： 人工智能基础R 实验、实践名称： 人工智能基础R 实验 实验、实践地点： 线上 专业班级： 学号： 学生姓名： 指导教师： 2020年 05 月 22 日 1
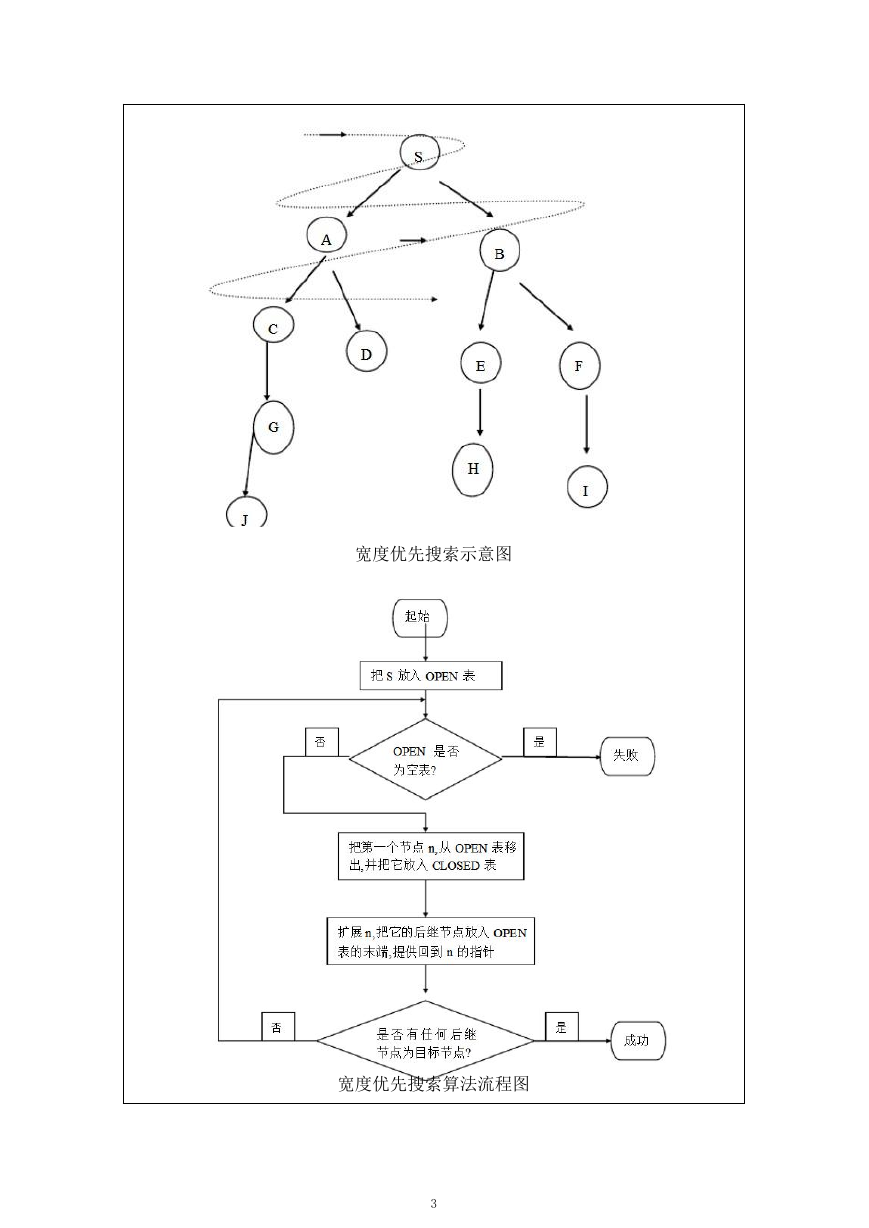
    实验名称 实验一 盲目搜索算法（宋体，四号，加粗） 实验地点 线上 实验时间 2020.5.21 一、实验目的和要求 掌握盲目搜索算法之一的宽度优先搜索求解算法的基本思想。对于宽度优 先搜索算法基本过程，算法分析有一个清晰的思路，了解宽度优先搜索算法在 实际生活中的应用。（宋体，小四号，全文英文使用 Times New Roman） 二、实验内容和原理 宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一 算法也是很多重要的图的算法的原型。 其基本思想是: (1) 把起始节点放到 OPEN 表中(如果该起始节点为一目标节点,则求得一个 解答)。 (2) 如果 OPEN 是个空表,则没有解,失败退出;否则继续。 (3) 把第一个节点(节点 n)从 OPEN 表移出,并把它放入 CLOSED 扩展节点 表中。 (4) 扩展节点 n。如果没有后继节点,则转向上述第(2)步。 (5) 把 n 的所有后继节点放到 OPEN 表的末端,并提供从这些后继节点回到 n 的指针。 (6) 如果 n 的任一个后继节点是个目标节点,则找到一个解答,成功退出;否则 转向第(2)步。 三、主要仪器设 备 笔记本电脑、Dev C++编译环境 四、操作方法和实验步骤 1.分析算法基本原理和基本流程； 2.确定对问题描述的基本数据结构，如 Open 表和 Closed 表等； 3.编写程序并调试成功； 4.撰写实验报告。 2
    宽度优先搜索示意图 宽度优先搜索算法流程图 3
    from collections import deque # 线性表的模块 # 首先定义一个创建图的类，使用邻接矩阵 class Graph(object): def __init__(self, *args, **kwargs): self.order = [] # visited order self.neighbor = {} def add_node(self, node): key, val = node if not isinstance(val, list): print('节点输入时应该为一个线性表') self.neighbor[key] = val # 避免不正确的输入 # 首先判断根节点是否为空节点 if root != None: search_queue = deque() search_queue.append(root) visited = [] # 宽度优先算法的实现 def BFS(self, root): else: print('root is None') return -1 while search_queue: person = search_queue.popleft() self.order.append(person) if (not person in visited) and (person in self.neighbor.keys()): search_queue += self.neighbor[person] visited.append(person) def clear(self): self.order = [] def node_print(self): for index in self.order: print(index, end=' ') 4
    if __name__ == '__main__': # 创建一个二叉树图 g = Graph() g.add_node(('S', ['A', 'B'])) g.add_node(('A', ['C', 'D'])) g.add_node(('B', ['E', 'F'])) g.add_node(('C', ['G'])) g.add_node(('G', ['J'])) g.add_node(('E', ['H'])) g.add_node(('F', ['I'])) # 进行宽度优先搜索 g.BFS('S') print('宽度优先搜索:') print(' ', end=' ') g.node_print() g.clear() 五、实验数据记录和处理 5
    六、实验结果与分析 按照BFS遍历该图的过程如下：首先，将初始结点s设置为第0层，然后找出结点s 的所有邻居结点，其中还没有被遍历到的结点就将它们作为第1层的结点。再找 出第1层的结点的邻居结点，所有未遍历的结点作为第2层的结点。依次遍历完图 中所有结点，可得BFS的流程为： ·将源点置为第0层 ·从源点s到该第i层每一个结点需要经过i条边 ·第i层的每一个结点均来自前一层i-1。i为层数索引 宽度优先搜索算法(Breadth First Search，BSF)，思想是： · 1.从图中某顶点v出发，首先访问定点v · 2.在访问了v之后依次访问v的各个未曾访问过的邻接点； · 3.然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点 的邻接点先于后被访问的顶点的邻接点被访问; · 4.直至图中所有已被访问的顶点的邻接点都被访问到; · 5.如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新 的起始点，重复上述过程，直至图中所有顶点都被访问到为止。 换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有 路径相通且路 径长度为1,2...的顶点。 如上图的BFS访问顺序为： S -> A -> B -> C ->D -> E -> F -> G -> H -> I -> J 七、讨论、心得 6
    实验名称 实验二 启发式搜索算法 实验地点 线上 实验时间 2020.5.25 一、实验目的和要求 1.加深对各种状态图搜索策略概念的理解； 2.熟悉和掌握 A*搜索的定义、估价函数和算法过程 3.理解和掌握 A*搜索过程，能够用选定的编程语言求解八数码问题，理解 求解流程和搜索顺序； 4.通过实验掌握估价函数的计算方法，理解估价函数定义的意义。 二、实验内容和原理 A*(A-Star)算法是一种启发式搜索方法，目前在网络路由算法、机器人探路、 人工智能、游戏设计等方面有着普遍的应用。 A*算法一般是以估价函数 的大小来排列待扩展状态的次序，每次选择 f(n) 值最小者进行扩展。 f(n)=g(n)+h(n) 其中g(n) 是初始结点到n结点的实际代价，而h(n)是从n结点点到目的结点的最 佳路径的估计代价，且h(n)<=h*(n), h*(n)为n结点到目的结点的最优路径的代 价。 保证找到全局最优解的条件，关键在于估价函数h(n)的选取： 估价值h(n)小于等于n结点到目标结点最优路径的距离实际值，这种情况下， 搜索的点数多，搜索范围大，效率低，但能得到全局最优解。 如果估价值h(n)大于实际值, 搜索的点数少，搜索范围小，效率高，但不能保 证得到全局最优解。 估价值与实际值越接近，估价函数取得就越好。 三、主要仪器设 备 笔记本电脑 四、操作方法和实验步骤 请下载并安装附件（智能搜索算法教学软件.rar）里的智能搜索算法教学实 7
    验系统，然后点击 A*算法进行仿真实验。 实验要求如下： 1. 单击"A*算法介绍"，回顾 A*算法的基本原理。 2. 在"A*算法演示程序"中，选择"自动寻路问题演示"进行仿真实验： 2.1 设置起点、终点和墙：选中“起点”并单击某一方格可设置起点，选中 “终点”并单击某一方格可设置终点，选中“墙”并单击若干个方格可设置墙，若 单击“重置”则清除所有的设置。 2.2 运行 A*算法：单击“开始”，可以看到起点的实际代价 g（搜索深度， 即搜索步数）、估计代价 h（起点到终点的哈密尔顿距离，即起点到终点的横 向和纵向的方格数之和）和估价函数值 f（f=g+h），然后依次单击若干次“下一 步”后，可以看到有深蓝色边框的方格为当前正扩展的状态节点，天蓝色的方格 为 open 表中待扩展的状态节点，灰色的方格为放入 closed 表的已扩展的状态节 点，一直到搜索到终点为止，或者单击“继续”直接搜索到终点。如果单击“重 置”则重新按照 2.1 和 2.2 重新进行实验。 2.3 结果记录：请拍照上传搜索到终点的实验结果图，并记录 A*算法扩展 的节点数，分析起点和终点的实际代价 g 或估计代价 h 有什么特点，以及搜索 过程中估价函数值 f 有什么特点？ 3.在"A*算法演示程序"中，选择"8 数码问题演示"进行实验： 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料