表上作业法.pdf-资料库

See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/266911500 A Improved Vogel's Approximatio Method for the Transportation Problem Article in Mathematical and Computational Applications · August 2011 DOI: 10.3390/mca16020370 CITATIONS 12 2 authors: READS 660 Serdar Korukoğlu Ege University Serkan Balli Mugla Üniversitesi 49 PUBLICATIONS 383 CITATIONS 45 PUBLICATIONS 118 CITATIONS SEE PROFILE SEE PROFILE Some of the authors of this publication are also working on these related projects: Tabakalı Kompozit Plaklardaki Hasar Durumunun Yapay Zeka Teknikleri ile Analiz Edilmesi View project All content following this page was uploaded by Serkan Balli on 30 October 2015. The user has requested enhancement of the downloaded file.

Mathematical and Computational Applications, Vol. 16, No. 2, pp. 370-381, 2011. © Association for Scientific Research Aҭ IMPROVED VOGEL’S APPROXIMATIOҭ METHOD FOR THE TRAҭSPORTATIOҭ PROBLEM 1Department of Computer Engineering, Ege University, 35000, Bornova, Đzmir, Turkey Serdar Korukoğlu1 and Serkan Ballı2 2Department of Statistics, Muğla University, 48187, Muğla, Turkey serdar.korukoglu@ege.edu.tr serkan@mu.edu.tr Abstract- Determining efficient solutions for large scale transportation problems is an important task in operations research. In this study, Vogel’s Approximation Method (VAM) which is one of well-known transportation methods in the literature was investigated to obtain more efficient initial solutions. A variant of VAM was proposed by using total opportunity cost and regarding alternative allocation costs. Computational experiments were carried out to evaluate VAM and improved version of VAM (IVAM). It was seen that IVAM conspicuously obtains more efficient initial solutions for large scale transportation problems. Performance of IVAM over VAM was discussed in terms of iteration numbers and CPU times required to reach the optimal solutions. Keywords- Transportation Problem, Integer Programming, Vogel’s Approximation Method, Total Opportunity Cost, Simulation Experiments 1. IҭTRODUCTIOҭ The transportation problem is a special kind of the network optimization problems. It has the special data structure in solution characterized as a transportation graph. Transportation models play an important role in logistics and supply chains. The problem basically deals with the determination of a cost plan for transporting a single commodity from a number of sources to a number of destinations [16]. The purpose is to minimize the cost of shipping goods from one location to another so that the needs of each arrival area are met and every shipping location operates within its capacity [10]. Network model of the transportation problem is shown in Figure 1 [17]. It aims to find the best way to fulfill the demand of n demand points using the capacities of m supply points. Cij Supplies available S1 S2 S3 Sm . . . D1 D2 D3 Dn . . Demand requirements Figure 1. Network model of the transportation problem

S. Korukoğlu and S. Ballı 371 ijx is number of In Figure 1, S1-Sm are sources and D1-Dn are destinations. units shipped from supply point i to demand point j then the general linear programming representation of a transportation problem is : ijc is cost and m n min ∑ ∑ c x ij ij 1 = i 1 = j n subject to ≤∑ S x ij (i=1,2,...,m) Supply constraints (1) i 1 = j n ≥∑ x D ij j (j=1,2,...,n) Demand constraints (2) 1 = j ijx ≥ 0 and integer for all i,j If total supply equals total demand then the problem is said to be a balanced transportation problem. The reader may refer to Wagner [17] and Taha [16] for detailed coverage of transportation problem. Transportation problems can be solved by using general simplex based integer programming methods, however it involves time-consuming computations. There are specialized algorithms for transportation problem that are much more efficient than the simplex algorithm [18]. The basic steps to solve transportation problem are: Step 1. Determination the initial feasible solution, Step 2. Determination optimal solution using the initial solution. In this study, basic idea is to get better initial solutions for the transportation problem. Therefore, study focused on Step 1 above. Several heuristic methods are available to get an initial basic feasible solution. Although some heuristics can find an initial feasible solution very quickly, oftentimes the solution they find is not very good in terms of minimizing total cost. On the other hand, some heuristics may not find an initial solution as quickly, but the solution they find is often very good in terms of minimizing total cost [2]. Well-known heuristics methods are North West Corner [4], Best Cell Method, Vogel’s Approximation Method (VAM) [11], Shimshak et. al.'s version of VAM [14], Goyal's version of VAM [6], Ramakrishnan's version of VAM [9] etc. Kirca and Satir [7] developed a heuristic to obtain efficient initial basic feasible solutions, called Total Opportunity-cost Method (TOM). Balakrishnan [3] proposed a modiﬁed version of VAM for unbalanced transportation problems. Gass [5] reviewed various methods and discussed on solving the transportation problem. Sharma and Sharma [12] proposed a new procedure to solve the dual of the well-known uncapacitated transportation problem. Sharma and Prasad [13] proposed heuristic gives significantly better solutions than the well-known VAM. This is a best heuristic method than Vogel’s to get initial solution to uncapacitated transportation problem. Adlakha and Kowalski [1] presented a simple heuristic algorithm for the solution of small fixed-charge transportation problems. Mathirajan and Meenakshi [8] were extended TOM using the VAM procedure. They coupled VAM with total opportunity cost and achieved very efficient initial solutions.

An Improved Vogel’s Approximation Method 372 In this paper, VAM was improved by using total opportunity cost and regarding alternative allocation costs. Mathirajan and Meenakshi [8] applied VAM on the total opportunity cost matrix. In addition to this method, improved VAM (IVAM) considers highest three penalty costs and calculates alternative allocation costs in VAM procedure. Then it selects minimum one of them. Paper is organized as follows. VAM is summarized and illustrated with solving a sample transportation problem in the following section. IVAM is explained in the third section. In the fourth section, simulation experiments are given and performance of IVAM over VAM is discussed. Results are clarified in fifth section. 2. VOGEL’S APPROXIMATIOҭ METHOD (VAM) VAM is a heuristic and usually provides a better starting solution than other methods. Application of VAM to a given problem does not guarantee that an optimal solution will result. However, a very good solution is invariably obtained with comparatively little effort [15]. In fact, VAM generally yields an optimum or close to optimum starting solution for small sized transportation problems [16]. VAM is based on the concept of penalty cost or regret. A penalty cost is the difference between the largest and next largest cell cost in a row or column. VAM allocates as much as possible to the minimum cost cell in the row or column with the largest penalty cost. Detailed processes of VAM are given below: Step 1: Balance the given transportation problem if either (total supply>total demand) or (total supply

S. Korukoğlu and S. Ballı 373 Table 1. An example of 5x5 transportation problem From/To D1 D2 D3 D4 D5 Supply S1 S2 S3 S4 S5 46 12 35 61 85 74 75 199 81 60 9 6 4 44 14 28 36 5 88 25 99 48 71 9 79 Demand 278 60 461 116 1060 461 277 356 488 393 Initial basic solution for this problem was obtained using VAM and given in Table 2. Using the values in Table 2, initial cost was calculated as 68804. Table 2. Initial solution tableau of VAM From/To D1 D2 D3 D4 D5 Supply S1 S2 S3 S4 S5 46 12 35 61 85 1 74 60 9 68 28 99 332 461 277 75 199 81 60 6 4 44 14 393 36 5 88 25 116 48 71 9 79 240 488 277 356 488 393 Demand 278 60 461 116 1060 Optimal solution was achieved using transportation simplex algorithm [4] within five iterations and final cost was found as 59356. Optimal solution tableau is given in Table 3. Solution of proposed method (IVAM) for the same problem is illustrated in the following section. Table 3. Optimal solution tableau From/To D1 D2 D3 D4 D5 Supply S1 S2 S3 S4 S5 46 12 35 61 85 277 1 74 75 199 81 60 60 9 6 4 44 14 461 28 36 5 88 25 116 99 48 71 9 79 239 488 333 461 277 356 488 393 Demand 278 60 461 116 1060

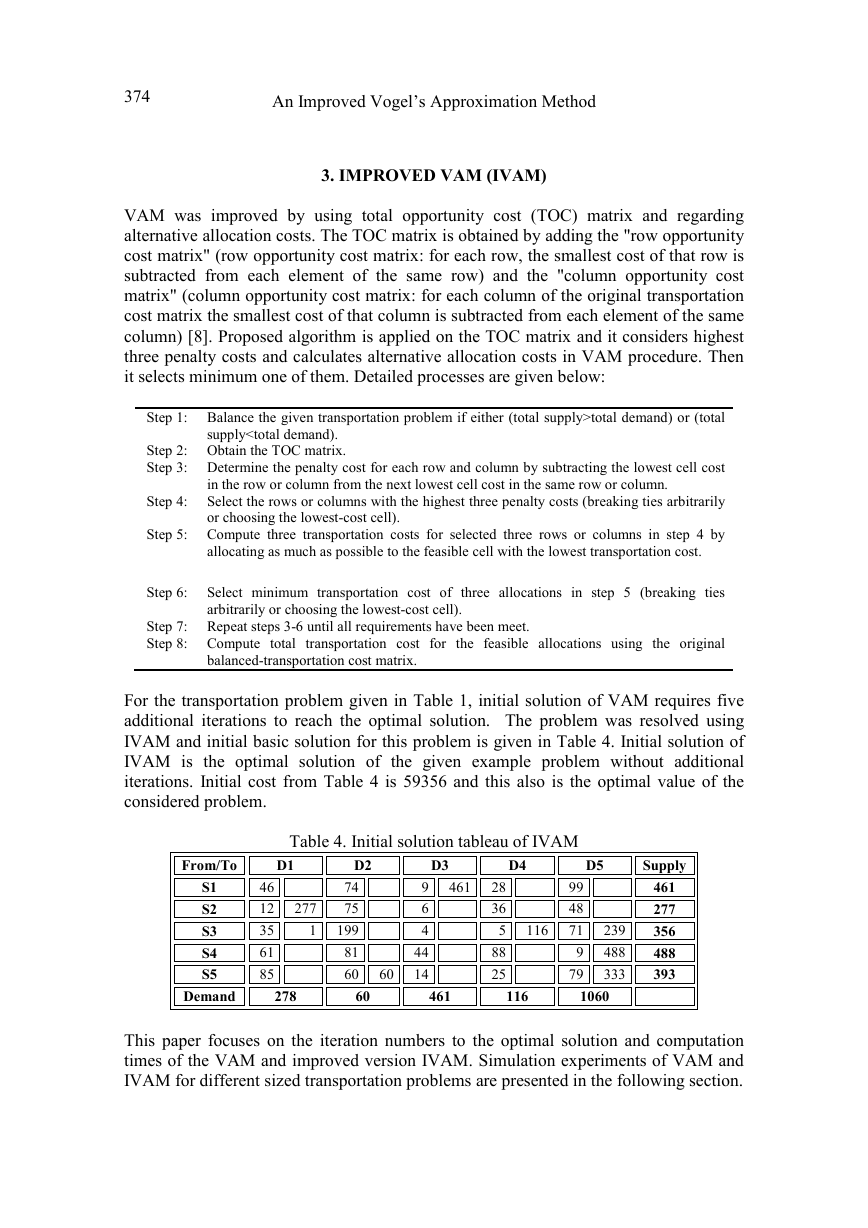
An Improved Vogel’s Approximation Method 374 3. IMPROVED VAM (IVAM) VAM was improved by using total opportunity cost (TOC) matrix and regarding alternative allocation costs. The TOC matrix is obtained by adding the "row opportunity cost matrix" (row opportunity cost matrix: for each row, the smallest cost of that row is subtracted from each element of the same row) and the "column opportunity cost matrix" (column opportunity cost matrix: for each column of the original transportation cost matrix the smallest cost of that column is subtracted from each element of the same column) [8]. Proposed algorithm is applied on the TOC matrix and it considers highest three penalty costs and calculates alternative allocation costs in VAM procedure. Then it selects minimum one of them. Detailed processes are given below: Step 1: Balance the given transportation problem if either (total supply>total demand) or (total supply

S. Korukoğlu and S. Ballı 375 4. SIMULATIOҭ EXPERIMEҭTS For evaluating the performance of the VAM and its variant IVAM, simulation experiments were carried out on a 2.13 GHz Intel Core 2 Duo machine with 4096 MB RAM. The main goal of the experiment was to evaluate the effectiveness of the initial solutions obtained by VAM and IVAM by comparing them with optimal solutions. Effectiveness indicates closeness degree which is the lowest iteration number between initial solution and the optimal solution. Measures of effectiveness are explained below. 4.1 Measure of effectiveness The performances of VAM and IVAM are compared using the following measures: Average Iteration (AI): Mean of iteration numbers to obtain optimal solutions using the initial solutions of VAM and IVAM over various sized problem instances. ̱umber of best solutions (̱BS): A frequency which indicates the number of instances VAM and IVAM yielded optimal solution with lower iteration over the total of problem instances. NBS does not contain case of equal iteration between VAM and IVAM. Computation Time: The CPU time is represented by three variables: T1, T2 and T3. T1 is the time to reach initial solution. T2 is the time to reach optimal solution from initial solution and T3 is the total time from the beginning that is sum of T1 and T2. 4.2 Experimental design The transportation problems were randomly generated with twelve different sizes (row x column): 5x5, 10x10, 10x20, 10x30, 10x40, 20x20, 10x60, 30x30, 10x100, 40x40, 50x50 and 100x100, respectively. The performance of the VAM and IVAM were compared over 1000 problem instances for each different sized problem. Total problem instances were 12000. Costs were generated as uniformly discrete in the range of (0,1000) and supplies and demands were generated in the range of (0,100) uniformly discrete. All the 12000 problem instances were balanced. The experimental design was implemented using ANSI C. 4.3 Comparison of VAM and IVAM The experiments and the analysis of the experimental data are presented in this section. For each problem instance, a linear programming model was implemented and solved. In order to get a linear programming model for each problem instance, a matrix generator procedure and VAM and IVAM were implemented using ANSI C. For each problem instance, the heuristic solutions were obtained using VAM and IVAM. The performance of the VAM and IVAM in comparison with the optimal solution is presented below. 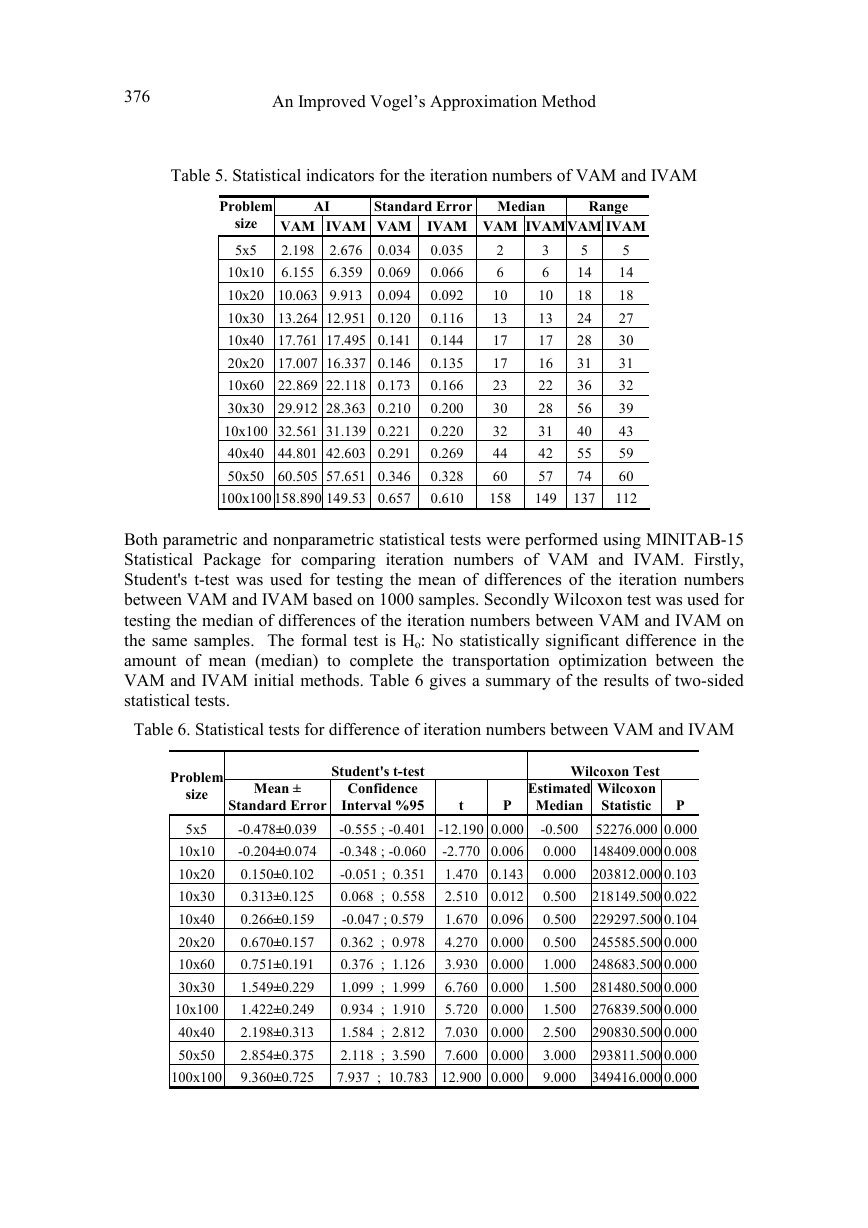Performance measure - AI: AI and other statistics for the iteration numbers of VAM and IVAM over various sized problems are given in Table 5. For each different sized problem, statistics are calculated using 1000 problem instances. From Table 5, it is seen that AI of VAM is better than IVAM for small sized transportation problems but it deteriorates when problem size increases. IVAM yields more efficient results than VAM for large sized problems.

An Improved Vogel’s Approximation Method 376 Table 5. Statistical indicators for the iteration numbers of VAM and IVAM Problem AI Standard Error Median Range size VAM IVAM VAM IVAM VAM IVAM VAM IVAM 2.198 2.676 0.034 5x5 10x10 6.155 6.359 0.069 10x20 10.063 9.913 0.094 10x30 13.264 12.951 0.120 10x40 17.761 17.495 0.141 20x20 17.007 16.337 0.146 10x60 22.869 22.118 0.173 30x30 29.912 28.363 0.210 10x100 32.561 31.139 0.221 40x40 44.801 42.603 0.291 50x50 60.505 57.651 0.346 100x100 158.890 149.53 0.657 0.035 0.066 0.092 0.116 0.144 0.135 0.166 0.200 0.220 0.269 0.328 0.610 2 6 10 13 17 17 23 30 32 44 60 158 5 3 14 6 18 10 24 13 28 17 31 16 36 22 56 28 40 31 55 42 74 57 149 137 5 14 18 27 30 31 32 39 43 59 60 112 Both parametric and nonparametric statistical tests were performed using MINITAB-15 Statistical Package for comparing iteration numbers of VAM and IVAM. Firstly, Student's t-test was used for testing the mean of differences of the iteration numbers between VAM and IVAM based on 1000 samples. Secondly Wilcoxon test was used for testing the median of differences of the iteration numbers between VAM and IVAM on the same samples. The formal test is Ho: No statistically significant difference in the amount of mean (median) to complete the transportation optimization between the VAM and IVAM initial methods. Table 6 gives a summary of the results of two-sided statistical tests. Table 6. Statistical tests for difference of iteration numbers between VAM and IVAM Problem size 5x5 10x10 10x20 10x30 10x40 20x20 10x60 30x30 10x100 40x40 50x50 100x100 Student's t-test Mean ± Standard Error Confidence Interval %95 t P Wilcoxon Test Wilcoxon Statistic Estimated Median P -0.478±0.039 -0.204±0.074 0.150±0.102 0.313±0.125 0.266±0.159 0.670±0.157 0.751±0.191 1.549±0.229 1.422±0.249 2.198±0.313 2.854±0.375 9.360±0.725 -0.555 ; -0.401 -12.190 0.000 -0.348 ; -0.060 -2.770 0.006 1.470 0.143 -0.051 ; 0.351 2.510 0.012 0.068 ; 0.558 -0.047 ; 0.579 1.670 0.096 4.270 0.000 0.362 ; 0.978 3.930 0.000 0.376 ; 1.126 1.099 ; 1.999 6.760 0.000 5.720 0.000 0.934 ; 1.910 7.030 0.000 1.584 ; 2.812 2.118 ; 3.590 7.600 0.000 7.937 ; 10.783 12.900 0.000 -0.500 52276.000 0.000 0.000 148409.000 0.008 0.000 203812.000 0.103 0.500 218149.500 0.022 0.500 229297.500 0.104 0.500 245585.500 0.000 1.000 248683.500 0.000 1.500 281480.500 0.000 1.500 276839.500 0.000 2.500 290830.500 0.000 3.000 293811.500 0.000 9.000 349416.000 0.000

资料库

表上作业法.pdf

相关推荐

数据库

热门标签

最新资料