随机信号处理上机作业.doc-资料库

catherine_zrr-9038281-4744302543356630251.doc.pdf-第1页.png

第1页 / 共11页

catherine_zrr-9038281-4744302543356630251.doc.pdf-第2页.png

第2页 / 共11页

catherine_zrr-9038281-4744302543356630251.doc.pdf-第3页.png

第3页 / 共11页

catherine_zrr-9038281-4744302543356630251.doc.pdf-第4页.png

第4页 / 共11页

catherine_zrr-9038281-4744302543356630251.doc.pdf-第5页.png

第5页 / 共11页

catherine_zrr-9038281-4744302543356630251.doc.pdf-第6页.png

第6页 / 共11页

catherine_zrr-9038281-4744302543356630251.doc.pdf-第7页.png

第7页 / 共11页

catherine_zrr-9038281-4744302543356630251.doc.pdf-第8页.png

第8页 / 共11页

随机信号处理作业姓名：张洳睿学号：113104000547 指导老师：顾红

题目：上机题 4 两个数据文件，第一个文件数据中只包含一个正弦波，通过 MATLAB 仿真计算信号频谱和功率谱来估计该信号的幅度,功率,归一化频率和相位?对第二个文件数据估计其中正弦波的幅度,功率和归一化频率？写出报告,包含理论分析,仿真程序及说明,误差精度分析等。第一文件调用格式 load FileDat01_1 s1,数据在变量 s1 中；第二文件调用格式 load FileDat01_2 s,数据在变量 s 中。 1、原理简介信号的数学表达式虽然有时可以详尽而确切地表示信号分解的结果，但往往不够直观。为了能既方便又明白地表示一个信号含有哪些频率分量，可对信号做傅里叶变换，将信号在时间域中的波形转变为频率域的频谱，进行频谱分析，进而可以对信号的信息作定量解释。对于离散时间序列，其频谱分析通常是对序列做离散傅里叶变换（DFT）。对一模拟信号 )(tx 进行采样，设采样点为 N ，可以得到一离散时间序列 [{ nx 0]},  Nn  1 ，对该序列做 N 点的离散傅里叶变化（DFT）为： ][ kx  1  N j e n  0 2  N nk ][ nx k  ,...,2,1,0 N  1 而 FFT 是一种 DFT 的高效算法，称为快速傅立叶变换。利用 DFT 中的周期性和对称性，可使整个 DFT 的计算变成一系列迭代运算，进而大幅提高运算速度，减少运算量。FFT 算法可分为按时间抽取算法和按频率抽取算法，这里就不再做阐述。对信号做 N 点的 FFT 运算后得到的序列，每一点的模值（除了第一个点）均 N 倍，而第一个点就是直流分量，其模值为直流分量的 N 倍。 2 为原始信号幅值的根据这一性质可以通过频谱图估计原信号的幅值。功率谱估计就是通过信号相关性估计出接收到信号的功率随频率变化的关系，主要研究信号在频域中的各种特征，目的是根据有限数据在频域内提取被淹没在噪声中的有用信号。传统的谱估计主要有两种方法：BT 法和周期图法。这里主要利用 BT 法，在 matlab 中编程实现求功率谱。 [ Nx BT 法就是利用信号的有限个观察值估计出自相关函数， ],0[ x ],... 1[ x ]1 然后根据维纳辛钦定理在（-M,M）区间上对自相关函数做傅里叶变换就可以得到功率谱，注意这里。通常采用有偏自相关函数估计（方差较小），公式为：  NM 1 mR xx ( ) mN    1 N n  0 1   mnxnx ()(  ) ，  Nm 1 (mRxx 称为取样自相关函数，是渐进一致估计，对上式进行傅氏变换，得到 BT )

M  ^ ) emR ( xx  jwm ，  NM 1 Mm  法的功率谱估计值为： ^ ( eP xx jw )  2、程序及结果分析 2.1 波形 1 （1）matlab 程序 clc; clear all; %清除所有变量 close all; %关闭所有打开的文件 load G:/FileDat01_1 s1; figure(1); plot(s1); title('信号的时域波形'); xlabel('t'); ylabel('幅度'); fs=1; N=length(s1); freq=linspace(-fs/2,fs/2,N); y=fftshift(fft(s1,N)); %将 fft 结果乘以 2 除以 N 得到的是真实的振幅 figure(2); subplot(2,1,1); plot(freq,abs(y/max(abs(y)))); title('信号的频域波形'); xlabel('频率'); ylabel('|幅度|'); subplot(2,1,2); plot(freq,abs(y/max(abs(y)))); axis([0,0.1,0,1.5]); title('将上图放大'); xlabel('频率'); ylabel('|幅度|'); grid on; a=fft(s1); [F,I]=max(abs(a)); % 对 S11 求相位 Amp=max(abs(y*2/N)); Ang=angle((a(I)))*180/pi; %%求功率谱 Y=xcorr(s1,'unbiased'); Y1=fftshift(fft(Y,N));

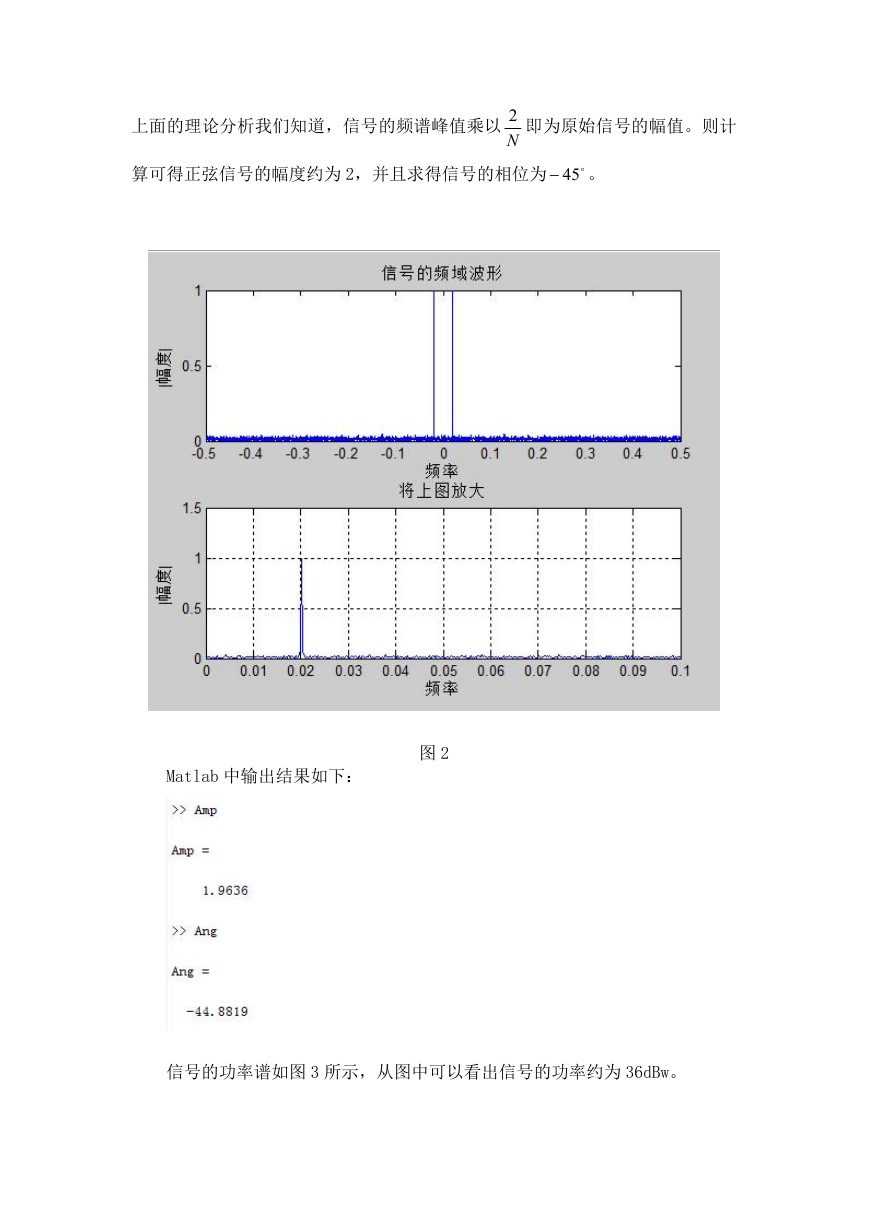
figure(3); subplot(2,1,1); plot(freq,10*log10(abs(Y1))); title('信号的功率谱'); xlabel('频率'); ylabel('功率谱/dB'); subplot(2,1,2); plot(freq,10*log10(abs(Y1))); axis([0,0.25,0,50]); title('将上图放大'); xlabel('频率'); ylabel('功率谱/dB'); grid on; （2）仿真结果及分析将文件 FileDat0_1 中的数据导入到 matlab 中，并作出信号的时域波形如图 1 所示。从图中可以看出原始信号为一加了噪声的正弦波形。图 1 信号的频域波形如图 2 所示。从图二中可以看出，在频率为 0.02 处出现一个峰值，由于这里的采样频率设置为 1Hz，所以信号的归一化频率就是 0.02。从

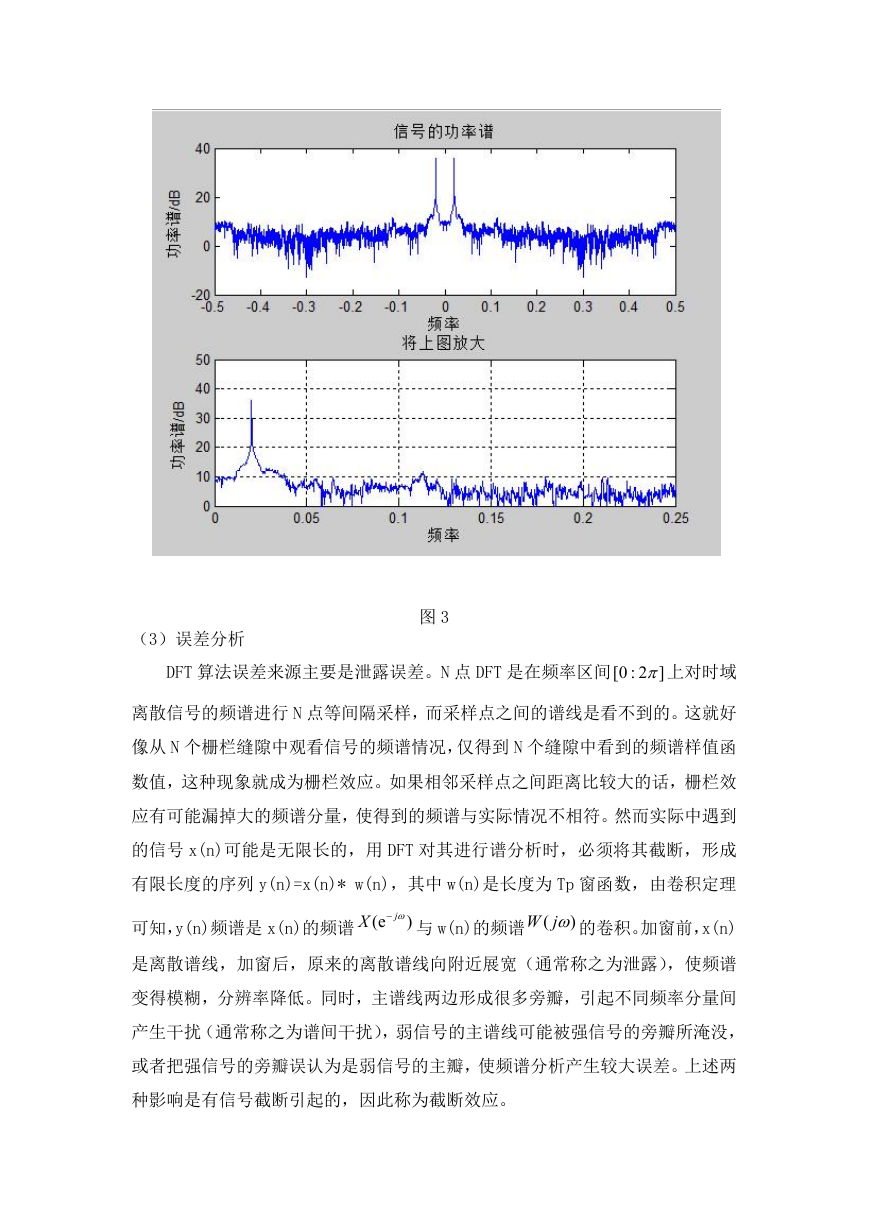
上面的理论分析我们知道，信号的频谱峰值乘以 2 即为原始信号的幅值。则计 N 算可得正弦信号的幅度约为 2，并且求得信号的相位为 45 。 Matlab 中输出结果如下：图 2 信号的功率谱如图 3 所示，从图中可以看出信号的功率约为 36dBw。

（3）误差分析图 3 DFT 算法误差来源主要是泄露误差。N 点 DFT 是在频率区间 ]2:0[  上对时域离散信号的频谱进行 N 点等间隔采样，而采样点之间的谱线是看不到的。这就好像从 N 个栅栏缝隙中观看信号的频谱情况，仅得到 N 个缝隙中看到的频谱样值函数值，这种现象就成为栅栏效应。如果相邻采样点之间距离比较大的话，栅栏效应有可能漏掉大的频谱分量，使得到的频谱与实际情况不相符。然而实际中遇到的信号 x(n)可能是无限长的，用 DFT 对其进行谱分析时，必须将其截断，形成有限长度的序列 y(n)=x(n)* w(n)，其中 w(n)是长度为 Tp 窗函数，由卷积定理可知，y(n)频谱是 x(n)的频谱 (e X )j  与 w(n)的频谱 ( W j 的卷积。加窗前，x(n) ) 是离散谱线，加窗后，原来的离散谱线向附近展宽（通常称之为泄露），使频谱变得模糊，分辨率降低。同时，主谱线两边形成很多旁瓣，引起不同频率分量间产生干扰（通常称之为谱间干扰），弱信号的主谱线可能被强信号的旁瓣所淹没，或者把强信号的旁瓣误认为是弱信号的主瓣，使频谱分析产生较大误差。上述两种影响是有信号截断引起的，因此称为截断效应。

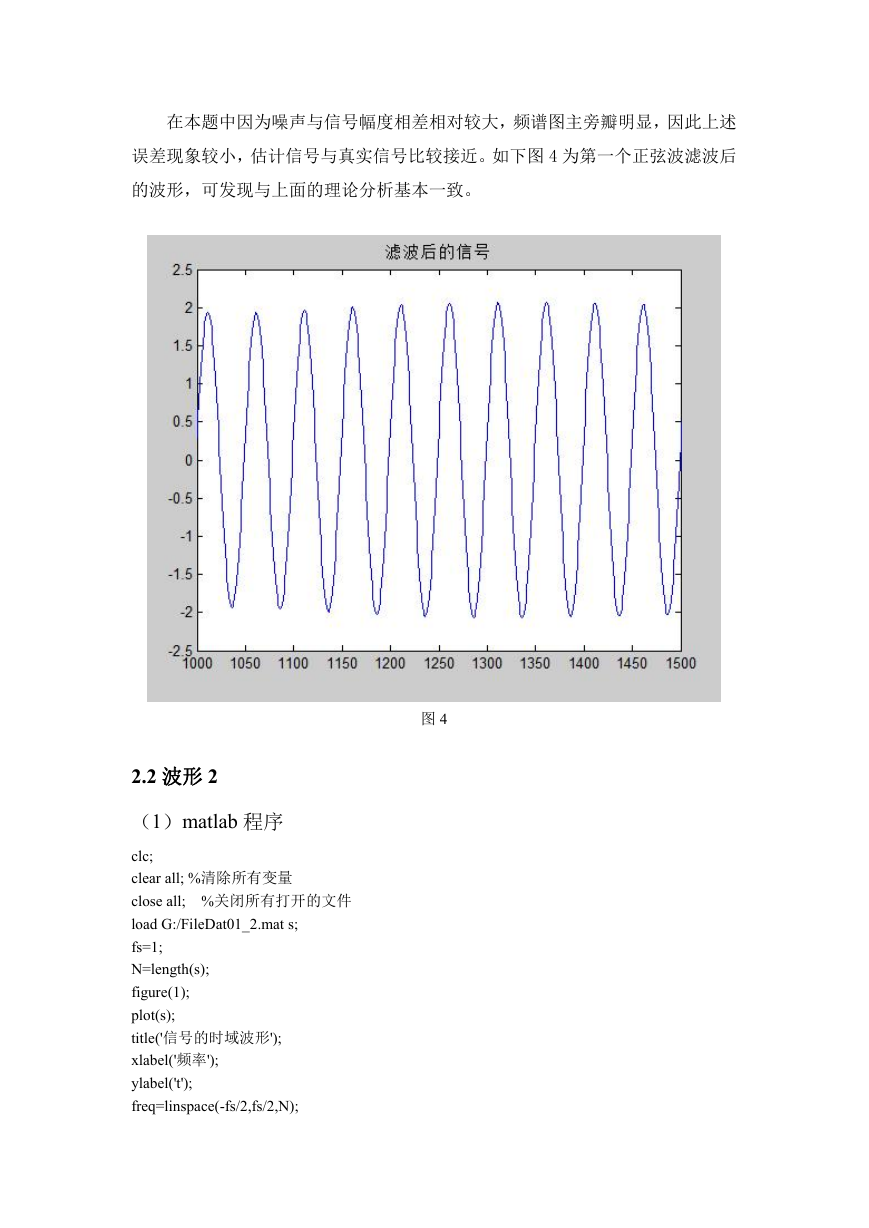
在本题中因为噪声与信号幅度相差相对较大，频谱图主旁瓣明显，因此上述误差现象较小，估计信号与真实信号比较接近。如下图 4 为第一个正弦波滤波后的波形，可发现与上面的理论分析基本一致。图 4 2.2 波形 2 （1）matlab 程序 clc; clear all; %清除所有变量 close all; %关闭所有打开的文件 load G:/FileDat01_2.mat s; fs=1; N=length(s); figure(1); plot(s); title('信号的时域波形'); xlabel('频率'); ylabel('t'); freq=linspace(-fs/2,fs/2,N);

y=fftshift(fft(s,N)); %将 fft 结果乘以 2 除以 N 得到的是真实的振幅 figure(2); subplot(2,1,1); plot(freq,abs(y/max(abs(y)))); title('信号的频域波形'); xlabel('频率'); ylabel('|幅度|'); subplot(2,1,2); plot(freq,abs(y/max(abs(y)))); axis([0,0.05,0,1.5]); title('放大后的波形'); xlabel('频率'); ylabel('|幅度|'); grid on; a=fft(s); Amp=max(abs(y*2/N)); Y=xcorr(s,'unbiased'); Y1=fftshift(fft(Y,N)); figure(3); subplot(2,1,1); plot(freq,10*log10(abs(Y1))); title('信号的功率谱'); xlabel('频率'); ylabel('功率谱/dB'); subplot(2,1,2); plot(freq,10*log10(abs(Y1))); axis([0,0.05,0,50]); title('将上图放大'); xlabel('频率'); ylabel('功率谱/dB'); grid on; （2）仿真结果及分析将文件 FileDat0_2 中的数据导入到 matlab 中，并作出信号的时域波形如图 5 所示。从图中可以看出原始信号为两个加了噪声的正弦波形。

资料库

随机信号处理上机作业.doc

相关推荐

课程资源

热门标签

最新资料