logo资料库

二维插值的基本算法及算例.ppt

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：1.04M 资料格式：ppt 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    数学实验之四 [1] 了解二维插值的基本原理，了解三种 网格节点数据的插值方法的基本思想； [2] 掌握用MATLAB计算二维插值的方 法，并对结果作初步分析； [3] 通过实例学习如何用插值方法解决实 际问题。 某山区的地形图 引例1：如何绘制山区地貌图 要在某山区方圆大约 27平方公里范围内修 建一条公路，从山脚出发经过一个居民区， 再到达一个矿区。横向纵向分别每隔 400米 测量一次，得到一些地点的高程： (平面区域 0<=x<=5600,0<=y<=4800) ，首先需作 出该山区的地貌图和等高线图。 1
    引例1：如何绘制山区地貌图 3600 3200 2800 2400 2000 1600 1200 1480 1500 1550 1510 1430 1300 1200 980 1500 1550 1600 1550 1600 1600 1600 1550 1500 1200 1100 1550 1600 1550 1380 1070 1500 1200 1100 1350 1450 1200 1150 1010 1390 1500 1500 1400 900 1100 1060 950 1320 1450 1420 1400 1300 700 900 850 1130 1250 1280 1230 1040 900 500 700 Y/x 1200 1600 2000 2400 2800 3200 3600 4000 2000 1500 Z 1000 500 0 0 5000 4000 3000 1000 2000 3000 1000 2000 Y 4000 5000 X 6000 0 y y                x 在某海域测得一些点 (x,y)处的水深z由下表给 出，船的吃水深度为 5英尺，在矩形区域（ 75，200） *（-50，150）里的哪些地方船要避免进入。 129 140 103.5 88 185.5 195 105 7.5 141.5 23 147 22.5 137.5 85.5 4 8 6 8 6 8 8 157.5 107.5 77 81 162 162 117.5 -6.5 -81 3 56.5 -66.5 84 -33.5 9 9 8 8 9 4 9 x y z x y z                二 维 插 值 的 提 法 第一种（网格节点） 已知 mn个节点 (xi, xj, zij) ( i=1, 2, …,m; j=1, 2, …, n ) 其中xi, yj互不相同，不妨设 a=x1
    二维插值的提法 二维插值的提法 y y3 y2 y1         (x*, y*)         x1 x2 x3 x4 x5 x 第二种（散乱节点） i i i 其中 已知n个节点 ( , , x y z ( , ) i yx 求任一插值点 .*z 处的插值 i () i  2,1 ,..., n ) 互不相同， )( ( x y , * *  ( , i yx i )) z  ,( yxf ), 通过全部已知节点 ,即 构造一个二元函数 ) ( xf i , ( 或 ( xf i y i , j  y i z  ij ,1,0  ) z  i , ; jm (  i ,1,0  ,1,0  ) , n ) n  * ). 再用 ),( yxf 计算插值，即 * z  * ( , yxf 网格节点插值法： 最邻近插值； 分片线性插值; 双线性插值； 双三次插值。 散点数据插值法： 修正Shephard法 y (x1, y2)  (x2, y2)   (x1, y1)   (x2, y1)           x 注意：最邻近插值一般不连续。具有连续性的最简 单的插值是分片线性插值。 y (xi, yj+1)  (xi+1, yj+1)   (xi, yj)  (xi+1, yj)            x 3
    四个插值点（矩形的四个顶点）处的函 数值： f (xi, yj)=f1， f (xi+1, yj)=f2， f (xi+1, yj+1)=f3， f (xi, yj+1)=f4 第一片(下三角形区域)： y  y x 1j  1i    y x j i x(  )x i  y j 插值函数为： f )y,x(f  1  f( 2  f 1 x)(  )x i  f( 3  f 2 y)(  )y j y     (x1, y2)  (x1, y1)   (x2, y2) (x2, y1)         x 双线性插值是一片一片的空间二次曲面构成。 插值函数的形式如下： ax( )y,x(f cy)(b )d    第二片(上三角形区域)：  1j   y  y x 1i  y x j i y)xx(   i i 插值函数为： f )y,x(f  1  f( 4  f 1 y)(  )y j  f( 3  f 4 x)(  )x i 注意：(x, y)当然应该是在插值节点所形成的矩形区 域内。显然，分片线性插值函数是连续的； 网格节点的插值计算； 散点数据的插值计算； 用MATLAB作插值计算小结 82 81 80 82 84 79 63 61 65 81 84 84 82 85 86            例：测得平板表面 3*5网格点处的温度 分别为：   x   y 试作出平板表面的温度分布曲面 z=f(x,y)的图形。 4
    二维插值:已有程序 z=interp2(x0,y0,z0,x,y,’method’) 被插值点 插值方法 插值 节点 被插值点 的函数值 Method可取： ‘nearest’ 最邻近插值；‘linear’ 双线性插 值； ‘cubic’ 双三次插值；缺省时 , 双线性插值。 注意：x0,y0为向量，但z0是矩阵，其 列数等于x0的长度，行数等于y0的长度。 xlabel('Width of Plate'), ylabel('Depth of Plate') zlabel('Degrees Celsius'), axis('ij'),grid, pause; zlin=interp2(width,depth,temps,wi,di,… 'cubic'); figure(3); mesh(wi,di,zlin) xlabel('Width of Plate'), ylabel('Depth of Plate') zlabel('Degrees Celsius'), axis('ij'),grid M文件 width=1:5; wenduqm.m depth=1:3; temps=[82 81 80 82 84;79 63 61… 65 81;84 84 82 85 86]; mesh(width,depth,temps);pause di=1:.1:3;di=di'; 加密数据点 wi=1:.1:5; zlin=interp2(width,depth,temps,… wi,di,'linear'); figure(2); mesh(wi,di,zlin); z=griddata(x0,y0,z0,x,y,’method’) 被插值点 的函数值 插值节点 被插值点 注意：x0,y0,z0均为向量，长度相等。 Method可取 ‘nearest’,’linear’,’cubic’,’v4’; ‘linear’是缺省值。 5
    分别用最近邻点插值、线性插值 和三次插值加密数据点，并分别作 出这三组数据点的网格图。 要在某山区方圆大约 27平方公里范围内修 建一条公路，从山脚出发经过一个居民区， 再到达一个矿区。横向纵向分别每隔 400米 测量一次，得到一些地点的高程： (平面区域 0<=x<=5600,0<=y<=4800) ，首先需作 出该山区的地貌图和等高线图。 注意观察双线性插值方法和双三 次插值方法的插值效果的差异。 4500 4000 3500 3000 2500 2000 1500 1000 500 4500 4000 3500 3000 2500 2000 1500 1000 500 0 0 2000 4000 0 0 2000 4000 6
    4200 4000 3800 3600 3400 3200 3000 2800 2600 Y 4200 4000 3800 3600 3400 3200 3000 2800 2600 Y 1500 2000 X 2500 1500 2000 X 2500 在某海域测得一些点 (x,y)处的水深z由下表给出， 船的吃水深度为 5英尺，在矩形区域（ 75，200）* （-50，150）里的哪些地方船要避免进入。 129 140 103.5 88 185.5 195 105 7.5 141.5 23 147 22.5 137.5 85.5 4 8 6 8 6 8 8 157.5 107.5 77 81 162 162 117.5 -6.5 -81 3 56.5 -66.5 84 -33.5 9 9 8 8 9 4 9 x y z x y z 假设：海底平滑 1.作出测量点的分布图； 2.求出矩形区域（ 75，200）*（-50，150）的 细分网格节点之横、纵坐标向量； 3.利用MATLAB中的散点插值函数求网格节点 的水深； 4.作出海底曲面图形和等高线图； 5.作出水深小于 5的海域范围。 clear; x=[129 140 103.5 88 185.5 195 105.5 157.5 107.5 77 81 162 162 117.5]; y=[7.5 141.5 23 147 22.5 137.5 85.5… -6.5 -81 3 56.5 -66.5 84 -33.5]; z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 … -9 -4 -9]; plot(x,y,'+'); pause 7
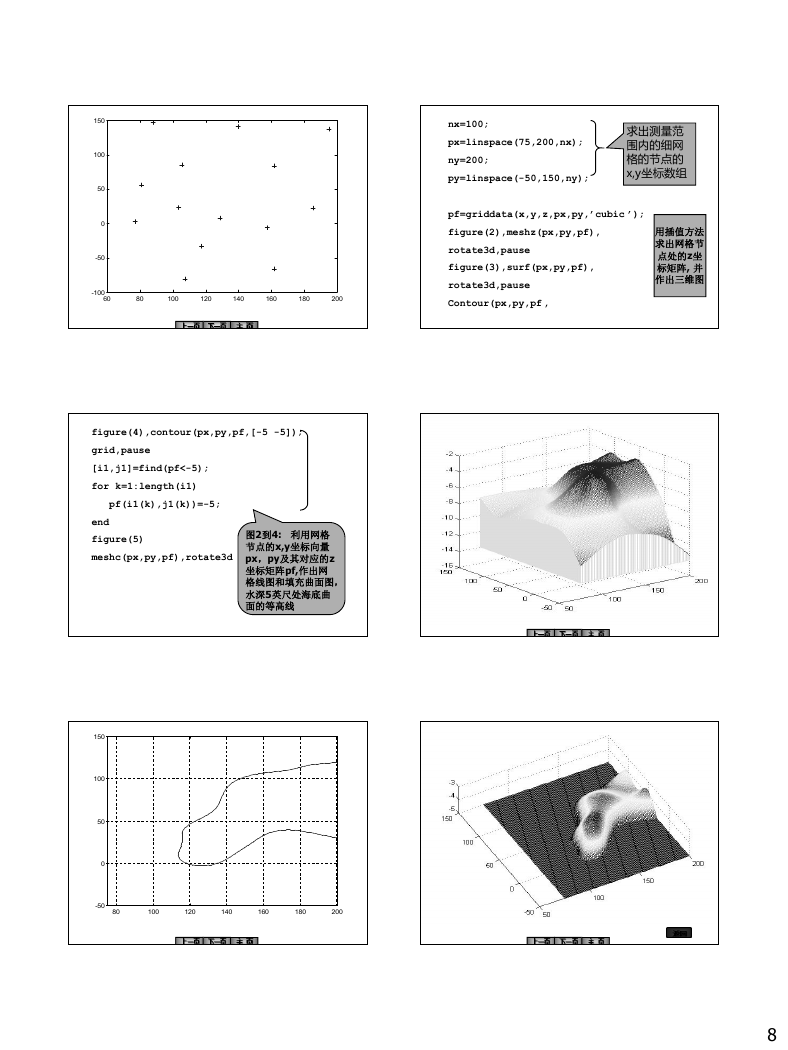
    nx=100; px=linspace(75,200,nx); ny=200; py=linspace(-50,150,ny); 求出测量范 围内的细网 格的节点的 x,y坐标数组 pf=griddata(x,y,z,px,py,’cubic ’); figure(2),meshz(px,py,pf), rotate3d,pause figure(3),surf(px,py,pf), rotate3d,pause Contour(px,py,pf, 用插值方法 求出网格节 点处的z坐 标矩阵, 并 作出三维图 150 100 50 0 -50 -100 60 80 100 120 140 160 180 200 figure(4),contour(px,py,pf,[-5 -5]); grid,pause [i1,j1]=find(pf<-5); for k=1:length(i1) pf(i1(k),j1(k))=-5; end figure(5) meshc(px,py,pf),rotate3d 图2到4: 利用网格 节点的x,y坐标向量 px，py及其对应的z 坐标矩阵pf,作出网 格线图和填充曲面图， 水深5英尺处海底曲 面的等高线 150 100 50 0 -50 80 100 120 140 160 180 200 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料