MIMO雷达发射波形优化设计.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：1.79M 资料格式：pdf 举报版权申诉

qq_36731567-11295924-4744302543287769557.pdf-第1页.png

第1页 / 共32页

qq_36731567-11295924-4744302543287769557.pdf-第2页.png

第2页 / 共32页

qq_36731567-11295924-4744302543287769557.pdf-第3页.png

第3页 / 共32页

qq_36731567-11295924-4744302543287769557.pdf-第4页.png

第4页 / 共32页

qq_36731567-11295924-4744302543287769557.pdf-第5页.png

第5页 / 共32页

qq_36731567-11295924-4744302543287769557.pdf-第6页.png

第6页 / 共32页

qq_36731567-11295924-4744302543287769557.pdf-第7页.png

第7页 / 共32页

qq_36731567-11295924-4744302543287769557.pdf-第8页.png

第8页 / 共32页

第一章绪论

1.1 MIMO雷达波形设计的研究意义及背景

1.2MIMO雷达波形设计研究现状的国内外背景和历史发展

第二章MIMO雷达概述

2.1 MIMO雷达的信号模型

一般信号模型

2.2 信号模型分类

第三章正交波形设计

3.1 正交波形的基本概念和定义

3.2 正交波形设计的意义

3.3 OFDM-LFM信号设计原理

OFDM-LFM信号模糊函数及波形

OFDM-LFM信号的模型为全部阵列单元发射彼此正交的线性调频信号,M个正交线性调频信号可通过图3来

3.4.1 遗传算法原理

3.4.2 使用普遍的几种代价函数和优化准则

第四章仿真结果及分析

4.1 OFDM-LFM波形设计与分析

4.2 遗传算法仿真结果及分析

4.3 序列二次规划算法

4.3.1 建立序列二次规划的数学模型

4.3.2 序列二次规划算法仿真结果及分析

第五章总结与展望

参考文献

附录

摘要 MIMO 雷达作为雷达技术领域的一个研究热点。按照系统的相关要求，MIMO 雷达的各个辐射单元能够发射不同且相互正交的信号波形，常用的比如正交多相编码信号，能够达到发射信号在空间形成低增益宽波束进而实现全空域探测的目标。MIMO 雷达的优势之一在于其可进行波形分集，所以它的关键技术部分即是设计具有比较低自相关旁瓣峰值（ASP）和互相关峰值（CP）的信号波形。本文首先建立出 MIMO 雷达的信号模型，对 MIMO 雷达的基本原理和收发通道矩阵的性质进行了分析。因为 OFDM 信号的每个波形能够分离，而且线性调频信号（LFM）具有大的时宽带宽积，可以同时提高雷达作用距离和距离分辨力，结合二者的特点，本文构建了 OFDM-LFM 信号模型，并通过信号模糊函数的分析验证了其理论上的正交性。随后采用同样具有良好脉冲压缩性能的多相编码信号，以极小化峰值旁瓣为代价函数选择通过遗传算法对发射波形进行优化。最后，基于序列二次规划研究了自相关峰值旁瓣电平和互相关峰值电平与码长 N、序列数 L 和加权系数的数值关系。关键词 MIMO 雷达，OFDM-LFM 信号，遗传算法，序列二次规划

ABSTRACT MIMO radar is a research hotspot in the field of radar technology.According to the relevant requirements of the system, each radiation unit of MIMO radar can transmit different and orthogonal signal waveforms, such as orthogonal polyphase coded signals, which can achieve the target of low gain wide beam in space formed by transmitting signals and then realize the detection in the whole airspace.The advantage of MIMO radar is that it can carry out waveform diversity, so its key technology is to design the signal waveform with relatively low autocorrelation sidelobe peak (ASP) and cross correlation peak (CP). In this paper, the signal model of MIMO radar is established firstly, and the basic principle of MIMO radar and the properties of transceiver channel matrix are analyzed.Because each waveform of OFDM signal can be separated, and linear frequency modulation signal (LFM) has a large time-bandwidth and wide-product, it can improve radar range and range resolution at the same time. Combining the characteristics of the two, this paper constructed ofdm-lfm signal model, and verified its theoretical orthogonality through the analysis of signal fuzzy function.Then the multiphase coded signal with good pulse compression performance is adopted to optimize the transmitted waveform by genetic algorithm at the cost of minimizing the peak side lobe.Finally, based on the sequential quadratic programming, the numerical relationship between the auto-correlation peak sidelobe level and cross-correlation peak level and the code length N, sequence number L and weighted coefficient is studied. KEY WORDSMIMO radar, ofdm-lfm signal, genetic algorithm, sequence quadratic programming

目录 1.1 1.2 第一章绪论.......................................................................................................................................1 MIMO 雷达波形设计的研究意义及背景......................................................................... 1 MIMO 雷达波形设计研究现状的国内外背景和历史发展.............................................1 第二章 MIMO 雷达概述......................................................................................................................3 2.1 MIMO 雷达的信号模型.................................................................................................. 3 一般信号模型.....................................................................................................................3 2.2 信号模型分类...................................................................................................................5 第三章正交波形设计.......................................................................................................................6 3.1 正交波形的基本概念和定义.......................................................................................... 6 3.2 正交波形设计的意义...................................................................................................... 7 OFDM-LFM 信号设计原理................................................................................................. 8 3.3 OFDM-LFM 信号模糊函数及波形....................................................................................... 9 3.4.1 遗传算法原理...................................................................................................... 12 3.4.2 使用普遍的几种代价函数和优化准则.............................................................. 12 第四章仿真结果及分析.................................................................................................................14 OFDM-LFM 波形设计与分析........................................................................................... 14 4.1 4.2 遗传算法仿真结果及分析............................................................................................ 21 4.3 序列二次规划算法........................................................................................................ 21 4.3.1 建立序列二次规划的数学模型........................................................................ 21 4.3.2 序列二次规划算法仿真结果及分析................................................................ 23 第五章总结与展望.........................................................................................................................27 致谢.................................................................................................................................................28 参考文献...........................................................................................................................................28 附录...................................................................................................................................................29

第一章绪论 1.1 MIMO 雷达波形设计的研究意义及背景以具有良好时间域中函数自相关的特点性能和时间域中互相关函数特点性能为波形设计的准则进行发射信号波形的优化。良好的时间域中自相关函数图像这一标准的达成可得到能够进行很好脉冲压缩的雷达信号的接收系统,使得目标的距离、速度和方位信息可以方便地提取。对于具有比较低的时域互相关特性的空间合成信号,可很大程度降低来自不同方向的目标返回波形之间的相互干扰。除此之外,整体的这个雷达系统在战场中得以生存下去的能力较高,而且敌方的侦察机也很难对其进行交叉确定其位置。 MIMO 雷达有两种,根据收发天线相互之间的距离,分布式的雷达为其中的一类,另一类是集中式雷达。较强的空间分集的本领是分布式这类 MIMO 雷达的特色, 可增强对闪烁(对于其散射截面积 RCS 的上升和伏动)目标的探测。传统意义上的单个发射站的雷达仅仅是一组发射信号波形,然而对于想要能在目标返回的信号波形上捕捉得到相互之间独立的信号的一些信息同时能够实现返回的波形之间的干扰的最大程度得减小,使得 MIMO 雷达发射的波形符合正交的标准。集中式 MIMO 雷达,属于传统的相控阵雷达的后代。相控阵这一类雷达中各个阵列单元能够产生出同样的波形,它一般是进行空间上信号波束的扫描,由不断改变各个阵列单元的移相器上的信号相位来实现,通常每个脉冲重复周期一次的移相周较长。上述可得相控阵雷达的发射信号波形比较单一,而且其波束在此停下的时长较大,因此敌方可以很容易得精准确定它的位置,从而敌人这一方的侦察机就可以发现它了,则其极大可能是被摧毁,所以在作战场地上生存下去的本领上处于劣势。然而集中式 MIMO 雷达有较高的信号波形的快速变化的本领,它的各个阵列单元都配有独立的快速产生信号波形的仪器。此外,集中式 MIMO 雷达处于相控阵这一类模式时是在对检测目标进行寻找的时期,按需分配发射电磁能量的情况属于目标跟踪阶段。由此可得出研究 MIMO 雷达的波形设计,在增强整个雷达系统的战争生存能力上,以及在对于现有传统意义上只有一个发射站的雷达和相控阵这类雷达发射的信号仅有一种的劣势克服方面具有重大意义,而且能够进行雷达信号发射的机器中能量的尽最大可能的利用,最终使得雷达接收信号波形的系统的检测信号波形的本领得以增强。 1.2MIMO 雷达波形设计研究现状的国内外背景和历史发展 2003 年,第一次给出了确切的 MIMO 雷达概念的是 MIT 林肯实验 Bliss D.W. 和 Forsythe K.W.等人,他们是在美国麻省理工学院,他们首先是将无线通信的 1

MIMO 技术运用到雷达系统中。并且指出了 MIMO 雷达是一种由产生多个不同种类的波形(就是运用波形分集的本领)来检索确定到其中一信道(也就是目标),同时通过相类似的多个方式接收处理信号的雷达系统。上述可以看出,自 MIMO 雷达的概念刚刚被提出开始,波形分集就成为了 MIMO 雷达的一个关键的议题,波形设计也就自然成为了其中重要的研究内容。 2004 年,正交波形的设计被 Deng Hai 首先对其展开了研究,他是美国德克萨斯大学的,信号的非周期自相关函数,以及信号波形的非周期互相关函数定义也通过他们被提出,对正交波形设计上的两种代价函数做出了说明,同时正交多相 ]2,0[  上相位是均匀离散取值)和正交频率编码的信号波形也是由他们通过模拟退火和邻域搜索的方法进行了设计 ,-14.8dB 的自相关峰值旁瓣电码(在平,-13.5dB 的峰值互相关电平是最终得出正交四相码性能的指标。这是由码长是 40,信号个数是 4 的波形得出的。在 2006 年,刘波和何子述等人在电子科技大学给出另一种设计方法,他们进行的是正交多相码和正交频率编码波形设计,结合了遗传算法和邻域搜索,这种优化速度以及其性能与 Deng Hai 的方法相比既快又好。另一方面正交线性调频(LFM)信号也被刘波等人进行了深入研究。对于遗传算法和模拟退火算法的收敛慢、局部收敛等一系列问题,西安科技大学的胡亮兵等人在基于序列的二次规划上,给出了相位连续的正交相位编码波形。随后是正交多相码具备了多普勒容限能力较强的性能,这是被 Hammad 和 David 等人在牛津大学运用互补 Frank 码设计出,同时也对信号的相位结构进行了充分分析而且通过用互熵理论得到的正交波形的多普勒容限好于 Deng Hai 的,然而总得来看, 对于多普勒敏感性问题的改善程度这种方法的作用仍然是有所局限的。可见设计正交均匀离散相位编码信号一般就是用到模拟退火、遗传算法和互 ]2,0[  相位上连续取值,1992 年,Kevin J.Gartz 的研究能够来详细讨论并解决这一问题,自相关旁瓣,以及随之而来的熵这些方法的。正交波形设计若是在互相关的四次方和是他所构造出的代价函数,恒定模值的信号波形相位的优化是 Fletcher-Reeves 进行的,他在该方法上的核心思想是共轭梯度法,自相关峰值旁瓣电平和峰值互相关电平很低且分布平坦的信号波形也是由他给出。,此外, 上述的这些新方法与 Kevin J. Gartz 的方法相比在性能指标方面比较差,如果说是具有相同信号码长,以及波形数目和码长的前提下,连续的相位取值就是其关键原因,而求解离散问题是比连续问题困难的。基于 FFT 的循环算法是通过相位连续取值的正交波形设计方法,是被 Li Jian 和 He Hao 于 2009 年在佛罗里达州大学再次提到的,该方法不仅采用了的代价函数是积分旁瓣能量,其具备计算占用的内存小等优点,而且得出了算法非常快速的实验结果,不过对比了 Kevin J. Gartz 的正交码,该方法的自相关峰值旁瓣电平,以及随之而来的峰值互相关电平是比较高的(关键是因为循环算法不能保证局部的收敛性,且以积分旁瓣能量 2

为代价函数)。本文第一步是对 MIMO 雷达的信号模型进行了建立,同时对 MIMO 雷达的接收和发送通道矩阵的性质,以及其基本的原理进行了分析。因为 OFDM 信号的每个波形能够分离,而且线性调频信号(LFM)具有大的时宽带宽积,雷达距离分辨力,以及其作用距离就能够与之同时得以提高,结合二者的特点。本文首先建立出 MIMO 雷达的信号模型，对 MIMO 雷达的基本原理和收发通道矩阵的性质进行了分析。因为 OFDM 信号的每个波形能够分离，而且线性调频信号（LFM）具有大的时宽带宽积，可以同时提高雷达作用距离和距离分辨力，结合二者的特点，本文构建了 OFDM-LFM 信号模型，并通过信号模糊函数的分析验证了其理论上的正交性。随后采用同样具有良好脉冲压缩性能的多相编码信号，以极小化峰值旁瓣为代价函数选择通过遗传算法对发射波形进行优化。最后，在建立的基于序列二次规划的数学模型上，通过对 Matlab 仿真实验结果的分析研究了自相关峰值旁瓣电平和互相关峰值电平与码长 N、序列数 L 和加权系数的数值关系，并对序列二次规划算法的优越性做出总结，更进一步在优化波形正交性未来研究方向上进行了展望。第二章 MIMO 雷达概述 2.1 MIMO 雷达的信号模型对于传统雷达,因为阵元间距特别小,同时假定目标位于远场,则把目标看作是点源目标。但事实上,雷达所有检测的目标由很多小的散射的个体组成,带有复杂的散射的背景,它的散射所带有的参数与方向位置角度呈现为函数关系。如果接收和发射之间的距离非常大,能够把目标看为是点目标就不能被视为可以理解的。随后便可以把目标视为是由大量的小散射的个体组成, MIMO 雷达发射信号波形模型的建立是通过了信号的传输流程(发射阵—目标—接收阵),进而对 MIMO 雷达的本质上的原理进行分析,考虑天线的分布阵列对目标的散射特征性能的影响大小。一般信号模型假定 MIMO 雷达为 M 个发射信号的天线,N 个接收信号的天线之间的距离是 td 和 rd ，目标是 Q 个小的散射个体的集合。为了使我们的描述和理解更加方便,则假定目标的 Q 个小散射体设置为均匀分布的线形的阵列,MIMO 雷达的接收和发射信号的天线阵列也都是均匀分布式的线性阵列,而且接收和发射信号的设备分开来放置(也能够接收和发射信号同时使用),和目标的信号阵列为平行的关系,如图所示。假定各个小的散射个体以同一方向性做出辐射,散射时的参数的实部和虚部都遵循的高斯分布,且其为零均值、方差为 1,则能够通过下面的对角矩阵对目标的散射的特征性能进行描述。  1 2 Q diag ([   Q , 1 , 0 ]) 1  （1） 3

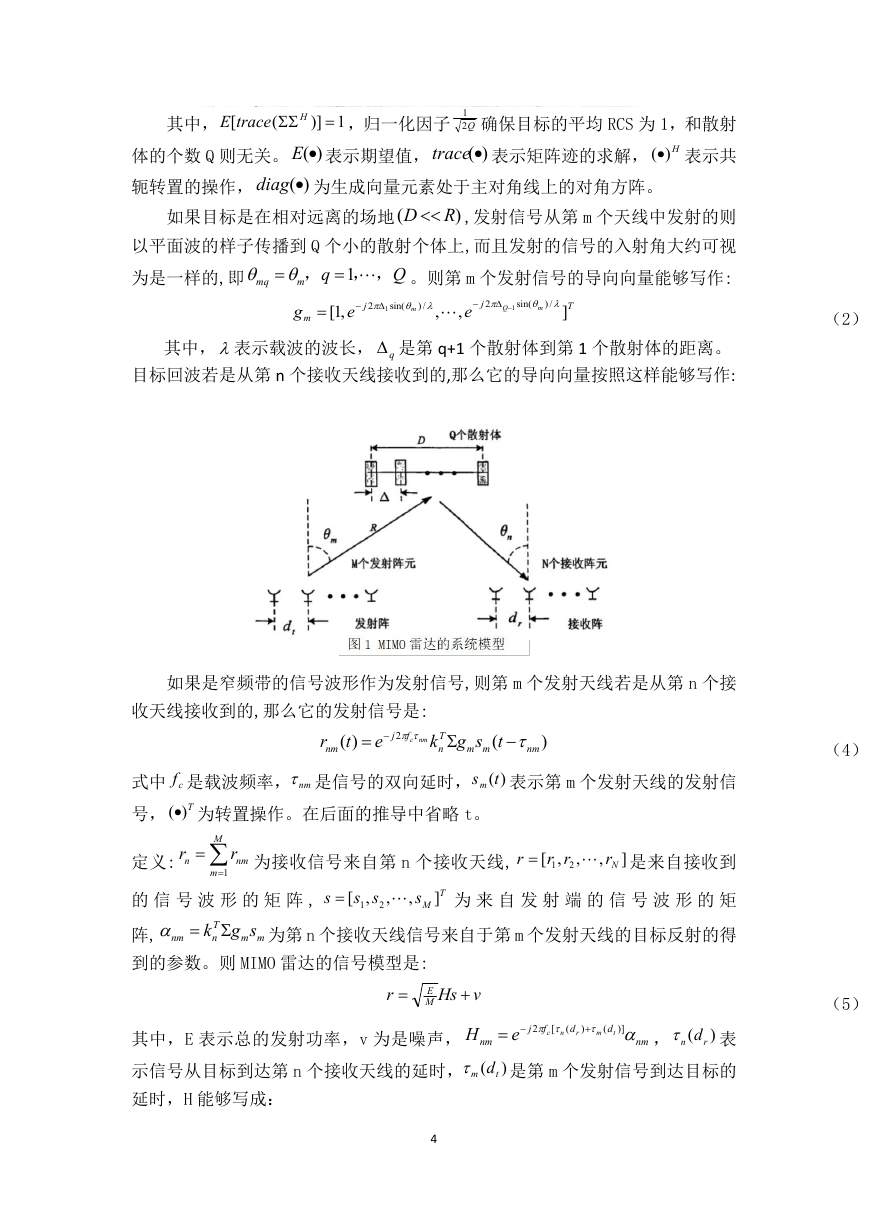
其中， E [ trace (  H 图 1 MIMO 雷达的系统模型 )] 1 ，归一化因子 Q2 1  体的个数 Q 则无关。 )(E 表示期望值，确保目标的平均 RCS 为 1，和散射 )( trace 表示矩阵迹的求解， H)( 表示共轭转置的操作， diag 为生成向量元素处于主对角线上的对角方阵。 )( 如果目标是在相对远离的场地 ( D  ) R ,发射信号从第 m 个天线中发射的则以平面波的样子传播到 Q 个小的散射个体上,而且发射的信号的入射角大约可视为是一样的,即  mq 。则第 m 个发射信号的导向向量能够写作: Q qm ，，， g  1 2 j   ,1[ e  1 m sin( m /)  ,  j 2   1 Q  , e sin( m /)  T ] 其中，表示载波的波长， q 是第 q+1 个散射体到第 1 个散射体的距离。目标回波若是从第 n 个接收天线接收到的,那么它的导向向量按照这样能够写作: 如果是窄频带的信号波形作为发射信号,则第 m 个发射天线若是从第 n 个接收天线接收到的,那么它的发射信号是: r nm )( t   e j 2 f  nmc k T n 式中 cf 是载波频率， nm 是信号的双向延时， )(t 号， T)( 为转置操作。在后面的推导中省略 t。定义:  为接收信号来自第 n 个接收天线, r nm r n  M m 1  ) ( t   nm sg  mm s m 表示第 m 个发射天线的发射信 r  ,[ rr 1 2 ,  , Nr ] 是来自接收到的信号波形的矩阵 , s  [ , ss 1  , 2 , Ms T ] 为来自发射端的信号波形的矩阵, k  nm T n sg mm 为第 n 个接收天线信号来自于第 m 个发射天线的目标反射的得到的参数。则 MIMO 雷达的信号模型是: r  E M vHs  其中，E 表示总的发射功率，v 为是噪声，示信号从目标到达第 n 个接收天线的延时， c j [ ( ) d 2 f  n H 表 m d 是第 m 个发射信号到达目标的   nm  e ) ( r n d nm ( t ， ) )] d m ( r t 延时，H 能够写成： 4 （2）（4）（5）

DH  M 11 21      12 1 M     22 2       2 N , , Mg 1 ,    ] 2 1 ， NM N ggG  [ B  DK T  GB       （6）， , ] Nk 2 j f  Nc  K 2 f  2 c ( [ d r , kk 1 2 ) ,  ,  , ) ,   , e  e j t )   j j 2 f  1 c ( d r   D B ) d   m ([ diag e  ([ e diag 为单位圆上的复数,影响不到 nm 的分布,所以能够把它 ( )] d 包含在 nm 中,则 nmH 和 nm 呈现出一样的分布。因此,信道矩阵 H 中每个信道参数都遵循的是高斯分布,是否相互之间独立则由接收和发射天线之间阵列单元之 , e  , e ]) ]) 由于 2 f  n je  2 f  Mc 2 f  2 2 f  1 d d d ( [ ) ( ( ) ( j j c c c r r t t ( d ) t 间的距离决定的。在下一小节中,按照 MIMO 雷达接收和发射天线阵列单元之间的距离的差异,对信道矩阵的性能特点进行分析,得到各类 MIMO 雷达的信号模型。 2.2 信号模型分类目标中大量散射的点得到一个阵列,其向后方向的散射信号的波束宽度为 2 / d ,如图所示。若波束所在地方 2R 的可达的域小于 ' 自于每个接收天线的目标各个部分的返回的波形都是有差异的,进而形成的接收 rd ,即为  时,来 R 2 / d ' dr 2 矩阵 K 的每一列之间都是不相关的,得到接收分集;若 ' dt  R 1 / d 1 ,按照同样的方法能够得到发射信号这方面的分集。所以,各反射参数之间是不是彼此独立取决图 2 阵元间距与目标反射系数的关系于阵列单元之间距离的大小。若接收和发射的阵列单元之间距离均特别大,能够得到接收和发射都能行的分集,则每个信道的反射系数相互之间是没有关系的各信道矩阵参数是遵循独立同分布的。那么,MIMO 雷达系统能够把它等同地视为是 MN 个单个的天线雷达同一时间均在工作。在统计这方面来分析,目标的返回的信号波形的 SNR 大约是一个不变的值,则可以消除掉来自于目标角的闪烁的后果,增强对于目标的检测和估计的本领。这一类雷达又被叫做统计 MIMO 雷达(statistical MIMO radar), 它的信号模型就是普遍的信号模型。第二种类型为传统意义上的相控阵模型,接收和发射的阵列单元之间距离均不能够很好达到分集的指标,每一个接收和发射天线从一样的角度探测到的目标, 就是 r 和 t （如果是仅有单个基地的雷达这类系统, r 和 r 为一样的），那么， MlgG  1 ， 2 sin( j    ,1[ g  1 ，其中， Ml 1 表示长度为 M 的全 1 向量， 2 2     1 1 Q Q N1 j   , e lkK ,  T ]  T ]  , ,1[ 2   1 sin( sin( sin(  e e e k , /) /) /) /)   j j r r t t   ，。 5

分享到：

赞收藏

资料库

MIMO雷达发射波形优化设计.pdf

相关推荐

课程资源

热门标签

最新资料