logo资料库

基于节假日GRNN-PSO的旅游客流量预测模型研究.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.30M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 基于节假日 GRNN-PSO 的旅游客流量预测 模型研究 # 赵凤华，陈立秀* （河北科技大学文法学院，石家庄 050000） 摘要：旅游客流量的预测是旅游景区科学应对旅游高峰的关键，尤其是在节假日。通过提出 GRNN-PSO 预测模型，针对 2011-2016 年四川九寨沟景区节假日客流量的变化进行系统的 实证研究。结果表明，与以往 SVR-PSO，BPNN，ARIMA 等预测方法相比，通过构建的 GRNN-PSO 预测模型具有较高的精度和良好的普遍性、实用性。采用 GRNN-PSO 预测模型 科学有效地预测旅游景区节假日客流量，可以准确掌握旅游景区在一定时期内旅游客流量的 变化，从而为旅游景区合理应对旅游节假日提供科学的理论指导。 关键词：旅游客流量；广义神经网络；粒子群；数据预测 中图分类号：F590.3 The Tourist Traffic Forecasting Based on GRNN - PSO Model ZHAO Fenghua, CHEN Lixiu (School of Humanity and Law, Hebei University of Science and Technology, Shijiazhuang 05000) Abstract: The forecast of tourist traffic is the key to deal with the peak of tourism, especially on holidays. In this paper, the GRNN-PSO model proposed, makes systematic and empirical study that aims at the change of he holiday traffic in Jiuzhaigou scenic area in Sichuan Province from 2011 to 2016. The study result shows that compared with the previous SVR-PSO, BPNN and ARIMA prediction methods, the study establishes GRNN-PSO forecasting model with higher accuracy and good adaptability. By adopting GRNN-PSO model that can scientifically and effectively forecast holiday traffic of tourist areas, we can accurately grasp the growth trend and speed of tourist area traffic for a certain period of time in future,which will provide a scientific theoretical guidance for the tourism scenic spot to deal with tourism holidays. Key words: Tourist traffic; GRNN; PSO; data forecasting 5 10 15 20 25 30 0 引言 35 40 当前，我国旅游产业发展势头强劲，并将成为拉动全球旅游产业发展的引擎。很多著 名旅游景区的游客数量常常处于饱和状态，甚至处于超负荷状态，尤其是在节假日期间。始 料未及的旅游高峰不仅对旅游景区、餐厅、宾馆的接待容纳能力是一个巨大的挑战，对景区 旅游资源的保护也是一种考验[1]。因此，越来越多的旅游景区开始重视节假日客流量的预测 工作，为即将到来的旅游高峰提前做好预防措施，但是由于我国的信息化发展比较缓慢，旅 游景区对以往客流量的记录很少，对客流量的预测大多基于管理经验和宏观预测，使客流量 的预测值与实际值之间存在很大的偏差[2]，因此需要建立一个能够真实准确反映旅游景区节 假日客流量的预测模型，为旅游景区积极应对旅游高峰提供一定的理论指导。 最初旅游景区客流量的预测是通过分析客流量的影响因子从而达到预测的目的，主要 采用计量经济学模型[3]，但是由于客流量的影响因子很难具体化，不仅耗时耗费大[4]，而且 预测结果容易受到人为因素的影响。除此之外，时间序列模型，BP神经网络等方法[5-7]也可 基金项目：河北省科技厅软科学课题（16450903D）；河北省硕/博创新基金资助项目（CXZZSS2017091) 作者简介：赵凤华（1960—），女，河北涿鹿县人，河北科技大学文法学院教授，研究生导师，主要研究 方向：中国传统文化. E-mail: zfh121@126.com - 1 -
    中国科技论文在线 http://www.paper.edu.cn 以达到预测的目的，但是由于缺乏前期对数据样本的学习过程，难以保证客流量预测结果的 准确性[8-9]。直到 20 世纪末，出现了支持向量机学习算法（support vector machine,SVM）[10-11]， 它夯实了统计学习理论基础，克服传统预测方法存在的缺点。把SVM应用到函数中，形成 支持向量回归（support vector regression, SVR）[12-13]。SVR模型善于解决小样本、非线性问 题，并成功应用于旅游景区客流量预测领域[14]。但是，SVR模型自由参数的选择容易影响实 际的预测结果，对于如何选择自由参数目前没有系统成熟的理论作指导。广义回归神经网络 （GRNN）是一种径向基神经网络的预测模型，该模型克服传统预测模型收敛速度慢、计算 工程浩大、初始化参数多等缺点，展现强大的非线性映射能力、容错性及鲁棒性[15]。GRNN 模型与RBF网络相比，在数据样本的基础上训练效果良好，学习和逼近能力强[16]。但是GRNN 各层参数的优化是非常困难的，寻找到最优的神经网络权重对预测结果非常重要。粒子群算 法（PSO）是基于种群进化算法的一种寻优方法，由于其容易实现且具有深刻的智能背景， 善于解决最优问题方面的鲁棒性和通用性，已经被广泛的应用于函数寻优等领域[17-19]。 文章提出了一种GRNN-PSO预测模型，把广义神经网络（GRNN）专门解决非线性问 题的优势与改进粒子群算法（PSO）的全局搜索能力的优势相结合，可以应用小样本数据进 行预测，实现对旅游景区节假日客流量的预测。为了实现GRNN参数的自适应选择，对PSO 模型进行改进，在原来的基础上提出动态双变异PSO预测模型，对GRNN的网络参数进行合 理的优化，避免局部最优和收敛速度慢的现象，获得全局的最优网络参数。本文提出 GRNN-PSO预测模型，针对 2011-2016 年四川九寨沟景区节假日客流量的变化进行系统的实 证研究。通过对比分析GRNN-PSO,SVR-PSO, BPNN, ARIMA等方法的的预测结果，阐述了 GRNN-PSO方法对旅游景区节假日客流量预测的有效性、普遍性。 45 50 55 60 1 GRNN-PSO 模型原理 1.1 GRNN 模型 GRNN 模型分四层，如图 1 所示，分别为输入层、模式层、求和层、输出层[20]。对应网 65 络输入 =X 1 xx ,,[ 2 T , nx ] 其输出为 =Y [ ， 1 yy , , 2 ny ] T 。 图 1 广义回归网络结构图 Fig. 1 Generalized regression network structure diagram 70 输入层神经元的数目与学习样本中输入向量的维数相同，每个神经元是简单的分布单 元，将输入变量直接传递给模式层。 模式层神经元数目与学习样本中的数目是相同的，每个神经元对应不同的样本。模式层 神经元传递函数为 - 2 -
    中国科技论文在线 http://www.paper.edu.cn ( p i = exp[ − XXXX i − − T () i 2 2 σ ) ] i = ,2,1 n （1） 神经元 i 的输出是输入变量与其对应的样本 X 之间的 Euclid 距离平方的指数平方 的指数形式。式中， iX 为第 i 个神经元对应的学习样本。σ为光滑因 XX ( − 子。 XX () T − ) i i 求和层主要用于对模式层中的神经元进行加权求和，传递公式为： S Nj n = ∑ i 1 = Py ij i , j = ,2,1 k （2） 式中，j 是输出层向量的维数。 输出层的神经元数和学习样本中输出向量的维数 k 是相同的，各神经元将求和层的输出 DS 相除，神经元 j 的输出对应估计结果 (ˆ XY 的第 j 个元素，即 ) jy = S S Nj D （3） 对于 GRNN 模型，是通过转换光滑因子σ，调整各个神经元之间传递的函数信息获取 最佳的回归估计结果，改变以往预测模型在训练过程中通过调整各个神经元之间连接权值获 取最优的预测结果。 1.2 PSO 模型及其改进 PSO 算法是一种基于种群全新的智能全局优化的进化算法。对于每一个粒子的速度按 照公式（4）进行更新，位置按照公式（5）进行更新[21]。 pr v v ( ϕω +⋅=+ i i 11 1 x x v = + ) x i gr ( + ϕ 22 − （4） best （5） x i best − ) i + 1 i i + 1 式中 iv 表示粒子第 i 次的速度；ω为惯性权重因子； 2 1,rr 1,ϕϕ 是粒子的加速度因子； 2 是(0,1)之间的随机数； ix 表示粒子第 i 次的位置； bestp 表示粒子个体最优值； bestg 表示群 体最优值。 许多学者对 PSO 基本模型都有深入的研究[22], 分析了基本模型中各个参数的作用和系 统的敛散性，同时提出了很多对基本模型中的参数进行改进的措施[23]。本文在综合分析这 些使得 PSO 具有更强的搜索能力和避免局部最优值。 1）许多文献已经证明[24]，惯性权重因子ω对 PSO 的性能具有直接决定性的影响，在本 模型的基础上，结合旅游景区客流量的实际问题，在基本 PSO 模型中加入了动态变化惯性 权重因子和双变异算子，文模型中我们引入了反正切函数下降策略，惯性权重不在是一个特 定的常数，新的惯性权重满足： t )( ωωω end − = init ( ) arctan t − T max T max （6） 式中， initω 是初始化惯性权重； endω 为最终惯性权重； maxT 为最大迭代次数；t 为当前 迭代次数。 2）在原来模型的基础上引入“变异”的思想，并对种群 内部各个粒子 以一定的概率 mP 按照种群最优和最劣的形式进行变异操作。在种群引入最差/最优变异算 xx 1 nx = x ) ( , , 2 - 3 - 75 80 85 90 95 100 105
    中国科技论文在线 子，变异后的粒子为 )5.01( γ+ ) 618 ζ = wor = best g g x x i j ⋅ st .01( +⋅ g 为种群最劣粒子； γζ, 服从 Gauss(0,1)分布的随机变量。 i xx , 为变异粒子； worst 式中， j 该法以大概率的初始化惰性粒子，以小概率的使最优粒子加强最优解附近的空间搜索。 （8） （7） http://www.paper.edu.cn 110 对于超出边界的粒子采取高斯白噪声变异。对超出范围的粒子 qx 进行如下变异 = x q x + min x 分别为粒子搜索空间在某个维度的上界和下界；σ是强度为 0dBW 的高 （9） ( σ min − ma x x ) max, x 式中 x 斯白噪声。 min 115 通过以上对基本 PSO 模型进行改进，形成了动态双变异 PSO 模型。使用该模型对 GRNN 120 125 130 135 140 σσ vx , 。 网络参数进行优化。其具体计算过程如下： 步骤 1 初始化粒子群的粒子为光滑因子σ，其初始位置和速度为 步骤 2 根据式（3）计算每个粒子的适应值，并且计算个体最优值、全局最优值和全局 最劣值。 步骤 3 根据式（6）更新权重因子，对适应值较差的粒子按照公式（7）进行高斯变异， 对陷入局部最优值的粒子按照公式（8）进行高斯变异。 步骤 4 判断是否有脱离搜索空间的粒子，如果有粒子脱离搜索空间，则按照公式（9） 进行高斯白噪声变异。否则，直接进入步骤 5。 步骤 5 按照式（4）、（5）进行粒子速度和位置的更新。 步骤 6 判断终止条件，如果符合终止条件，则输出最优；若不符合终止条件，这返回 步骤 2. 2 实验与分析 2.1 数据来源与模型建立 本文所使用的数据来源于四川九寨沟风景区官方网站统计，以 2011-2016 年九寨沟景区 节假日客流量的数据作为使用样本，如表 1 所示。将数据分成两部分进行训练和测试，即 2011-2015 年数据作为训练集，2016 年的数据作为测试集。 为了使用模型对节假日客流量进行预测，在 Matlab 2014a 软件上进行 GRNN-PSO 模型 的搭建。设置 GRNN 模型四层结构的参数数目，输入层的神经元设置 30 个参数，模式层和 求和层的神经元设置 30 个，输入层的神经元设置为 30 个，神经网络输入为 XXX，输出为 XXX，同时，神经网络验证方式采用 10 折交叉验证的方法。在改进的 PSO 算法中，种群规 模为 20，最大迭代次数为 1000，其他参数见表 2. 通过在仿真模型中反复验证，最终得到的 最优平滑因子σ为 2.3564. - 4 -
    中国科技论文在线 http://www.paper.edu.cn Tab. 1 Tab. 1 From 2011 to 2016, the tourist traffic of Sichuan Jiuzhaigou in the statutory holidays 表 1 2011-2016 年 四川九寨沟法定节假日客流量 2016 2015 2014 2013 2012 2011 清明节 (人次) 37427 35984 33596 27354 32578 25743 端午节 (人次) 47535 44844 41522 37747 31456 29537 劳动节 (人次) 50687 47818 44276 40251 35878 31979 中秋节 (人次) 55743 53251 49352 46215 42153 38613 国庆节 (人次) 209253 189155 177455 208416 250543 177454 145 注：数据来源:九寨沟景区官网 表 2 PSO 模型中其他参数 Tab. 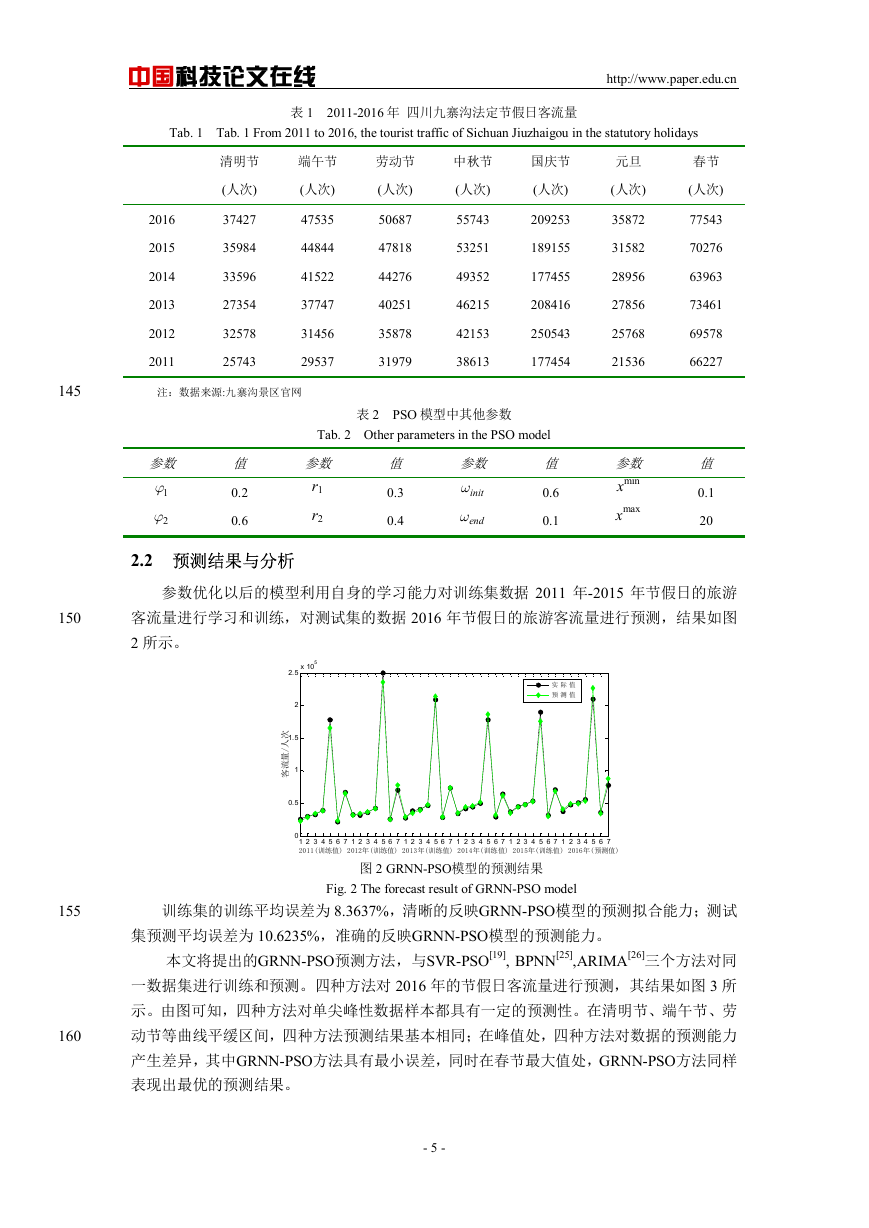2 Other parameters in the PSO model 参数 r1 r2 值 0.3 0.4 参数 initω endω 值 0.6 0.1 参数 1ϕ 2ϕ 值 0.2 0.6 2.2 预测结果与分析 元旦 (人次) 35872 31582 28956 27856 25768 21536 参数 xmin xmax 春节 (人次) 77543 70276 63963 73461 69578 66227 值 0.1 20 150 参数优化以后的模型利用自身的学习能力对训练集数据 2011 年-2015 年节假日的旅游 客流量进行学习和训练，对测试集的数据 2016 年节假日的旅游客流量进行预测，结果如图 2 所示。 x 105 2.5 2 实 际 值 预 测 值 1.5 1 次 人 / 量 流 客 0.5 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 2011(训练值) 2012年(训练值) 2013年(训练值) 2014年(训练值) 2015年(训练值) 2016年(预测值) 图 2 GRNN-PSO模型的预测结果 Fig. 2 The forecast result of GRNN-PSO model 155 训练集的训练平均误差为 8.3637%，清晰的反映GRNN-PSO模型的预测拟合能力；测试 集预测平均误差为 10.6235%，准确的反映GRNN-PSO模型的预测能力。 本文将提出的GRNN-PSO预测方法，与SVR-PSO[19], BPNN[25],ARIMA[26]三个方法对同 一数据集进行训练和预测。四种方法对 2016 年的节假日客流量进行预测，其结果如图 3 所 示。由图可知，四种方法对单尖峰性数据样本都具有一定的预测性。在清明节、端午节、劳 动节等曲线平缓区间，四种方法预测结果基本相同；在峰值处，四种方法对数据的预测能力 产生差异，其中GRNN-PSO方法具有最小误差，同时在春节最大值处，GRNN-PSO方法同样 表现出最优的预测结果。 160 - 5 -
    中国科技论文在线 http://www.paper.edu.cn x 105 3 / 次 人 量 流 客 2.5 2 1.5 1 0.5 实际值 GRNN-PSO SVR-PSO BPNN ARIMA 0 清明节 端午节 劳动节 中秋节 国庆节 元旦 春节 图 3 2016 年不同方法的预测结果 Fig. 3 The forecasting results of different methods in 2016 year 表 3 详细列出了四种方法对 2011-2016 年客流量训练结果、预测结果的最大误差、最 小误差、平均误差。通过表 3 可以看出GRNN-PSO模型对数据的预测能力在误差最大值、误 差最小值和误差平均值均具有优势。GRNN-PSO模型与SVR-PSO和ARIMA模型相比， SVR-PSO和ARIMA模型的训练误差和预测误差高 1%-3%左右，但是GRNN-PSO模型需要优 化的参数要远远小于其他两种方法，算法收敛更快。与BPNN网络相比，GRNN-PSO模型具 有绝对的优势。 表 3 四种方法结果误差比较 Tab. 3 Comparison of Four Methods Result Errors 最大值 训练集 最小值 平均值 最大值 预测集 最小值 平均值 GRNN-PSO 16.3284% 1.2653% 8.3637% 17.3584% 5.2357% 10.6235% SVR-PSO 24.3256% 2.3279% 9.0356% 27.9968% 5.9532% 12.8235% BPNN 22.3254% 5.3265% 13.5274% 24.3698% 8.3652% 16.3547% ARIMA 19.3658% 2.0214% 9.3657% 18.2365% 5.9982% 13.2675% 3 结论 本文提出的 GRNN-PSO 预测模型，把广义回归神经网络专门解决非线性问题的优势与 改进的粒子群优化算法的全局搜索能力相结合，可以准确的实现对旅游景区节假日客流量的 预测，即使应用小样本数据，也能达到良好的预测效果。 （1）GRNN 模型，在以往数据的训练和学习过程，综合考虑天气、交通、门票价格等 多种影响因素，增强对旅游景区节假日客流量变化趋势的掌握，使预测数据更合理可靠。 （2）本文对 PSO 模型进行改进，在原来的基础上提出动态双变异 PSO 预测模型，对 GRNN 的网络参数进行合理的优化，避免局部最优和收敛速度慢的现象，获得全局的最优 网络参数，增强预测结果的精准度。 （3）与以往 SVR-PSO, BPNN, ARIMA 等预测方法相比，对四川九寨沟景区节假日客 流量的实证研究，GRNN-PSO 预测模型均充分显示出较高的精准度以及良好的普遍性、实 用性。GRNN-PSO 预测模型，为旅游景区科学有效地预测节假日客流量，准确掌握节假日 旅游客流量的变化提供科学合理的理论指导。 - 6 - 165 170 175 180 185
    中国科技论文在线 http://www.paper.edu.cn 但是，GRNN-PSO 预测模型也存在一定劣势，在预测过程中受多种因素的影响，如旅 游客流量的数据统计源于官网相关报告和网络，信息不能全面的覆盖。同时，与节假日客流 量在模型的深入研究、模型参数的选取上还有待完善。 190 [参考文献] (References) 195 200 205 210 215 220 225 230 [1] 翁钢民,李凌雁,李慧盈.季节调整的 PSO-SVR 模型及其在旅游客流量预测中的应用--以海南省三亚市 为例[J].数学的实践与认识, 2016, 46(6):6-13. [2] 任 乐,崔东佳.基于网络搜索数据的国内旅游客流量预测研究--以北京市国内旅游客流量为例[J].经济问 题探索, 2014(04): 67-73. [3] Smeral E, Witt S F,Witt C A.Econometic forecasts: Tourism trends to 2000[J]. Annals of Turism Research, 1992, 19(3):456-466. [4] 李志龙, 陈志钢,覃智勇.基于支持向量机旅游需求预测[J].经济地理,2010, 30(12):2122-2126. [5] 杨名桂,杨晓霞.基于灰色预测模型的重庆市入境旅游客流量预测[J].西南师范大学学报:自然科学 版,2010,35(3):259-26. [6] 朱晓华,杨秀春.旅游客源预测模型及其对比[J].地理与地理信息科学,2004,20(5):84-87. [7] 雷可为,陈 瑛.基于 BP 神经网络和 ARIMA 组合模型的中国入境游客量预测[J].旅游学刊,2007,22(4): 20-25.] [8] Cao X P,Yi D Y,Wu Y,et al.The development of time series forecasting based on neural network[J]. Computer and Information Technology, 1999(6):1-3. [9] Law R,Back-propagation learning in improving the accuracy of neural network- based tourism demand forecasting[J]. Tourism Management, 2000, 21(4): 331-340. [10] Vapnik V N.The nature of statistical learning theory[M]．许建华,张学工,译.北京：电子工业出版社,2009. [11] 肖 智,李玲玲.PSO-SVM 在高速公路交通量预测中的应用[J].管理评论, 2011, 23(12):32-37. [12] 王瑞雪,刘 渊. GAFSA 优化 SVR 的网络流量预测模型研究[J].计算机应用研究, 2013,30(3): 856-860. [13] 夏国恩,邵培基.改进 SVR 在金融时间序列预测中的应用[J].金融理论与实践,2008,(3):95-98. [14] Chen K Y. Combining linear and nonlinear model in forecasting tourism dsmand[J]. Expert Systems with Applications, 2011,38(8):10368-10376. [15] 孔国利,张璐璐.遗传算法的广义回归神经网络建模方法[J].计算机工程与设计,2017,38(2):487-493. [16] 张强劲,陈忠华.基于 GRNN 算法的潜在产出与产出缺口估算模型[J].重庆大学学报,2016,39(6):148-154. [17] 陈传亮,田英杰,别荣芳．基于粒子群优化的 SVR 算法与 BP 网络的比较研究[J].北京师范大学学报:自然 科学版,2008, 44(5): 449-453. [18] Liu Li-xia, Zhuang Yi-qi, Xue-yong Liu. Tax forecasting theory and model based on SVM optimized by PSO Original Research Article[J].Expert Systems with Applications, 2011, 1(38): 116-120. [19] 陈 荣,梁昌勇,陆文星等.基于季节基于季节 SVR_PSO 的旅游客流量预测模型研究[J].系统工理论与实 践, 2014, 35(5): 1290-1296. [20] John Y. Goulermas, Xiao-Jun Zeng, Panos Liatsis, Jason F. Ralph. Generalized Regression Neural Networks With Multiple-Bandwidth Sharing and Hybrid Optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2007, 37(6): 1434-1445. [21] FU Yang-guang, ZHOU Cheng-ping, DING Ming-yue.3-D Route Planning Based on Hybrid Quantum-Behaved Particle Swarm Optimization[J]. Journal ofAstronautics, 2016, 31(12): 2657-2664. [22] Y. Sun, L. Zhang, X. Gu, A hybrid co-evolutionary cultural algorithm based on particle swarm optimization for solving global optimization problems[J]. Neurocomputing, 2012, (98) 76-89. [23] Coorenm, M. Clerc, P. Siarry, MO- TRIBES:an adaptive multiobjective particle swarm optimization algorithm[J]. Comput. Optim. Appl., 2011, 49(2): 379- 400. [24] P. K. Tripathi, S. Bandyopadhyay, S.K. Pal, Multi-objective particle swarm optimization with time variant inertia and acceleration coefficients[J]. Inf. Sci. ,2007,177 (22) :5033-5049. [25] 石 黎, 史玉珍.城市水资源 可持续利用评价的 改进 BPNN 模 型--以湖 北省为例[J]. 科 技管理研 究,2014,(12):46-49. [26] 肖 良.基于季节性 ARIMA 模型的居民消费水平预测[J].统计与决策, 2016, (8):83-86. - 7 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料