logo资料库

结合置乱变换和DCT变换的图像水印分析.doc

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.34M 资料格式：doc 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    基于置乱变换的 DCT 域水印分析 摘 要 提出一种符合 Kerckhoff 原则的 DCT 域数字水印算法． 该算法在嵌入 水印前对水印进行 Arnold 变化，并通过密钥向量嵌入水印图像，大大提高了水 印的鲁棒性和安全性． 对比实验表明，该方案对高斯低通滤波、添加白噪声、 JPEG 压缩、图像剪切等攻击手段有较好的鲁棒性，并具有较高的安全性． 关键词 Arnold 变换，离散余弦变换，Kerckhoff 原则，数字水印 随着互联网和通信技术的不断发展，数字产品越来越多地被广泛使用． 数 字产品的大量使用为信息的存取提供了极大的便捷，但由于数字产品容易被拷贝 和传播，数字产品的信息安全、版权保护已成为重要的社会问题和技术议题 1-3］． 在这种情况下，数字水印技术应运而生，并引起人们的高度重视，成为 多媒体信号处理领域的一个研究热点［4-5］． 起初学界对数字水印的研究基本 上是基于时空域的，时空域算法相对简单，但是其鲁棒性等性能相对较差． 自 从 1996 年出现了第一个变换域算法，变换域算法以其优秀的特性而受到广泛关 注，很多研究者开始研究不同变换域的水印算法，包括离散余弦变换( DCT) 、 离散傅立叶变换( DFT ) 和离散小波变换( DWT ) 等． 近年来，数字水印的研究 主要集中在改善数字水印理论，提高数字水印算法的鲁棒性和安全性，并研究其 在网络中的实际应［6-7］． 文献［8］中提出一种基于 Arnold 变换的 DCT 域图像水印算法． 该方 案切实可行，具有一定的安全性与鲁棒性． 但该方案的安全性依赖于对算法的 保密，不符合 Kerckhoff 原则; 通过实验表明，该方案抵抗高斯低通滤波、添加 白噪声等攻击手段能力相对较弱． 本文提出的基于 Arnold 变换的 DCT 域数 字水印改进算法，在数字水印的安全性和鲁棒性 2 方面有明显的提高． 1 置乱与 Arnold 变换 所谓“置乱”，是指利用数字图像具有的数字矩阵的特点，通过一些变换或 数学上的特殊性质，搅乱图像中像素的位置，将原来有意义的图像信息变换成一 幅“杂乱无章”的图像，使得无法辨认出原始图像信息，从而达到在一定程度上 迷惑第三者的目的［9］． 作为常见的置乱变换之一，Arnold 变换广泛地被用于数字水印技术中，它 是 Arnold 在研究遍历理论过程中提出的一种像素位置变换［10］Arnold 的变 换规则［11］为 Arnold 变换具有周期性，即当迭代到特定的步数时，将得到变换前的原始图像 ［12］． 对于二维 Arnold 变换来说，不同阶数的图像矩阵存在不同的变换周期， 具体如表 1 所示．
    2 离散余弦变换( DCT) 离散余弦变换( discrete cosine transform，简称 DCT 变换) 是 Ahmed N 等人 在 1974 年提出的正交变换方法，被认为是对语音和图像信号进行变换的最佳方 法［13］． 它是一种与傅立叶变换紧密相关的数学运算． 在傅立叶级数展开式 中，如果被展开的函数是实偶函数，那么其傅立叶级数中只包含余弦项，再将其 离散化可导出余弦变换，因此称之为离散余弦变换． 设 A 为 M* N 的图像矩阵，则该图像的二维 DCT 变换可由式( 2) 表示: 矩阵 B 是图像 I 经过二维 DCT 变换得到的 DCT 系数矩阵，其中低频分 量将集中在矩阵的左上角，高频分量则集中在右下角［14］． 在数字图像中，低 频部分代表整体部分，若在低频部分嵌入水印信息则不易丢失，但容易被人察觉; 高频部分代表整体部分，若在高频部分嵌入水印信息则容易丢失． 因此，本文 的方案是在中频部分嵌入水印信息． 3 算法思想 3. 1 算法思路 本文提出一种基于 DCT 变换且符合 Kerckhoff 原则的数字水印算法．根 据 Kerckhoff 原则，所有算法都是公开的，只有密钥是保密的． 密码算法必须 经过公开的研究和攻击，其安全性才能得到认可． 水印算法也一样，应当公开， 其安全性应当仅依赖于对于密钥的保密． 算法的公开曾经使密码学得到巨大的 发展． 在数字水印领域中，公开算法也正在成为新的趋势［15］． 根据笔者设计的算法，首先对水印图像进行 Arnold 变换，然后对载体图进 行离散余弦变换． 在正式嵌入水印信息时，生成服从正态分布的一维伪随机向 量 V 1、V2 作为密钥，选取经过 DCT 变换后载体图像中的中频位置嵌入水印 信息，最终得到含有水印的图像． 这样将很大程度上提高水印的安全性和鲁棒
    性． 3. 2 水印嵌入步骤 周期 T 和置乱次数 K; 1) 对水印图像 M 进行 Arnold 置乱变换，得到 M'，保留水印图像的 Arnold 2) 将载体图像分割为互不重叠的图像块 Block( x，y) ，分割的图像块数等 于水印图像的像素数，并对分割后的各图像块进行 DCT 变换; 3) 生成 2 个长为 L 的一维向量 V1、V2，其中，V1、V2 为服从均值为 0、 方差为 1 的正态分布的伪随机向量，L 为每一个图像块中嵌入信息的像素数; 4) 读取二值水印图像中的一个元素 M'( p，q) ，根据式( 3) 为向量 V 赋值: 其中，0 ≤ p ≤ M － 1，0 ≤ q ≤ N － 1． 然后根据式( 4) ，在对应图像块 DCT 域的 L 个中频系数位置嵌入水印信息: 其中，1 ≤ t ≤ L，Block ( it，jt) 为嵌入点位置，α 为尺度因子． 5) 对嵌入水印信息后的图像块进行 IDCT 变换，并将所得图像进行合并， 得到含水印的载体图像; 6) 公开嵌入点位置． 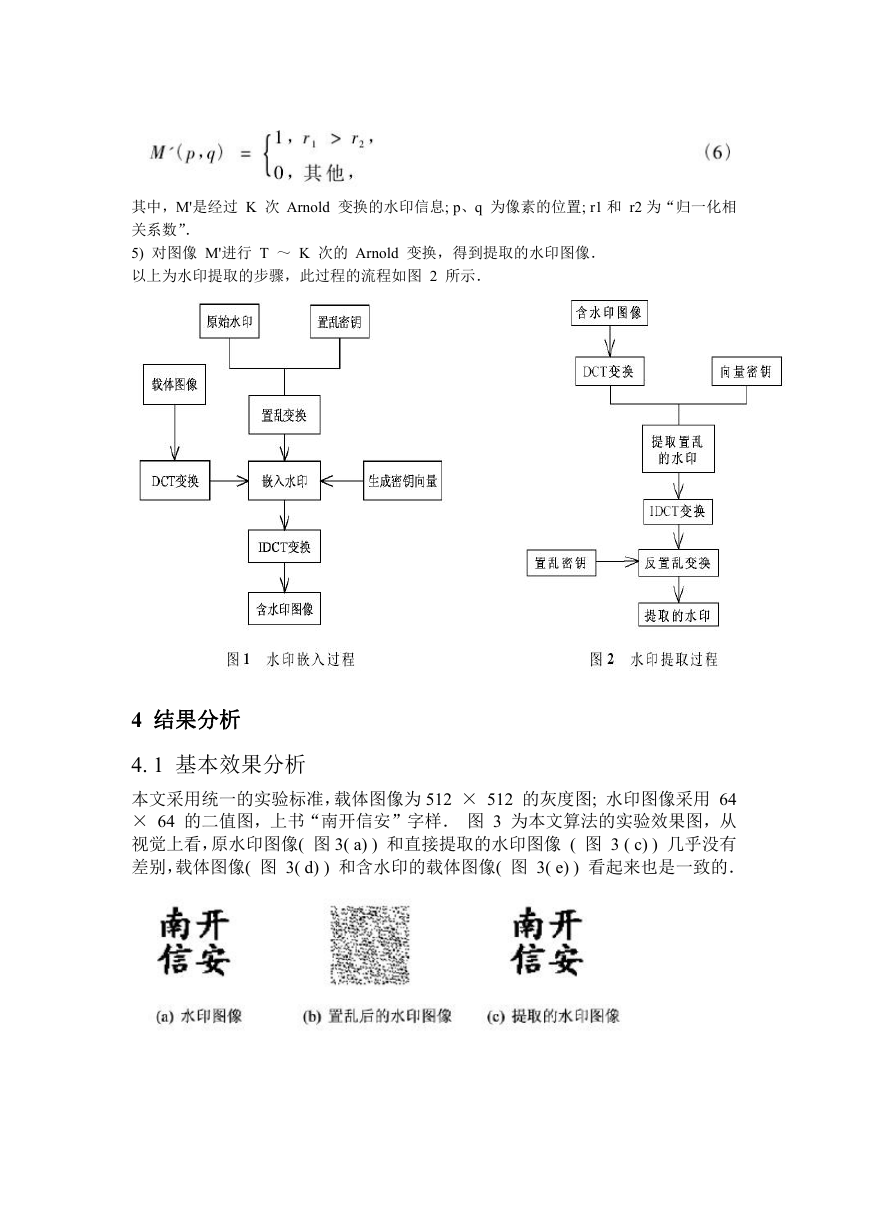以上为水印嵌入的步骤，此过程的流程图如图 1 所示． 3. 3 水印提取步骤 1) 通过可信信道，获取密钥( V1、V2、K、T) ; 2) 将含有水印的载体图像分割为互不重叠的图像块，分割的图像块数等于水印 图像的像素数，并对分割后的各图像块进行 DCT 变换; 3) 定义一个长为 L 的一维向量 V'，对于每一个像素块，将 L 个嵌入点的值赋 给向量 V'． 然后根据公式( 5) ，分别计算出 R( V1，V') 和 R( V2，V') ，结 果分别记为 r1 和 r2，其中，R( V1，V') 为 V1 与 V'的归一化相关系数，R( V2， V') 为 V2 与 V'的归一化相关系数. 其中，A、B 为 2 个 m* n 的矩阵，A、B 分别为矩阵 A、B 的平均值． 4) 根据式( 6) ，判断置乱变换后水印中每个像素的值．
    其中，M'是经过 K 次 Arnold 变换的水印信息; p、q 为像素的位置; r1 和 r2 为“归一化相 关系数”． 5) 对图像 M'进行 T ～ K 次的 Arnold 变换，得到提取的水印图像． 以上为水印提取的步骤，此过程的流程如图 2 所示． 4 结果分析 4. 1 基本效果分析 本文采用统一的实验标准，载体图像为 512 × 512 的灰度图; 水印图像采用 64 × 64 的二值图，上书“南开信安”字样． 图 3 为本文算法的实验效果图，从 视觉上看，原水印图像( 图 3( a) ) 和直接提取的水印图像 ( 图 3 ( c) ) 几乎没有 差别，载体图像( 图 3( d) ) 和含水印的载体图像( 图 3( e) ) 看起来也是一致的．
    4. 2 鲁棒性实验与分析 为检验本文方案的鲁棒性，笔者对含水印的载体图像分别进行高斯低通滤波、添加白噪声、 JPEG 压缩以及剪切等攻击，记录不同攻击方式下含水印的载体图像和从中提取的水印图 像，如图 4 所示． 另外，记录本方案在未受攻击和不同攻击情况下的峰值信噪比( PSNR) 和 归一化相关系数( NC) ，如表 2 所示． 其中 PSNR 为原载体图像和含水印的载体图像之 间的峰值信噪比，用以表示载体图像在嵌入水印后的变化情况; NC 为原始水印图像和提取 的水印图像之间的归一化相关系数，用以表示提取水印图像的质量［16］. 根据图 4 所示，可以看到在不同情况下提取的数字水印图像比较清晰． 根据表 2 所示， 实验中 PSNR 都在 30dB 以上，相对较高，说明嵌入水印并未对载体图像造成过大影响; NC 在未攻击的情况下为 1，在 JPEG 压缩的情况下为 0. 9984，在受到其他攻击的情况下 也都保持在 0. 97 以上，可见本方案对 JPEG 压缩有很好的鲁棒性，对高斯低通滤波、添加 白噪声和剪切也有较好的抵抗效果． 为了进一步验证本方案的鲁棒性，笔者将本文提出的改进方案和文献［5］中的原方案
    做了攻击实验对比． 为区分 2 种方案，这里将本文提出的方案称为“方案 A”，将文献［5］ 中的原方案称为“方案 B”．由于篇幅有限，这里只对高斯低通滤波和添加白噪声 2 种情 况进行对比，如图 5 所示． 可见，方案 B 受到高斯低通滤波攻击后，提取的水印已经出 现比较严重的失真; 在受到白噪声攻击后提取的水印已经无法辨识，失去了效果． 通过对 比可以看出，本文提出的方案与原方案相比，有较大的改善，鲁棒性较强． 5 结束语 本文提出一种基于 Arnold 变换的 DCT 域数字水印改进算法． 本算法在 嵌入水印前对水印图像进行 Arnold 变换，并引入密钥向量来进行水印的嵌入， 使得本算法的安全性仅依赖于对密钥的保密，符合 Kerckhoff 原则，很大程度上 提高了本方案的安全性． 同时，通过与文献［8］中的原方案进行攻击实验对比， 可以看出，本方案对于 JPEG 压缩、高斯低通滤波、添加白噪声、剪切处理都 具有较好的鲁棒性． 进一步的工作包括选择更加有效的水印嵌入点，使本方案在保持较高鲁棒 性的基础上，进一步提高嵌入水印后载体图像的质量． 参考文献 ［1］ An S F，Wang C Y． A computation structure for 2-D DCT watermarking［J］． Circuits and Systems，2009: 577-580． ［2］ Cox I J，Ikkern N L，Bloom J A． Digital watermarking［M］． 王颖，译． 北京: 电 子工业出版社，2003: 127． ［3］ Li X D． Geometric attack resistant image watermarking in spatial domain［J］． Acta Automatica Sinica，2008，34( 7) : 832-837． ［4］ Zhang X H，Wei P C． Study of digital watermarking based on information theory ［J］． Computer Science，2009，36( 3) : 248-255． ［5］ Nguyen T V，Patra J C． A simple ICA-based digital image watermarking scheme ［J］． Digital Signal Processing，2008 ( 5) : 762-776． ［6］ Xiao J，Wang Y． A robust digital watermarking algorithm based on multiple-level discrete cosine transform［J］． The Chinese Journal of Computers，2009，32( 5) : 1055-1061( in Chinese) ． 肖俊，王颖． 基于多级离散余弦变换的鲁棒数字水印算法［J］． 计算机学报，2009，32( 5) :
    1055-1061． ［7］Huang J W，Shi Y Q．Embedding image watermarking in DC component［J］．IEEE Trans on Circuits and Systems for Video Technology， 2000，10( 6) : 974-979． ［8］ He W． Research and implementation of image watermarking technology based on transformation domain［D］． Changchun: Jilin University， 2008． ［9］ Zhang C J，Wang J S，Wang X D． Digital image watermarking algorithm with double encryption by arnold transform and logistic［J］． Networked Computing and Advanced Information Management，2008: 329-334． ［10］ Feng M Y，Feng B，Shen C L． Adaptive image watermarking algorithm based on block DCT transform and arnold shuffling［J］． Computer Applications，2008，28( 1) : 171-173． ［11］ Zhang J，Yu X Y，Reng H E． Improved image scrambling algorithm of arnold cat transformation［J］． Computer Engineering and Applications，2009，45( 35) : 14-17． ［12］ Wang J H． Improved particle swarm algorithm based on arnold map［J］． Computer Science，2010，37( 6) : 268-270． ［13］ Navas K A，Ajay M C，Lekshmi M ，et al． DWT-DCT-SVD based watermarking［C］ ∥3rd International Conf on Communication Systems Software and Middleware and Workshops( COMS WARE 2008) ． 2008: 271-274． ［14］ Pan G，Wu Z H，Lü H B，et al． A bi-image watermarking method based on 2D-DC ［J］． Journal of Engineering Graphics，2000 ( 3) : 118-125( in Chinese) ． 潘纲，吴朝晖，吕红兵，等． 基于二维 DCT 的双图像数字水印算法［J］． 工程图学学报， 2000 ( 3) : 118-125． ［15］ Furon T，Duhamel P． An asymmetric watermarking method［J］． IEEE Transactions on Signal Processing，2003，51( 4) : 981-995． ［16］Guo F X，Wang X，Chen W W．Digital watermark algorithm resisting to geometric attack based on histogram specification［J］． Computer Engineering，2009，35( 16) : 130-132．
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料