logo资料库

相干多普勒测风激光雷达时域信号仿真及时频分析.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：4.15M 资料格式：pdf 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    第 42 卷 第 1 期 2015 年 1 月 中 国 激 光 CHINESE JOURNAL OF LASERS Vol. 42, No. 1 January, 2015 相干多普勒测风激光雷达时域信号仿真及时频分析 白 雪 郭 磐 陈思颖 张寅超 陈 和 步志超 北京理工大学光电成像技术与系统教育部重点实验室, 北京 100081 - (feuilleté model) (NASA) 阵风模型下仿真回波信号。对仿真信号作 进行非平稳信号的仿真。引入时 Wigner-Ville 摘要 基于大气分层时域信号生成模型 频域联合分析方法反演风 速，对非平稳风速模型下的仿真回波信号进行算法处理研究。基于实际系统参数，分别在线性剪切风速和美国宇 航局 变换，通过分析信号时频变换后的能量峰值在 时频面内的分布来反演风速。采用多组脉冲累加平均的方式来减少因散斑噪声、交叉项等因素造成的反演风速的 波动。结果表明，利用时 频域联合分析方法可以快速反演出风速信息，无需对探测范围进行距离门的划分；对多 组信号的时频变换结果做累加平均处理后，反演风速的波动减小，与输入风速的一致性得到了明显的改善。 关键词 遥感 中图分类号 ; TN247 相干多普勒测风激光雷达 时域信号仿真 文献标识码 风速反演 时频分析 - ; ; A ; doi: 10.3788/CJL201542.0114003 Simulation in the Time Domain and Time-Frequency Analysis for Coherent Doppler Wind Lidar Bai Xue Guo Pan Chen Siying Zhang Yinchao Chen He Bu Zhichao Key Laboratory of Photoelectronic Imaging Technology and System, Ministry of Education, Beijing Institute of Technology, Beijing 100081, China Abstract An atmospheric slices time domain signal generation algorithm model (feuilleté model) is proposed to simulate the signal under non- stationary atmospheric conditions. The wind inversion by means of time- frequency analysis is introduced, and the algorithm processing of signals simulated under non-stationary wind model is studied. Based on the actual system parameters, the echo signals are simulated under conditions of linear wind shear and national aeronautic and space administration (NASA) typical wind shear model, respectively. Wind inversion by analyzing the distribution of peak energy in the time- frequency domain after the application of Wigner- Ville transformation on the simulated signal is got. And in this process, the fluctuation of wind inversion, which results from speckle noise, cross terms and other factors, can be reduced by accumulating multiple time- frequency transforms of pulses. The results show that, wind inversion is obtained quickly and directly by utilizing time-frequency analysis methods and without division of range gate in detection zone. The fluctuation of wind inversion decreases after the processing of accumulation and average, and the similarity between wind inversion and input wind speed is improved significantly. Key words domain signal simulation OCIS codes 010.3640; 280.3640; 010.0280; 070.1170; 280.3340 remote sensing; coherent Doppler wind lidar; wind inversion; time- frequency analysis; time 收稿日期: 2014-07-01; 收到修改稿日期: 2014-08-26 基金项目 (61178072) : : : (1990—) (1981—) 作者简介 E-mail: guopan@bit.edu.cn( 导师简介 国家自然科学基金 白 雪 郭 磐 ，女，硕士研究生，主要从事激光雷达大气风场测量方面的研究。 ，男，博士，讲师，主要从事激光雷达信号获取与处理算法方面的研究。 通信联系人 ) E-mail: baixue621@126.com 0114003- 1
    1 中 国 激 光 引 言 大气风场的精确测量对气象系统动力学模型研究、数值天气预报的改进、军事环境的精确性预报等都有 。目前 重大意义，可用于监测机场风切变、监视飞行路线前方的风场情况，为航空航天提供重要的安全保障 已有多种大气风场的测量方法，如无线电探空系统、微波雷达等 。多普勒测风激光雷达，相对于微波雷达来 说波长较短，大气的后向散射较强，适合用于晴空探测，美国、日本和欧洲各国都对其都投入了大量的研究。 ，系统复杂、设备要求高、成本昂贵，利用计算机仿真是一种 可行的研究方法。本文基于大气分层模型 ，考虑激光束的传播及其与大气的相互作用，探 测体内的风速细节，结合实际的系统参数，对相干多普勒测风激光雷达在非平稳大气情况下的回波信号进 行时域仿真，得到时变信号用于后续的数据处理与验证。 相干测风激光雷达系统采用相干接收体制 (feuilleté model)[4] [3] [2] [1] - 、克 拉 默 和最大似然算法 (FFT)[5] 利用数据处理算法对仿真的回波信号进行验证、分析和风速反演。目前应用于相干测风激光雷达的数 、多 脉 冲 对 算 法 等。其中快速傅里叶变换是数据处理中最常用的算法。它对每个距 频域联合分析方法可以直 (NASA) 频率密度函数形式表示出来，快速得到不 变换对仿真回波信号进行了风速反演的 (poly-pulse pair) (ML)[8] 据 处 理 算 法 主 要 有 ：快 速 傅 里 叶 变 换 - 离门内的信号序列作傅里叶变换及功率谱估计。与快速傅里叶方法相比较，时 接对多个距离门进行连续处理，将一维的时间信号以二维的时间 Wigner-Ville 同探测距离处的频谱数值进而反演出风速值。本文分别在理想的线性剪切风速模型和美国宇航局 阵风模型下，进行回波信号的仿真及可靠性验证；基于 分析和验证。 (CRLB)[6] 拉 奥 下 界 算 法 、脉 冲 对 算 法 - [7] 2 2.1 大气分层模型 目标回波的时域模型及时变特性分析 [9] 相干多普勒测风激光雷达基于光外差探测原理 107 ，通过接收大气中气溶胶粒子的后向散射光，以获得足 ，数量可达 数量级。因此回波信号的强度和相位都存在很强的随机性，由单个粒子的散射计算回波信号是非常 够强的多普勒测风信息。每一时刻激光束作用体积内的气溶胶粒子尺度分布极广，随机性很强 到 困难的。 [10] 基于端到端的大气分层模型对非稳定大气条件下的相干多普勒测风激光雷达的回波信号进行时域仿 R ，并假设每一 。通过全部分层回波信号的叠加得 真。大气分层模型将探测范围内的气溶胶散射体沿光束传播轴分为 M 层，每一层的厚度为 107 层内的气溶胶粒子运动速度大小和方向相同、散射系数恒定 到总的回波信号。层数 M 的取值一般为几百到上千，与 ( 相比大大减小了计算量。 如图 所示 1 ) Δ 1 Fig.1 Schematic of atmospheric slices time domain signal generation algorithm model = T 为采样时间。层数 M Δ T ，其中 c 为光速， 大气分层模型原理示意图 = 1/2 × × Δ Δ 图 R c 所示，分层厚度 1 如图 × c /(2Δ ) R PT ，PT 是 发射激光脉冲宽度。 假设层与层之间的回波信号相互独立，将每一层的回波信号进行非相干累加，可得到总的回波信号为 S( )t ，其可表示为 0114003- 2
    = 2( 1 2 exp( i2π S( )t )PLO R c )W 是本振光功率，PT 是发射的激光脉冲，υIF 是声光频移量，R φæ ç è υIF t ) t m m K ù ö ú ÷ ø û 是每层中心与接收平面间的距离， kv ) t m -i2 exp( , (1) ∑ - 2 中 国 激 光 1 2 × expé i ù é ö PTæ ú ê ê ÷ ç ø è ë û ë R c t m - 2 m m 是沿光束传播轴的径向风速。 ，由大气参数组成，其可表示为 m [11] = exp( -2 | K | m ) β δ m m A R m 2 γ m , Δ R (2) 式中 PLO( φ 是相位函数，k 是波数，v 是一个圆随机变量 K m m-1·sr-1 式中 A 是接收望远镜的面积；R 为 是系统效率； exp( ；γ m -2 是每层中心与接收平面间的距离；β m ) δ m 是透射率。 在探测范围内，按仿真所需的风速细节设定 v 的取值情况，将系统参数代入 m 信号随时间或距离的变化关系。 2.2 信号时变特性分析 是后向散射系数随距离的分布，单位 m (1) 式就可得到仿真的回波 , t ) x 是时间的函数 随机信号在理论上可以分为平稳和非平稳两大类。非平稳信号是指统计特性随时间变化的随机信号， 式仿真得到的回波信号具有明显的时变特征，是非 其概率密度 P( 平稳信号。通过利用时间 t 的 Q 阶多项式来近似单次观测期间目标运动的径向速度，可以分析回波信号的 时变特性。假设径向速度的表达式为 (3) 。在探测时间内，由 =∑ [12] Q (1) (1) 式中 a q 是多项式系数。根据 = ( )t S m G( )t k m ( )t 式中 fo 为发射频率，λ 为波长，G( )t 和 k expæ è 式建立的回波信号数学模型，单层回波信号可表示为 - -i4π -i4π i2π = ( expé ) fo t R v t v t ö ø G( )t k m λ ( )t 代表模型系数。去掉载波信号及固定相位可得 λ m m m ë ) , ù û tq , a q v m = 0 q ( )t exp( ∑ Q (4) (5) (6) (7) (8) 假设目标运动的径向速度为线性，即 v ( )t s m m (6) 即在探测时间内 式表示的回波信号可看作是啁啾信号，其具有明显的时变特征，是非平稳信号。 傅里叶变换建立了信号从时域到频域的一一对应的映射关系，即 m ( )t s m q q a . tq λ = 0 ao + ù úú t û æ ç è ( ö ÷ ø ) a1t i4π = expé êê = + ë i4π a1t ，得到具有二次相位变化的回波信号为 = expé =∫ =∫ )exp(-i2π ( )exp(i2π )d )d ù t û ao λ ft ( , , . x ë t t X f ft f X( )f x( )t ∞ -∞ ∞ -∞ , 傅里叶变换将一个函数表示成无穷多个最和谐的函数—正弦函数的加权和 对信号的表征要么完全在 时域，要么完全在频域，不能揭示某种频率分量出现在什么时候以及随时间的变化情况。因此，常用的快速 - 傅里叶变换方法适于分析信号组成分量的频率不随时间变化的平稳信号。 频 域联合分析方法。时频分析方法通过分析时间、频率及能量之间的密切关系，提取信号中所包含的特征信 息，以揭示信号中所包含的频率分量及其演化特性 。时频分析能够确定特定时间有哪些频率成分存在，因 而在非平稳信号的分析领域得到广泛应用。 由以上分析，多普勒回波信号属于非平稳信号的分析领域。为了克服傅里叶变换的局限性，引入时 [13] 质。 子力学时提出的这种分布可表示为 分 布 是 常 用 的 时 频 分 析 方 法 ，在 已 提 出 的 各 种 时 频 分 布 中 ，形 式 简 洁 并 且 具 有 很 好 的 性 在研究量 分布具有明确的物理意义，可被看作信号能量在时域和频域中的分布。 (9) )=∫ Wigner )d [14] ( . , SWVD t f + τ2 s ∗æ è ö ø sæ è t - τ2 exp(-i2π t ö ø fτ τ Wigner-Ville Wigner-Ville 0114003- 3 ͂ ͂ ͂
    Wigner-Ville 通过加入核函数来抑制 由于 3 中 国 激 光 分布不是线性的，应用于大气分层模型时域仿真回波信号时会有交叉项产生，一般可 [12,15] Wigner-Ville ，如平滑伪 分布。 ( 为恒定值 回波信号仿真分析 2 m/s 首先对最简单的风速分布情况 Δ 进行分析，常风速是一种特殊的线性风速情况，在探测范围内令 60 m ，发射激光 PT 脉冲 ， 内的回波信号随距离的 所示。利用单个脉冲的回波信号来反演风速常因散斑效应中的随机相位的影响而产生偏 400 ns 各层的风速 v 200 宽度为 层数 M 为 变化曲线，如图 差。为了消除这种影响，可以先对多组脉冲进行累加平均再进行风速评估。 ) 所列系统参数，对于发射激光能量 Es 为 60~6000 m ，系统的采样频率为 1 常风速 200 MHz 。根据表 = 0.3 m ，探测器带宽 Bn 为 2 层，分层厚度 R 的系统，计算可得距离分辨率为 式仿真得到探测距离在 500 MHz 100 mJ 。利用 (1) m Parameter Value /μm 2 λ 相干测风激光雷达系统仿真参数 Table 1 System parameters used for simulation of coherent wind lidar /MHz 55 表 /(m-1·sr-1) 8 × 10-8 /mJ Es 100 /mW 1 m0.8 PLO υIF β δ m /mm 1100 A /MHz 200 Bn 1 对 相 干 测 风 激 光 雷 达 时 域 仿 真 回 波 信 号 进 行 功 率 谱 评 估 ，得 到 以 距 离 门 为 空 间 分 辨 率 的 一 维 风 速 信 ，得到第一个距离门 由快速傅里叶变换原理的风速反演算法 [16] , 息。选取第一个距离门 内回波信号的功率谱变换曲线，如图 为研究对象 所示。 3 γ m0.12 /ns PT 400 60~120 m 2 Fig.2 Curve of echo signal simulated with one pulse for the 常风速时单个发射脉冲的回波信号 图 constant wind velocity 2.27 MHz 功率谱峰值对应的频率 (52.73 MHz) 多普勒频移应为 法的自身精度，反演风速与给定的风速大小间有 模型对回波信号进行时域仿真的方法是可行的。 4 4.1 理想线性剪切风速的信号仿真与分析 应用时频变换反演风速 与声光频移量 υIF 0.27 m/s 。由多普勒测风原理可以反演得到径向风速为 3 Fig.3 Power spectrum of echo signal in first range gate for 图 常风速时第一个距离门内回波信号的功率谱 (55 MHz) constant wind velocity 2.27 m/s 的差值为多普勒频移，即给定风速造成的 。由于快速傅里叶变换算 的偏差。风速反演的误差较小，说明利用大气分层 通过描述风速细节，可将大气分层模型应用于非平稳的大气环境。下面对 v 为理想线性剪切风速时 1 50 m/s 所示。假定相干测风激光雷达在 4 距离内进行探测， 所示。将此线性变化的风速代入到大气分层模型 60~1200 m m 0 的回波信号进行仿真和验证，系统参数如表 忽略大气湍流的影响，风速从 线性增加到 的回波信号中，得到回波信号随着探测距离的变化曲线，如图 ( 2 与图 为线性剪切风速时，剪切风速随距离逐渐增大 ，如图 5 5 所示。 4) 对比图 相同。但 v 离逐渐增大。由于声光频移量 υIF 为固定值 可以看到，两图中回波信号都由于散斑的低频调制作用出现了随机起伏，变化趋势基本 ，由多普勒效应可知多普勒频移量也随距 ，因而信号的调制频率从近地面向探测远端逐渐降低，且 55 MHz 见图 m 0114003- 4
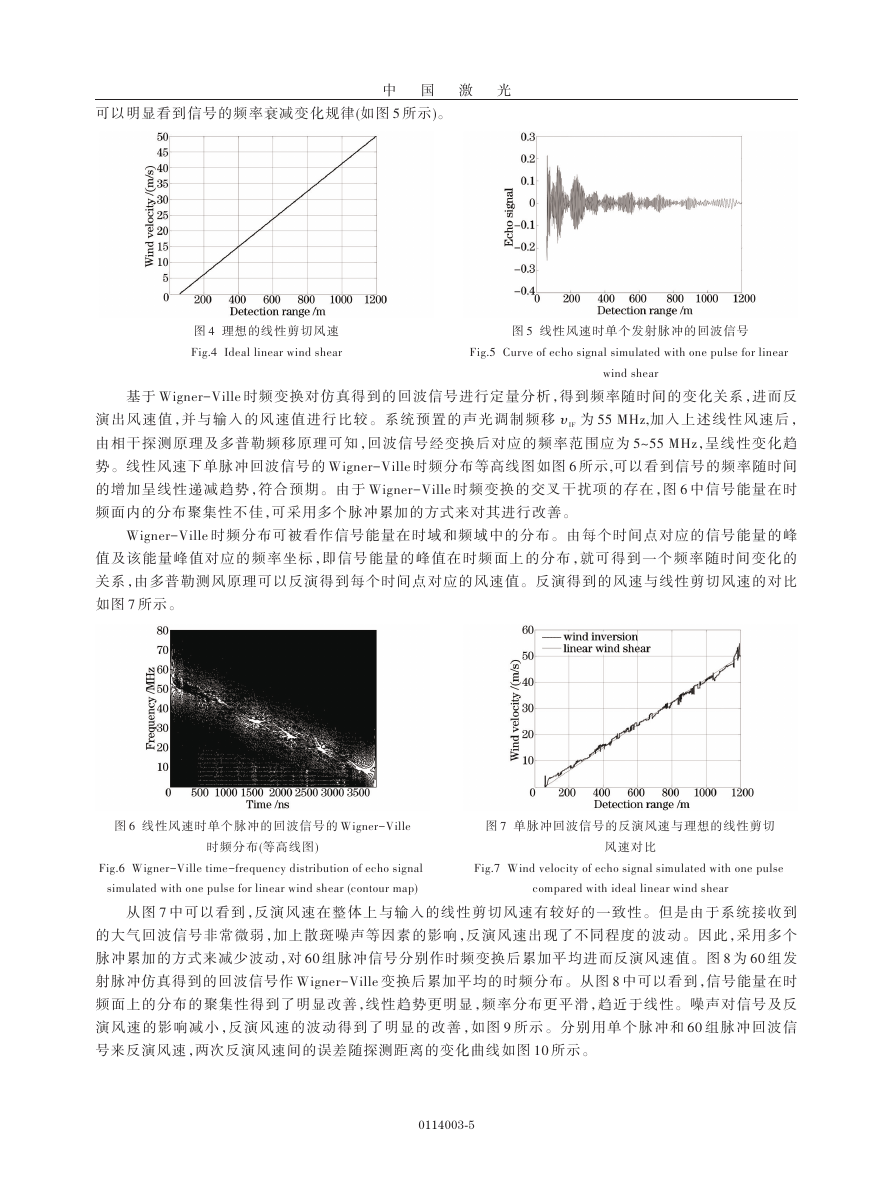
    5 中 国 激 光 ) 如图 所示 。 可以明显看到信号的频率衰减变化规律 ( 4 Fig.4 Ideal linear wind shear 图 理想的线性剪切风速 Wigner-Ville 基于 5 Fig.5 Curve of echo signal simulated with one pulse for linear 线性风速时单个发射脉冲的回波信号 图 wind shear 55 MHz, , 演出风速值，并与输入的风速值进行比较。系统预置的声光调制频移 υIF 为 由相干探测原理及多普勒频移原理可知，回波信号经变换后对应的频率范围应为 势。线性风速下单脉冲回波信号的 的增加呈线性递减趋势，符合预期。由于 频面内的分布聚集性不佳，可采用多个脉冲累加的方式来对其进行改善。 时频变换对仿真得到的回波信号进行定量分析，得到频率随时间的变化关系，进而反 加入上述线性风速后， ，呈线性变化趋 可以看到信号的频率随时间 中信号能量在时 5~55 MHz 6 时频变换的交叉干扰项的存在，图 Wigner-Ville Wigner-Ville 时频分布等高线图如图 所示 6 时频分布可被看作信号能量在时域和频域中的分布。由每个时间点对应的信号能量的峰 值及该能量峰值对应的频率坐标，即信号能量的峰值在时频面上的分布，就可得到一个频率随时间变化的 关系，由多普勒测风原理可以反演得到每个时间点对应的风速值。反演得到的风速与线性剪切风速的对比 如图 所示。 7 Wigner-Ville Wigner-Ville ( ) 线性风速时单个脉冲的回波信号的 Fig.6 Wigner-Ville time-frequency distribution of echo signal simulated with one pulse for linear wind shear (contour map) 时频分布 等高线图 6 图 7 7 图 单脉冲回波信号的反演风速与理想的线性剪切 Fig.7 Wind velocity of echo signal simulated with one pulse 风速对比 compared with ideal linear wind shear 从图 中可以看到，反演风速在整体上与输入的线性剪切风速有较好的一致性。但是由于系统接收到 的大气回波信号非常微弱，加上散斑噪声等因素的影响，反演风速出现了不同程度的波动。因此，采用多个 脉冲累加的方式来减少波动，对 组发 射脉冲仿真得到的回波信号作 中可以看到，信号能量在时 频面上的分布的聚集性得到了明显改善，线性趋势更明显，频率分布更平滑，趋近于线性。噪声对信号及反 演风速的影响减小，反演风速的波动得到了明显的改善，如图 组脉冲回波信 号来反演风速，两次反演风速间的误差随探测距离的变化曲线如图 组脉冲信号分别作时频变换后累加平均进而反演风速值。图 60 Wigner-Ville 变换后累加平均的时频分布。从图 所示。分别用单个脉冲和 所示。 60 10 60 为 9 8 8 0114003- 5
    中 国 激 光 8 60 Wigner-Ville 线性风速时 个脉冲的回波信号的 图 时频 Fig.8 Wigner-Ville time-frequency distribution of echo signal simulated with 60 pulses for linear wind shear (contour map) 等高线图 分布 ( ) 9 60 发射 图 个脉冲回波信号的反演风速与理想的线性剪切 Fig.9 Wind velocity of echo signal simulated with 60 pulses 风速对比 compared with ideal linear wind shear 10 60 图 Fig.10 Wind velocity′s errors between one pulse and 60 pulses for linear wind shear 组脉冲回波信号反演风速的误差 线性风速时分别由单脉冲和 4.2 NASA 阵风模型的信号仿真与分析 11) ，为了方便对比设风速最大值 Vmax 为 50 m/s 对基于实际观测值的大气风场进行仿真和验证。利用 半厚度。 = V Vmax2 { Vmax2 { ì ï ï Vmax í ï ï î π 1 - cosé 2 ë π 1 - cosé 2 ë h h ( y ( y , , } ) ù û - 2 Href - Href Href , Href Href } ) ù û d m < ≤ y ≤ + + 2 h d m (10) 式计算得到 NASA 的典型阵风模型 [17-18]( 见图 为阵风层的 ，Href 为参考高度位置，h 为变化的气层厚度，d - + m 将阵风模型代入到大气分层模型的回波信号中进行定量分析。图 为阵风模型下单个发射脉冲的回 . + 2 < d m Href - + 2 h d m Href < - y h h Href ≤ 12 y (10) 11 NASA 图 Fig.11 NASA typical wind shear model 的典型阵风模型 12 Fig.12 Curve of echo signal simulated with one pulse for NASA 阵风模型下单个发射脉冲的回波信号 图 typical wind shear model 0114003- 6
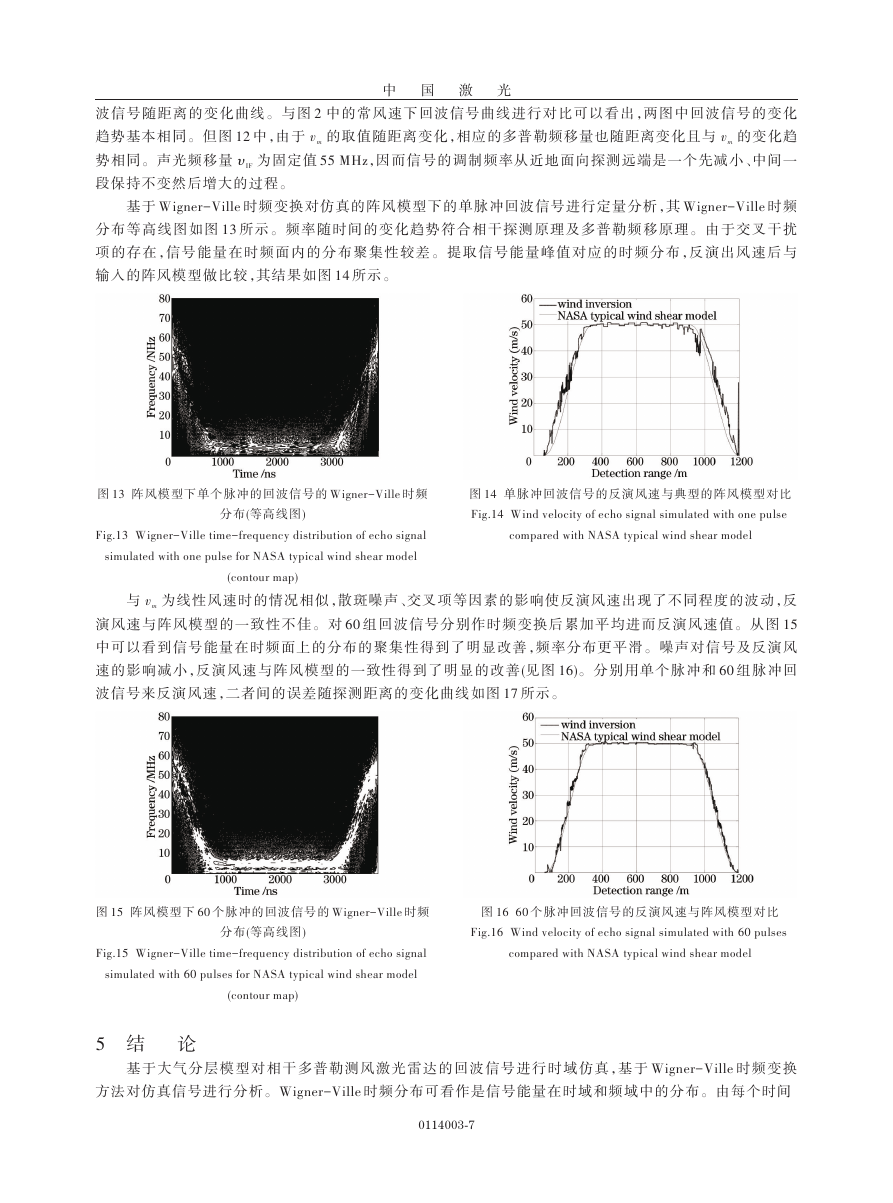
    2 中的常风速下回波信号曲线进行对比可以看出，两图中回波信号的变化 波信号随距离的变化曲线。与图 55 MHz 的取值随距离变化，相应的多普勒频移量也随距离变化且与 v 的变化趋 趋势基本相同。但图 中，由于 v ，因而信号的调制频率从近地面向探测远端是一个先减小、中间一 势相同。声光频移量 υIF 为固定值 段保持不变然后增大的过程。 中 国 激 光 12 m m 基于 时频变换对仿真的阵风模型下的单脉冲回波信号进行定量分析，其 时频 分布等高线图如图 所示。频率随时间的变化趋势符合相干探测原理及多普勒频移原理。由于交叉干扰 项的存在，信号能量在时频面内的分布聚集性较差。提取信号能量峰值对应的时频分布，反演出风速后与 输入的阵风模型做比较，其结果如图 所示。 14 Wigner-Ville 13 Wigner-Ville 13 Wigner-Ville 阵风模型下单个脉冲的回波信号的 图 时频 Fig.13 Wigner-Ville time-frequency distribution of echo signal simulated with one pulse for NASA typical wind shear model 等高线图 分布 ( ) (contour map) 14 Fig.14 Wind velocity of echo signal simulated with one pulse 单脉冲回波信号的反演风速与典型的阵风模型对比 图 compared with NASA typical wind shear model m 与 v 15 为线性风速时的情况相似，散斑噪声、交叉项等因素的影响使反演风速出现了不同程度的波动，反 演风速与阵风模型的一致性不佳。对 中可以看到信号能量在时频面上的分布的聚集性得到了明显改善，频率分布更平滑。噪声对信号及反演风 17 速的影响减小，反演风速与阵风模型的一致性得到了明显的改善 组脉冲回 波信号来反演风速，二者间的误差随探测距离的变化曲线如图 组回波信号分别作时频变换后累加平均进而反演风速值。从图 16) ( 见图 所示。 。分别用单个脉冲和 60 60 15 60 Wigner-Ville 阵风模型下 个脉冲的回波信号的 图 时频 Fig.15 Wigner-Ville time-frequency distribution of echo signal simulated with 60 pulses for NASA typical wind shear model 等高线图 分布 ( ) (contour map) 16 60 Fig.16 Wind velocity of echo signal simulated with 60 pulses 图 个脉冲回波信号的反演风速与阵风模型对比 compared with NASA typical wind shear model 5 结 论 基于大气分层模型对相干多普勒测风激光雷达的回波信号进行时域仿真，基于 Wigner-Ville 时频变换 时频分布可看作是信号能量在时域和频域中的分布。由每个时间 Wigner-Ville 方法对仿真信号进行分析。 0114003- 7
    中 国 激 光 17 60 Fig.17 Wind velocity′s errors between one pulse and 60 pulses for NASA typical wind shear model 组脉冲回波信号反演风速的误差 阵风模型下分别由单脉冲和 图 点对应的信号能量的峰值及该能量峰值对应的频率坐标，即信号能量的峰值在时频面上的分布，就可得到 一个频率随时间变化的关系，由多普勒测风原理可以反演得到每个时间点对应的风速值。大气情况分别为 线性风速和阵风模型时，仿真信号及反演风速经过验证有较为理想的结果。 与传统的快速傅里叶方法相比，时频分析方法在处理非平稳信号时有着明显的优势。快速傅里叶方法 对每个距离门内的信号序列作傅里叶变换及功率谱估计，全部数据算法流程包括距离门划分、功率谱估计、 累加去噪、频谱矫正等过程。而时频分析方法可以直接对多个距离门进行连续处理，快速得到不同探测时 间的频谱数值进而反演出相应的风速值。 由于散斑噪声、 时频变换交叉项等因素的影响，经时频变换反演得到的风速出现了不同程 个脉冲回波信号在 度的波动，可以采取多个脉冲累加平均的方式来改善。通过比较单个脉冲回波信号和 不同大气条件下反演风速的效果，可以看到经过累加平均处理的信号，其能量在时频面上的分布聚集性得 到了明显改善；反演风速的波动减小，反演风速与输入风速的一致性得到了明显的改善。 60 Wigner-Ville 1 Fujii Takashi. Laser Remote Sensing[M]. Florida: The Chemical Rubber Company Press, 2005. 2 Li Huang, Guo Jinjia. Development of space borne laser Doppler wind radar[C]. Chinese Meteorological Society 2006 Annual Meeting Proceedings, Cheng Du: 2006. 49-67. 参 考 文 献 [C]. 2006 , : 2006. 49-67. 成都 et al.. et al.. 郭金家 年年会论文集 中国气象学会 星载激光多普勒测风雷达发展研究 All fiber pulsed coherent lidar development for wind profiles measurements in boundary 3 Weifeng Diao, Xin Zhang, Jiqiao Liu, 李 黄 layers[J]. Chin Opt Lett, 2014, (7): 4 Salamitou Philippe, Dabas Alain, Flamant Pierre H. Simulation in the time domain for heterodyne coherent laser radar[J]. Appl Opt, 1995, 34(3): 499-506. 5 Kameyama S, Ando T, Asaka K, Performance of discrete-Fourier-transform-based velocity estimators for a wind-sensing coherent Doppler lidar system in the Kolmogorov turbulence regime[J]. IEEE Transactions on, Geoscience and Remote Sensing, 2009, 47(10): 3560-3569. 6 Rye B J, Hardesty R M. Discrete spectral peak estimation in incoherent backscatter heterodyne lidar. II. Correlogram accumulation [J]. IEEE Transactions on, Geoscience and Remote Sensing, 1993, 31(1): 28-35. 7 Zrnic D S. Spectral moment estimates from correlated pulse pairs[J]. IEEE Transactions on, Aerospace and Electronic Systems, 1977, AES-13(4): 344-354. 8 Frehlich Rod. Performance of maximum likelihood estimators of mean power and Doppler velocity with a priori knowledge of spectral width[J]. Journal of Atmospheric and Oceanic Technology, 1999, 16(11): 1702-1709. 9 Sui Xiaolin, Zhou Shouhuan, Zhao Hong, J Lasers, 2013, 40(12): 1208007. Research on an all-fiber structure velocity measurement coherent lidar[J]. Chinese et al.. , , . , 10 Li Yanchao. Study on Heterodyne Method and Key Technologies for 2-Micrometer Wind Lidar[D]. Harbin: Harbin Institute of 一种全光纤结构的相干激光测速雷达研究 中国激光 赵 鸿 等 [J]. , 2013, 40(12): 1208007. , . 眭晓林 周寿桓 Technology, 2012. 0114003- 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料