第1页 / 共329页
第2页 / 共329页
第3页 / 共329页
第4页 / 共329页
第5页 / 共329页
第6页 / 共329页
第7页 / 共329页
第8页 / 共329页
Principles of Communication 5Ed 习题答案.pdf
Chapter 2
Signal and Linear System Theory
2.1 Problem Solutions
Problem 2.1
For the single-sided spectra, write the signal in terms of cosines:
x(t) = 10 cos(4πt + π/8) + 6 sin(8πt + 3π/4)
= 10 cos(4πt + π/8) + 6 cos(8πt + 3π/4 − π/2)
= 10 cos(4πt + π/8) + 6 cos(8πt + π/4)
For the double-sided spectra, write the signal in terms of complex exponentials using Euler’s
theorem:
x(t) = 5 exp[(4πt + π/8)] + 5 exp[−j(4πt + π/8)]
+3 exp[j(8πt + 3π/4)] + 3 exp[−j(8πt + 3π/4)]
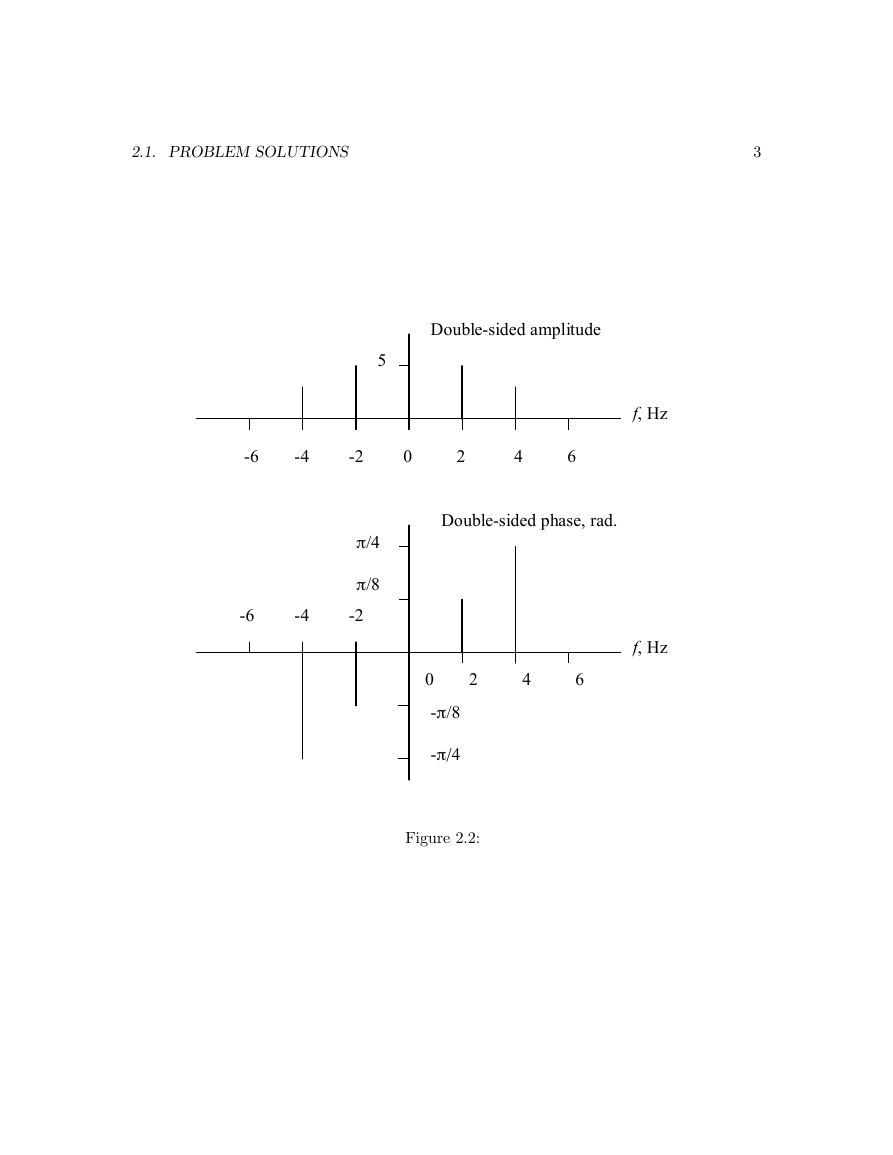
The two sets of spectra are plotted in Figures 2.1 and 2.2.
Problem 2.2
The result is
x(t) = 4ej(8πt+π/2) + 4e−j(8πt+π/2) + 2ej(4πt−π/4) + 2e−j(4πt−π/4)
= 8 cos (8πt + π/2) + 4 cos (4πt − π/4)
= −8 sin (8πt) + 4 cos (4πt − π/4)
1
2
10
5
CHAPTER 2. SIGNAL AND LINEAR SYSTEM THEORY
Single-sided amplitude
π/4
π/8
f, Hz
Single-sided phase, rad.
f, Hz
0 2 4 6
0 2 4 6
Figure 2.1:
Problem 2.3
(a) Not periodic.
(b) Periodic. To find the period, note that
6π
2π
= n1f0 and
20π
2π
= n2f0
Therefore
=
10
3
Hence, take n1 = 3, n2 = 10, and f0 = 1 Hz.
(c) Periodic. Using a similar procedure as used in (b), we find that n1 = 2, n2 = 7, and
f0 = 1 Hz.
(d) Periodic. Using a similar procedure as used in (b), we find that n1 = 2, n2 = 3, n3 = 11,
and f0 = 1 Hz.
n2
n1
Problem 2.4
(a) The single-sided amplitude spectrum consists of a single line of height 5 at frequency 6
Hz, and the phase spectrum consists of a single line of height -π/6 radians at frequency 6
Hz. The double-sided amplitude spectrum consists of lines of height 2.5 at frequencies of
6 and -6 Hz, and the double-sided phase spectrum consists of a line of height -π/6 radians
at frequency 6 Hz and a line of height π/6 at frequency -6 radians Hz.
(b) Write the signal as
xb(t) = 3 cos(12πt − π/2) + 4 cos(16πt)
From this it is seen that the single-sided amplitude spectrum consists of lines of height 3
and 4 at frequencies 6 and 8 Hz, respectively, and the single-sided phase spectrum consists
2.1. PROBLEM SOLUTIONS
3
Double-sided amplitude
5
-6 -4 -2 0 2 4 6
Double-sided phase, rad.
π/4
π/8
-6 -4 -2
f, Hz
f, Hz
0 2 4 6
-π/8
-π/4
Figure 2.2:
4
CHAPTER 2. SIGNAL AND LINEAR SYSTEM THEORY
of a line of height -π/2 radians at frequency 6 Hz. The double-sided amplitude spectrum
consists of lines of height 1.5 and 2 at frequencies of 6 and 8 Hz, respectively, and lines of
height 1.5 and 2 at frequencies -6 and -8 Hz, respectively. The double-sided phase spectrum
consists of a line of height -π/2 radians at frequency 6 Hz and a line of height π/2 radians
at frequency -6 Hz.
Problem 2.5
(a) This function has area
Area =
=
dt
(πt/²) ¸2
²−1· sin(πt/²)
∞Z−∞
(πu) ¸2
∞Z−∞ · sin(πu)
du = 1
A sketch shows that no matter how small ² is, the area is still 1. With ² → 0, the central
lobe of the function becomes narrower and higher. Thus, in the limit, it approximates a
delta function.
(b) The area for the function is
Area =
∞Z−∞
1
²
exp(−t/²)u (t) dt =
∞Z0
exp(−u)du = 1
A sketch shows that no matter how small ² is, the area is still 1. With ² → 0, the function
becomes narrower and higher. Thus, in the limit, it approximates a delta function.
(c) Area =R ²
−1 Λ (t) dt = 1. As ² → 0, the function becomes narrower
² (1 − |t| /²) dt =R 1
and higher, so it approximates a delta function in the limit.
1
−²
Problem 2.6
(a) 513; (b) 183; (c) 0; (d) 95,583.8; (e) -157.9.
Problem 2.7
(a), (c), (e), and (f) are periodic. Their periods are 1 s, 4 s, 3 s, and 2/7 s, respectively.
The waveform of part (c) is a periodic train of impulses extending from -∞ to ∞ spaced
by 4 s. The waveform of part (a) is a complex sum of sinusoids that repeats (plot). The
waveform of part (e) is a doubly-infinite train of square pulses, each of which is one unit
high and one unit wide, centered at · · ·, −6, −3, 0, 3, 6, · · ·. Waveform (f) is a raised
cosine of minimum and maximum amplitudes 0 and 2, respectively.
2.1. PROBLEM SOLUTIONS
5
Problem 2.8
(a) The result is
x(t) = Re¡ej6πt¢ + 6 Re³ej(12πt−π/2)´ = Rehej6πt + 6ej(12πt−π/2)i
(b) The result is
x(t) =
ej6πt +
1
2
1
2
e−j6πt + 3ej(12πt−π/2) + 3e−j(12πt−π/2)
(c) The single-sided amplitude spectrum consists of lines of height 1 and 6 at frequencies
of 3 and 6 Hz, respectively. The single-sided phase spectrum consists of a line of height
−π/2 at frequency 6 Hz. The double-sided amplitude spectrum consists of lines of height
3, 1/2, 1/2, and 3 at frequencies of −6, −3, 3, and 6 Hz, respectively. The double-sided
phase spectrum consists of lines of height π/2 and −π/2 at frequencies of −6 and 6 Hz,
respectively.
Problem 2.9
(a) Power. Since it is a periodic signal, we obtain
P1 =
1
T0Z T0
0
4 sin2 (8πt + π/4) dt =
1
T0Z T0
0
2 [1 − cos (16πt + π/2)] dt = 2 W
where T0 = 1/8 s is the period.
(b) Energy. The energy is
E2 =Z ∞
−∞
e−2αtu2(t)dt =Z ∞
0
e−2αtdt =
1
2α
(c) Energy. The energy is
E3 =Z ∞
−∞
e2αtu2(−t)dt =Z 0
−∞
e2αtdt =
1
2α
(d) Neither energy or power.
E4 = lim
T→∞Z T
−T
dt
(α2 + t2)1/4 = ∞
P4 = 0 since limT→∞
x2(t), its energy is the sum of the energies of these two signals, or E5 = 1/α.
(α2+t2)1/4 = 0.(e) Energy.
−T
Since it is the sum of x1(t) and
dt
1
T R T
6
CHAPTER 2. SIGNAL AND LINEAR SYSTEM THEORY
(f) Power. Since it is an aperiodic signal (the sine starts at t = 0), we use
P6 = lim
T→∞
= lim
T→∞
0
1
2T Z T
2T · T
1
sin2 (5πt) dt = lim
T→∞
1
2
sin (20πt)
20π
2 −
=
W
1
4
¸T
0
1
2T Z T
0
1
2
[1 − cos (10πt)] dt
Problem 2.10
(a) Power. Since the signal is periodic with period π/ω, we have
ω
πZ π/ω
P =
A2 |sin (ωt + θ)|2 dt =
(b) Neither. The energy calculation gives
0
ω
πZ π/ω
0
A2
2 {1 − cos [2 (ωt + θ)]} dt =
A2
2
E = lim
T→∞Z T
−T
(Aτ )2 dt
√τ + jt√τ − jt
The power calculation gives
1
2T Z T
−T
(Aτ )2 dt
√τ 2 + t2
= lim
T→∞
P = lim
T→∞
(c) Energy:
(Aτ )2
2T
= lim
−T
(Aτ )2 dt
√τ 2 + t2 → ∞
T→∞Z T
lnà 1 +p1 + T 2/τ 2
−1 +p1 + T 2/τ 2! = 0
E =Z ∞
0
A2t4 exp (−2t/τ ) dt =
3
4
A2τ 5 (use table of integrals)
(d) Energy:
E = 2ÃZ τ /2
0
22dt +Z τ
τ /2
12dt! = 5τ
Problem 2.11
(a) This is a periodic train of “boxcars”, each 3 units in width and centered at multiples of
6:
Pa =
1
6Z 3
−3
Π2µ t
3¶ dt =
1
6Z 1.5
−1.5
dt =
1
2
W
2.1. PROBLEM SOLUTIONS
7
(b) This is a periodic train of unit-high isoceles triangles, each 4 units wide and centered
at multiples of 5:
Pb =
1
5Z 2.5
−2.5
Λ2µ t
2¶ dt =
2
0 µ1 −
5Z 2
t
2¶2
dt = −
2
5
2
3µ1 −
2
0
=
4
15
W
(c) This is a backward train of sawtooths (right triangles with the right angle on the left),
each 2 units wide and spaced by 3 units:
t
2¶3¯¯¯¯¯
(d) This is a full-wave rectified cosine wave of period 1/5 (the width of each cosine pulse):
Pc =
1
0 µ1 −
3Z 2
t
2¶2
dt = −
1
3
2
3µ1 −
Pd = 5Z 1/10
−1/10 |cos (5πt)|2 dt = 2 × 5Z 1/10
0
· 1
2
+
0
2
t
=
2
9
W
2¶3¯¯¯¯¯
cos (10πt)¸ dt =
1
2
1
2
W
Problem 2.12
(a) E = ∞, P = ∞; (b) E = 5 J, P = 0 W; (c) E = ∞, P = 49 W; (d) E = ∞, P = 2 W.
Problem 2.13
(a) The energy is
(b) The energy is
+
−6
E =Z 6
−∞he−|t|/3 cos (12πt)i2
0 · 1
cos2 (6πt) dt = 2Z 6
dt = 2Z ∞
2
0
1
2
cos (12πt)¸ dt = 6 J
e−2t/3· 1
1
2
+
2
cos (24πt)¸ dt
E =Z ∞
where the last integral follows by the eveness of the integrand of the first one. Use a table
of definte integrals to obtain
E =Z ∞
0
e−2t/3dt +Z ∞
0
e−2t/3 cos (24πt) dt =
3
2
+
2/3
(2/3)2 + (24π)2
Since the result is finite, this is an energy signal.
(c) The energy is
E =Z ∞
−∞ {2 [u (t) − u (t − 7)]}2 dt =Z 7
0
4dt = 28 J
8
CHAPTER 2. SIGNAL AND LINEAR SYSTEM THEORY
Since the result is finite, this is an energy signal.
(d) Note that
which is called the unit ramp. The energy is
−∞
Z t
u (λ) dλ = r (t) =½ 0, t < 0
10¶2
0 µ t
[r (t) − 2r (t − 10) + r (t − 20)]2 dt = 2Z 10
t, t ≥ 0
E =Z ∞
−∞
dt =
20
3
J
where the last integral follows because the integrand is a symmetrical triangle about t = 10.
Since the result is finite, this is an energy signal.
Problem 2.14
(a) Expand the integrand, integrate term by term, and simplify making use of the orthog-
onality property of the orthonormal functions.
(b) Add and subtract the quantity suggested right above (2.34) and simplify.
(c) These are unit-high rectangular pulses of width T /4.
T /8, 3T /8, 5T /8, and 7T /8.
other and fill the interval [0, T ].
(d) Using the expression for the generalized Fourier series coefficients, we find that X1 =
1/8, X2 = 3/8, X3 = 5/8, and X4 = 7/8. Also, cn = T /4. Thus, the ramp signal is
approximated by
They are centered at t =
Since they are spaced by T /4, they are adjacent to each
t
T
=
1
8
φ1 (t) +
3
8
φ2 (t) +
5
8
φ3 (t) +
7
8
φ4 (t) , 0 ≤ t ≤ T
where the φn (t)s are given in part (c).
(e) These are unit-high rectangular pulses of width T /2 and centered at t = T /4 and 3T /4.
We find that X1 = 1/4 and X2 = 3/4.
(f) To compute the ISE, we use
²N =ZT |x (t)|2 dt −
NXn=1
cn¯¯X 2
n¯¯
64¢ = 5.208 × 10−3T .
16¢ = 2.083 × 10−2T .
0 (t/T )2 dt = T /3. Hence, for (d),
64 + 25
64 + 49
16 + 9
Note thatRT |x (t)|2 dt =R T
4¡ 1
64 + 9
3 − T
2¡ 1
3 − T
ISEd = T
For (e), ISEe = T
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
