第 17 卷第 1 期 2004 年 3 月 青岛职业技术学院学报 Journal of Q ingdao V ocational and T echnical College V ol. 17 N o. 1 M ar. 2004 线性二次型最优控制器的 M AT LAB 实现 金龙国, 王 娟 ( 青岛职业技术学院 信息技术学院, 山东 青岛 266555) 摘要: 本文通过事例介绍了利用 M AT L AB 设计线性二次型最优控制器问题的基本方法, 并讨论了参数变 化对最优控制系统的影响。 关键词: MA T LA B; 线性二次型; 最优控制器 中图分类号: T P 273. 1 文献标识码: A 文章编号: 1672- 2698( 2004) 01- 0036- 02 对于线性定常系统, 当 tf 终值时间时, P 为常数 矩阵, 它可以通过下面的李卡蒂代数方程解得: PA + A TP-PBR- 1BT P + Q = 0 此时, 线性二次型指标 J 的表达式中不包含末值项, 其最优控制为 m * ( t ) = -kX ( t ) = -R-1 BTPX ( t ) 式中反馈系数矩阵 k 为常数矩阵。 二、最优控制器的设计 本文通过具体实例介 绍在 MAT LAB 环境 下设 计一个线性二次型最优控制器的过程和方法。由于 代数李卡蒂方程求解过程中仅涉及矩阵运算, 所以很 适合用 MA T LA B 软件处理, 在 MA T LA B 的 控制系 统分析与设计工具箱中提供了求解代数李卡蒂方程 的函数 l qr ( ) , 其调用方法如下: K , P , E = lqr ( A , B, Q , R ) 其中矩阵 A , B , Q , R 的意义如前所述, 返回的 K 矩 阵为状态反馈矩阵, P 为李卡蒂方程的解, E 为闭环 系统的极点。 举例: 已知系统的状态方程如下 0 0 1 0 0 1 X + X = 0 - 2 - 3 Y = [ 1 0 0 ] X 0 0 1 U 以线性二次型性能指标为基础的最优控制问题 是 20 世纪 50 年代末期发展起来的一种设计控制系 统的方法, 这种方法具有计算简单, 便于调整等优点, 因线性二次型问题解出的控制规律可以通过状态反 馈实现闭环最优控制, 而成为当今控制工程领域里较 为重要的设计方法之一。 M AT L AB 软件是美国 Works 公司于 1984 年推 出的高效率的数值计算和可视化 软件, 它集 数值分 析、矩阵运算、图形绘制、数据处理、图象处理于一体, 具有编程简单、使用方便等特点, 此外, 它还带有许多 强大的具有特殊功能的工具箱。MA T LA B 是目前国 际最流行的控制系统计算机辅助设计语言和软件工 具。 本文在 MAT LAB6. 0 基础上, 讨论在 工程中实 际应用最广泛、最一般的最优控制问题的设计方法。 一、线性二次型最优控制与李卡蒂方程 假设线性时不变系统的状态空间描述为 X = A X + Bu y = AX + Bu 若系统满足的性能指标为线性二次型, 即 J = T 1 2 X ( tf ) SX ( tf ) + 1 2tf 0 X T ( t ) Q ( t ) X ( t ) + u T ( t ) R ( t ) u ( t ) dt 其中 Q ( t ) 和 R ( t ) 分别是对状态变量和输入量的加 权矩阵, S 为半 正定常数矩阵。在输入信号 无约束 时, 则最优控制为线性, 其表达式如下: m * ( t ) = -k ( t ) X ( t ) = -R- 1( t ) BT ( t ) P ( t ) X ( t ) 式中 k ( t ) 为状态反馈系数矩阵, 它可以用下面的式 子描述: 性能指标为 J = Q = a 1 0 0 0 X T QX + uT R u dt , 其中 Q , R 为 0 0 R = [ 0. 01] a 2 0 0 a 3 K ( t ) = R -1 T ( t ) B ( t ) P( t ) 要求设计状态反馈控制器, 使 J 最小。 收稿日期: 2003- 10- 22 作者简介: 金龙国( 1963- ) , 男, 吉林和龙人, 副教授, 硕士。 36 

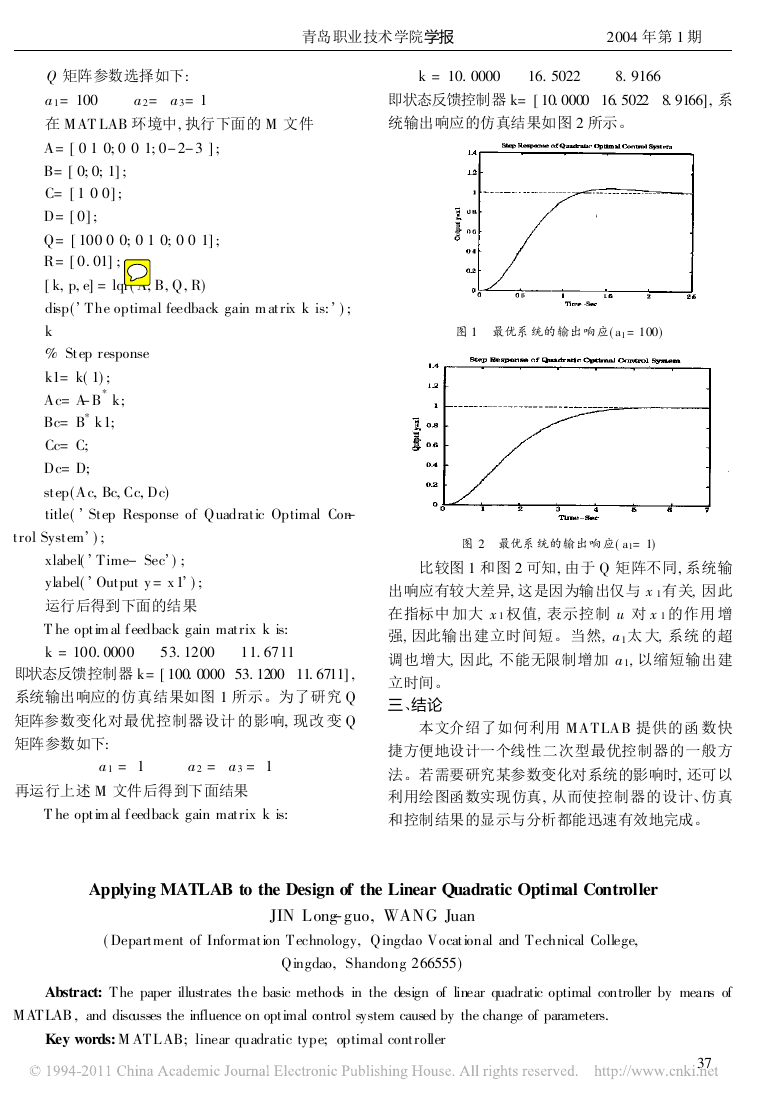
青岛职业技术学院学报 2004 年第 1 期 k = 10. 0000 即状态反馈控制器 k= [ 10. 0000 16. 5022 8. 9166] , 系 统输出响应的仿真结果如图 2 所示。 16. 5022 8. 9166 图 1 最优系统的输出响应( a1 = 100) Q 矩阵参数选择如下: a 1= 100 在 MAT LAB 环境中, 执行下面的 M 文件 a 2= a 3= 1 A = [ 0 1 0; 0 0 1; 0- 2- 3 ] ; B= [ 0; 0; 1] ; C= [ 1 0 0] ; D = [ 0] ; Q = [ 100 0 0; 0 1 0; 0 0 1] ; R = [ 0. 01] ; [ k, p, e] = lqr( A, B, Q , R) disp( T he optimal feedback gain m at rix k is: ) ; k % St ep response k1= k( 1) ; * A c= A- B Bc= B* k1; Cc= C; k; D c= D; st ep( A c, Bc, Cc, D c) title( St ep Response of Q uadrat ic Optimal Con- t rol Syst em ) ; xlabel( T ime- Sec ) ; ylabel( Out put y = x 1 ) ; 运行后得到下面的结果 T he opt im al f eedback gain mat rix k is: k = 100. 0000 53. 1200 11. 6711 即状态反馈控制器 k= [ 100. 0000 53. 1200 11. 6711] , 系统输出响应的仿真结果如图 1 所示。为了研究 Q 矩阵参数变化对最优控制器设计 的影响, 现改 变 Q 矩阵参数如下: a 1 = 1 a 2 = a 3 = 1 再运行上述 M 文件后得到下面结果 T he opt im al f eedback gain mat rix k is: 图 2 最优系统的输出响应( a1= 1) 比较图 1 和图 2 可知, 由于 Q 矩阵不同, 系统输 出响应有较大差异, 这是因为输出仅与 x 1有关, 因此 在指标中 加大 x 1 权值, 表示控制 u 对 x 1 的作用 增 强, 因此输出建立时间短。当然, a 1太 大, 系统 的超 调也增大, 因此, 不能无限制增加 a 1, 以缩短输出建 立时间。 三、结论 本文介绍了如何利用 MA T LA B 提供的函 数快 捷方便地设计一个线性二次型最优控制器的一般方 法。若需要研究某参数变化对系统的影响时, 还可以 利用绘图函数实现仿真, 从而使控制器的设计、仿真 和控制结果的显示与分析都能迅速有效地完成。 Applying MATLAB to the Design of the Linear Quadratic Optimal Controller JIN L ong- guo, WANG Juan ( Depart ment of Informat ion T echnology, Q ingdao V ocat ional and T echnical College, Q ingdao, Shandong 266555) Abstract: T he paper illustrates the basic methods in the design of linear quadratic optimal controller by means of MAT LAB , and discusses the influence on opt imal control system caused by the change of parameters. Key words: M AT L AB; linear quadratic type; optimal cont roller 37