2022年山西朔州中考数学试卷及答案.doc-资料库

第1页 / 共13页

第2页 / 共13页

第3页 / 共13页

第4页 / 共13页

第5页 / 共13页

第6页 / 共13页

第7页 / 共13页

第8页 / 共13页

2022年山西朔州中考数学试卷及答案一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑） 1．﹣6的相反数为（） A．6 B． C． D．﹣6 2．2022年4月16日，神舟十三号载人飞船圆满完成全部既定任务，顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度下列航天图标，其文字上方的图案是中心对称图形的是（） A． B． C． D． 3．粮食是人类赖以生存的重要物质基础.2021年我国粮食总产量再创新高，达68285万吨.该数据可用科学记数法表示为（） A．6.8285×104吨 C．6.8285×107吨 B．68285×104吨 D．6.8285×108吨 4．神奇的自然界处处蕴含着数学知识.动物学家在鹦鹉螺外壳上发现，其每圈螺纹的直径与相邻螺纹直径的比约为 0.618.这体现了数学中的（） A．平移 B．旋转 C．轴对称 D．黄金分割 5．不等式组的解集是（） A．x≥1 B．x＜2 C．1≤x＜2 D．x＜ 6．如图，Rt△ABC是一块直角三角板，其中∠C=90°，∠BAC=30°. 直尺的一边DE经过顶点A，若DE∥CB，则∠DAB 的度数为（） A．100° B．120° C．135° D．150° 7．化简 ﹣ 的结果是（） A． B．a﹣3 C．a+3 D．

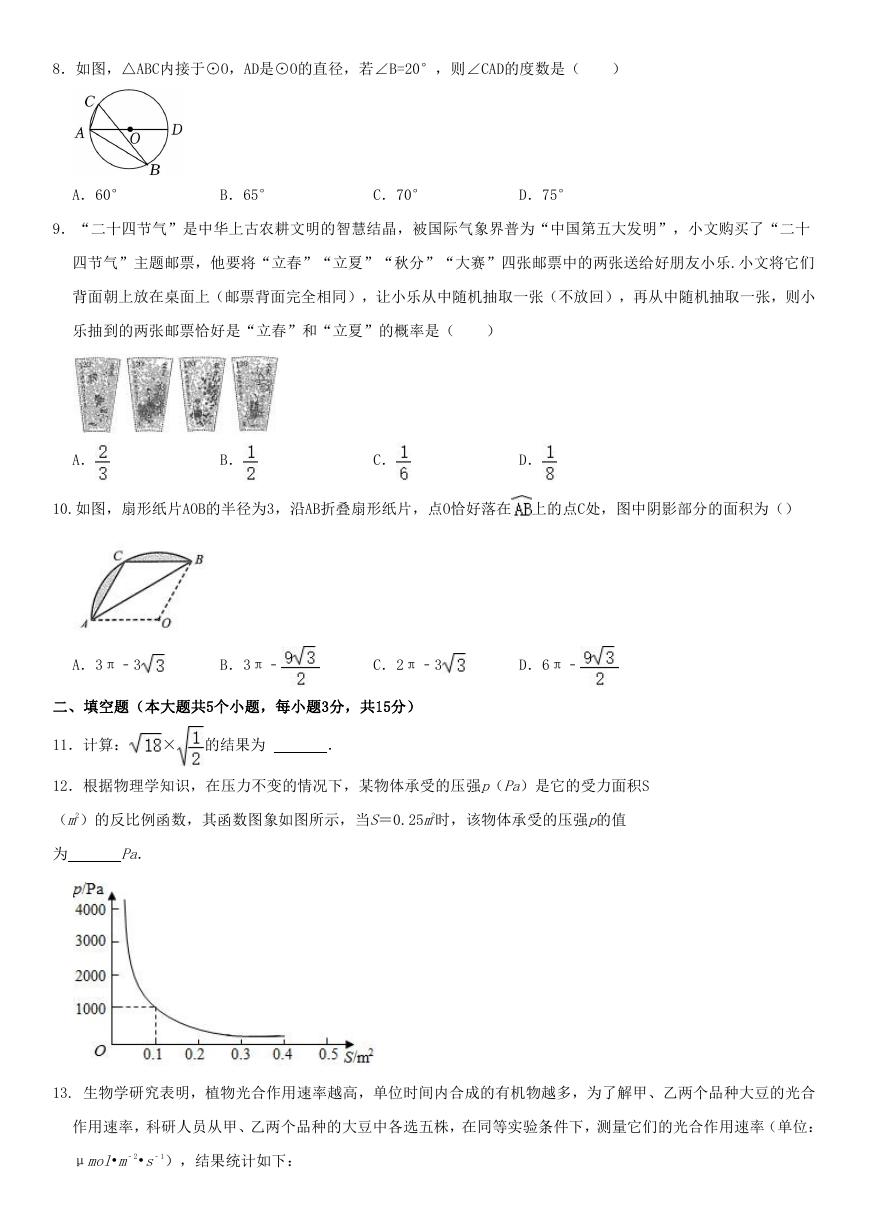
8．如图，△ABC内接于⊙O，AD是⊙O的直径，若∠B=20°，则∠CAD的度数是（） A．60° B．65° C．70° D．75° 9．“二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界普为“中国第五大发明”，小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大赛”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上（邮票背面完全相同），让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（） A． B． C． D． 10.如图，扇形纸片AOB的半径为3，沿AB折叠扇形纸片，点O恰好落在上的点C处，图中阴影部分的面积为（） A．3π﹣3 B．3π﹣ C．2π﹣3 D．6π﹣ 二、填空题（本大题共5个小题，每小题3分，共15分） 11．计算： × 的结果为． 12．根据物理学知识，在压力不变的情况下，某物体承受的压强p（Pa）是它的受力面积S （m2）的反比例函数，其函数图象如图所示，当S＝0.25m2时，该物体承受的压强p的值为 Pa． 13. 生物学研究表明，植物光合作用速率越高，单位时间内合成的有机物越多，为了解甲、乙两个品种大豆的光合作用速率，科研人员从甲、乙两个品种的大豆中各选五株，在同等实验条件下，测量它们的光合作用速率（单位： μmol•m﹣2•s﹣1），结果统计如下：

品种第一株第二株第三株第四株第五株平均数甲乙 32 28 30 25 25 26 18 24 20 22 25 25 则两个大豆品种中光合作用速率更稳定的是（填“甲”或“乙”）． 14.某品牌护眼灯的进价为240元，商店以320元的价格出售.“五一节”期间，商店为让利于顾客，计划以利润率不低于20%的价格降价出售，则该护眼灯最多可降价元． 15.如图，在正方形ABCD中，点E是边BC上的一点，点F在边CD的延长线上，且BE=DF，连接EF交边AD于点G.过点A作 AN⊥EF，垂足为点M，交边CD于点N.若BE=5，CN=8，则线段AN的长为三、解答题（本大题共8个小题，共75分．解答应写出文字说明，证明过程或演算步骤） 16．（1）计算：（﹣3）2×3﹣1+（﹣5+2）+|﹣2|；（2）解方程组：． 17.如图，在矩形ABCD中，AC是对角线. （1）实践与操作：利用尺规作线段AC的垂直平分线，垂足为点O，交边AD于点E，交边BC于点F（要求：尺规作图并保留作图痕迹，不写作法，标明字母），（2）猜想与证明：试猜想线段AE与CF的数量关系，并加以证明. 18.2022年我国已成为全球最大的电动汽车市场，电动汽车在保障能源安全，改善空气质量等方面较传统汽车都有

明显优势，经过对某款电动汽车和某款燃油车的对比调查发现，电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元.若充电费和加油费均为200元时，电动汽车可行驶的总路程是燃油车的4倍，求这款电动汽车平均每公里的充电费. 19.首届全民阅读大会于2022年4月23日在北京开幕，大会主题是“阅读新时代·奋进新征程”.某校“综合与实践” 小组为了解全校3600名学生的读书情况，随机抽取部分学生进行问卷调查，形成了如下调查报告（不完整）： ××中学学生读书情况调查报告 ××中学学生读书情况抽样调查调查对象 ××中学学生调查主题调查方式数据第一项您平均每周阅的收集、整理与描述读课外书的时间大约是（只能单选，每项含最小值，不含最大值） A.8小时及以上； B.6～8小时； C.4～6小时； D.0～4小时．第二项您阅读的课外书的主要来源是（可多选） E．自行购买； F．从图书馆借阅； G．免费数字阅读；

H．向他人借阅． …… 调查结论请根据以上调查报告，解答下列问题：（1）求参与本次抽样调查的学生人数及这些学生中选择“从图书馆借阅”的人数；（2）估计该校3600名学生中，平均每周阅读课外书时间在“8小时及以上”的人数；（3）该小组要根据以上调查报告在全班进行交流，假如你是小组成员，请结合以上两项调查数据分别写出一条你获取的信息. 20．阅读与思考下面是小宇同学的数学小论文，请仔细阅读并完成相应的任务用函数观点认识一元二次方程根的情况我们知道，一元二次方程ax2+bx+c＝0（a≠0）的根就是相应的二次函数y＝ax2+bx+c（a ≠0）的图象（称为抛物线）与x轴交点的横坐标．抛物线与x轴的交点有三种情况：有两个交点、有一个交点、无交点. 与此相对应，一元二次方程的根也有三种情况：有两个不相等的实数根、有两个相等的实数根、无实数根.因此可用抛物线与x轴的交点个数确定一元二次方程根的情况下面根据抛物线的顶点坐标（﹣ ，）和一元二次方程根的判别式Δ＝b2﹣4ac，分别分a＞0和a＜0两种情况进行分析：（1）a＞0时，抛物线开口向上． ①当Δ＝b2﹣4ac＞0时，有4ac﹣b2＜0．∵a＞0，∴顶点纵坐标＜0． ∴顶点在x轴的下方，抛物线与x轴有两个交点（如图1）． ②当Δ＝b2﹣4ac＝0时，有4ac﹣b2＝0．∵a＞0，∴顶点纵坐标＝0． ∴顶点在x轴上，抛物线与x轴有一个交点（如图2）． ∴一元二次方程ax2+bx+c＝0（a≠0）有两个相等的实数根． ③当Δ＝b2﹣4ac＜0时， …… （2）a＜0时，抛物线开口向下．

…… 任务：（1）上面小论文中的分析过程，主要运用的数学思想是（从下面选项中选出两个即可）； A．数形结合 B．统计思想 C．分类讨论 D．转化思想（2）请参照小论文中当a＞0时①②的分析过程，写出③中当a＞0，Δ＜0时，一元二次方程根的情况的分析过程，并画出相应的示意图；（3）实际上，除一元二次方程外，初中数学还有一些知识也可以用函数观点来认识，例如：可用函数观点来认识一元一次方程的解.请你再举出一例为 21.随着科技的发展，无人机已广泛应用于生产和生活，如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测星AB，CD两座楼之间的距离，他们借助无人机设计了如下测量方案：无人机在AB，CD两楼之间上方的点O处，点O距地面AC的高度为60m，此时观测到楼AB底部点A处的俯角为70°，楼CD上点E处的俯角为30°，沿水平方向由点O飞行24到达点F，测得点E处俯角为60°，其中点A，B，C，D，E，F，O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长（结果精确到1m．参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈ 2.75， ≈1.73）． 22.综合与实践问题情境：在Rt△ABC中，∠BAC=90°，AB=6，AC=8.直角三角板EDF中∠EDF=90°，将三角板的直角顶点D放在Rt△ ABC斜边BC的中点处，并将三角板绕点D旋转，三角板的两边DE，DF分别与边AB，AC交于点M，N，猜想证明：（1）如图①，在三角板旋转过程中，当点M为边AB的中点时，试判断四边形AMDN的形状，并说明理由；问题解决：（2）如图②，在三角板旋转过程中，当∠B=∠MDB时，求线段CN的长；（3）如图③，在三角板旋转过程中，当AM=AN时，直接写出线段AN的长.

23.综合与探究如图，二次函数y＝﹣ x2+ x+4的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点P是第一象限内二次函数图象上的一个动点，设点P的横坐标为m.过点P作直线PD⊥x轴于点D，作直线BC交PD于点E （1）求A，B，C三点的坐标，并直接写出直线BC的函数表达式；（2）当△CEP是以PE为底边的等腰三角形时，求点P的坐标；（3）连接AC，过点P作直线l ∥AC，交y轴于点F，连接DF.试探究：在点P运动的过程中，是否存在点P，使得CE=FD，若存在，请直接写出m的值；若不存在，请说明理由.

资料库

2022年山西朔州中考数学试卷及答案.doc

相关推荐

中考

热门标签

最新资料