西北工业大学计算方法习题答案.pdf-资料库

=1.7； 2x * =1.73； 3x * =1.732 。 1x * 1 2． i 1 2 3 4 5 ix * 1x * 2x * 3x * 4x * 5x * ixε ( * ) 1 2 010 × 1 2 1 2 1 2 1 2 510 −× 110 −× 210 −× 510 −× 参考答案第一章 r xε ( * i ) × × × .0 310 1397 .0 − 0.1666×10－3 1051 .0 210 − 0.125×10－2 3497 310 − 0.5×10－3 1691 310 − 0.25×10－3 8548 610 − 0.1×10－6 .0 .0 × × 或或或或或有效数字的位数四位三位四位四位六位 0.00050； ≤ 3．（1）（2） xer x x ) ( * * * + + 3 1 2 xxxer ( ≤) * * * 0.50517； 2 1 3 2 x xer / ≤) ( * * 4 n 0.50002。（3） 4．设 6 有位有效数字，由 6 ≈2.4494……，知 6 的第一位有效数字 =2。 1a 令 * xε ( r ) = 1 a 2 1 × 10 n ( −− )1 = 1 22 × n ( −− )1 × 10 ×≤ 1 2 − 3 10 可求得满足上述不等式的最小正整数 =4，即至少取四位有效数字，故满足精度要求可取 5. 答：（1） *x ( （2） ( )的相对误差约是的相对误差的 1/2 倍；的相对误差约是的相对误差的倍。 0>x nx )* *x *x n n 6 ≈2.449。 1 2 + * sin bec ( * * ) ba ** sin c * cos cec ( * * ) ba ** sin c * ba ** 1 2 * sin aec ( * * ) ba ** sin c * + b 1 2 ) * ae ( a * + ) * be ( b * + ce ( * tgc 6．根据 Ser ( * ) ≤ 1 2 = 注意当 0 < c 则有 Se ( r * ) * π < 2 ae ( r < 1 2 a 1 2 ) * ce ( r 1 2 ， ×≤ δ1 时，tgc * * > c > ，即0 tgc ( * ) 1 − < c ( * ) − 1 。 * ) + * be ( r ) + * ) 7．设由 0 =y y 1 2 ， − y * 1 0 =y ，41.1* 10 − y = − 1 0 y 0 − y * 0 y * 0 ≤ 10 − −2 10 δ= 1

y * 10 1 − y 10 − = δ时，的绝对误差的绝对值将减小10 倍。而10 10− ≤ δ10 10 * 9 − y 9 10y 10 << − δ 1 ，故计算过程稳定。 2 − )1 1 xx ( 1 NN ln + + )1 − =1 ln( N − = ( N + )1 1ln( + NN ln − 1 = N 1ln( y * 2 = 10 − 1 y 1 − y * 1 ≤ 10 − δ2 y 2 − M y − 10 0y 即当有初始误差 8. 变形后的表达式为： )1 （1） = − x 2 − ln( x − ln( x + x （2） arctg ( x −+ )1 arctgx = arctg （3） N ln1 ∫ + N dxx = ( N + )1 ln( x cos x sin （4） 1− = x sin cos + 1 x = N )1 + )1 + N xtg 2 1．绝对误差限 1 10 − 31 × 2 n 1 2 3 4 5 6 7 8 , 对分 8 次隔根区间 [1.5，2.5] [2.0，2.5] [2.25，2.5] [2.25，2.375] [2.25，2.3125] [2.28125，2.3125] [2.296875，2.3125] [2.296875，2.3046875] 满足精度要求的根近似值为 2.30。 2． (1) 隔根区间[0, 0.8]； 2ln( (2) 等价变形 (3) 收敛性论证：用收敛性定理论证。；迭代公式 − = x x ) (4) 迭代计算： )1 1 −+ N 2 )1 N + + 2 1 N 3 N + − 1 N 4 1)1 − + ln( LL+ 3 第二章 nx 2.0 2.25 2.375 2.3125 2.28125 2.296875 2.3046875 2.30078125 ( nxf ) 的符号        x n = 2ln( − x ) n 1 − n = 。 L,2,1 n 0 1 2 3 4 5 6 7 8 9 10 11 nx 0.4 0.4700 0.4253 0.4541 0.4356 0.4475 0.4399 0.4448 0.4416 0.4436 0.4423 0.4432 1− x n x − n 2/)7 ； (3) x 3 = x 1+ ；满足要求的近似根为 0.443。 3． (1) ； (2) x 210 − = = x x 7 (lg + x 2

4． f x )( ′ = 2 3 x + 4 x + 1 牛顿迭代公式为： x =+ 1 n x n − xf ( n f x ( ′ n ) ) LL= 列表计算根的近似值为 0.4656。 n 0 1 2 3 nx 0.4 0.47013 0.46559 0.46557 第三章 x n 1− x − n 0.07 0.005 0.00002         0 2． 1A =− 1． x1=2，x2=1，x3=1/2 1 3 2 − 3 1 3 1   3  1 0  3  21   3  001     012   15 3     3． L = − − − ， U = 321   10 4 −  00 24  −       y1 =14, y2 = −10, y3 = −72 x1 =1, x2 =2, x3 =3 4. x1≈-4.00, x2≈3.00, x3≈2.00 5. B 的特征值为：0，0，0，ρ(B)=0<1 (E－B1)-1B2 的特征值为：0，2，2，ρ[(E－B1)-1B2]=2>1. 6. x(5)=(0.4999, 1.0004, -0.4997)T 7.∣a∣>2 第四章 1. k u = u k A 1−k 0 1 2 3 4 5 6 5615 ( 1 , 1 , 1 ) T ( 4 , 2 , 4 ) T T ( 14 , 8 , 14 ) T ( 50 , 28 , 50 ) ( 178 , 100 , 178 ) T ( 634 , 356 , 634 ) T ( 2258 , 1268 , 2258 ) T )7( 1 ≈λ .3 相应近似特征向量为 c = 2258 ， 1268 ， 2258 ） T ，（ ( ) k ( λ 1 = u ( u ( k k ) 1 ) 11 − 4.0000 3.5000 3.5714 3.5600 3.5618 3.5615 3.5615 0≠c ） 0x 0x 1．取 =100、 =121 用线性插值时，取 =100、 =121、 =144 用二次插值时， 2．选取插值节点为： =1.4、 =1.5、 =1.6， 2x 1x 1x 2x 0x 1x 第五章 115 ≈10.7143； 115 ≈10.7228。 )54.1(f ≈1.9447。 3

3．利用 xxf , [ 1 0 , x L p 当而 n 1+= n p ≤ 时，对 j p 时， 1 5 )(3 xN = = ( 4. )(3 xL j 0 p = ] = xf ( ) ∑ j x ( +′ ω n 1 p , ,1,0 L= ， x xf ( ( ) ′= ω n 1 + ，并注意 ) j =jxf ( 3 x − 13 x 2 + 69 x − )92 5. （1）用反插值法得根的近似值 =0.3376； *α 0 ) ，故有，故有 xxf , [ 1 xxf x [ , , 0 L 1 x 1] , , = pL , 0 ] p = 0 p n p ≤ 1 += ， n ) 1 + n （2）用牛顿迭代法得根的近似值 =0.337667。 *α 6. 令 x k max xx ≤≤ − 1 k f )( )3( ξ !3 + 1 ( x − x )( x − x k )( x − x k 1 + ) ≤ 10 − 3 k 1 − 可求得 ≤0.2498（或 ≤0.2289）。 h h 7. (1) xH )( 3 −= 2 x 3 + 8 x 2 − 9 x + 5 xR )( 3 = (2) H 3 x )( = 3 2 x − 9 x 2 + 15 x − 6 xR )( 3 = 1 !4 1 !4 f )4( )( ( ξ x − ()1 2 x − 2 )2 )2,1(∈ξ f )4( )( ( ξ x − )(1 x − ()2 2 x − )3 )3,1(∈ξ 1．正规方程组为 1 ≈x .2 3888 ， 2 ≈x .0 4456    30 3 5 5327 3 49 = 第六章 x 73      1      x 29      2 a 5327       b    4.271   369321 5.  y =    7277699 0500 = .0 9726 + .0 0500 x 2  2．正规方程组为   .0≈a 3．取对数 9726 ln ， b I I = ln 0 .0≈ at − 相应的正规方程组为 5.3 −   03.2  72825 7   5.3 −  ln 0 =I .1 = I 0 ln a 9890 .1     − 1858 .0   .2≈a 8882 ，       0 ≈I .5 6308 I = .5 e 6308 − .2 8882 t 4．正规方程组为 1781 6092 4 1781 .3 .3    .3 4.14 9607 .12 .2≈a 4864 ， .1≈b 4016 y = .2 4864 + .1 4016 ln x           =  a   b  第七章 ∫ )01( e ξ e x − 1 0 1 12 1 ∫ 0 1 1 2 1 12 1. 解：运用梯形公式： dx ≈ 0 [ e + 1 e .1] = 8591409 误差： fR [ ] −= 3 ≤ e = .0 2265235 运用辛浦生公式： e x dx ≈ e ξ ≤ 误差： fR [ ] −= 2880 2. 解：（1）左矩形公式 xf )( 将 f(x)在 a 处展开，得 1 6 0 [ e + e 4 1 2 + 1 e .1] = 7188612 1 2880 e = .0 00094385 = af )( f ( )( ′+ ξ ax − ), ξ ∈ xa ],[ 4

b b a dxaf )( = ∫ dxxf )( 两边在[a,b]上积分，得 ∫ ],[ ba∈η 由于（x-a）在[a,b]上不变号，故有 1 2 afab )( ( dxxfb 从而有 )( ∫ + − = ) f a a + b ∫ a ，使 f b ∫ a ab )( ( ′ η − 2 ) ∈ η ba ],[ )( ( ′ ξ dxax − ) = afab ( )( − ) + dxxf )( = afab ( )( − ) f ′+ )( η b a b ∫ ∫ a f )( ( ′ ξ dxax − ) ( dxax − ) （2）右矩形公式将 f(x)在 b 处展开，并积分，得 dxxfb )( ∫ a = bfab ( )( − ) − 1 2 f ab )( ( ′ η − ) 2 ∈ η ba ],[ （3）中矩形公式将 f(x)在 a + 处展开，得 b 2 baf + ( 2 xbaf )( ( ′+ + 2 ) xf )( = − ba + 2 ) + 1 2 f )( ( ′′ ξ x − ba + 2 ,) 2 ξ ∈ ba ],[ b a = 两边在[a,b]上积分，得 ∫ ( bafab + dxxf )( ( − 2 bafab + )( ( ′′ − η 2 1 2 + = ( ) ) ) ) f ) baf + ( ′+ 2 ba + 2 ∫ − x ( b a b a ∫ ) ( x − 2 dx = b + dxba 1 + ∫ f ) 2 2 bafab + ( − 2 ( ) a ) dx − 2 ) ba + 2 ab ( )( ′′ η − ,) 3 η ∈ ba ],[ )( ( ′′ ξ x + 1 24 f 2 3 1 1 3 4 3 3 h h − − 1 − 1 ( ) ) ( h h + = A A A h = − + = = dx x h A − 解得 + 1 − Ah ( 2 0 h 2 3 A + 0 1 ) A − A-1=A1=h/3, A0=4h/3 h 3 h 3 dxxf )( 3. 解：（1）求积公式中含有三个待定参数 A-1、A0、A1，故令求积公式对 f(x)=1、x、x2 准确成立，即         显然所求的求积公式（事实上为辛浦生公式）至少具有两次代数精确度。又有 ∫ ∫ 故 ∫− （2）求积公式中含有两个待定参数 x1、x2，当 f(x)=1 时，有 1 ∫− 故令求积公式对 x、x2 准确成立，即： 2   2  hh 3 hh 3 h ( +− 具有三次代数精确度。 ) + fh 3 xf (2)1( +− 1 hfh )( 3 68990 .0 .0 52660 fh 4 3 xf (3) + .0   −  −  .0  dxxf )( 28990 12660 解得， x 1 x 1 )0( 1 3 x h dx x 1 )] = = + − ≠ ≈ ≡ h x ( [ ) f − h h 4 4 2 1 2 x 3 + 2 2 x 3 + 1 ∫ x 1 − 3 dx 2 = 2 1 1 = 1 3 dxxf )( ≠ 故 1 ∫ 1 − 显然 21[ +− 3 x 1 + 3 x 3 ] 2 ≈ 1 3 [ f xf (2)1( +− 1 xf (3) + )] 2 当求积节点取 x1=0.68990，x2=-0.12660 或 x1=-0.28990，x2=0.52660 时，求积公式具有两次代数精确度。 5

0 h ≡ dx ++ 0]11[ （3）求积公式中含有一个待定参数α，当 f(x)=1、x 时，有 ∫ ∫ 故令求积公式对 f(x)=x2 成立，即： h 2 h 2 ]11[ xdx h α 0[ h α xh dx 0[ − + + ≡ + + = h h ] ] h 0 2 2 2 h 2 2 h ]202[ −× ∫ 0 2 ] α=1/12。显然： dx h 30[ 0[ h − + + ] 3 得 h ∫ 0 h ∫ 0 x x 故 ∫ 0 3 = h 2 h 2 dxxfh )( dx ≠ 4 0[ ≈ 4 h + fh [ 2 h 2 12 h 2 12 ] + ]40[ 3 − h )0( + hf ( )] + h 2 12 [ f )0( ′ hf ( ′− )] 具有三次代数精确度。 4. 解：函数值表格 x f(x) 1 0 7/6 8/6 9/6 10/6 11/6 2 0.15415 0.28768 0.40547 0.51083 0.60614 0.69315 T6=1/2×1/6[0+2×(0.15415+0.28768+0.40547+0.51083+0.60614)+0.69315]≈0.38514 S3=1/6×1/3[0+4×(0.15415+0.40547+0.60614)+2×(0.28768+0.51083)+0.69315]≈0.38629 fRN ][ −= 5. 解： xf )( = Q 令 ×≤fRN ] [ 1 2 4 fhab − 2880 x , ln ∴ )4( f )4( x )( )( η 1 −= N 2880 ,6 f )4( ∴−= x 4 4 f )4( ), ( η 1 ≤≤ η 2 )( η ≤ .6 410 − ，得 N≥2.54.取 N=3,则至少要取 2N+1=7 个节点处的函数值。 6. 解：按照事后误差估计公式 I T ( ), T T T + ≈ − 2 n 2 n n 2 n 1 3 = 1 2 T n + ( S 2 n − S ), n S n = I S ≈ 和 1 15 计算列表如下： + n 2 h n 2 4 3 1 n ∑− = 0 k xf ( k + 1 2 T 2 n − 1 3 T n ) k 等分 2k 1 2 4 8 kT 2 1 3 T k 2 − T k − 1 2 12 −kS 1 15 S k 2 − − 1 S k − 2 2 0.92073549 0.93979328 0.94451352 0.94569086 0 1 2 3 因此，由梯形公式得 I≈T8=0.94569086,精确到 10-3；由辛浦生公式得到 I≈S2=0.94608693，精确到 10-5。若取 I≈S4=0.94608331，则精确到 10-6。精确到 10-3 的结果为 I≈0.946. 0.94614588 0.94608693 0.94608331 0.00000393<10-5 0.00039245<10-3 0.00157341 0.00000024 6

7. 解：采用极坐标系，令 x=2cosθ，y=sinθ，则椭圆的周长为由于 π 2 0 ∫ sin31 + l 4 = π π < ∫ 2 2 0 x dy 2 2 ′+′ θ θ θ = 2 d θθ ×< 2 差≤1/2×10-3。列表计算如下： k 等分 2k kT2 0 1 2 3 4 1 2 4 8 16 2．356194 2．419921 2．422103 2．422112 2．422112 π ∫ 4 2 0 π 2 = sin31 + 2 θθ d = 4 I π ，因此 I 有一个整数，故要求结果有四位有效数字，需截断误 12 −kS 2．441163 2．422830 2．422115 2．422112 2 −kC 2 2 −kR 3 2．421608 2．422067 2．422112 2．422074 2．422113 故取 I=2.422113，周长为 l =4I=9.688。 ,9.1 8.（1）：取 h=0.1，三点公式取 x = 0 = ,0.2 x 2 = 1.2 ，得 f )1.2( − f )]9.1( = .22 )9.1( − )0.2(2 f + f )]1.2( = .29 5932 x 1 2288 x 1 4142 f f )0.2( ′ ≈ )0.2( ′′ ≈ [ 1 1.02 × 1 f [ 1.0 2 f f ≈ ≈ )0.2( ′ )0.2( ′′ 1 2.02 × 1 f [ 2.0 注：精确解为第八章 1. 计算结果为： f 2 （2）：取 h=0.2，三点公式取 x 0 = ,8.1 = ,0.2 x 2 = 2.2 ，得 [ f )2.2( − f )]8.1( = .22 )8.1( − )0.2(2 f + f )]2.2( = .29 7043 )0.2( ′ = .22 167168 , f )0.2( ′′ = .29 556224 。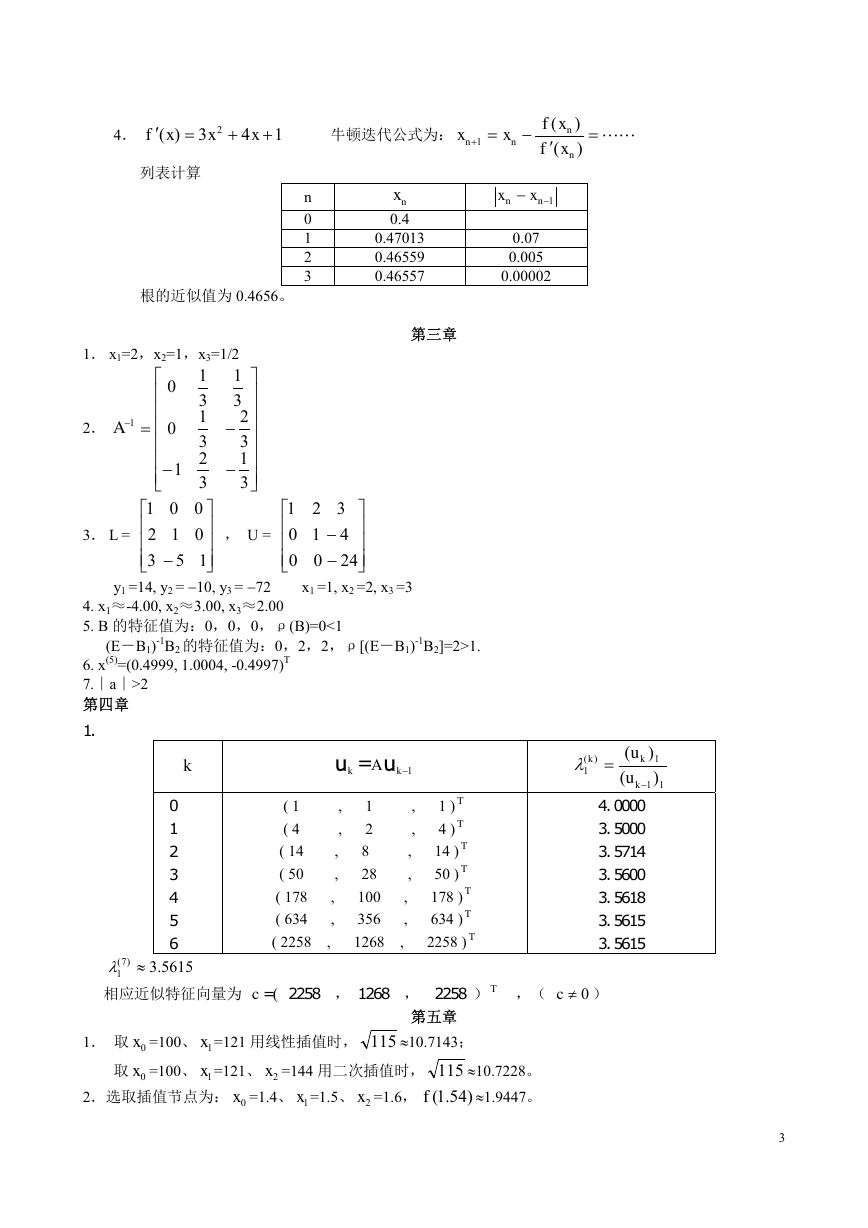 nx 1.0 2.0 3.0 ny 000 000 .0 000 .0 011 000 000 .0 033 900 000 | xy ( n ) − y n | 516.0 258 196 × 210 − 102.0 692 469 × 110 − 152.0 817 793 × 110 − 2. 计算结果如下： nx 0.1 0.2 0.3 .1 .1 .0 3. 计算结果如下：梯形法 ny 618 818 269 488 490 947 181 421 708 y − n 934 xy |) ( | n 310 878 548. − × 310 898558403 . − × 210 110. 620 − × 314 欧拉预-校法 ny 620 .1 .1 272 951 .0 000 000 000 000 400 368 | 126. 207. 255. y − n 924 995 636 xy ( 692 396 391 |) n 210 − × 210 − × 210 − × 7

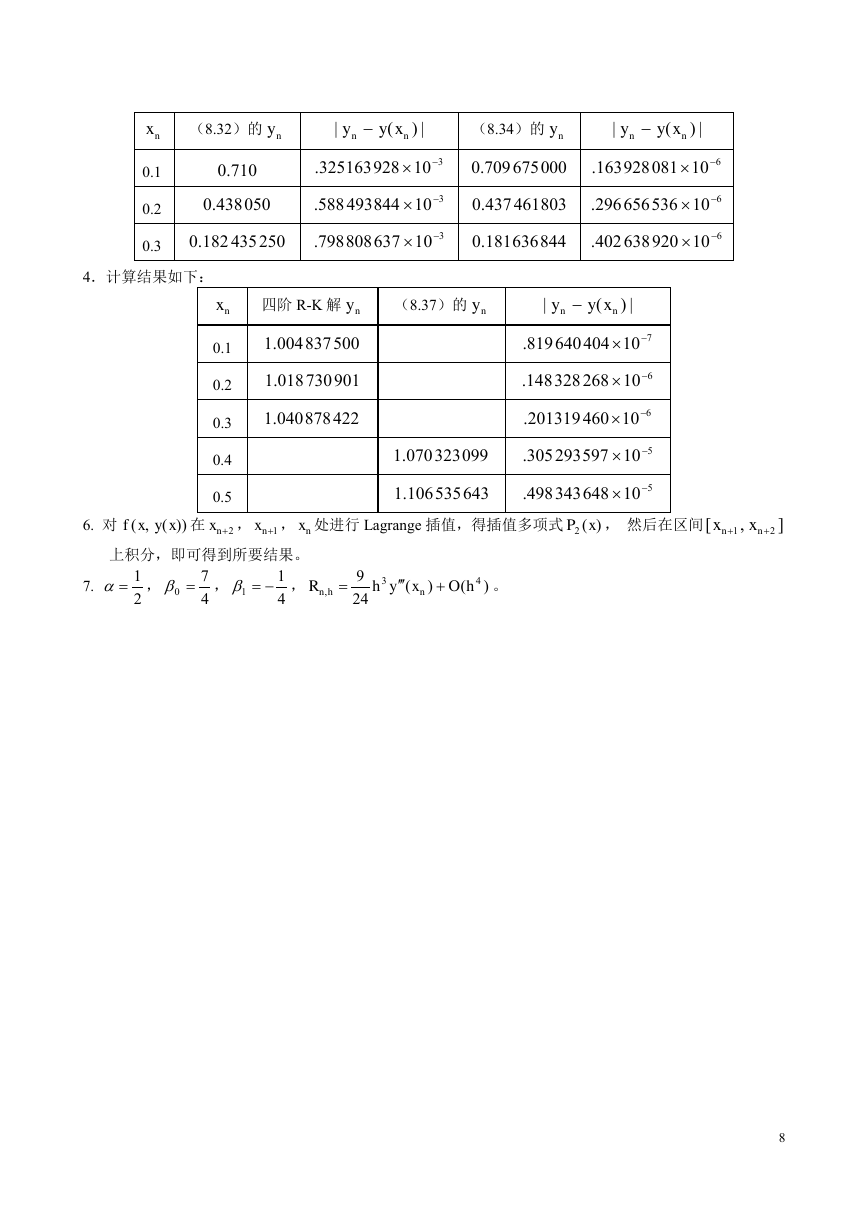
nx （8.32）的 ny | y − n xy ( n |) 710 325. 163 928 × 310 − （8.34）的 ny .0 709 000 675 | y − n xy ( n | ) 163. 928 081 × 610 − 050 588. 493 844 × 310 − .0 437 461 803 296. 656 536 × 610 − .0 182 435 250 798. 808 637 × 310 − .0 181 636 844 402. 638 920 × 610 − .0 438 .0 0.1 0.2 0.3 4．计算结果如下： nx 四阶 R-K 解 ny （8.37）的 ny | y − n xy ( n |) 0.1 0.2 0.3 0.4 .1 004 837 500 .1 018 730 901 .1 040 878 422 323 .1 070 819. 640 404 × 710 − 148. 328 268 × 610 − 201. 319 460 × 610 − 099 305. 293 597 × 510 − 498. 在，，处进行 Lagrange 插值，得插值多项式 643 535 106 .1 0.5 2+nx 648 343 )(2 xP 510 − × ，然后在区间[ 6. 对 )) 1+nx xyxf ,( ( nx 上积分，即可得到所要结果。 R −=β =α ，，， 0 =β 1 1 2 7 4 1 4 = hn , 9 24 3 yh ( ′′′ x n ) + hO ( 4 ) 。 7. x n 1 + , x n + 2 ] 8

资料库

西北工业大学计算方法习题答案.pdf

相关推荐

课程资源

热门标签

最新资料