logo资料库

实验三-PCM编码译码.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.51M 资料格式：doc 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    实验三 PCM 编码译码仿真 学院（院、系） 专业 班 通信原理 课程 学号 姓名 实验日期 教师评定 一、实验目的 1．熟悉 PCM（脉冲编码调制）原理。 2．掌握编写 PCM（脉冲编码调制）程序的要点。 3．掌握使用 Matlab 调制仿真的要点。 二、实验内容 1．根据 PCM（脉冲编码调制）原理，设计源程序代码。 2．通过 Matlab 软件仿真给定模拟信号编码后的波形。 3. 对比给的原始信号波形和译码后的波形。 三、实验原理 1.脉冲编码调制 脉冲编码调制在通信系统中是一种对模拟信号数字化的取样技术，将模拟信号变换 为数字信号的编码方式。 PCM 的实现主要包括三个步骤完成：抽样、量化、编码。分 别完成时间上离散、幅度上离散、及量化信号的二进制表示。根据 CCITT 的建议，为 改善小信号量化性能，采用压扩非均匀量化，有两种建议方式，分别为 A 律和律方 式，本设计采用了 A 律方式。由于 A 律压缩实现复杂，常使用 13 折线法编码，采用非 均匀量化 PCM 编码示意图如图 1 所示 图1 PCM编码示意图 第 1 页 共 10 页
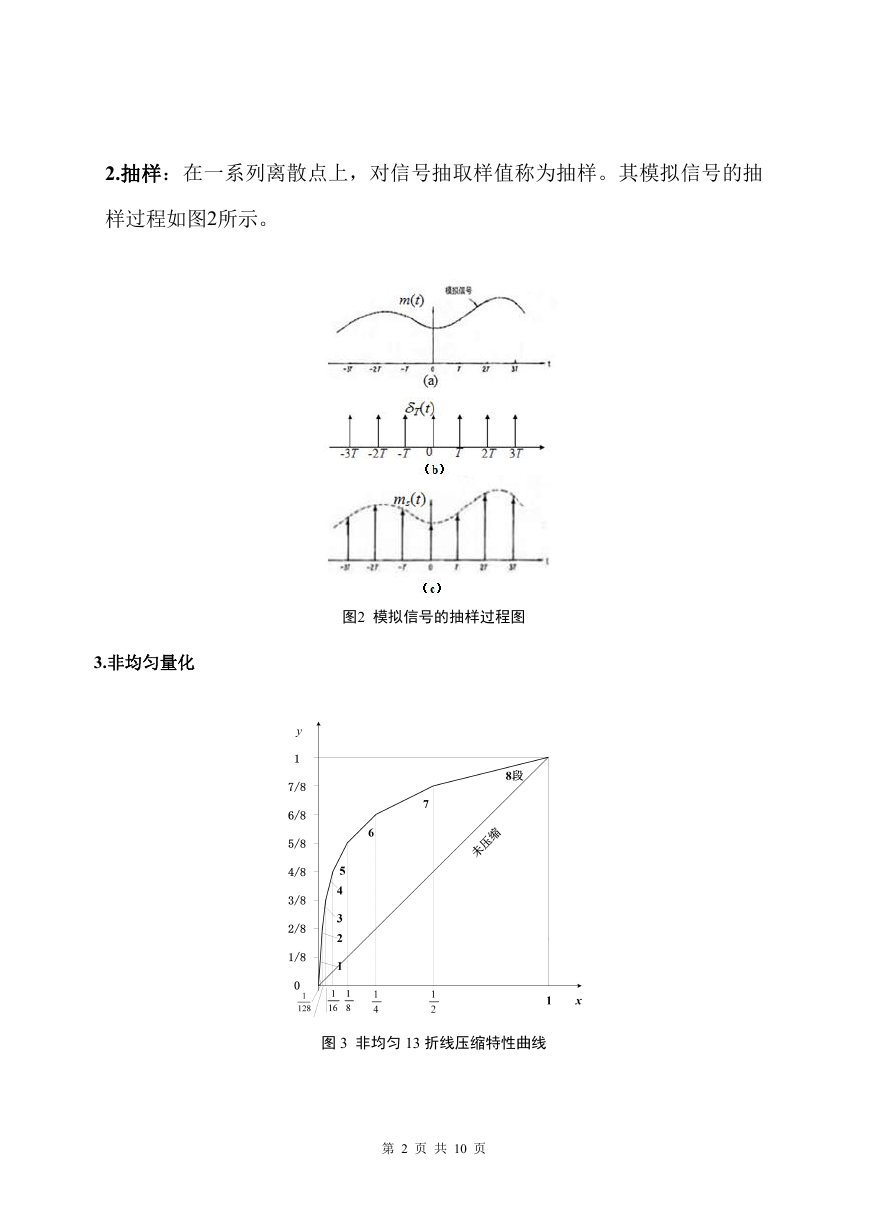
    2.抽样：在一系列离散点上，对信号抽取样值称为抽样。其模拟信号的抽 样过程如图2所示。 图2 模拟信号的抽样过程图 3.非均匀量化 图 3 非均匀 13 折线压缩特性曲线 第 2 页 共 10 页
    图 4 非均匀 13 折线编码原理图 在实际应用中，量化器设计好后，量化电平数M和量化间隔  都是确定的。量化 噪声Nq 也是确定的。但是，信号的强度会影响信号量噪比，当信号小时，信号量噪比 也就越小。因此，均匀量化器对小输入信号很不利，为了克服这个缺点，以改善小信号 时的信号量噪比，采用下述的非均匀量化方式。 在非均匀量化中，量化间隔是随信号抽样值的不同而变化的。信号抽样值小时，量 化间隔  也小；信号抽样值大时，量化间隔  也大，非均匀量化的实现方法有两种： 一种是北美和日本采用的μ律压扩，一种是欧洲和我国采用的 A 律压扩，常采用的近似 算法是 13 折线法，该算法的压缩特性图如图 3 所示。 信号小时，Δ小，信号大时，Δ大。一般语音信号，信号幅度小出现的概率大，信 号幅度大出现的概率小。通过非均匀量化，使得平均信噪比增大。 13 折线 A 律 PCM 的非线性编码方法具体过程如表 1 所示。 在 13 折线法中采用的折叠码有 8 位。其中一位 c1 表示量化值的极性正负，后 7 位 分为段落码和段内码两部分。用于表示量化值的绝对值。其中第 2~4 位（c2~c4）是段 落码，5~8 位（c5~c8）为段内码，可以表示每一段落内的 16 种量化电平。段内码代表 的 16 个量化电平是均匀分布的，因此，这 7 位码总共能表示 27=128 种量化值。编码方 法如下所示： 极性码 段落码 段内码 C1 C2C3C4 C5C6C7C8 （1）将量化区间［a,b］分为 4096 个小段 （2）正半轴 2048 个小段，负半轴 2048 个小段 （3）每个小段用Δ表示 第 3 页 共 10 页
    表 1 非均匀 13 折线编码原理 四、程序设计 1. 首先给定一个模拟信号。 2. 根据 PCM（脉冲编码调制）原理，对模拟信号进行抽样，得到离散信号， 然 后进行非均匀量化编码 ，采用 13 折线法。 3. 在 Matlab 当中进行操作时，首先要画出经过 PCM 调制的模拟信号波形。 4. 将经过 PCM 调制的信号叠加上一个高斯白噪声信道，然后，根据非均匀量化译 第 4 页 共 10 页
    码原理，得到译码后的波形，即原始的模拟信号。 五、设计流程 1. 输入一个模拟信号，根据奈奎斯特定理，进行抽样，得到时间上离散的模拟信 号。 2. 根据非均匀量化编码（13 折线法），设定模拟信号各个段的段落码和段内码。 并画出量化编码后的波形。 3. 根据非均匀量化编码（13 折线法）的逆向思想，即不同的段落码和段内码分别 对应不同的电平值，最终得到译码后的模拟信号，然后画出译码后的模拟信号的波形。 六、源程序代码 T=0.002; t=-0.1:T:0.1; xt=cos(2*pi*30*t)+sin(2*pi*65*t); fs=500; sdt=1/fs; t1=-0.1:sdt:0.1; st=cos(2*pi*30*t)+sin(2*pi*65*t); figure(1); subplot(3,1,1); plot(t,xt);title('原始信号'); grid on subplot(3,1,2); stem(t1,st,'.');title('量化信号'); title('抽样信号'); grid on n=length(st); M=max(st); C=(st/M)*2048; 第 5 页 共 10 页
    code=zeros(1,8); for i=1:n if C(i)>=0 code(i,1)=1 code(i,1)=0 else end if abs(C(i))>=0&&abs(C(i))<16 code(i,2)=0;code(i,3)=0;code(i,4)=0;step=1;start=0; elseif 16<=abs(C(i))&&abs(C(i))<32 code(i,2)=0;code(i,3)=0;code(i,4)=1;step=1;start=16; elseif 32<=abs(C(i))&&abs(C(i))<64 code(i,2)=0;code(i,3)=1;code(i,4)=0;step=2;start=32; elseif 64<=abs(C(i))&&abs(C(i))<128 code(i,2)=0;code(i,3)=1;code(i,4)=1;step=4;start=64; elseif 128<=abs(C(i))&&abs(C(i))<256 code(i,2)=1;code(i,3)=0;code(i,4)=0;step=8;start=128; elseif 256<=abs(C(i))&&abs(C(i))<512 code(i,2)=1;code(i,3)=0;code(i,4)=1;step=16;start=256; elseif 512<=abs(C(i))&&abs(C(i))<1024 code(i,2)=1;code(i,3)=1;code(i,4)=0;step=32;start=512; elseif 1024<=abs(C(i))&&abs(C(i))<2048 code(i,2)=1;code(i,3)=1;code(i,4)=1;step=64;start=1024; end B=floor((abs(C(i))-start)/step); t=dec2bin(B,4)-48; code(i,5:8)=t(1:4); end code=reshape(code',1,8*n); 第 6 页 共 10 页
    subplot(3,1,3);stem(code,'.');axis([1 64 0 1]); title('编码信号'); grid on y=awgn(code,5); figure(2); stem(y,'.');axis([1 64 0 3]); title('叠加加性高斯信号的信号'); n=length(code); code=reshape(code',8,n/8)'; slot(1)=0;slot(2)=32; slot(3)=64;slot(4)=128; slot(5)=256;slot(6)=512; slot(7)=1024;slot(8)=2048; step(1)=2;step(2)=2;step(3)=4;step(4)=8; step(5)=16;step(6)=32;step(7)=64;step(8)=128; for i=1:n/8 ss=2*code(i,1)-1; tmp=code(i,2)*4+code(i,3)*2+code(i,4)+1; st=slot(tmp); dt=(code(i,5)*8+code(i,6)*4+code(i,7)*2+code(i,8))*step(tmp)+0.5*step(tmp); v=1; r(i)=ss*(st+dt)/4096*v; end T=0.002; t=-0.1:T:0.1; figure(3); subplot(1,1,1); 第 7 页 共 10 页
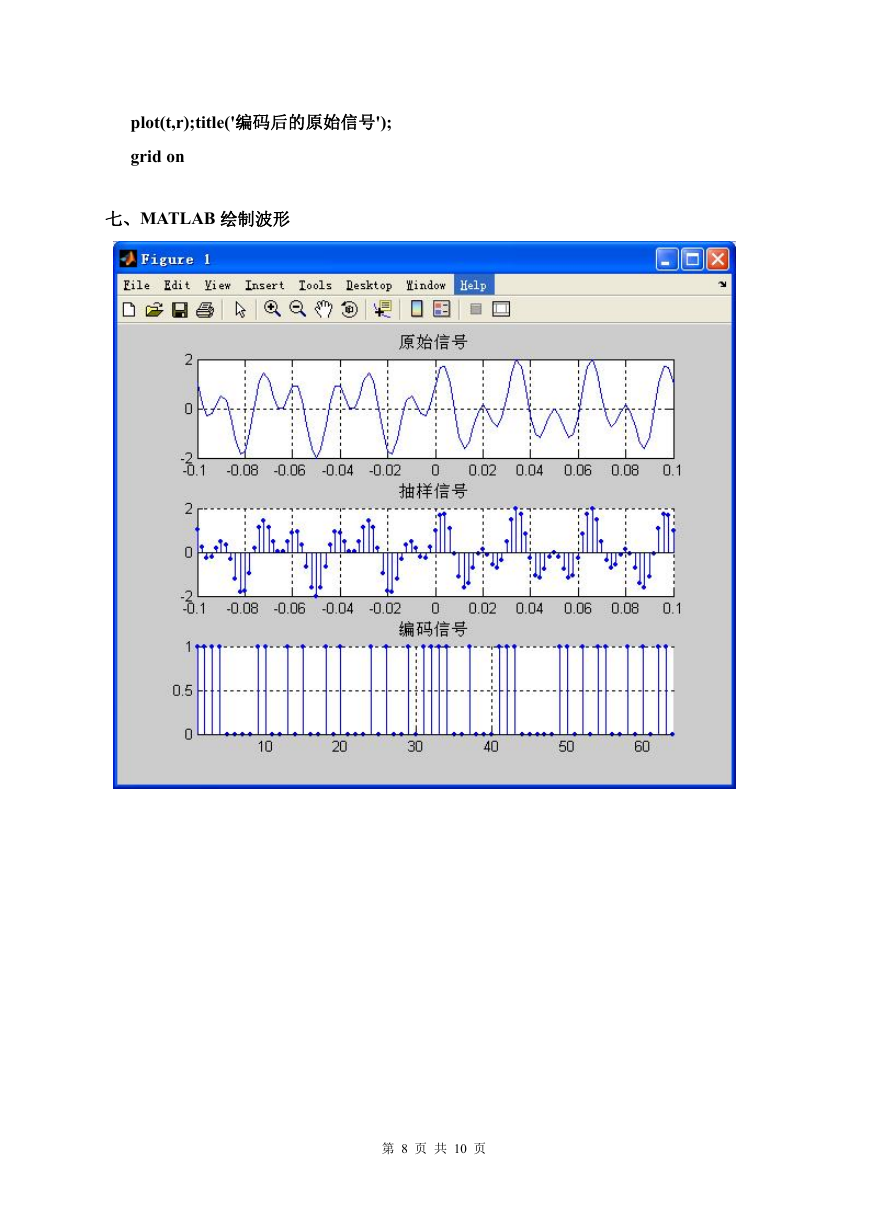
    plot(t,r);title('编码后的原始信号'); grid on 七、MATLAB 绘制波形 第 8 页 共 10 页
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料