logo资料库

矩阵低秩分解理论.ppt

发布时间：2022-06-19 发布人：admin 分类：说明书 资料大小：6.98M 资料格式：ppt 举报 版权申诉
第1页 / 共38页
第2页 / 共38页
第3页 / 共38页
第4页 / 共38页
第5页 / 共38页
第6页 / 共38页
第7页 / 共38页
第8页 / 共38页
资料共38页，剩余部分请下载后查看
    矩阵低秩分解理论及其应用分析 成科扬 2013年9月4日
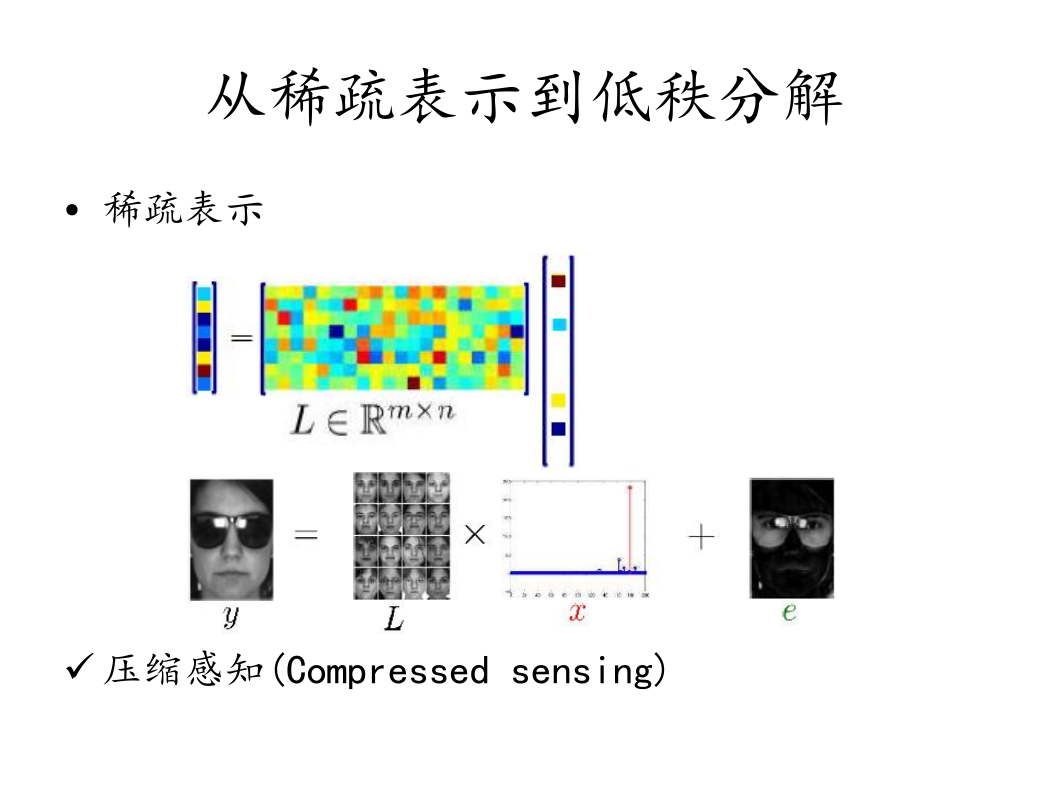
    从稀疏表示到低秩分解 • 稀疏表示 ü 压缩感知(Compressed sensing)
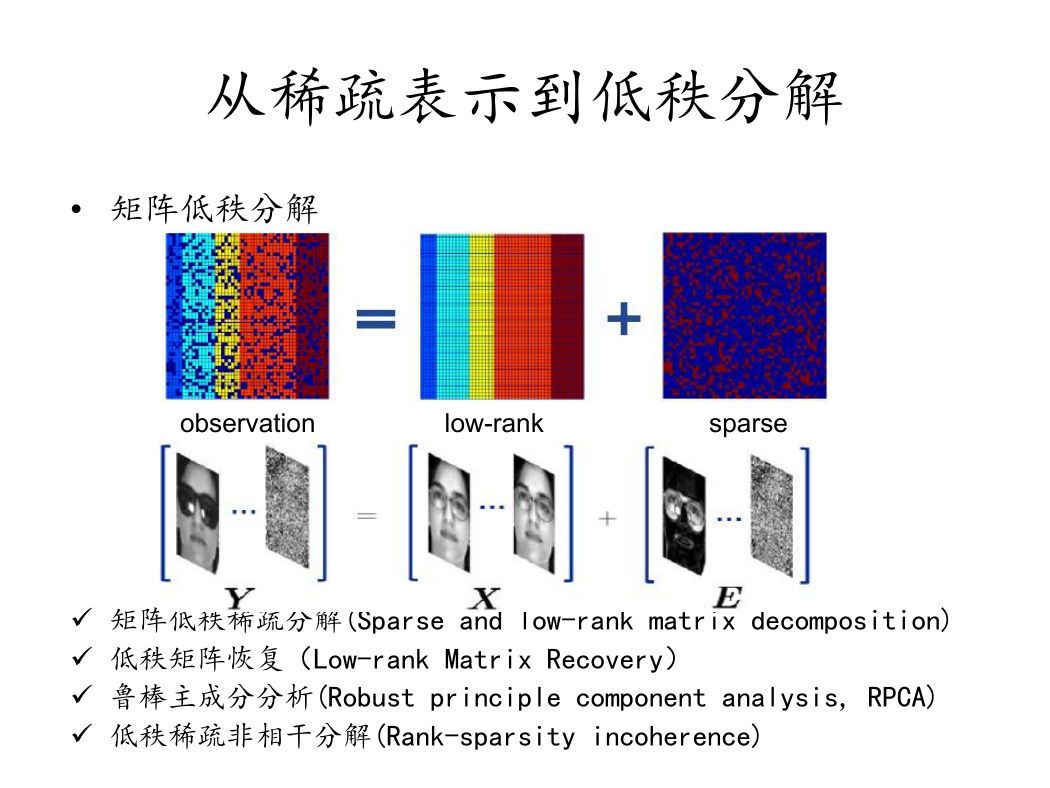
    从稀疏表示到低秩分解 • 矩阵低秩分解 observation low-rank sparse ü 矩阵低秩稀疏分解(Sparse and low-rank matrix decomposition) ü 低秩矩阵恢复（Low-rank Matrix Recovery） ü 鲁棒主成分分析(Robust principle component analysis, RPCA) ü 低秩稀疏非相干分解(Rank-sparsity incoherence)
    预备知识
    低秩矩阵恢复（鲁棒主成分分析RPCA） • 在许多实际应用中，给定的数据矩阵Ｄ往往是低秩或近似低 秩的，但存在随机幅值任意大但是分布稀疏的误差破坏了原 有数据的低秩性，为了恢复矩阵Ｄ的低秩结构，可将矩阵Ｄ 分解为两个矩阵之和，即Ｄ＝Ａ＋Ｅ，其中矩阵Ａ和Ｅ未知， 但Ａ是低秩的。当矩阵Ｅ的元素服从独立同分布的高斯分布 时，可用经典的PCA来获得最优的矩阵Ａ，即求解下列最优 化问题： 当Ｅ为稀疏的大噪声矩阵时，问题转化为双目标优化问题： 引入折中因子λ，将双目标优化问题转换为单目标优化问题：
    RPCA的求解 • 凸松弛 矩阵核范数 NP难问题 松弛后
    迭代阈值算法（iterative thresholding，IT） 将最优化问题正则化，便得到优化问题： 优化问题式的拉格朗日函数为 使用迭代阈值算法交替更新矩阵Ａ,Ｅ和Ｙ。当Ｅ=Ｅk，Ｙ=Ｙk时， 当Ａ＝Ａk+1，Ｙ＝Ｙk时， 当Ａ＝Ａk+1 ，Ｅ＝Ｅk+1时， 其中：步长δk满足０＜ δk ＜1 • ＩＴ算法的迭代式形式简单且收敛，但它的收敛速度比较慢，且难以选取合适的步长
    加速近端梯度算法（accelerated proximal gradient， APG） • 将优化问题式的等式约束松弛到目标函数中，得到如下的拉格朗日函 数： 记 • 于是L(Ａ,Ｅ,μ)=ｇ(Ａ,Ｅ,μ)+ｆ(Ａ,Ｅ)。函数ｇ(Ａ,Ｅ,μ)不可微，而ｆ (Ａ,Ｅ)光滑且具有李普希兹连续梯度，即存在Lf＞0，使得 其中： 表示函数ｆ(Ａ,Ｅ)关于矩阵变量Ａ和Ｅ的Ｆｒéｃｈｅ ｔ梯度。此处取Lf =２。对于给定的与Ｄ同型的两个矩阵ＹA和ＹE，作 Ｌ(Ａ,Ｅ,μ)的部分二次逼近：
    分享到：
    赞 收藏

    相关推荐

    资料库

    人工智能

    共收录2047份资料，累计62个分类，关注成员有19位，主要包括：GNSS,Pico-SIM868-GSM,GPRS,NB-IoT,GPRSHAT,SIM7070GCat-M,GNSSHAT,GSM,NB-IoTHAT,SIM7080GCat-M,R800CGSM,SIM800CGSM,UPSPowerModule(B),UPSPowerModule,Pico-SIM7020C-NB-IoT,SIM7028NB-IoTHAT,SIM7020CNB-IoTHAT,SIM7000XNB-IoTHAT,A7670CCat-1HAT,A7600C1Cat-1,SIM7600X4G&LTECat-1HAT,SIM7600X4GDONGLE用户手册,RM520N-GL5GHAT,RM500Q-GL5GHAT,RM500U-CN5GHAT,SIM820X-M25GforJetsonNano,AudioCardforJetsonNano,SIM7600G-H4GforJetsonNano,OpenNCC-Lite-4G8M,IMX219-77Camera,13.3inche-PaperHAT,10.3inche-PaperHAT(D),10.3inche-PaperHAT,9.7inche-PaperHAT,7.8inche-PaperHAT,6inchHDTouche-PaperHAT,6inchHDe-PaperHAT,6inche-PaperHAT,5.83inche-PaperHAT(C),LCD-Clock-A,0.95inchRGBOLED(A),0.96inchRGBOLEDModule,0.96inchOLEDModule,0.96inchOLED(A),1.27inchRGBOLEDModule,1.3inchOLEDModule(C),1.3inchOLED(A),1.32inchOLEDModule,1.5inchRGBOLEDModule,1.5inchOLEDModule,JETSONORINNX,自然语言处理,搜索引擎,VR,计算广告,深度学习,机器学习

    热门标签

    GNSS Pico-SIM868-GSM GPRS NB-IoT GPRSHAT SIM7070GCat-M GNSSHAT GSM NB-IoTHAT SIM7080GCat-M R800CGSM SIM800CGSM UPSPowerModule(B) UPSPowerModule Pico-SIM7020C-NB-IoT SIM7028NB-IoTHAT SIM7020CNB-IoTHAT SIM7000XNB-IoTHAT A7670CCat-1HAT A7600C1Cat-1 SIM7600X4G&LTECat-1HAT SIM7600X4GDONGLE用户手册 RM520N-GL5GHAT RM500Q-GL5GHAT RM500U-CN5GHAT SIM820X-M25GforJetsonNano AudioCardforJetsonNano SIM7600G-H4GforJetsonNano OpenNCC-Lite-4G8M IMX219-77Camera 13.3inche-PaperHAT 10.3inche-PaperHAT(D) 10.3inche-PaperHAT 9.7inche-PaperHAT 7.8inche-PaperHAT 6inchHDTouche-PaperHAT 6inchHDe-PaperHAT 6inche-PaperHAT 5.83inche-PaperHAT(C) LCD-Clock-A 0.95inchRGBOLED(A) 0.96inchRGBOLEDModule 0.96inchOLEDModule 0.96inchOLED(A) 1.27inchRGBOLEDModule 1.3inchOLEDModule(C) 1.3inchOLED(A) 1.32inchOLEDModule 1.5inchRGBOLEDModule 1.5inchOLEDModule JETSONORINNX 自然语言处理 搜索引擎 VR 计算广告 深度学习 机器学习

    最新资料