计算机图形学图形变换.doc

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：0.10M 资料格式：doc 举报版权申诉

xiaocuivw-3970435-16359647309338955694.doc.pdf-第1页.png

第1页 / 共7页

xiaocuivw-3970435-16359647309338955694.doc.pdf-第2页.png

第2页 / 共7页

xiaocuivw-3970435-16359647309338955694.doc.pdf-第3页.png

第3页 / 共7页

xiaocuivw-3970435-16359647309338955694.doc.pdf-第4页.png

第4页 / 共7页

xiaocuivw-3970435-16359647309338955694.doc.pdf-第5页.png

第5页 / 共7页

xiaocuivw-3970435-16359647309338955694.doc.pdf-第6页.png

第6页 / 共7页

xiaocuivw-3970435-16359647309338955694.doc.pdf-第7页.png

第7页 / 共7页

文本预览

计算机图形学学生姓名：专业学号：完成日期：

实验题目：图形变换实验目的：通过实验掌握三维直线的几何变换，窗口的裁剪以及视区的变换。实验内容：1.定义三维直线，进行几何变换（如平移，投影变换） 2.窗口进行裁剪（算法自选） 3.窗口视区变换并显示（裁剪前，裁剪后截图） 4.程序要有注释实验原理：一直线的平移：平移变换是将平面上的一点（x,y）沿平行于 x 轴的方向平移，沿平行于 y 轴的方移后变成点 ( x y ,  ) , x    ， x T x y    y T y 二投影投影平面与投影方向垂直的投影称为正交投影。一种常见的正交投影是等轴投影，即投影平面与三个坐标轴的夹角都相等。为了显示等轴投影，一般构造空间中的一个正方体，它可以由它的八个顶点来表示。将这八个顶点分别利用投影矩阵投影到二维平面上，再将原来具有邻接关系的顶点连接起来就得到了三维图形投影之后的二维图形。三窗口裁剪在定义了窗口之后，只需将窗口内的图形显示出来，对于窗口之外的图形一般是不关心的。因此，必须将窗口外的图形裁剪下去。对直线段进行裁剪的算法有 Cohen-Sutherland 算法、中点分割算法、梁友栋-Barsky 算法，并且利用 Sutherland-Hodgman 算法实现对多边形的裁剪。本实验采用 LiangBarsk 算法。四窗口视区变换从窗口到视口的映射世界窗口用其左、上、右和下边界描述，分别是 W.l,W.t,W.r 和 W.b。视口在屏幕窗口坐标系中描述，使用 V.l,V.t,V.r,V.b，单位是像素。窗口到视口的映射是基于一个公式生成的，这个公式在世界窗口中对每个给定的点(x, y)都在窗口坐标系中生成一个点(sx, sy)。由于窗口映射到视口是 “成比例”的，而“成比例”这样的要求迫使这种映射具有线性形式。sx = Ax + C ； sy = By + D。四程序及相关截图 1 直线的平移 int pts2[2][4]={{0,0,0,1},{0,0,0,1}};//定义直线 pDC->MoveTo (pts[0][0],pts[0][1]); pDC->LineTo (pts[1][0],pts[1][1]); pDC->MoveTo (pts[0][0]+100,pts[0][1]+100); //直线的平移 x 轴，y 轴各平移 100 pDC->LineTo (pts[1][0]+100,pts[1][1]+100);

2 正等轴测投影变换 int pts[4][4]={{0,0,0,1},{300,0,0,1},{0,100,0,1},{0,0,130,1}}；//重新绘制制直线 int pts2[4][4]={{0,0,0,1},{0,0,0,1},{0,0,0,1},{0,0,0,1}}; for(int i=0;i<4;i++) { pts2[i][0]=pts[i][0]*0.707-pts[i][1]*0.707+200; pts2[i][2]=-pts[i][0]*0.408-pts[i][1]*0.408+pts[i][2]*0.816+200; }//利用正等轴测投影变换公式进行变换 //平移后的直线 pDC->MoveTo (pts2[0][0],pts2[0][2]); pDC->LineTo (pts2[1][0],pts2[1][2]); pDC->LineTo (pts2[2][0],pts2[2][2]); pDC->LineTo (pts2[3][0],pts2[3][2]); pDC->LineTo (pts2[0][0],pts2[0][2]); pDC->LineTo (pts2[2][0],pts2[2][2]); pDC->MoveTo (pts2[1][0],pts2[1][2]); pDC->LineTo (pts2[3][0],pts2[3][2]);

3 窗口的裁剪 void CGty1View::Oncj() { // TODO: Add your command handler code here RedrawWindow(); CDC *pDC=GetDC(); int L[2][4]={{100,100,100,1},{200,200,200,1}};//定义直线 int xl=130,xr=200,yb=100,yt=190,x1,x2,y1,y2;//裁剪边界 CRect rect(xl,yb,xr,yt); CBrush brush(RGB(0,0,255)); pDC->FrameRect(&rect,&brush); //绘制颜色 CPen *pOld,pen(PS_SOLID,1,RGB(255,0,0)); //绘制画笔 pOld=pDC->SelectObject(&pen); x1=L[0][0];y1=L[0][2];x2=L[1][0];y2=L[1][2]; Clip(x1,y1,x2,y2,xl,xr,yb,yt,pDC);//裁剪主函数 }

x=x1+u1*dx;y=y1+u1*dy;、 void CGty1View::Clip(int x1,int y1,int x2,int y2,int xl,int xr,int yb,int yt,CDC *pDC) { float u1=0.0,u2=1.0,dx=x2-x1,dy=y2-y1; float x,y; if(Cliptest(-dx,x1-xl,&u1,&u2))//裁剪左边界 if(Cliptest(dx,xr-x1,&u1,&u2))//裁剪有边界 if(Cliptest(-dy,y1-yb,&u1,&u2))//裁剪下边界 if(Cliptest(dy,yt-y1,&u1,&u2))//裁剪上边界 { if(u1<=u2)//如果直线在窗口内 { x2=x1+u2*dx;y2=y1+u2*dy;//计算可见端点 x1=x;y1=y; pDC->MoveTo(x1,y1); pDC->LineTo(x2,y2); } } } //对一条边界进行裁剪 int CGty1View::Cliptest(float p,float q,float *u1,float *u2) { float r; int re=1; if(p<0.0)//直线从边界外部延伸到窗口内 { r=q/p; *u1=(*u1>r)?*u1:r; } else if(p>0.0)？//直线从窗口内部延伸到外部 { r=q/p; *u2=(*u2

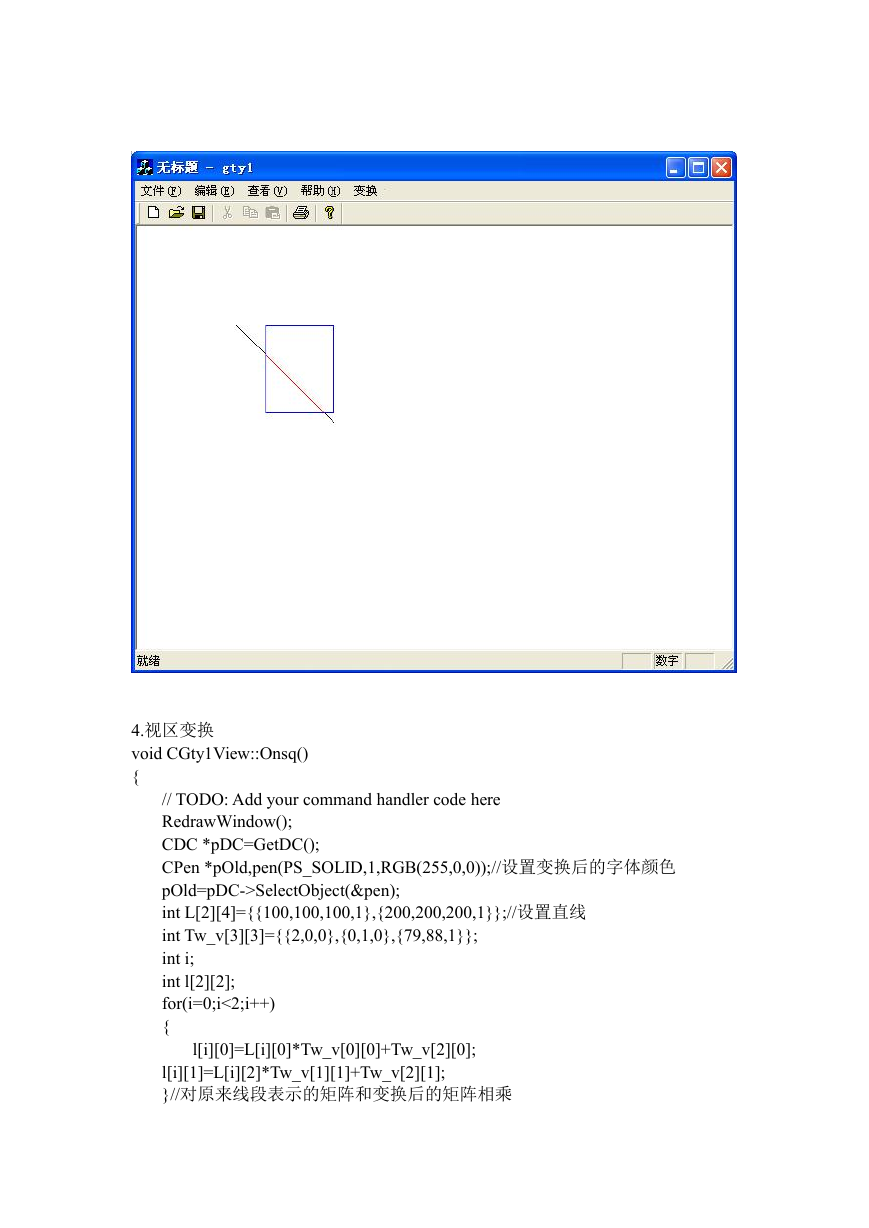
4.视区变换 void CGty1View::Onsq() { // TODO: Add your command handler code here RedrawWindow(); CDC *pDC=GetDC(); CPen *pOld,pen(PS_SOLID,1,RGB(255,0,0));//设置变换后的字体颜色 pOld=pDC->SelectObject(&pen); int L[2][4]={{100,100,100,1},{200,200,200,1}};//设置直线 int Tw_v[3][3]={{2,0,0},{0,1,0},{79,88,1}}; int i; int l[2][2]; for(i=0;i<2;i++) { l[i][0]=L[i][0]*Tw_v[0][0]+Tw_v[2][0]; l[i][1]=L[i][2]*Tw_v[1][1]+Tw_v[2][1]; }//对原来线段表示的矩阵和变换后的矩阵相乘

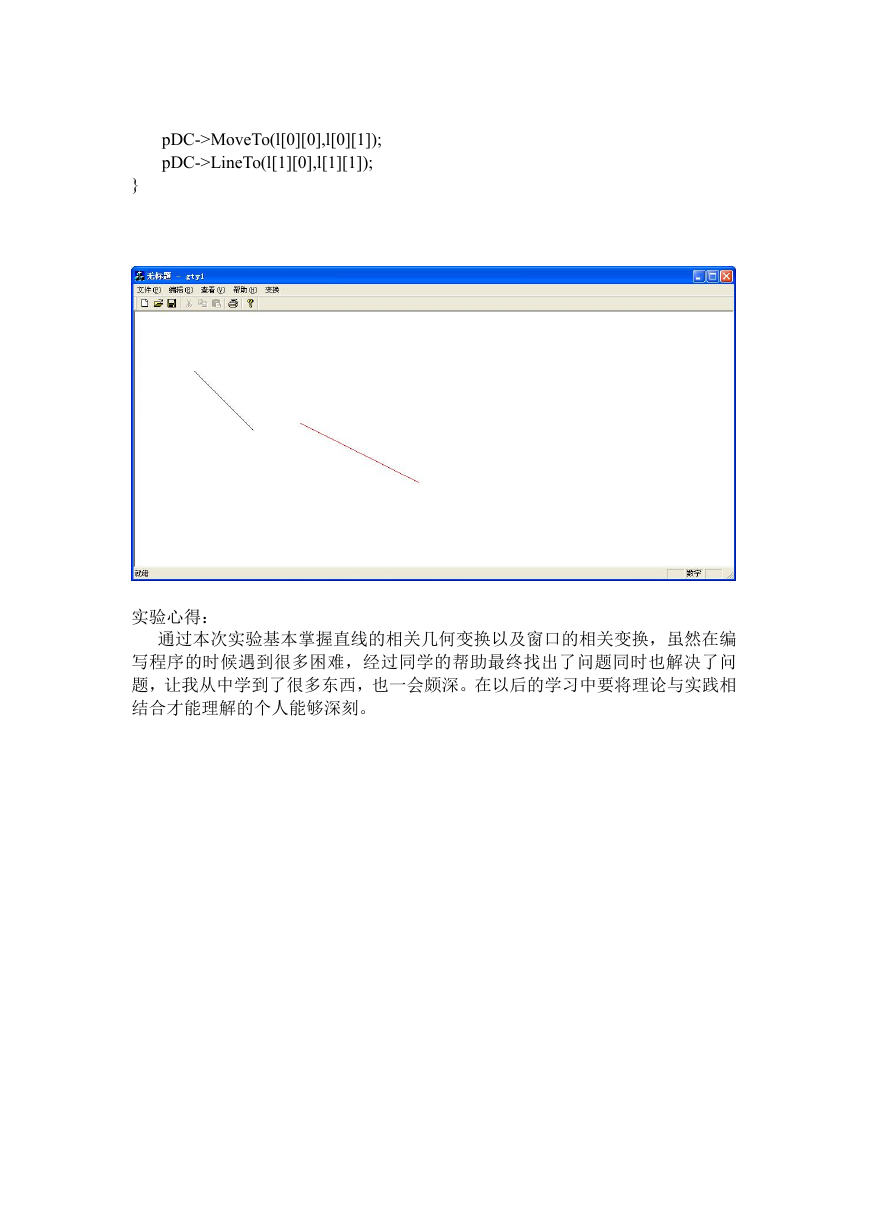
pDC->MoveTo(l[0][0],l[0][1]); pDC->LineTo(l[1][0],l[1][1]); } 实验心得：通过本次实验基本掌握直线的相关几何变换以及窗口的相关变换，虽然在编写程序的时候遇到很多困难，经过同学的帮助最终找出了问题同时也解决了问题，让我从中学到了很多东西，也一会颇深。在以后的学习中要将理论与实践相结合才能理解的个人能够深刻。

分享到：

赞收藏

资料库

计算机图形学图形变换.doc

相关推荐

课程资源

热门标签

最新资料