2 2 3 2 2 第 22卷 　第 4期 　　　　　　　　航天医学与医学工程 　　　　　　　 Vol. 22　No. 4 　2009年 　8月 　　　　　　Space M edicine & Medical Engineering　　 　　　Aug. 2009　 心电信号 QRS波精确定位算法研究 林海平 1 ,向 　馗 2 ,陈 　静 2 (1. 温州职业技术学院 ,浙江温州 325000; 2. 武汉理工大学自动化学院 ,湖北武汉 430070) 摘要 :目的 研究心电信号 QRS复波检测中单个波形起始和终止位置的精确判定 。方法 为了在动态心 电监护中设计信号自动分析算法 ,本文以滤波积分后所形成的窗口为基准 ,从滤波结果中获取 Q 波和 S 波波峰的准确位置 。结果 以此为基础 ,在波峰处引入一条简单的辅助直线 ,用直线和 ECG波形之间的 垂直距离作为判断 Q波和 S波边界的依据 。结论 大量数据检验结果表明 ,该计算法具有计算简便 ,误 差率低等优点 ,约为 1个采样点 。与国际通用软件相比 ,其 S波边界定位精度有显著提高 。 关键词 : QRS波 ;定位 ;动态心电图 中图分类号 : R857 3; TP391　　文献标识码 : A 　　文章编号 : 1002 0837 (2009) 04 0286 05 p ing, X IANG Kui, CHEN J ing. Space R esea rch on P rec ise L oca tion A lgo rithm fo r Q RS in ECG. L IN Hai Medicine & Medical Engineering, 2009, 22 (4) : 286～290 Abstract: O bjective To research the p recise location algorithm of onset and end of one wave for QRS in ECG. M ethods During monitoring the ambulatory electrocardiograph (AECG) , it was necessary to design new auto matic analysis algorithm s. The w indows formed by filtering and integrating p rocess could be considered as the the apex of Q wave and S wave could be recognized. Results Introducing fiducially mark. From the w indow, an auxiliary line from the apex, we could judge the boundary of the Q and S wave with the distance from ECG curve to the line. Conclusion Many cases studies inelicate that the algorithm is of low level locating error, a bout one samp le point, and the accuracy of judgement of S wave boundary is raised obviously compared with the same kind of software in the world. Key words: QRS comp lex; Address repr in t requests to: L IN Hai China p ing. W enzhou Vocational & Technical College, W enzhou 325005, location; ambulatory electrocardiograph 　　从 ECG中定义出与猝死相关的指标 ,一直是 生物医学领域的重要课题 。如何有效检测这些指 标 ,则主要是信号处理与建模的问题 ,其中最重要 当属 QRS检测 [ 1 ] 。常见的心性猝死指标包括 :心 率变异性 ( heart rate variability, HRV ) ;心率震荡 ( heart rate turbulence, HRT) ; 心室晚电位 ( ven tricular late potential, VLP) ; QT间期综合症 (QT syndrome, QTS ) ; T 波 交 替 ( T wave alternant, TWA ) 。从表 1 关于猝死指标的分析中可以看 出 , QRS复波的检测是所有分析算法的前提 ,而波 形定位的精度将直接影响指标的可信度 。 　　心电医学中关于猝死的检测指标较多 ,这些 指标获取都依赖于 QRS复波的检测 。QRS复波 的检测算法大致可以分为 3 类 : 差分和滤波方 法 [ 2 ] 、小波分析 [ 3 ]和智能计算 [ 4 5 ] ,其中前两种方 法应用较为普遍 。 Tompkins[ 6 ]关于 QRS功率谱 修回日期 : 2009 通讯作者 :林海平 　lhpxypa@126. com 15 05 基金项目 : 浙江省科技计划 ( 2008C21073 ) ; 温州市科技计划 ( G20070047) 的研究工作奠定了差分滤波及小波分析算法的基 础 : QRS波的能量主要集中在 5～11 Hz之间 。截 至目前 , Pan和 Tompkins[ 7 ]的基于带通滤波和非 线性变换的算法 (简称 PT算法 )仍然具有很大的 影响力 [ 8 9 ] 。在线分析动态心电图时 ,有明确的实 时性要求 ,再加上能耗限制 ,不允许使用过于复杂 的算法 。 经过 30 多年的反复研究 ,很多 QRS复波检 测算法的准确率已经达到 99%以上 。目前 ,主要 研究集中在单个波形的准确定位上 。波形定位主 要包括波形峰值 、起点和终点位置的确定 ,它是猝 死指标检测的基础性工作 。波形峰值的检测方法 表 1　猝死指标特性分析 Table 1　Fea ture ana lysis of SCD index SCD index waveform related detection contents HRV HRT VLP QTS TWA QRS, R QRS, R QRS, S and T QRS, Q and T QRS, S and T RR interval RR interval ST segment QT interval T waveform 

第 4期 　　　　　　　　　　　　　　　林海平 心电信号 QRS波精确定位算法研究 782 主要有 2 种 : 1 ) 用 设 定 的 阈 值 判 定 波 形 的 峰 值 [ 10 11 ] ; 2)通过某些特殊的变换来确定峰值位 置 [ 12 13 ] 。QRS事件检测往往以 R 波波峰为准 ,因 此 ,波形峰值定位算法研究较多 ,而关于波形边界 的研究较少 。R波作为 ECG单拍节律的最高点 , 常作为其余波形定位的基点 。在检测其余峰值 时 ,除了设置阈值以外 ,更重要的是限定一个合适 的区间 ,把区间内的极值作为波形峰值 ,以尽量避 免异常波形导致的误检 。关于波形边界的定位 , 以启发式或智能算法为主 ,缺乏有普遍说服力的 方法 。 本文主要研究 Q、R 和 S波的定位问题 , ECG 数据中 ,各个子波前后相连 ,并没有明显的分界 线 。波形的边界位于等电位线上 ,容易受到噪声 干扰 ,在动态心电中干扰尤为严重 。由于导联的 限制 ,动态监护中同步采集的通道较少 ,加上运算 能力的局限和实时性的要求 ,用做波形定位的往 往是单通道数据 。多方面因素使定位算法的设计 面临较大的困难 。 方 　法 PT算法 PT算法主要包括带通滤波和非线性变换 。 带通滤波可以由高通和低通滤波串联而成 ,非线 性变换包括差分 、平方和积分 。基本流程如图 1 所示 。用带通滤波来预处理 ECG,以凸显 QRS复 波成 分 , 其 理 论 基 础 源 于 Tompkins 等 [ 14 ] 关 于 ECG功率谱的研究 。在早期的有关文献中 ,带通 滤波都采用了整系数滤波器 ,主要是受运算能力 的限制 。滤波的目的主要是削弱 T波 、P波 、基线 漂移 、运动伪迹的影响 ,对于截止频率和衰减性能 并没有很高要求 。 　　文献 [ 14 ]中 PT算法以 200 Hz采样频率为 例 ,现在 ECG的采样频率远高于此 。在此我们以 1 000 Hz为例 (这也是我们在监护仪研发中使用 的采样频率 ) ,给出 PT算法的公式 。 PT算法在判 图 1　PT算法的基本步骤 F ig. 1　Ba sic steps of PT a lgor ithm 定 R 波时 ,有一套阈值设置和自动更新的方法 。 该方法已被反复验证 ,且与本文的 Q、S波定位关 联不大 ,在此略去不谈 。 ( 1 - z26 ) 2 ( 1) H ( z) = 676 (1 - z- 1 ) 2 H ( z) = z- 64 - ( 1 - z64 ) 2 4096 (1 - z- 1 ) 2 H ( z) = 0. 1 (2 + z- 1 - z- 3 - 2z- 4 ) y ( nT) = [ x ( nT) ]2 y ( nT) = 1 N N - 1 ∑ i = 0 x ( nT - iT) ( 2) ( 3) ( 4) ( 5) 平方操作使所有处理过的信号为正值 ,非线 性地放大了微分处理器的输出 。由于 T波往往也 具有较大的幅值 ,积分后 T波的幅度和 QRS的幅 度有可能比较接近 ,这给后续的阈值设置带来了 困难 。平方运算前的小小改进措施会有助于拉大 两者之间的差距 ,提高 R 波检测的准确性 。取一 个经验参数 k,使得 k·xT ( nT) < 1, k·xR ( nT) > 1 ( xT ( nT) 表示 T波幅度 , xR ( nT)表示 R波幅度 ) 。 另外 ,考虑到现在计算能力的富裕 ,在公式 ( 2)的 高通滤波器设计中适当提高了滤波器的阶数 。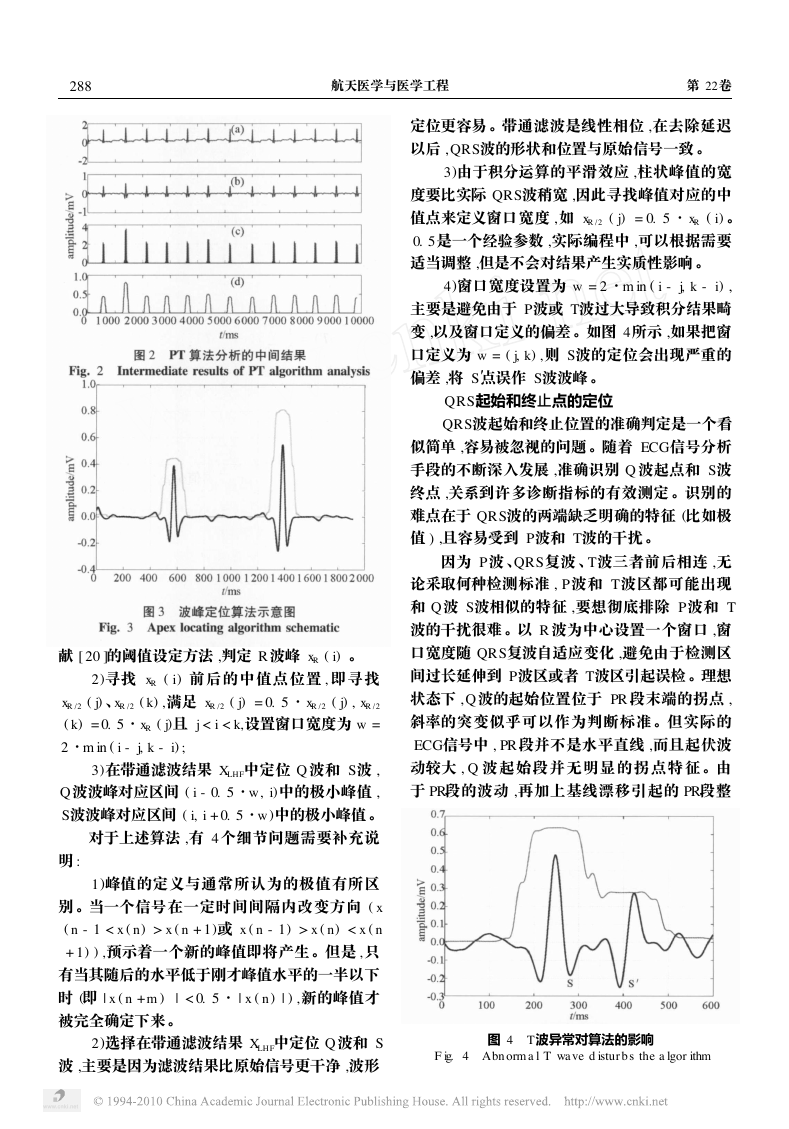 　　波峰定位算法 任意选择一组 ECG数据 , 按照公式 ( 1 ) ～ (5)依次处理原始数据 ,得到图 2 的结果 。观察 图 2b可以发现 ,带通滤波有效削弱了 T P段信号 的强度 ,而且 QRS的形状并没有发生变化 。图 2c 中差分和平方处理强化了 R 波两翼的大斜率特 性 ,并在 QRS波的位置形成了一组峰值 。图 2d 中 ,积分处理将相互分裂的峰值聚合起来 ,在 QRS 波对应的区域形成了一个类似柱状图的结果 ,非 常有利于 R波的判定 。 基于图 2d 的结果 ,我们分析并设计了 Q、S 波波峰的定位算法 ,如图 3所示 。 　　在确认了 QRS复波事件后 , R 波峰对应柱状 图形成的矩形窗口中的极大值 ,比较容易判定其 位置 。Q波和 S波容易受到运动伪迹和肌肉噪声 的干扰 ,经典滤波方法很难清除这些干扰 。因此 , 需要在 R波附近设置一个窗口 ,把定位 Q 波和 S 波的搜索范围严格限定在窗口内 。结合图 3,得 到下列算法 : 1 )在积分结果 X Int中寻找极大峰值 ,根据文 

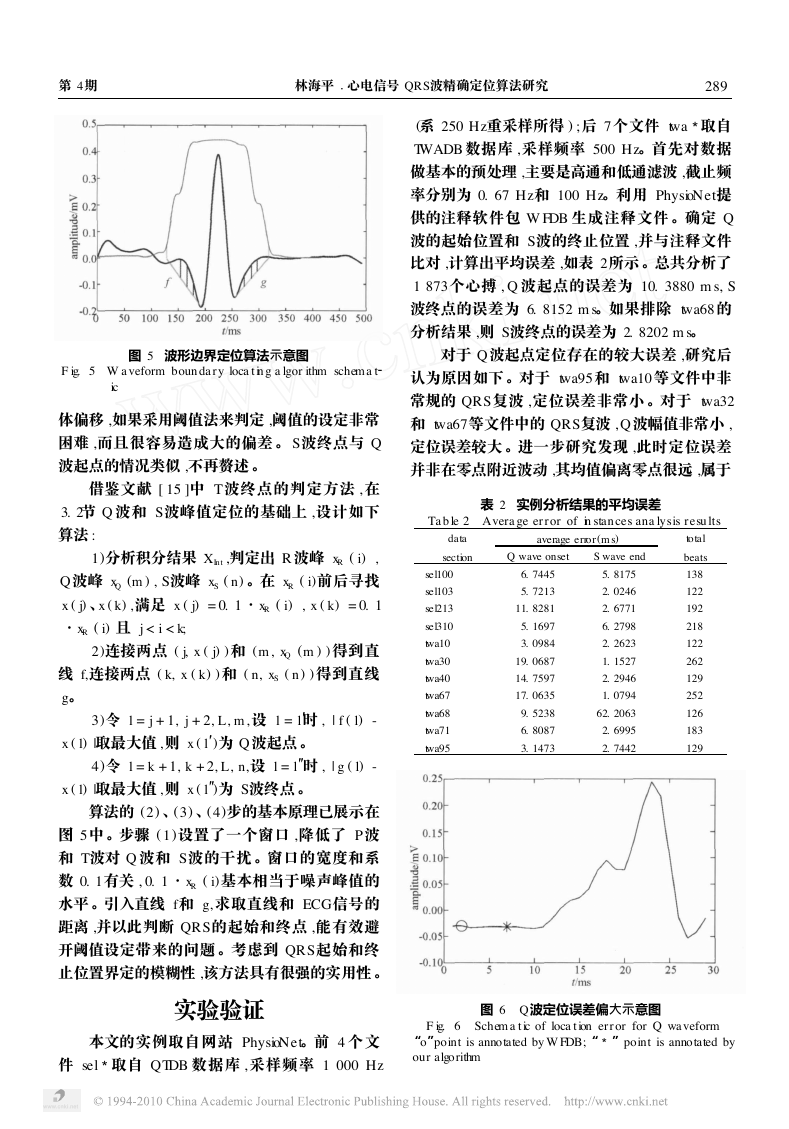
882 　　　　　　　　　航天医学与医学工程 　　　　　　　　　　　　　　　　　　第 22卷 定位更容易 。带通滤波是线性相位 ,在去除延迟 以后 , QRS波的形状和位置与原始信号一致 。 3)由于积分运算的平滑效应 ,柱状峰值的宽 度要比实际 QRS波稍宽 ,因此寻找峰值对应的中 值点来定义窗口宽度 ,如 xR /2 ( j) = 0. 5 ·xR ( i) 。 0. 5是一个经验参数 ,实际编程中 ,可以根据需要 适当调整 ,但是不会对结果产生实质性影响 。 4)窗口宽度设置为 w = 2 ·m in ( i - j, k - i) , 主要是避免由于 P波或 T波过大导致积分结果畸 变 ,以及窗口定义的偏差 。如图 4所示 ,如果把窗 口定义为 w = ( j, k) ,则 S波的定位会出现严重的 偏差 ,将 S′点误作 S波波峰 。 QRS起始和终止点的定位 QRS波起始和终止位置的准确判定是一个看 似简单 ,容易被忽视的问题 。随着 ECG信号分析 手段的不断深入发展 ,准确识别 Q 波起点和 S波 终点 ,关系到许多诊断指标的有效测定 。识别的 难点在于 QRS波的两端缺乏明确的特征 (比如极 值 ) ,且容易受到 P波和 T波的干扰 。 因为 P波 、QRS复波 、T波三者前后相连 ,无 论采取何种检测标准 , P波和 T波区都可能出现 和 Q波 S波相似的特征 ,要想彻底排除 P波和 T 波的干扰很难 。以 R 波为中心设置一个窗口 ,窗 口宽度随 QRS复波自适应变化 ,避免由于检测区 间过长延伸到 P波区或者 T波区引起误检 。理想 状态下 , Q波的起始位置位于 PR 段末端的拐点 , 斜率的突变似乎可以作为判断标准 。但实际的 ECG信号中 , PR段并不是水平直线 ,而且起伏波 动较大 , Q 波起始段并无明显的拐 点特 征 。由 于 PR段的波动 ,再加上基线漂移引起的 PR段整 图 4　T波异常对算法的影响 F ig. 4　Abnorma l T wave d isturbs the a lgor ithm 献 [ 20 ]的阈值设定方法 ,判定 R波峰 xR ( i) 。 2)寻找 xR ( i) 前后的中值点位置 , 即寻找 xR /2 ( j) 、xR /2 ( k) ,满足 xR /2 ( j) = 0. 5·xR /2 ( j) , xR /2 ( k) = 0. 5·xR ( j)且 j < i < k,设置窗口宽度为 w = 2·m in ( i - j, k - i) ; 3)在带通滤波结果 XLHF中定位 Q 波和 S波 , Q波波峰对应区间 ( i - 0. 5·w, i)中的极小峰值 , S波波峰对应区间 ( i, i + 0. 5·w )中的极小峰值 。 对于上述算法 ,有 4个细节问题需要补充说 明 : 1)峰值的定义与通常所认为的极值有所区 别 。当一个信号在一定时间间隔内改变方向 ( x ( n - 1 < x ( n) > x ( n + 1)或 x ( n - 1) > x ( n) < x ( n + 1) ) ,预示着一个新的峰值即将产生 。但是 , 只 有当其随后的水平低于刚才峰值水平的一半以下 时 (即 | x ( n +m ) | < 0. 5· | x ( n ) | ) , 新的峰值才 被完全确定下来 。 2)选择在带通滤波结果 XLHF中定位 Q波和 S 波 ,主要是因为滤波结果比原始信号更干净 ,波形 

3 第 4期 　　　　　　　　　　　　　　　林海平 心电信号 QRS波精确定位算法研究 3 图 5　波形边界定位算法示意图 F ig. 5　W aveform boundary loca ting a lgor ithm schema t ic 体偏移 ,如果采用阈值法来判定 ,阈值的设定非常 困难 ,而且很容易造成大的偏差 。 S波终点与 Q 波起点的情况类似 ,不再赘述 。 借鉴文献 [ 15 ]中 T波终点的判定方法 , 在 3. 2节 Q 波和 S波峰值定位的基础上 ,设计如下 算法 : 1)分析积分结果 X Int ,判定出 R 波峰 xR ( i) , Q波峰 xQ (m ) , S波峰 xS ( n) 。在 xR ( i)前后寻找 x ( j) 、x ( k) ,满足 x ( j) = 0. 1·xR ( i) , x ( k) = 0. 1 ·xR ( i) 且 j < i < k; 2)连接两点 ( j, x ( j) )和 (m , xQ (m ) )得到直 线 f,连接两点 ( k, x ( k) )和 ( n, xS ( n ) )得到直线 g。 3)令 l = j + 1, j + 2, L, m , 设 l = l′时 , | f ( l) - x ( l) |取最大值 ,则 x ( l′)为 Q波起点 。 4)令 l = k + 1, k + 2, L, n,设 l = l″时 , | g ( l) - x ( l) |取最大值 ,则 x ( l″)为 S波终点 。 算法的 (2) 、(3) 、(4)步的基本原理已展示在 图 5中 。步骤 ( 1)设置了一个窗口 ,降低了 P波 和 T波对 Q 波和 S波的干扰 。窗口的宽度和系 数 0. 1有关 , 0. 1 ·xR ( i)基本相当于噪声峰值的 水平 。引入直线 f和 g, 求取直线和 ECG信号的 距离 ,并以此判断 QRS的起始和终点 ,能有效避 开阈值设定带来的问题 。考虑到 QRS起始和终 止位置界定的模糊性 ,该方法具有很强的实用性 。 实验验证 本文的实例取自网站 PhysioNet。前 4 个文 取自 QTDB 数据库 ,采样频率 1 000 Hz 件 sel 982 (系 250 Hz重采样所得 ) ;后 7个文件 twa 取自 TWADB 数据库 ,采样频率 500 Hz。首先对数据 做基本的预处理 ,主要是高通和低通滤波 ,截止频 率分别为 0. 67 Hz和 100 Hz。利用 PhysioNet提 供的注释软件包 W FDB 生成注释文件 。确定 Q 波的起始位置和 S波的终止位置 ,并与注释文件 比对 ,计算出平均误差 ,如表 2所示 。总共分析了 1 873个心搏 , Q 波起点的误差为 10. 3880 m s, S 波终点的误差为 6. 8152 m s。如果排除 twa68 的 分析结果 ,则 S波终点的误差为 2. 8202 m s。 对于 Q波起点定位存在的较大误差 ,研究后 认为原因如下 。对于 twa95和 twa10等文件中非 常规的 QRS复波 ,定位误差非常小 。对于 twa32 和 twa67等文件中的 QRS复波 , Q波幅值非常小 , 定位误差较大 。进一步研究发现 ,此时定位误差 并非在零点附近波动 ,其均值偏离零点很远 ,属于 表 2　实例分析结果的平均误差 Table 2　Average error of in stances ana lysis results data section average error(m s) Q wave onset S wave end sel100 sel103 sel213 sel310 twa10 twa30 twa40 twa67 twa68 twa71 twa95 6. 7445 5. 7213 11. 8281 5. 1697 3. 0984 19. 0687 14. 7597 17. 0635 9. 5238 6. 8087 3. 1473 5. 8175 2. 0246 2. 6771 6. 2798 2. 2623 1. 1527 2. 2946 1. 0794 62. 2063 2. 6995 2. 7442 total beats 138 122 192 218 122 262 129 252 126 183 129 图 6　Q波定位误差偏大示意图 F ig. 6　Schema tic of loca tion error for Q waveform “o”point is annotated by W FDB;“ our algorithm ”point is annotated by 

092 　　　　　　　　　航天医学与医学工程 　　　　　　　　　　　　　　　　　　第 22卷 单向的偏差 。从 twa67 中选择一个心搏 ,如图 6 所示 ,“o”点和“ ”点分别源自 W FDB 软件和我 们的算法 。通过对标注结果的大量回放和分析表 明 ,W FDB 标注的 Q 波起点更偏向左边 ,处于明 显不合理的位置 。关于这一点 ,还需要在今后的 工作中做更深入的探讨 。 　　表 2中 , S波终点的定位效果普遍较好 ,唯有 twa68的定位结果偏差极大 。通过回放分析表明 , W FDB 将 T波顶点误作为 S波终点 ,属于比较明 显的错误结果 。 结 　论 通过上述大量的数据验证工作表明 ,本文提 出的 QRS波精确定位算法误差较小 ,相比广泛使 用的 W FDB软件 ,其 Q波起点定位结果更具合理 性 。可以为大量的猝死指标分析提供有力的支 持 。 [参考文献 ] [ 1 ] 　Kohler B, Hennig C, O rglmeister R. The p rincip les of software QRS detection[ J ]. IEEE Eng Med B iol, 21 (1) : 42 57. [ 2 ] 　A rzeno N, Deng Z, Poon C. Analysis of first IEEE T B io derivative based Med Eng, 2008, QRS detection algorithm s[ J ]. 55 (2) : 478 484. [ 3 ] 　Kadambe S, Murray R, Boudreaux based QRS comp lex detector[ J ]. form 1999, 46 (7) : 838 848. Bartels G. W avelet trans Med Eng, IEEE T B io [ 4 ] 　Sun Y, Chan K, Krishnan S. Characteristic wave detection in ECG signal using morphological transform [ J ]. BMC Cardio vasc D is, 2005, 5 (28) : 1 7. [ 5 ] 　M itra S, M itra M , Chaudhuri B. Pattern defined heuristic rules and directional histogram based online ECG parameter extrac tion[ J ]. Meas, 2009, 42 (1) : 150 156. [ 6 ] 　Thakor N,W ebster J, Tompkins W. Estimation of QRS com IEEE T B io p lex power spectra for design of a QRS filter[ J ]. Med Eng, 1984, 31 (11) : 702 [ 7 ] 　Pan J, Tompkins W. A real time QRS detection algorithm 706. [ J ]. IEEE T B io Med Eng, 1985, 32 (3) : 230 236. [ 8 ] 　Afonso X, Tompkins J, Nguyen Q, et al. ECG beat detection Med Eng, 1999, 46 (2) : IEEE T B io using filter banks[ J ]. 192 202. [ 9 ] 　Yeh Y,W ang W. QRS comp lexes detection for ECG signal: the difference operation method [ J ]. Comput Meth Prog B io. 2008, 91 (3) : 245 54. [ 10 ] 　Goutas A, Ferdi Y, Herbeuval J, et a l. D igital fractional or waves detection based algorithm for P and T der differentiation and delineation[ J ]. ITBM RBM, 2005, 26 (2) : 127 132. onset, T [ 11 ] 　Christov I, Simova I. Q end delineation: assessment of the performance of an automated method with the use of a reference database [ J ]. Physiol Meas. 2007, 28 ( 2 ) : 213 221. [ 12 ] 　Soria Maravilla J, et a l. App lication of adap tive signal p rocessing for determ ining the lim its of P and T waves in an ECG [ J ]. Med Eng, 1998, 45 (8) : 1077 O livas E, Martinez Sober M, Calpe IEEE T B io 1080. [ 13 ] 　XUE J. QT Interval measurement: what can we really expect In Computers in Cardiology, Valencia, Spain, 2006: 385 [ C ]. 388. [ 14 ] 　TompkinsW. B iomedical D igital Signal Processing[M ]. En glewood Cliffs, NJ: Prentice Hall, 1993. [ 15 ] 　Helfenbein E, Zhou S, L indauer J, et al. An algorithm for time QT interval monitoring[ J ]. J Electrocar continuous real diol, 2006, 39 (4) : 123 127. [作者简介 :林海平 ,女 ,副教授 ,研究方向为智能控制 ]