logo资料库

《数字电路与数字逻辑》复习（全知识点覆盖）.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：1.01M 资料格式：pdf 举报 版权申诉
第1页 / 共30页
第2页 / 共30页
第3页 / 共30页
第4页 / 共30页
第5页 / 共30页
第6页 / 共30页
第7页 / 共30页
第8页 / 共30页
资料共30页，剩余部分请下载后查看
    数字电子技术复习 一、数制与码制，以及它们之间的转换 1. 十进制转化为二进制： 整数部分除 2 取余，除基取余法：用目标数制的基数（R=2）去除十进制数。 先产生的余数为低位，后产生的余数为高位。 小数部分乘 2 取整：乘基取整法：小数乘以目标数制的基数（R=2），先产 生的整数靠近小数点，后产生的整数远离小数点。 2. 二进制与八进制、十六进制之间的转换 常用的编码：自然二进制码、二—十进制码、格雷码、奇偶检验码、ASCII 码等。 1）自然二进制码：按自然数顺序排列的二进制码。如用四位自然二进制码 0000—1111，表示十进制数 0—15。 2）二—十进制码（ Binary Coded Decimal Code，BCD 码）或称为 8421BCD 码，其的特点：位内是纯二进制编码，位间是十进制编码，故称这种编码方式为 二—十进制码。 3）ASCII 码（ American Standard Code for Information Interchange）：七位代 码表示 128 个字符，其中 96 个为图形字符，32 个控制字符。 4）格雷码（Gray Code)：二进制格雷码（也被称为二进制循环码）是一种 无权码，其特点是任何相邻的两个码字中仅有一位代码不同，其他代码是一样的， 所以二进制格雷码又叫单位距离码。二进制数中的第 i 位与第 i+1 位相同，则格 雷码的第 i 位为 0，否则为 1，二进制数的最高位必须与 0 相比较。 二、逻辑代数基础 1.逻辑代数中的基本运算（与或非）、复合逻辑运算（与非、或非、与或非）： 逻辑关系、逻辑真值表、逻辑表达式、逻辑符号 2. 逻辑代数的基本公式：公理、交换律、结合律、分配率、0-1 律、自等律、 互补律、重叠律、反演律、还原律、合并律、吸收律、包含律 3. 逻辑代数的 3 个重要运算规则 1）代入规则：将逻辑等式中的某一个逻辑变量全部用同一个逻辑函数代替， 则逻辑等式仍然成立。 2）反演规则：将逻辑函数 F 表达式中所有的“·”换成“+”，所有的“+ ”换成 “·”， 常量“1”换成“0”， “0”换成“1”，原变量换成反变量，反变量换成原变量，所得到 的逻辑函数就是 F 的非。 应用反演规则要注意：① 保持原函数的运算次序——先与后或，必要时适 当地加入括号；② 不属于单个变量上的非号的处理方法：非号保留，而非号下 面的函数式按反演规则变换。 3）对偶规则：将逻辑函数 F 表达式中所有的“·”换成“+”，所有的“+”换成 “·”， 常量“1”换成“0”，“0”换成“1”，而变量保持不变，所得到的逻辑函数就是 F 的对 偶式。 应用对偶定理时注意：求对偶式时运算顺序不变，且它只变换运算符和常量， 其变量是不变的。函数式中有“”和“⊙”运算符，求反函数及对偶函数时，要将 运算符“”换成“⊙”，“⊙”换成“”。 4. 逻辑函数及其表示方法 1）逻辑函数的定义：输入逻辑变量和输出逻辑变量之间的逻辑关系。F = f
    （A、B、C、……） 2）逻辑函数的特点：输入变量和输出变量只有逻辑 0、逻辑 1 两种取值。 3）逻辑函数的表示方法：真值表、逻辑函数式、逻辑图、波形图 5. 逻辑函数的标准形式 最小项的定义和表示 最小项：在 n 个变量的逻辑函数中，P 是 n 个变量的乘积项，如果在 P 中， 每个变量都以原变量或反变量的形式出现一次且仅出现一次，则称 P 为最小项， 3 个变量的逻辑函数有以下 8 个最小项。 6. 逻辑函数的化简：逻辑函数公式法化简、逻辑函数图形法化简 1）卡诺图化简法又称为图形化简法。该方法简单、直观、容易掌握，因而 在逻辑设计中得到广泛应用。 用卡诺图来表示逻辑函数，卡诺图的行坐标和列坐标没有按照纯二进制的顺 序，而是按照格雷码的顺序排列，从而卡诺图不但可以表示逻辑函数，而且可以 用卡诺图化简逻辑函数，并且直观、方便、准确。 n 个变量的函数的卡诺图有 2n 个小方格，分别对应 2n 个最小项； 几何上相邻的最小项在逻辑上也是相邻的。若两个最小项只有一个因子不 同，则称逻辑相邻。 相邻包括：直接相邻、上下相邻、左右相邻、四角相邻。 2）具有无关项的逻辑函数化简：约束项、任意项和逻辑函数式中的无关项 有些函数的输入变量不是任意的。对输入变量取值所加的限制称为约束。 任意项：函数可以随意取值（可以是 0、也可以是 1）或者不会出现的变量 取值组合所对应的最小项称为任意项。 无关项：通常约束项和任意项在逻辑函数中统称为无关项。 化简具有无关项的逻辑函数时，如果能合理利用这些无关项，一般都可得到 更加简单的化简结果。 三、逻辑门电路 1. MOS 管：MOS 管又称为绝缘栅型场效应三极管 （Metal-Oxide-Semiconductor Field Effect Transistor , MOSFET） MOS 管分为增强型和耗尽型两大类，每类又有 N 沟道和 P 沟道之分。它们 的工作原理基本相同。 NMOS 管和 PMOS 管的通断条件 NMOS 当 UGS＞VT 时导通；当 UGS＜VT 时截止 PMOS 当UGS＞VT 时导通；当UGS＜VT 时截止 VT 称为开启电压（T=Threshold,阈值） MOS 管的门极有非常高的输入阻抗。 2. CMOS（Complementary Metal Oxide Semiconductor），互补金属氧化物半 导体集成电路:是 NMOS 与 PMOS 组成的互补型电路。当前应用最广。 1）CMOS 非门的电路结构 2）CMOS 二输入或非门 每个 CMOS 门电路都是由 NMOS 电 路与 PMOS 电路两部分组合而成；并且 每个输入都同时加到一个 NMOS 管与一 个 PMOS 管的栅极上。 NMOS 管的串联可实现“与”操作，并
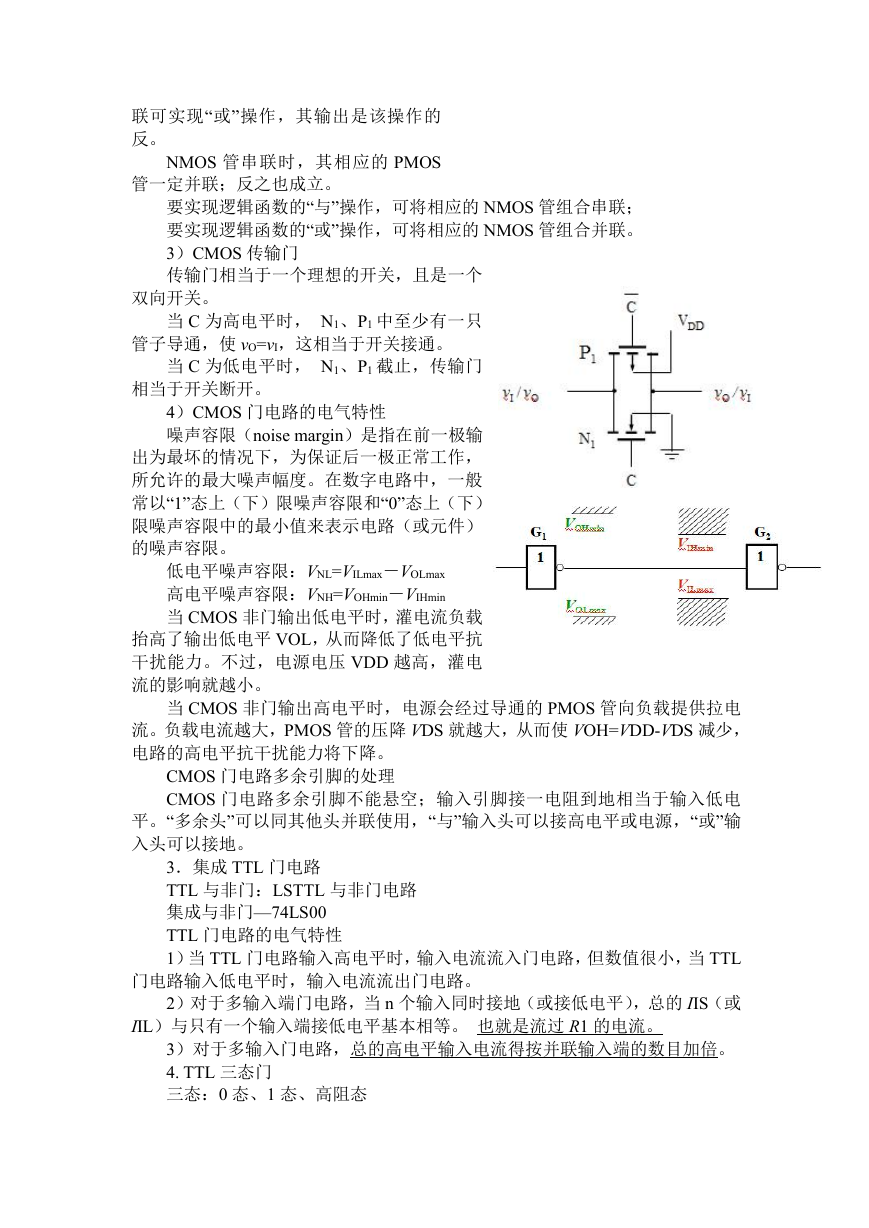
    联可实现“或”操作，其输出是该操作的 反。 NMOS 管串联时，其相应的 PMOS 管一定并联；反之也成立。 要实现逻辑函数的“与”操作，可将相应的 NMOS 管组合串联； 要实现逻辑函数的“或”操作，可将相应的 NMOS 管组合并联。 3）CMOS 传输门 传输门相当于一个理想的开关，且是一个 双向开关。 当 C 为高电平时， N1、P1 中至少有一只 管子导通，使 vO=vI，这相当于开关接通。 当 C 为低电平时， N1、P1 截止，传输门 相当于开关断开。 4）CMOS 门电路的电气特性 噪声容限（noise margin）是指在前一极输 出为最坏的情况下，为保证后一极正常工作， 所允许的最大噪声幅度。在数字电路中，一般 常以“1”态上（下）限噪声容限和“0”态上（下） 限噪声容限中的最小值来表示电路（或元件） 的噪声容限。 低电平噪声容限：VNL=VILmax－VOLmax 高电平噪声容限：VNH=VOHmin－VIHmin 当 CMOS 非门输出低电平时，灌电流负载 抬高了输出低电平 VOL，从而降低了低电平抗 干扰能力。不过，电源电压 VDD 越高，灌电 流的影响就越小。 当 CMOS 非门输出高电平时，电源会经过导通的 PMOS 管向负载提供拉电 流。负载电流越大，PMOS 管的压降 VDS 就越大，从而使 VOH=VDD-VDS 减少， 电路的高电平抗干扰能力将下降。 CMOS 门电路多余引脚的处理 CMOS 门电路多余引脚不能悬空；输入引脚接一电阻到地相当于输入低电 平。“多余头”可以同其他头并联使用，“与”输入头可以接高电平或电源，“或”输 入头可以接地。 3．集成 TTL 门电路 TTL 与非门：LSTTL 与非门电路 集成与非门—74LS00 TTL 门电路的电气特性 1）当 TTL 门电路输入高电平时，输入电流流入门电路，但数值很小，当 TTL 门电路输入低电平时，输入电流流出门电路。 2）对于多输入端门电路，当 n 个输入同时接地（或接低电平），总的 IIS（或 IIL）与只有一个输入端接低电平基本相等。 也就是流过 R1 的电流。 3）对于多输入门电路，总的高电平输入电流得按并联输入端的数目加倍。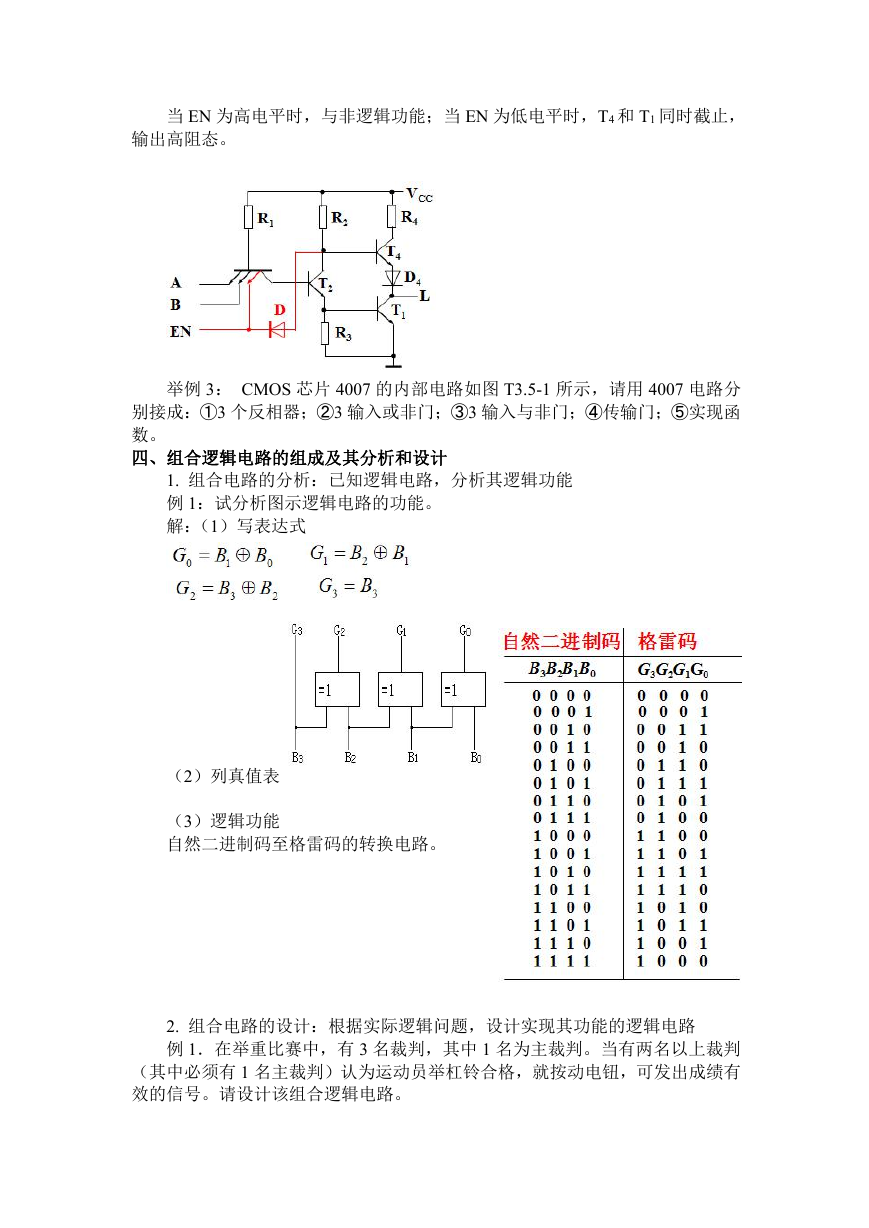 4. TTL 三态门 三态：0 态、1 态、高阻态
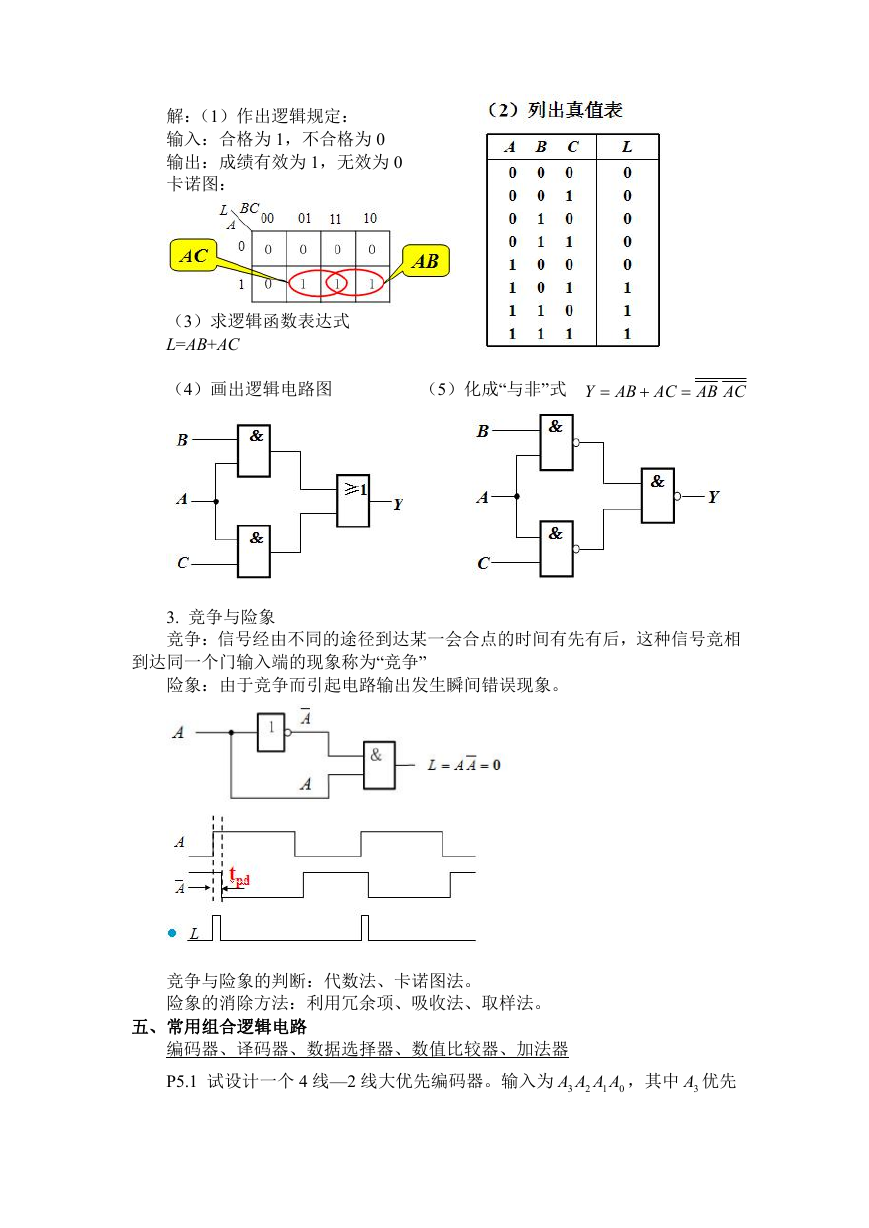
    当 EN 为高电平时，与非逻辑功能；当 EN 为低电平时，T4 和 T1 同时截止， 输出高阻态。 举例 3： CMOS 芯片 4007 的内部电路如图 T3.5-1 所示，请用 4007 电路分 别接成：①3 个反相器；②3 输入或非门；③3 输入与非门；④传输门；⑤实现函 数。 四、组合逻辑电路的组成及其分析和设计 1. 组合电路的分析：已知逻辑电路，分析其逻辑功能 例 1：试分析图示逻辑电路的功能。 解：（1）写表达式 （2）列真值表 （3）逻辑功能 自然二进制码至格雷码的转换电路。 2. 组合电路的设计：根据实际逻辑问题，设计实现其功能的逻辑电路 例 1．在举重比赛中，有 3 名裁判，其中 1 名为主裁判。当有两名以上裁判 （其中必须有 1 名主裁判）认为运动员举杠铃合格，就按动电钮，可发出成绩有 效的信号。请设计该组合逻辑电路。
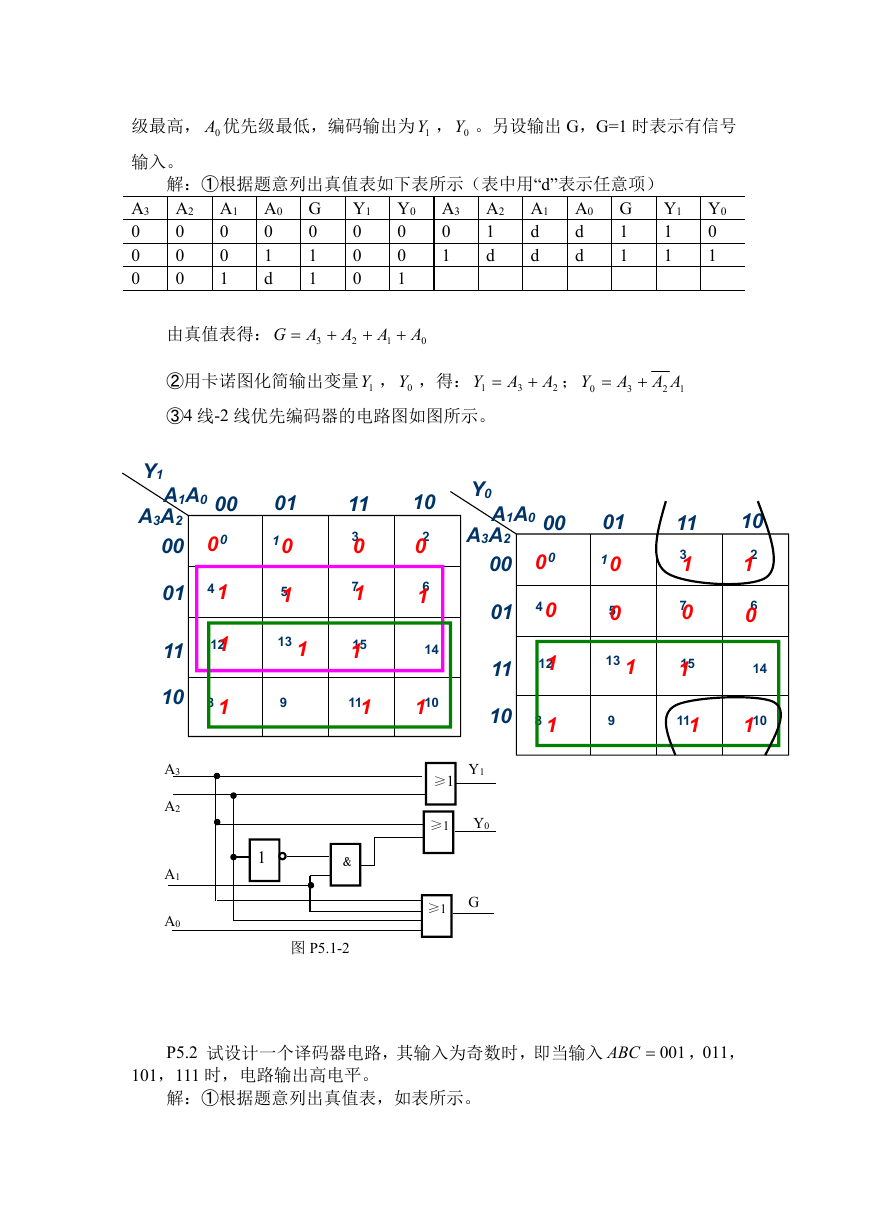
    解：（1）作出逻辑规定： 输入：合格为 1，不合格为 0 输出：成绩有效为 1，无效为 0 卡诺图： （3）求逻辑函数表达式 L=AB+AC （4）画出逻辑电路图 （5）化成“与非”式 Y  AB  AC  AB AC 3. 竞争与险象 竞争：信号经由不同的途径到达某一会合点的时间有先有后，这种信号竞相 到达同一个门输入端的现象称为“竞争” 险象：由于竞争而引起电路输出发生瞬间错误现象。 竞争与险象的判断：代数法、卡诺图法。 险象的消除方法：利用冗余项、吸收法、取样法。 五、常用组合逻辑电路 编码器、译码器、数据选择器、数值比较器、加法器 P5.1 试设计一个 4 线—2 线大优先编码器。输入为 AAAA 3 0 1 2 ，其中 3A 优先
    级最高， 0A 优先级最低，编码输出为 1Y ， 0Y 。另设输出 G，G=1 时表示有信号 输入。 解：①根据题意列出真值表如下表所示（表中用“d”表示任意项） A2 0 0 0 A0 0 1 d Y1 0 0 0 A1 0 0 1 Y0 0 0 1 A2 1 d A1 d d A3 0 1 G 0 1 1 A0 d d G 1 1 A3 0 0 0 Y1 1 1 Y0 0 1 由真值表得： AG 3   A 2  A 1  A 0 ②用卡诺图化简输出变量 1Y ， 0Y ，得： Y 1 ③4 线-2 线优先编码器的电路图如图所示。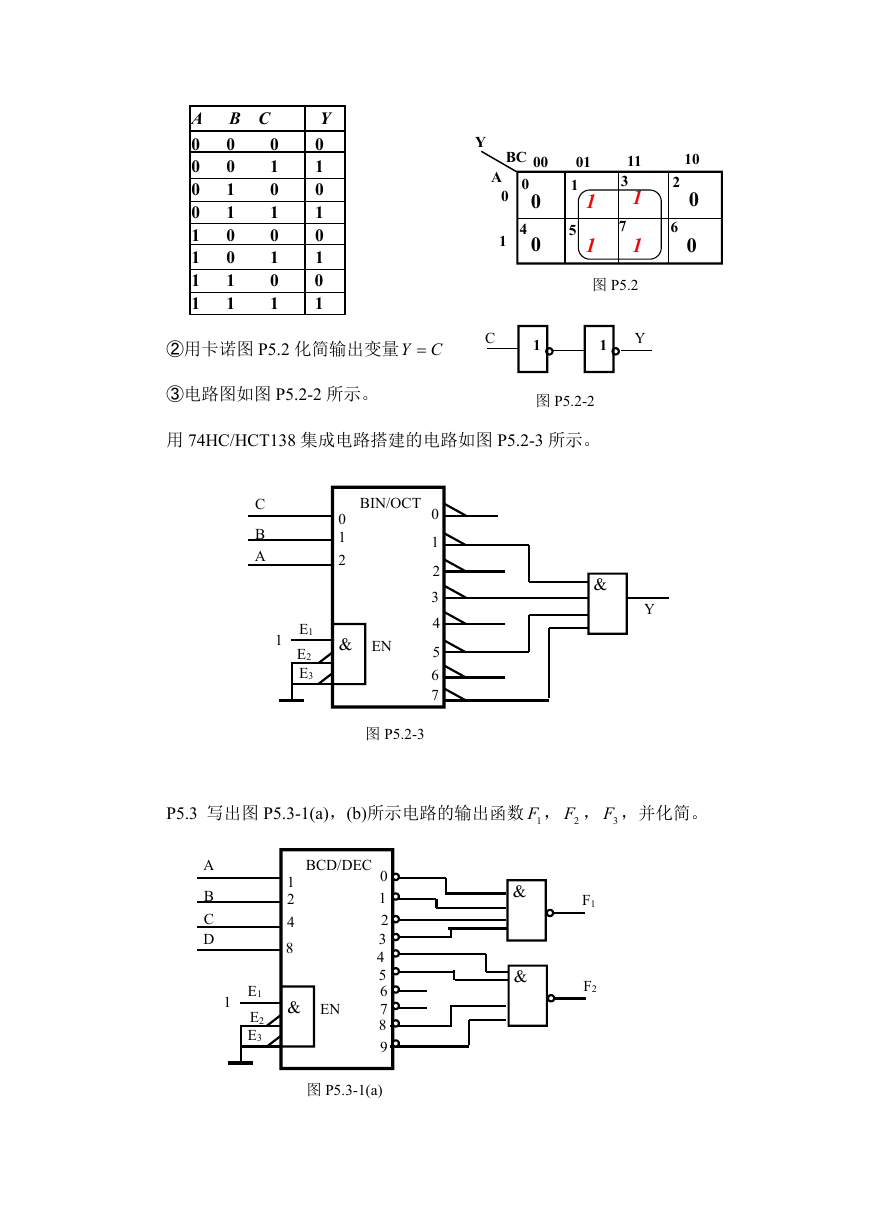  A 3  A 2 ； Y 0  A 3  AA 1 2 A1A0 Y1 A3A2 00 00 0 0 0 1 4 1 12 8 1 01 11 10 A3 A2 A1 A0 01 1 0 1 1 5 13 1 9 11 3 0 7 1 15 1 11 1 10 2 0 6 1 14 10 1 A1A0 Y0 A3A2 00 00 0 0 0 0 4 1 12 8 1 01 11 10 01 1 0 1 0 5 13 1 9 11 3 1 7 0 15 1 11 1 10 2 1 6 0 14 10 1 Y1 ≥1 ≥1 Y0 ≥1 G 1 ﹠ 图 P5.1-2 P5.2 试设计一个译码器电路，其输入为奇数时，即当输入 101，111 时，电路输出高电平。 ABC  001 ，011， 解：①根据题意列出真值表，如表所示。
    A 0 0 0 0 1 1 1 1 B C 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 Y 0 1 0 1 0 1 0 1 Y BC 0 A 0 4 1 00 0 0 01 1 1 5 1 11 3 1 7 1 2 6 10 0 0 图 P5.2 ②用卡诺图 P5.2 化简输出变量 CY  C 1 Y 1 ③电路图如图 P5.2-2 所示。 图 P5.2-2 用 74HC/HCT138 集成电路搭建的电路如图 P5.2-3 所示。 C B A BIN/OCT 0 1 2 1 E1 E2 E3  EN 图 P5.2-3 0 1 2 3 4 5 6 7  Y P5.3 写出图 P5.3-1(a)，(b)所示电路的输出函数 1F ， 2F ， 3F ，并化简。 A B C D BCD/DEC 1 2 4 8 1 E1 E2 E3  EN 0 1 2 3 4 5 6 7 8 9 图 P5.3-1(a)   F1 F2
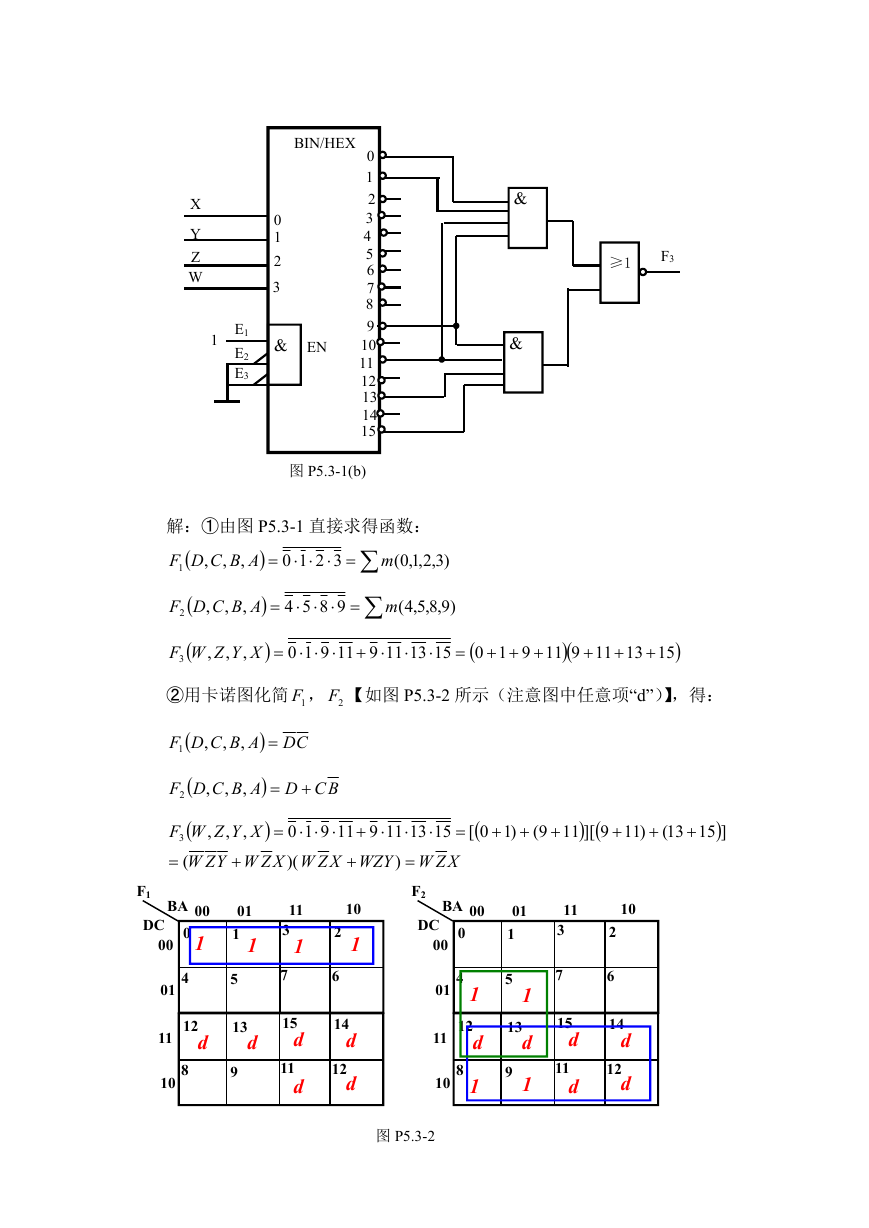
    BIN/HEX X Y Z W 0 1 2 3 1 E1 E2 E3  EN 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 图 P5.3-1(b)   ≥1 F3 解：①由图 P5.3-1 直接求得函数： ABCDF 1 3210  m )3,2,1,0(   , , ,   ABCDF 2 , , ,   9854  m )9,8,5,4(   XYZWF 3 11910 , , ,     119  13  15   910   9 11  11  13  15 ②用卡诺图化简 1F ， 2F 【如图 P5.3-2 所示（注意图中任意项“d”）】，得：    CDABCDF 1  , , , BCDABCDF 2   , , ,   , , ,  XYZWF  3 ( XZWXZWYZW  11910  )(     119  ) WZY F1 BA 0 DC 00 00 1 4 01 11 12 d 8 10 01 1 1 5 13 d 9 11 3 1 7 15 d 11 d 10 1 2 6 14 d 12 d  )10[  9(  11   9][  )11  13(   ]15 15 13    XZW  F2 BA 0 DC 00 00 01 11 4 1 12 d 8 10 1 图 P5.3-2 01 1 5 1 13 d 9 1 11 3 7 15 d 11 d 10 2 6 14 d 12 d
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料