论文研究-基于稀疏分解的近场源定位方法 .pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.35M 资料格式：pdf 举报版权申诉

weixin_39840914-11572925-4744302543423480491.pdf-第1页.png

第1页 / 共6页

weixin_39840914-11572925-4744302543423480491.pdf-第2页.png

第2页 / 共6页

weixin_39840914-11572925-4744302543423480491.pdf-第3页.png

第3页 / 共6页

weixin_39840914-11572925-4744302543423480491.pdf-第4页.png

第4页 / 共6页

weixin_39840914-11572925-4744302543423480491.pdf-第5页.png

第5页 / 共6页

weixin_39840914-11572925-4744302543423480491.pdf-第6页.png

第6页 / 共6页

文本预览

中国科技论文在线 http://www.paper.edu.cn 基于稀疏分解的近场源定位方法# 刘娟娟，王波，孙晓颖** （吉林大学通信工程学院，长春 130025）摘要：提出一种基于信源位置空间稀疏性的近场源定位方法。该方法通过利用贪婪算法对不同指向传感器阵列接收的数据进行重构，从而选择出与信源位置相关的原子，并根据原子的构造方法来确定信源的 DOA 和距离参数。提出方法对噪声具有鲁棒性，能有效处理相干源，且适用于快拍数较少的情况。通过仿真实验证实了该算法的有效性。关键词：近场源；DOA 估计；距离估计；稀疏表示；贪婪算法中图分类号：TN911.72 Near-Field Source Localization Method Based on Sparse Representation LIU Juanjuan, WANG Bo, SUN Xiaoying (College of Communication Engineering, Jilin University, Changchun 130025) Abstract: Based on the sparsity of the sources in the whole localization space, a new near-field source localization method is proposed. The method utilizes greedy algorithm for the signal received by each orientation dynamic array, then the atoms related to the localization of source are selected. With the construction method of atoms for selected atoms, we can estimate the DOA and range parameters of sources. Proposed method is robust to noise, and can effectively deal with the situations that the sources are coherent and the number of snapshots is smaller. The simulation results verify the effectiveness of proposed method. Key words: near-field source; DOA estimation; sparse representation; greedy algorithm 5 10 15 20 25 0 引言 30 35 信源定位是阵列信号处理的主要研究内容，在声纳、雷达、通信等领域有广泛的应用。当信源位于传感器阵列的近场区域[1]时，信号传播波前需用球面波来描述，此时信源的定位问题可以转化为估计信源的 DOA 和距离参数。针对近场源定位问题已经提出了很多有效的方法[2,3]。文献[2]提出的 2-D MUSIC 方法估计近场源参数，它需要 2-D 搜索，计算量较大；文献[3]则提出了高阶 ESPRIT 方法，该方法避免了多维搜索。以上子空间类方法有效的前提是需要大的快拍数并要求信源之间不相关。为了处理相干源，考虑将稀疏分解思想引入近场源定位中，其已经被有效用于远场源定位 [4,5,6,8]中处理相干源。[4]中提出 FOCUSS 方法，在单采样点情况下能有效估计信源 DOA。文献[5]提出适用于多采样点的 1 SVD 方法，此方法对噪声具有鲁棒性。[6]中提出基于压缩感知和动态传感器阵列的 DOA 估计方法，通过利用动态传感器阵列提高了分辨力。文献 [8]则利用贪婪类算法估计 DOA。 l − 本文将稀疏分解方法拓展到近场源定位中，提出一种利用动态传感器阵列的定位方法。该方法首先建立不同指向阵列对应的稀疏模型，再将贪婪算法[7]作用于各个稀疏模型并共同选择与信源位置相关的原子，得到信源的 DOA 和距离参数。该方法在低信噪比、较少快拍基金项目：教育部博士点新教师基金（200801831028）作者简介：刘娟娟（1988 — ），女，硕士研究生，主要研究方向：阵列信号处理通信联系人：王波（1975 — ），男，讲师，主要研究方向：阵列信号处理. E-mail: roywang@jlu.edu.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 40 数情况下仍有较高的估计精度，并且可以有效处理相干源。 1 信号模型 45 50 假设 L 个信号波长为λ的近场窄带信源入射到由 M 个阵元构成的动态均匀线阵上，阵元间隔为 d 。阵列以参考阵元为轴旋转，当与 x 轴之间的夹角为α时，称阵列指向为α。如图 1 所示，本文以阵元 1 为相位参考点，信源l 的 DOA 和距离参数表示为{ 阵元指向为α时接收信号的矩阵形式为 lrθ ，则 ,l } 1 1 , , α r a B 其中 ⎡ = ⎣ ) ( θ α 列流形矩阵，且 ) ( θ α exp … = a r j , , l l ( ⎡ 1 ⎢ ⎣ x = ( ) B s' t α α ) ( a , θ α r , l l ( ) t , + , a n α ( θ L ( ), t r , , , t ) , α L = （1） 1,2, N , 是指向为α的均匀线阵的阵 ⎤ ⎦ ( α ω l ( m ) 1 − + α φ l ( m − 2 ) 1 ) ) … exp ( ( α ω l ( j M ) 1 − + α φ l ( M 2 − ) 1 ) ) ⎤ ⎥ ⎦ T sin 2 π α ω = − l d 2 r λ l 是信号矢量， ( ) ⎡ t = ⎣ 指向为α的阵列第 m 个阵元的加性噪声， N 是快拍数。 ( θ α φ π d λ ( ) t ⎡ = ⎣ ( ) t ( ) t ( ) t α = l s' ⎤ ⎦ n − ) s s s α , , , T L 1 2 l 2 cos ) ( θ α − l n α 1 ( ) t , , α n M ( ) t ⎤ ⎦ ， ( ) mn tα 是信源l lr lθ 1 d α 2 m N-1 N x 图 1. 近场源动态阵列示意图 55 60 本文对信号模型作如下假设：（1）信源信号是相互独立的窄带平稳过程。（2） ( ) mn tα 为均值为零的高斯白噪声，各阵元之间的噪声相互独立，且独立于信号。（3）为了参数估计的唯一性，要求阵元间隔 2 提出算法 d λ≤ 4 将传感器阵列的近场范围分解成无数个可能的信源位置，而只有少数几个位置是有信号的，对整个近场范围可以看作是稀疏的，因此可以把定位问题作为一个稀疏求解问题。用 65 ),θ r 表示近场源信号所有 ( 可能的位置， θ r , ( ) = ⎡ ⎢ ⎢ ⎢ ⎢ ⎣ ( θ 1 r 1 ) , ( θ N r , - 2 - 1 θ ) ( θ 1 ) N r ( θ N θ r ) N r r , , ⎤ ⎥ ⎥ ⎥ ⎥ ⎦

中国科技论文在线 1θ ~ N θ θ 为将角度范围[ ) λ 的距离范围 0.62 D ( 1/2 3 ⎡ ⎣ http://www.paper.edu.cn − ，以 θ∆ 为间隔采样得到值， 1r ~ 89 90° ] ° ,2 D 2 ⎦ 以 r∆ 为间隔采样得到的采样值，且 ⎤ λ rNr 则是将阵列近场区域 ⋅ ，则可将 N Nθ << L r 70 75 80 （1）式写成稀疏形式 ( x α t α ) = Α 其中冗余字典 s α α t ( ) + n ( t ), α α t = （2） 1,2, α N α , ( θ 1 ) ,, α 1 1 , , , , , , α r r a a a θ r , r ( ) ,, α , θ a ) ( θ 1 ( ( a vec ⎡ Α = ⎢ ⎣ ⎡ = ⎢ ⎣ ) ( θ 2 ) ) ⎤ ,, α ⎥ ⎦ vec ⋅ 表示将矩阵按列矢量化。 ( ) s t α 是与信源位置相关的稀疏向量，t α表示阵列指向为α 时对信号的采样时间，不同指向的阵列采集的数据不同。在理想情况下，只有 L 个信源位置对应的值是非零的。通过求解稀疏问题（2）即可得到信源的位置。（3） ( ) ⎤ ⎥ ⎦ a r , , , N N T θ r r ( θ N ) ,, α 2 1 , , , } 考虑阵列是动态阵列，按一定的速度转换指向同时对信号进行采样，假设阵列有 I 个指向{ α α α ，基于（2）式可以构造 I 个稀疏表达式。对这 I 个稀疏表达式联合利 I 用贪婪算法 [7][9] 进行稀疏重构得到与信源位置相关的原子。利用文献[7] 中 S-OMP （Simultaneous Orthogonal Matching Pursuit）方法进行稀疏重构，算法步骤如下：（1）根据（3）式构造构造冗余字典{ （2）利用 S-OMP 算法联合对（2）式进行稀疏重构。具体步骤如下： a α α α I 。 } Α = , , , , a 1 2 a. 初始化。残差 r α = i x α i ( ), t i 数 0 k = 。 85 b. 挑选原子。计算 = ，挑选原子下标集index = ∅ ，挑选原子 1,2, I , 将 B i 元素按列相加得到矢量 B = Α i T r α α i i b ( p ) i N = ∑ q 1 = B i ( p q , ) 综合各个阵列的信息使 b 个原子使 b i ( max) ≥ b ( p ) p 1,2, = , N N ⋅ θ r ， I i b = ∑ 。挑选第 max i= 1 ， ( max) b i i 表示向量b 中的第 max i 元素 90 且使 i x = max index index ∪ c. 残差更新。 ( r = − Α ⋅ Α index 的原子，其中( Α k index α ( ) t d. α i i i † ) index α i ( ) t i ，其中 α x ( † ) ( = Α ) index α i * Α index α i index i αΑ 表示已经挑选出的 ) iαΑ 中下表为，( ) *⋅ 表示共轭转置。 index α Α ( ) 1 − * i i index α k= + ，如果 k L< (信源数)，返回到第（b）步。 1 95 （3）计算信源 DOA 及距离。根据式（3）中原子的下标与信源位置的对应关系求得信源 DOA 和距离。 - 3 -

中国科技论文在线 3 仿真实验 http://www.paper.edu.cn 15M = 的均匀线阵，阵元间距 α } ° 10 0 10 20 4α= 个间顺序循环转换，且按 θ∆ =1°，。假设阵列有 d λ= 4 ° ° ° 以下仿真试验中，考虑指向，按采样速度在指向 { = − r ∆ = 0.1 实验一：假设信源信号 ( ) t 构造冗余字典。 s λ 1 100 i e ϕ= 1 ( ) t 和 ( ) t s 2 i e ϕ= 2 ( ) t 互独立的，且在[ { rθ 20 ,16° , } { = 2 2 0,2π 之间服从均匀分布，信源位置分别为{ } λ ] 。本实验将提出方法与 2-D MUSIC 方法作对比。提出方法中每个指 } λ 1 向的阵列快拍数 aN = ，而 2-D MUSIC 方法只利用指向为 50 0 °α= 的阵列，且其快拍数取 1 tϕ 、 ( ) 的相位 ( ) 2 tϕ 之间是相 } { rθ , = − 和 20 ,8° 1 N 2 i s ∑ ( ) t σ 2 ⎛ ⎜ ⎝ t 1 = 256 。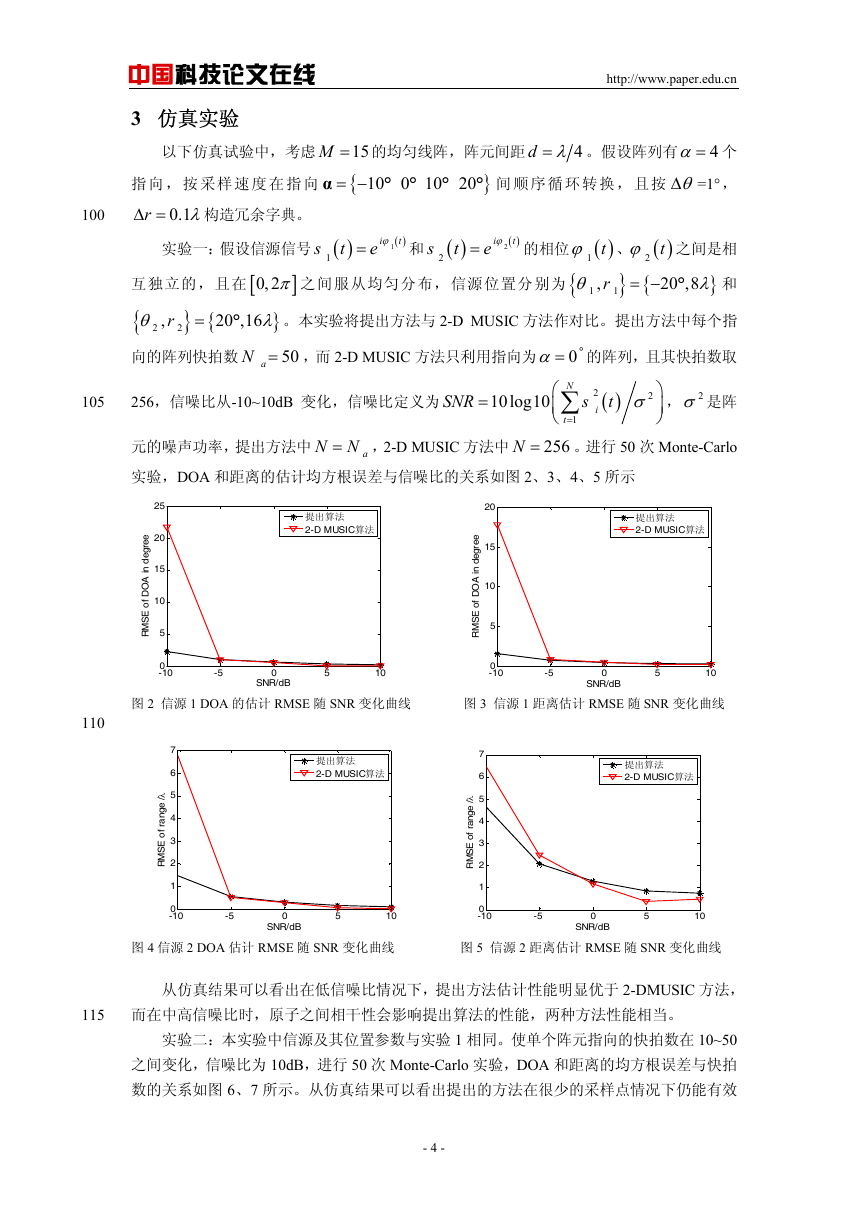进行 50 次 Monte-Carlo ， 2σ 是阵 ⎞ ⎟ ⎠ 105 256，信噪比从-10~10dB 变化，信噪比定义为 SNR = 10log10 元的噪声功率，提出方法中 N N= ，2-D MUSIC 方法中 a N = 实验，DOA 和距离的估计均方根误差与信噪比的关系如图 2、3、4、5 所示提出算法 2-D MUSIC算法 25 20 15 10 5 e e r g e d n i A O D f o E S M R 提出算法 2-D MUSIC算法 20 15 10 5 e e r g e d n i A O D f o E S M R 0 -10 -5 0 SNR/dB 5 10 0 -10 -5 0 SNR/dB 5 10 图 2 信源 1 DOA 的估计 RMSE 随 SNR 变化曲线图 3 信源 1 距离估计 RMSE 随 SNR 变化曲线 110 λ / e g n a r f o E S M R 7 6 5 4 3 2 1 0 -10 提出算法 2-D MUSIC算法 -5 0 SNR/dB 5 10 λ / e g n a r f o E S M R 7 6 5 4 3 2 1 0 -10 提出算法 2-D MUSIC算法 -5 0 SNR/dB 5 10 图 4 信源 2 DOA 估计 RMSE 随 SNR 变化曲线图 5 信源 2 距离估计 RMSE 随 SNR 变化曲线从仿真结果可以看出在低信噪比情况下，提出方法估计性能明显优于 2-DMUSIC 方法， 115 而在中高信噪比时，原子之间相干性会影响提出算法的性能，两种方法性能相当。实验二：本实验中信源及其位置参数与实验 1 相同。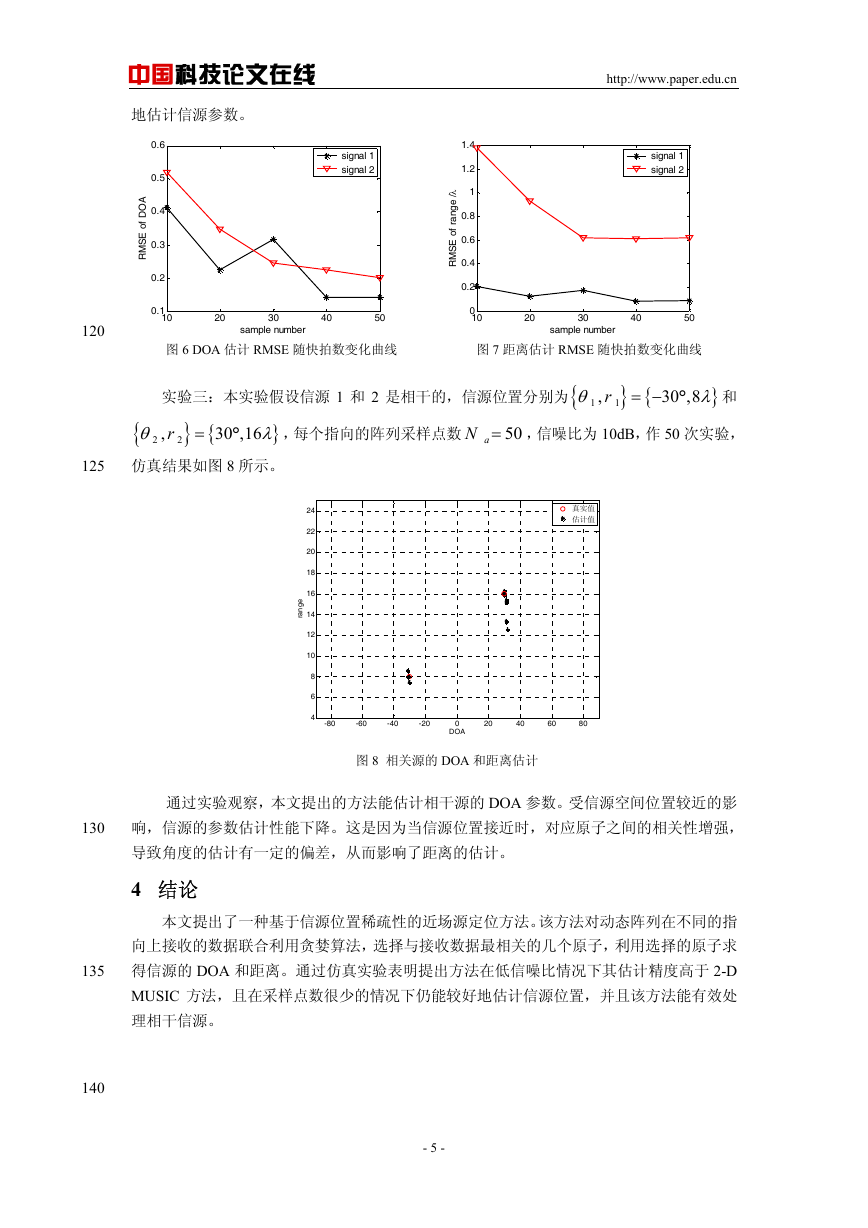使单个阵元指向的快拍数在 10~50 之间变化，信噪比为 10dB，进行 50 次 Monte-Carlo 实验，DOA 和距离的均方根误差与快拍数的关系如图 6、7 所示。从仿真结果可以看出提出的方法在很少的采样点情况下仍能有效 - 4 -

中国科技论文在线地估计信源参数。 0.6 0.5 A O D 0.4 signal 1 signal 2 f o E S M R 0.3 0.2 0.1 10 20 30 40 50 sample number http://www.paper.edu.cn signal 1 signal 2 20 30 40 50 sample number 1.4 1.2 1 0.8 0.6 0.4 0.2 0 10 λ / e g n a r f o E S M R 图 6 DOA 估计 RMSE 随快拍数变化曲线图 7 距离估计 RMSE 随快拍数变化曲线实验三：本实验假设信源 1 和 2 是相干的，信源位置分别为{ { } rθ , λ 仿真结果如图 8 所示。，每个指向的阵列采样点数 } { = 30 ,16° 2 2 aN = ，信噪比为 10dB，作 50 次实验， 50 rθ , 1 } { = − 1 30 ,8° } λ 和 e g n a r 24 22 20 18 16 14 12 10 8 6 4 真实值估计值 -80 -60 -40 -20 0 DOA 20 40 60 80 图 8 相关源的 DOA 和距离估计通过实验观察，本文提出的方法能估计相干源的 DOA 参数。受信源空间位置较近的影响，信源的参数估计性能下降。这是因为当信源位置接近时，对应原子之间的相关性增强，导致角度的估计有一定的偏差，从而影响了距离的估计。 4 结论本文提出了一种基于信源位置稀疏性的近场源定位方法。该方法对动态阵列在不同的指向上接收的数据联合利用贪婪算法，选择与接收数据最相关的几个原子，利用选择的原子求得信源的 DOA 和距离。通过仿真实验表明提出方法在低信噪比情况下其估计精度高于 2-D MUSIC 方法，且在采样点数很少的情况下仍能较好地估计信源位置，并且该方法能有效处理相干信源。 - 5 - 120 125 130 135 140

中国科技论文在线 http://www.paper.edu.cn [参考文献] (References) 145 150 155 [1] W. Zhi, M. Y. Chia. Near-field source localization via symmetric subarrays. IEEE Signal Processing Letters, 2007, 14(6): 409-412. [2] Y. D. Huang, M. Barkat. Near-field multiple source localization by passive sensor array. IEEE Transaction Antennas Propagation, 1991, 39(7): 968 - 975. [3] R. N. Challa, S. Shamsunder. High-order subspace-based algorithms for passive localization of near-field sources. in Proc. of 29th Asilomar Conf. Signals. Syst. Comput.. Pacific Grove, 1995, 2: 777-781. [4] I. Gorodnitsky, B. Rao. Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm. IEEE Transactions on Signal Processing, 1997, 45(3): 600 – 616. [5] D. Malioutov, M. Cetin, A.Willsky. A Sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Transaction on Signal Processing, 2005, 53(8): 3010 - 3022. [6] Bilik I. Spatial Compressive Sensing for Direction-of-Arrival Estimation of Multiple Sources using Dynamic Sensor Arrays. IEEE Transaction on Aerospace and Electronic Systems, 2011, 47(3): 1754 - 1769. [7] J. A. Tropp, A. C. Gilbert, M. J. Strauss. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit. Signal Processing, 2006, 86(3): 572 - 588. [8] G. Karabulut, T. Kurt, A. Yongacoglu. Angle of arrival detection by matching pursuit algorithm. IEEE Vehicular Technology Conference, 2004, 1:324 - 328. [9] S. F. Cotter, B. D. Rao, K. Engan, K. Kreutz-Delgado. Sparse Solutions to Linear Inverse Problems With Multiple Measurement Vectors. IEEE Transaction on Signal Processing, 2005, 53(7): 2477 – 2488. - 6 -

分享到：

赞收藏

资料库

论文研究-基于稀疏分解的近场源定位方法 .pdf

相关推荐

开发技术

热门标签

最新资料