第1页 / 共19页
第2页 / 共19页
第3页 / 共19页
第4页 / 共19页
第5页 / 共19页
第6页 / 共19页
第7页 / 共19页
第8页 / 共19页
权证的蒙特卡洛模型及实证分析.pdf
= 权证价格变动/标的股价格变动
=权证价格变动/标的资产对数收益的均值变动
Vega=权证价格变化/波动率的变化
Theta=权证价格变化/到期时间变化。
E=0;
D=0;
In this paper, We use the exponentially weighted moving average(EWMA) model to compute the parameters of Monte Carlo model. This Improve the precision of Monte Carlo model and prove that the recent data have more influence to the model than the early ...
Keywords: warrant, Monte Carlo model, EWMA, sensitivity analysis
中国科技论文在线
http://www.paper.edu.cn
权证的蒙特卡洛模型及实证分析
孙倩怡
中国矿业大学理学院，江苏徐州 (221116)
E-mail：sunqianyi916@163.com
摘 要：本文利用指数加权移动平均模型计算参数µ改进了蒙特卡洛模型，通过所选的五
粮 YGC1(030002)进行定价并比较定价结果，发现改进后模型的预测结果要明显优于原模型，
这也证实了近期历史价格数据对参数的影响要大于远期历史数据。最后本文对所选的五粮
YGC1(030002)进行敏感性分析，发现对于该认购权证，参数µ的影响要显著大于参数σ 。
关键词：权证；蒙特卡洛模型；指数加权移动平均模型；敏感性分析
中图分类号：O221
1．引言
2005 年 8 月 22 日，宝钢权证(580000)正式发行上市，阔别市场 11 年之久的权证市场重
新开闸。此后，宝钢、鞍钢、武钢、万科、新钢矾、白云机场等权证在深、沪交易所上市。
这也意味着经过十余年的探索与努力，我国金融衍生品市场发展进入了更高层次的阶段。在
我国过去近两年的牛市中，权证更以其高额的收益吸引了无数投资者的追捧，由武钢权证单
个交易日内涨幅达到 500%即可见一斑。但高收益必然伴随着高风险，因此对权证进行合理
的定价就显得尤为重要。
权证本质意义上就是一个期权，因此它的定价可以借用期权定价的方法来完成。针对期
权定价方法的研究有很多，其中包括 Black-Scholes 模型、二叉树定价模型、蒙特卡罗（Monte
Carlo）数值模拟模型、有限差分模型、有限元模型等等。蒙特卡罗数值模拟模型是众多模
型中较为简单实用的一种，也是金融界运用较为广泛的一种模型。本文将重点考察蒙特卡罗
数值模拟模型。蒙特卡罗数值模拟模型源于美国在第一次世界大战研制原子弹的"曼哈顿计
划"，是一种以概率统计理论为指导的一类非常重要的数值计算方法。随着各种“方差缩减”
技巧和“拟蒙特卡罗方法”的出现，其理论基础得到了完善。该方法因其结构简单、易于实现
等特点被广泛应用于各个领域，特别是在金融工程中用于对部分衍生产品的定价[1]。
本文的研究目的是对 Monte Carlo 数值模拟模型进行合理改进，使该模型既可以获得更
好的结果又更符合实际。利用 Monte Carlo 数值模拟模型对期权进行定价是基于标的资产价
格呈对数正态分布的假设，在考虑了行权价格、行权日及标的股价格对期权价格的影响后，
建立数学模型编程进行计算机模拟从而得出期权价格。但考虑到实际情况，近期历史数据对
模型的影响要大于远期数据，因此本文在初始 Monte Carlo 数值模拟模型的基础上利用指数
加权移动平均模型估计参数 µ。
本 文 的 数 据 选 取 五 粮 YGC1(030002) 为 权 证 定 价 的 研 究 对 象 ， 其 标 的 股 为 五 粮 液
(000858)，时间跨度为 2006 年 6 月 7 日至 2008 年 2 月 5 日，取中间每个交易日的收盘价作
为历史数据，并计算出对数收益率，用来估计参数。
2．权证定价理论简介
权证[2] [3] [4]
是一种权利凭证，投资者付出权利金购买权证后，有权利在某一特定时期或
时点按约定价格向发行人购买或卖出标的证券。权证持有人在支付权利金后获得的是一种权
利，而非义务，行使与否由其持有人自主决定；而权证发行人在权证持有人按规定提出履约
要求时，负有提供履约的义务，不得拒绝。根据不同标准，可以对权证进行不同分类。
按行使时间划分，权证有欧式和美式两种。欧式权证规定持有人只有在约定时间到达时
有权买卖标的资产，而美式权证则允许持有人在约定时间到达前的任意时间行使买卖标的资
-1-
中国科技论文在线
产的权利。目前我国上市交易的权证都为欧式权证。
http://www.paper.edu.cn
按权利行使方式划分，权证分为认购权证和认沽权证。对于认购权证，权证的持有人可
于约定的期间或到期日，以约定的价格认购该项权证的标的资产；而对于认沽权证，权证持
有人可于约定的期间或到期日，以约定的价格沽出该项权证标的资产。
按发行人的不同，权证分为股本权证和备兑权证。股本权证通常由上市公司自行发行，
备兑权证是由基础资产发行人以外的第三方发行的权证。现阶段，我国上市交易的权证绝大
部分都为备兑权证。
权证作为一种衍生金融证券产品，其本质就是一个期权。从而 我们可以用期权的定价理
论来讨论权证的定价，也就是权证的理论价值。一是定价方式相同，都受到标的资产价格、
履约价格、标的价格波动率、到期日和无风险利率等因素的影响；二是都具有风险管理功能，
如投资者防止股票价格下跌造成损失，可以买进认沽权证，也可以卖出认购权证，进行对冲，
无需进行股票现货买卖。三是都有杠杆效应，都具有以小搏大的功能，属于高风险、高收益
的产品。
3．Monte Carlo 数值模拟模型
3.1 蒙特卡罗模拟的基本原理
蒙特卡洛模拟方法的基本思想[6]
是, 将符合一定概率分布的大量随机数作为参数带入
数学模型, 求出所关注变量的概率分布, 从而了解不同变量对目标变量的综合影响以及目标
变量最终结果的统计特性。蒙特卡洛模拟方法的基本原理可简单描述如下:
假定函数
y
=
f x x
(
,
1
1
,...,
x
),n
蒙特卡洛模拟方法利用一个随机数发生器先生成一组样
x
本 值 11
(
,
x
21
,...,
x
n
1
),
然 后 按
y
=
f x x
(
,
1
1
,...,
x
),n
的 关 系 式 确 定 函 数 的 值
y
1
=
f x
(
11
,
x
21
,...,
x
)n
1
。反复独立抽样 (模拟) 多次 (
i =
1,2,....
)
, 便可得到函数的一组抽样
数据 1
y y
,
1
(
,...,
y 。当模拟次数足够多时, 便可给出与实际情况相近的函数 y 的概率分布
)n
与其数字特征。
应用蒙特卡洛模拟方法的前提是, 要确定目标变量的数学模型以及模型中各个变量的
概率分布。 如果确定了这两点, 就可以按照给定的概率分布生成大量的随机数, 并将它们代
入模型, 得到大量目标变量的可能结果, 从而研究目标变量的统计学特征。 因此, 应用蒙特
卡洛模拟方法的具体步骤为:
第一步 建立描述项目收益与若干影响因素之间的数学公式,称作蒙特卡洛分析模型。
第二步 确定蒙特卡洛分析模型的主要风险变量。
第三步 根据经验和历史数据, 求出各风险变量的概率分布。常用的概率分布有: 正态分布、
对数正态分布型、均一型和三角形,还有指数衰减型、用户自定义型。
第四步 用计算机按照给定的概率分布生成大量的随机数, 用这些随机数作为各变量的参数
代入分析模型, 求出预期收益(即模型的目标变量) 的值, 经过大量的模拟计算, 就可以得到
目标变量的概率分布及统计特征, 从而预测在众多因素影响下的预期收益率及其概率分布。
3.2 期权定价的蒙特卡洛模拟方法
在金融衍生证券的定价中，我们可根据非套利资产定价理论,将金融衍生证券的价格表
示为其有效期内贴现盈利收益的期望值.其中期望值是针对风险中性的概率测度而言的.如考
-2-
中国科技论文在线
http://www.paper.edu.cn
虑 欧 式 衍 生 证 券, 假 设 在 到 期 日 T 的 盈 利 收 益 为 Tf
,则 在 当 前 时 刻, 其 价 格 可 表 示 为
f
=
^
E
−
rT
−
Tf e
.其中
^
E 代表风险中性世界的期望值, r 为无风险利率.如果在到期日以内 r
为常数,则该式可写为
f
−=
e
−
rT
^
(
E f
T
)
.如果考虑美式衍生证券.假设 (
h sτ 表示τ时刻,标的
)
变量的值为 sτ时的盈利收益,则其价格可表示为
f
=
^
E
(
h s
)
τ
e
−
rT
−
.式中τ为该衍生证券
在其有效期内的可能执行时刻.同样,如假设 r 在该衍生证券的有效期内为常数时,则上式又
可写为
f
=
e
−
rT
−
^
E
(
h s
)
τ
.以上的公式在许多情况下也可表示为积分形式,蒙特卡罗模拟
就是通过模拟上述的期望值或积分值来估计衍生证券价格的。
3.3 蒙特卡罗方法在权证定价中的应用
蒙特卡洛方法在权证定价中的应用是基于资产价格呈对数正态分布的假设，重复模拟出
资产在权证持有期内的走势，得到资产在权证到期日的不同价格分布，由此根据权证在到期
日资产不同价格下的价值分布，再取权证在到期日的价值均值的现值作为权证的价格。
根据资产价格呈对数正态分布的假定，若我们已知资产在时间 t (0
则经过间隔 t∆ 后，资产的价格 t
tS +∆ 可由下式估计：
< < 的价格 tS ，
t T
)
t
∆ (3-1)
其中µ和σ分别为资产收益对数的均值和波动率，z 为服从标准正态分布的随机变量。
，从资产在权证签约日的价格 0S 开始，
将权证的持有期 T 分为 n 个间隔相等的时段
t T n
∆ =
+∆ =
z
µ σ
t
∆ +
exp(
S
)
S
t
t
t
/
重复利用公式（3-1）n 次可得资产在权证到期日的一个价格 TS ，记行权价格为 XS ，再利用
下面的公式：
认购权证
C =max(S
T
T
S−
X
,0)
(3-2 )
认沽权证
P
T
=max(S
X
S−
T
,0)
(3-3)
可得权证在到期日的一个价值，重复做这样的模拟 m 次，可得权证的 m 个可能的价值，记
无风险利率为 r，再取
即可得到权证的价格。
C E C e−
T[
=
]
rT
或
P E P e−
T[
=
]
rT
(3-4)
总结上述过程，我们可以得出蒙特卡罗数值模拟方法计算权证价格的过程如下：
（1）输入资产及权证的有关参数 0S ， TS ，T ，µ，σ，r ，时段数 n 和模拟次数 m，
并计算
t T n
∆ =
/
；
-3-
中国科技论文在线
http://www.paper.edu.cn
（2）关于 i =1，2，…，m 作下列模拟和计算，由式 1
k
+ =
S
S
k
exp(
z
µ σ
t
∆ +
∆ ，k =0，
t
)
1，…，n-1 从 0S 开始模拟得 T
S
C
S= ， T
n
=max(S
T
S−
X
,0)
P
或 T
=max(S
X
S−
T
,0)
；
（3）计算
E C 或 T[
T[
E P 。
]
]
在这一模拟过程中，存在着模拟次数和计算精度之间的矛盾。根据理论分析的要求，
在模拟时 t∆ 的长度应充分小，模拟的次数应尽可能多，以便使所得的资产价格估值尽可能
的涵盖资产价格的真实分布，但这样无疑会大大增加模拟的计算工作量。一般来说，对于存
续期限短的权证，我们可以取一个工作日作为时段的长度；对于期限相对较长的权证，可以
取一周或十个工作日作为时段，以减少模拟单个资产到期日价格所需的工作量，同时又能较
好的模拟资产的价格走势。对于模拟次数，一般要求不少于 1000 次，比较理想的次数在 5000
到 10000 之间。
3.4 方差缩减方法
在利用蒙特卡洛方法模拟标的资产的价格运动过程时需要生成大量的服从标准正态
分布的随机变量，并进行大规模运算。由于利用计算机进行仿真必然存在着计算误差以及舍
入误差，随着计算量的加大以及问题复杂程度的提高，蒙特卡洛方法的定价精度就会受到很
大的影响。为了提高算法处理误差的能力，获得高精度、稳定的结果，我们需要减小所产生
的随机数据的方差，这就导致了方差缩减方法[6]
的出现。
相反变量法是处理金融定价问题中一个最常用的、最简单的方差缩减技术。我们先通过
一个简单的例子来介绍该方法。
下面考虑利用计算机建立B.S.模型，对一个标的为无分红股票的欧式看涨期权进行定价
的问题。该模型虽然不需要通过计算机进行仿真模拟，我们仅以此作为介绍相反变量法思想
的例子。在B.S.模型中，股票价格服从对数正态分布。在风险中性度量下最终的股票价格可
以由以下公式得出。
i
TS
=
S e
0
(
r
−
(1/ 2)
σ σ
+
)
T
2
T Z
i
(3-5)
此处 0S 是当前股票的价格，r是无风险利率，σ 是股票价格的波动率，T是期权的有效
期，{ }iZ 是服从标准正态分布的独立样本。记行权价格为K，则在n次重复试验后得到一个
期权价格的无偏估计为：
ˆ
C
=
1
n
n
∑
i
1
=
−
rT
e
max{0,
i
S
T
−
K
}
(3-6)
因为{ }iZ 是服从标准正态分布的独立样本，由正态分布的性质可知{
}iZ− 也是服从正
态分布的独立样本。因此可以将 iZ− 代入公式（3-5）进行计算，得出对应于 iZ− 的 ˆi
价格同样可以作为一个有效的样本，进而由公式（3-6）得到 ˆ
max{0,
K
rT
−=
C e
i
TS ，该
i
S
T
− ，该
}
值 也 是 期 权 价 格 的 无 偏 估 计 。至 此 就 得 到 了2n 个 期 权 价 格 的 无 偏 估 计 值， 整 理 为
， 1,2
= 。
n
i
ˆ
C
i
=
ˆ
C C
i
i
+
2
-4-
中国科技论文在线
http://www.paper.edu.cn
假设生成一个随机数据所需的时间非常小，那么就可以认为获得 ˆ{ }iC 所需的时间应是
获得{ }iC 的时间的两倍。因此为了在相同的效率下，使用相反变量法要优于不使用方差缩
减技术的一般方法，应满足条件
ˆ
Var C
2
(
i
)
≤
Var C
(
i
)
。
我们可以很容易的证明该条件得以满足，定义函数
C
i
Zφ=
(
)
i
，其中 φ是股票价格关于
iZ 的函数同期权贴现值同 iZ 的函数的合成函数。作为两个单调增函数的合成函数，φ也是
单调增的。所以下面的不等式成立：
E
Z
[ (
) (
φ φ
(3-7)
[ (
φ
)]
)]
E
Z
−
≤
Z E
i
)] [ (
φ
−
Z
i
i
i
所以有
ˆ
COV C C
i
[
,
i
]
=
E
[ (
) (
φ φ
Z
i
−
Z
i
)]
−
E
[ (
φ
Z E
i
)] [ (
φ
−
Z
i
)] 0
≤ (3-8)
又因为
ˆˆ(
Var C
)
i
=
Var
[
ˆ
C C
i
i
+
2
]
=
1
2
Var C
(
i
[
]
+
所以
ˆ
Var C
2
(
i
)
≤
Var C
(
i
)
综上所述，相反变量法是一种简单有效的方差缩减方法。
4． 权证定价实例
4.1 参数估计
Cov C C
i
[
,
i
])
(3-9)
本文所研究的五粮 YGC1(030002)是以五粮液(000858)为标的物的百慕大式备兑认购权
证，发行于 2006 年 4 月 3 日，初始存续期为两年，最后交易日为 2008 年 3 月 26 日，行权
起始日为 2008 年 3 月 27 日，曾先后于 2006 年 6 月 6 日和 2007 年 5 月 9 日调整行权价格及
行权比例，其最新行权价格为 4.8980 元，最新行权比为 1：1.4020。
考虑到百慕大式权证的特点，将其近似看作到期日为 2008 年 3 月 27 日的欧式权证进
行研究，同时该权证的标的股五粮液(000858)曾先后于 2006 年 6 月 6 日和 2007 年 5 月 9 日
进行分红配股，在下面进行蒙特卡洛模拟时，对标的股价格进行除权除息。
选取 2006 年 6 月 7 日至 2008 年 2 月 5 日间的五粮液(000858)每个交易日的收盘价作为
资产历史价格数据。因为在该权证的存续期曾发生过一次行权价格的调整，因此所选择的时
间范围以五粮 YGC1(030002)行权价格调整日为分界点被分为两个阶段，对这两个阶段分别
使用蒙特卡洛模拟方法进行定价分析。时间划分如下：利用 06 年 6 月 7 日至 07 年 4 月 30
日的 214 个价格数据进行蒙特卡洛模拟，记为时间段 A；利用 07 年 5 月 8 日至 08 年 2 月 5
日的 187 个价格数据进行蒙特卡洛模拟，记为时间段 B。除此之外，再选取 07 年 8 月 6 日
至 08 年 2 月 5 日的 124 个价格数据进行蒙特卡洛模拟，记为时间段 C，作为对照组。数据
的选取确定下来后，开始进行参数的估计。
为了使用蒙特卡洛方法对五粮 YGC1(030002)进行定价，首先要确定模型中的各个参
数。现在利用其标的资产五粮液(000858)历史价格数据估计 µ和σ，公式如下：
µ
=
E
[ln(
S
t
i
+∆
t
∆
/
S
t
)]
-5-
(4-1)
中国科技论文在线
http://www.paper.edu.cn
2
σ
=
var[ln(
/
S
t
)]
S
t
i
+∆
t
∆
(4-2)
其中 t∆ 取为一天， t
首先用C++进行数据处理各时间段的价格历史数据，将其转化为资产价格对数收益率，
tS +∆ 、 tS 定义同公式（3-1）。
再利用SAS[7]
的统计功能计算各时间段对应的
E
[ln(
S
i
t
+∆
/
S
t
)]
及 var[ln(
S
i
t
+∆
/
S
t
)]
如下表：
表 4-1
E
[ln(
S
/
S
t
)]
及 var[ln(
S
i
t
+∆
/
S
t
)]
值
i
t
+∆
E
[ln(
S
i
t
+∆
/
S
t
)]
var[ln(
S
/
S
t
)]
i
t
+∆
0.005184212
0.002317197
0.001401945
0.001011130
0.001142914
0.001115310
进而由公式(4-1)及(4-2)
时间段
A
B
C
因为 t∆ 取为一天，我们设一年有 250 个交易日，则
计算得各时间段的参数 µ和σ的估计值如下表：
t∆ =
1/ 250
时间段
A
B
C
表 4-2 参数估计
µ
1.29605300
0.57929925
0.35048625
σ
0.2527825
0.2857285
0.2788275
现在来选取无风险利率，首先，在蒙特卡洛模型中，无风险利率被认为是固定的常数。
由于中国金融市场存在诸多不完善的地方，对于无风险利率很难准确估计，目前国内研究者
有采用定期存款利率、国债利率和银行间拆借利率作为无风险利率的估计。本文采用一年期
定期存款利率作为无风险利率。国内目前的一年期定期存款利率为 4.14%，扣除 20%的利息
税后实际利率为 3.312%，再转化为连续复利为 ln(1 0.0312) 0.032583
r =
+
=
4.2 蒙特卡洛模拟定价
下面基于时间段 A 进行蒙特卡洛模拟，考虑到每 10 股派 4 股并分 0.06 元的影响，故
(35.66 0.06) /1.4
元。利用 SAS 软件编写蒙特卡洛方法的程序，重复进行
25.43
−
≈
S =
0
10000 次模拟，将每隔 10 步所得到的一万个数据的均值导出，与对应时刻的五粮液(000858)
市场收盘价作比较，如下图：
）
元
（
格
价
80
70
60
50
40
30
20
10
0
1
15
30
45
实际价格
模拟价格
120
140
170
90
75
105
60
时间（日）
图 4-1 时间段 A 标的资产预测价格走势图
-6-
中国科技论文在线
http://www.paper.edu.cn
下面基于时间段 B 进行蒙特卡洛模拟， 0
S =
39.27
元。利用 SAS 软件编写蒙特卡洛方
法的程序，重复进行 10000 次模拟，将每隔 2 步所得到的一万个数据的均值导出，与对应时
刻的五粮液(000858)市场收盘价作比较，如下图：
）
元
（
格
价
45
40
35
30
25
20
15
10
5
0
实际价格
模拟价格
1
5
9
17
13
21
时间（日）
25
29
图 4-2 时间段 B 标的资产预测价格走势图
再将模拟得到的权证到期日的内在价值贴现至到期日之前存续期内，并与权证实际走
势进行比较，得下图：
）
元
（
格
价
60
50
40
30
20
10
0
实际价格
模拟价格
1
3
5
7
9
11
13
15
时间（日）
图 4-3 时间段 B 权证预测价格走势图
下面基于时间段 C 进行蒙特卡洛模拟， 0
S =
39.27
元。利用 SAS 软件编写蒙特卡洛方
法的程序，重复进行 10000 次模拟，将每隔 2 步所得到的一万个数据的均值导出，与对应时
刻的五粮液(000858)市场收盘价作比较，如下图：
）
元
（
格
价
45
40
35
30
25
20
15
10
5
0
1
5
9
17
21
13
时间（日）
25
29
-7-
实际价格
模拟价格
中国科技论文在线
http://www.paper.edu.cn
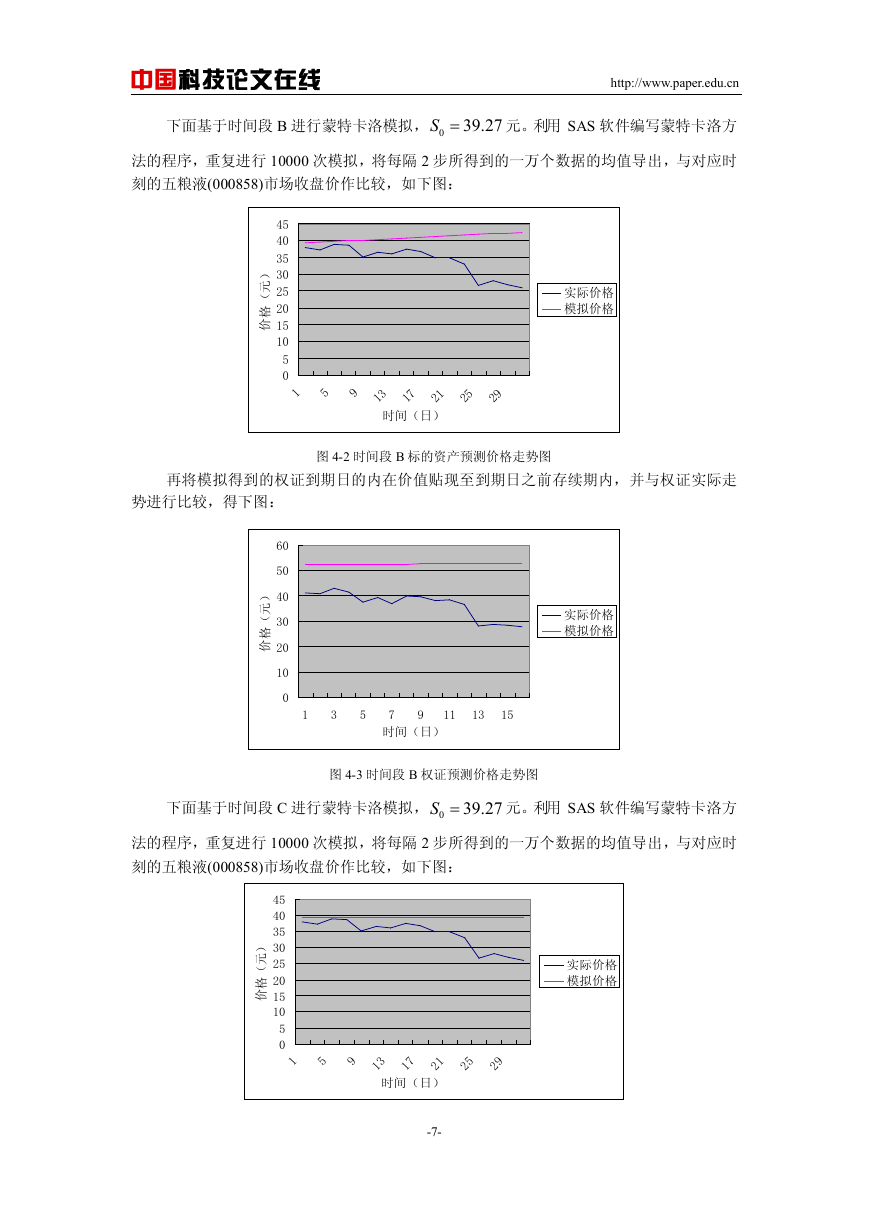
再将模拟得到的权证到期日的内在价值贴现到到期日之前存续期内，并与权证实际走
图 4-4 时间段 C 标的资产预测价格走势图
势进行比较，得下图：
）
元
（
格
价
60
50
40
30
20
10
0
实际价格
模拟价格
1
5
9
17
21
13
时间（日）
25
29
图 4-5 时间段 C 权证预测价格走势图
对三个时间段进行蒙特卡洛模拟得标的资产在到期日终值以及相应的权证到期价值
（行权价为 4.8980，行权比为 1：1.402）如下表：
表 4-3 蒙特卡洛模拟价格与实际价格对照
权证预测
价值
权证实际
价值
27.749
27.749
27.749
时间段
资产到期日
模拟价格
82.61547
42.47585
39.27706
资产实际
价格
25.92
25.92
25.92
108.804458
52.6841457
48.1994421
A
B
C
对比标的资产价格走势图以及表 3-3 中的数据可以看出，基于 近期数据估计参数 µ和σ
所形成的蒙特卡洛模型预测精度较基于远期数据估计参数 µ和σ所形成的蒙特卡洛模型的
预测精度高。比较时间段 B、C 的预测结果亦能发现，在进行中、短期预测时，历史数据选
取范围不宜过大，要根据剩余的存续期来决定历史数据的选取范围。而表 4-2 中不同时间段
的σ没有太大差异，因此可以认为在蒙特卡洛模型中参数 µ起决定性作用。同时通过观察
时间段 A 的标的资产预测价格走势图的前半部分不难发现蒙特卡洛模型具有很强的趋势性，
因为估算出参数 µ后即为一常数，故该模型不能好好的预测出与历史数据整体走势相违的
价格变动，也就是说该模型适用于中、短期的权证定价。最后时间段 B、C 的权证价格走势
图表明，利用一般的蒙特卡洛模拟方法对权证进行定价，对投资者制定合理的投资决策无积
极的影响，因为根据蒙特卡洛模型得出的权证理论价格与实际权证价格走势相违。
4.3 利用指数加权移动平均模型改进蒙特卡洛模型
已知参数 µ的估计公式如下：
=
µ
E
[ln(
S
t
i
+∆
t
∆
/
S
t
)]
(4-3)
即不管数据是远期的还是近期的都同等看待，或者说是等权重的，但有上一节的结果可
以看出基于近期的数据进行定价要比基于远期数据进行定价精确，也就是说近期的数据对预
测影响较远期的要大，因此为了更精确地估计参数 µ，我们采取指数加权平均模型进行估
算，具体公式如下：
µ
t
=
1
∆ ∑
t
1
=
n
k
k
λ
w
R
t k
−
(4-4)
-8-
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
