蚁群算法在GIS中的应用.pdf-资料库

weixin_38684328-12159143-4744300845386796770.pdf-第1页.png

第1页 / 共7页

weixin_38684328-12159143-4744300845386796770.pdf-第2页.png

第2页 / 共7页

weixin_38684328-12159143-4744300845386796770.pdf-第3页.png

第3页 / 共7页

weixin_38684328-12159143-4744300845386796770.pdf-第4页.png

第4页 / 共7页

weixin_38684328-12159143-4744300845386796770.pdf-第5页.png

第5页 / 共7页

weixin_38684328-12159143-4744300845386796770.pdf-第6页.png

第6页 / 共7页

weixin_38684328-12159143-4744300845386796770.pdf-第7页.png

第7页 / 共7页

http://www.paper.edu.cn 蚁群算法在 GIS 中的应用王诚辽宁工程技术大学测绘与地理科学学院，辽宁阜新（123000） E-mail：cheng3570@163.com 摘要：蚁群算法是由意大利学者Dorigo等人于20世纪90年代初期通过模拟自然界中蚂蚁集体寻径的行为而提出的一种基于种群的启发式仿生进化系统。本文用蚁群算法的出现及其不断的发展和完善，为最短路径的求解提供了一种新的有效的方法。本文将对该算法应用于 GIS中最短路径的求解方面的问题进行初步的研究。并且该算法采用了分布式正反馈并行计算机制,易于与其他方法结合,而且具有较强的鲁棒性,是一种很有前途的仿生优化算法。本文将对该算法应用于GIS中最短路径的求解方面的问题进行初步的研究。关键词：蚁群算法；应用研究 1. 前言蚁群算法( ant colony algorithm) 是由意大利学者 Dorigo 等人于20世纪90年代初期通过模拟自然界中蚂蚁集体寻径的行为而提出的一种基于种群的启发式仿生进化系统。蚁群算法包含两个基本阶段:适应阶段和协作阶段。在适应阶段,各候选解根据积累的信息不断调整自身结构。在协作阶段,候选解之间通过信息交流,以期望产生性能更好的解,这类似于学习自动机的学习机制。蚁群算法最早成功应用于解决著名的旅行商问题(traveling salesman problem , TSP) ,该算法采用了分布式正反馈并行计算机制,易于与其他方法结合,而且具有较强的鲁棒性。随着计算机软硬件技术的飞速进步,地理信息系统得到了快速的发展。网络分析作为地理信息系统(GIS)最主要的功能之一,在导航、交通、旅游、城市规划以及电力、通讯等各个方面中发挥了重要的作用。网络分析要解决的问题中有两个是和最短路径相关的。一个是最佳路径选择，比如由A地前往B地，选择怎样的路线才是最佳的。另一个是资源分配的问题，它是关于资源调送的问题，广泛应用于消防站点分布，选址，物资分配，供水供电等方面。最短路径不仅仅指一般地理意义上的距离最短,还包括其他的方面,如最短的时间、最少的费用等。所以，最短路径问题其实是最佳路径问题、最低费用等的问题[1]。传统的最短路径求解算法-Dijkstra算法是目前多数系统解决最短路径问题采用的理论基础,它的各种该进算法得到了广泛的应用。而蚁群算法的出现及其不断的发展和完善，为最短路径的求解提供了一种新的有效的方法。本文将对该算法应用于GIS中最短路径的求解方面的问题进行初步的研究。蚁群算法采用了分布式正反馈并行计算机制,易于与其他方法结合,而且具有较强的鲁棒性,是一种很有前途的仿生优化算法。本文将对该算法应用于GIS中最短路径的求解方面的问题进行初步的研究。 2. 蚁群算法及其原理 2.1 蚁群算法介绍蚁群算法创立十多年来,无论在算法理论还是在算法应用方面都取得了很多突破性研究进展。作为一个前沿性的热点研究领域,蚁群算法已引起越来越多国内外研究者的关注,近五年内其研究人员和研究成果均成几何级数增长。其应用范围几乎涉及到各个优化领域,而且还出现了蚁群算法仿生硬件,可见这种新兴的仿生优化算法已经显示出强大的生命力和广阔的发展前景。尽管人们对蚁群算法的研究时间不长,在这一领域还有一些问题需要进一步研 - 1 -

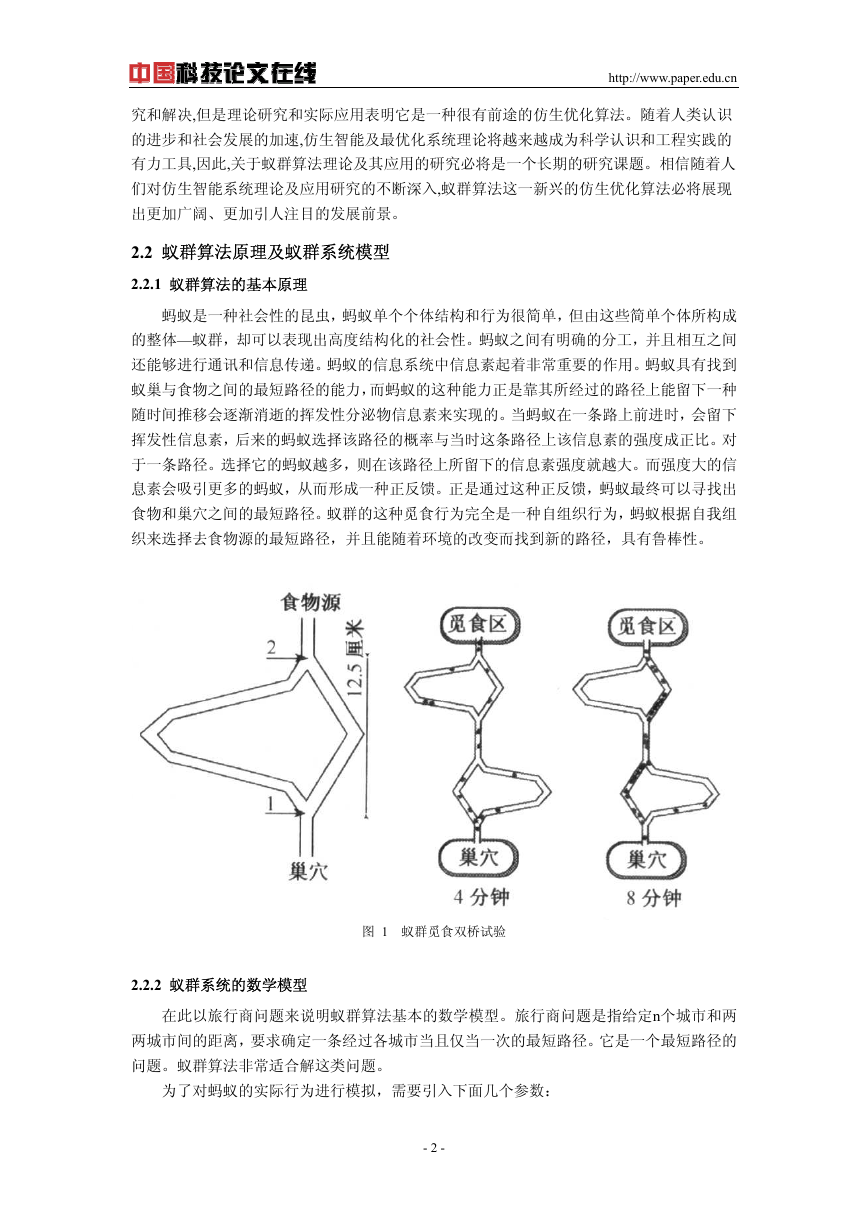
http://www.paper.edu.cn 究和解决,但是理论研究和实际应用表明它是一种很有前途的仿生优化算法。随着人类认识的进步和社会发展的加速,仿生智能及最优化系统理论将越来越成为科学认识和工程实践的有力工具,因此,关于蚁群算法理论及其应用的研究必将是一个长期的研究课题。相信随着人们对仿生智能系统理论及应用研究的不断深入,蚁群算法这一新兴的仿生优化算法必将展现出更加广阔、更加引人注目的发展前景。 2.2 蚁群算法原理及蚁群系统模型 2.2.1 蚁群算法的基本原理蚂蚁是一种社会性的昆虫，蚂蚁单个个体结构和行为很简单，但由这些简单个体所构成的整体—蚁群，却可以表现出高度结构化的社会性。蚂蚁之间有明确的分工，并且相互之间还能够进行通讯和信息传递。蚂蚁的信息系统中信息素起着非常重要的作用。蚂蚁具有找到蚁巢与食物之间的最短路径的能力，而蚂蚁的这种能力正是靠其所经过的路径上能留下一种随时间推移会逐渐消逝的挥发性分泌物信息素来实现的。当蚂蚁在一条路上前进时，会留下挥发性信息素，后来的蚂蚁选择该路径的概率与当时这条路径上该信息素的强度成正比。对于一条路径。选择它的蚂蚁越多，则在该路径上所留下的信息素强度就越大。而强度大的信息素会吸引更多的蚂蚁，从而形成一种正反馈。正是通过这种正反馈，蚂蚁最终可以寻找出食物和巢穴之间的最短路径。蚁群的这种觅食行为完全是一种自组织行为，蚂蚁根据自我组织来选择去食物源的最短路径，并且能随着环境的改变而找到新的路径，具有鲁棒性。图 1 蚁群觅食双桥试验 2.2.2 蚁群系统的数学模型在此以旅行商问题来说明蚁群算法基本的数学模型。旅行商问题是指给定n个城市和两两城市间的距离，要求确定一条经过各城市当且仅当一次的最短路径。它是一个最短路径的问题。蚁群算法非常适合解这类问题。为了对蚂蚁的实际行为进行模拟，需要引入下面几个参数： - 2 -

http://www.paper.edu.cn m：蚁群中蚂蚁的数量 )(tbi ：t时刻位于城市i的蚂蚁个数 ijd ：两城市i和j之间的距离 ijη ：边（i，j）的能见度，反映由城市i转移到城市就，启发程度，这个量在运行中不改变 ijτ ：边（i，j）上的信息素强度 ijτ∆ ：蚂蚁k在边（i，j）上留下的单位长度轨迹信息素量 ijP ：蚂蚁k的转移概率，j是尚未访问的城市 k 其中， m = ∑ 人工模拟的单个蚂蚁具有如下的行为特征：（1）移动过程中会在边（i，j）上释放信息素（2）单个蚂蚁概率的选择下一个城市，这个概率是由两城市间的距离和边上信息素（2.1） i tb )( 1 = n i 的数量的函数来决定的（3）在一次循环内，单个蚂蚁不可重复访问同一个城市蚂蚁的转移概率由下式给出： tP )( k ij t t )( )( β α ητ ij ij t t )( )( α β ητ is is k ⎧ ⎪⎪ = ∑ ⎨ s allowed ∈ ⎪ otherwise ,0 ⎪ ⎩ , j ∈ allowed k （2.2）其中， allowed 为可选的城市列表。为了使不重复的经过所有城市，每只蚂蚁都有一 k 张禁忌表。它记录了蚂蚁已经走过的城市。当一次循环结束后，禁忌表用来计算该蚂蚁当前所建立的解决方案。之后该表被清空。信息素修正规则由下式给出： )1 =+ t ( τ ij . τρ ij ∆ τ ij tt ,( + )1 = ∆+ τ ij tt ,( + )1 （2.3） k ∆ τ ij tt ,( + )1 （2.4） t )( m ∑ k 1 = ttk ,( 1 其中， + ∆ ijτ ）表示本次循环中路径（i，j）的信息素增量；）表示第k只蚂蚁在时刻（t，t+1）留在路径（i，j）上的信息素量。 1( ρ− 为信息素衰减系数，通常 ) 1 tt ,( + ∆ ijτ 小于一，以避免路径上信息素量无限增加。简单蚁群算法流程图如下： - 3 -

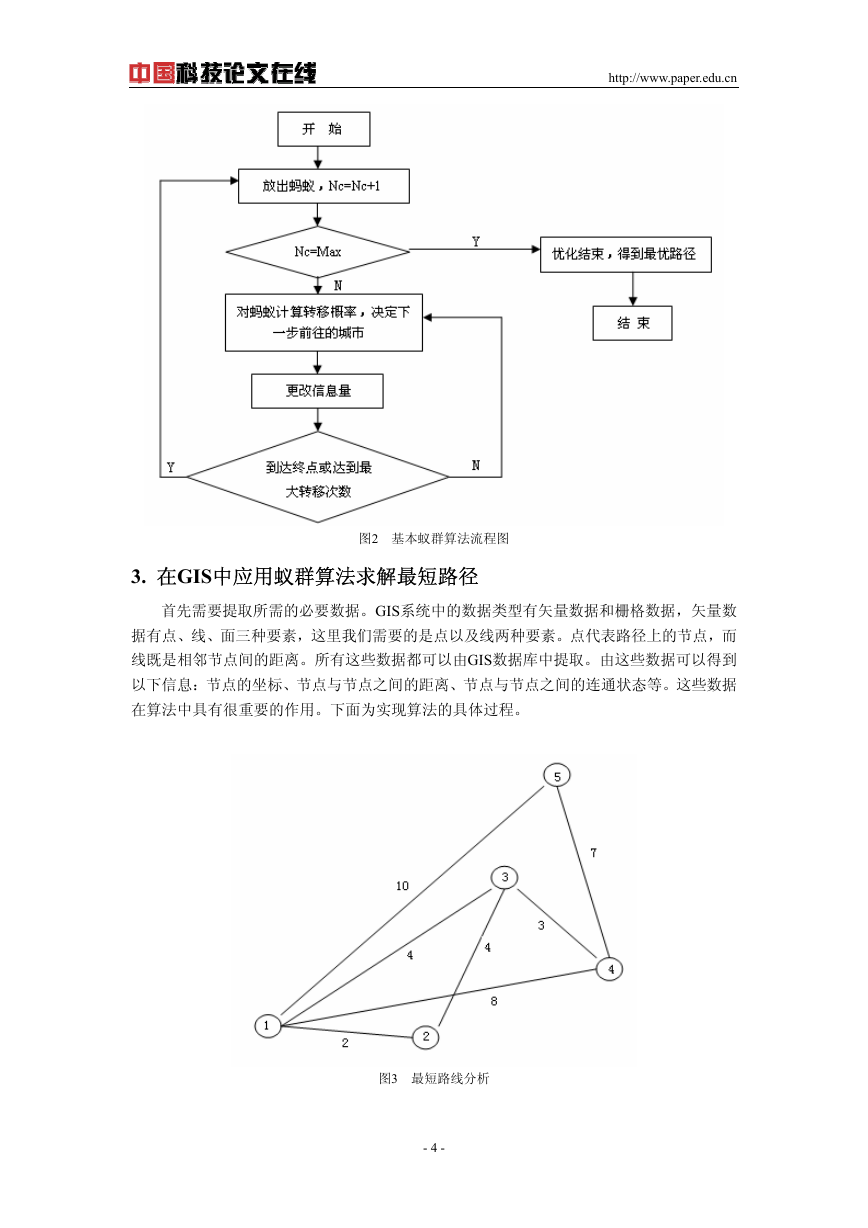
http://www.paper.edu.cn 3. 在GIS中应用蚁群算法求解最短路径图2 基本蚁群算法流程图首先需要提取所需的必要数据。GIS系统中的数据类型有矢量数据和栅格数据，矢量数据有点、线、面三种要素，这里我们需要的是点以及线两种要素。点代表路径上的节点，而线既是相邻节点间的距离。所有这些数据都可以由GIS数据库中提取。由这些数据可以得到以下信息：节点的坐标、节点与节点之间的距离、节点与节点之间的连通状态等。这些数据在算法中具有很重要的作用。下面为实现算法的具体过程。图3 最短路线分析 - 4 -

上图为节点1和4之间的连通情况及节点间的路线长度。要用蚁群算法选择1至4两节点之间的最短路径。可选路径所满足的条件为：①两节点之必须存在路径；②一次循环中，同一节点最多只能经过一次。第一个条件可用一个节点间的连通矩阵来控制，节点间相通用节点间虚拟路径长度来表示，不连通用0表示，如下表所示： http://www.paper.edu.cn 1 2 3 4 5 1 0 2 4 8 10 表1 节点连通情况 2 3 4 2 4 0 4 0 3 0 0 0 4 8 0 3 0 7 5 10 0 0 7 0 该表可采用二维数组来存储，为了节省存储空间也可采用一维数组，但是为获取节点连通情况需要进行一些计算，而不是直接查询。该表只存在一张，供所有蚂蚁查询，其内容是不变的。虚拟路径长度是根据现实情况提出的。现实情况是在路径长度相同时，有一地前往另一地的时间还会受到路况、交通量、天气等各种要素的影响，因此需要把真实路径长度乘上一个系数来模拟实际的情况。第二个条件由禁忌表控制。每只蚂蚁都有自己的一张禁忌表。禁忌表可由一个一维数组表示，表的初始值为0，表长度为节点数。它记录的是蚂蚁的前进路径，并能防止重复经过同一节点。表2 蚂蚁i的禁忌表 1 2 3 4 0 该表表示蚂蚁i经过 1，2，3，4 这条路径，即这是连通节点1和4的一条路径。这样每只蚂蚁的行为规则如下：（1）根据禁忌表和连通表确定可选的下一个节点，由转移概率公式确定到底前往那一个节点；（2）前往下一个节点后更新禁忌表，如果还没有到达节点4，回到第一步。到达节点4 后，该循环结束，然后根据公式（2.3）进行信息素的修正，然后进入下一循环，直到找到较满意的最优解。算法中的初始参数要通过实验的方法进行选取。在寻求最优解的的过程中，蚂蚁可能进入一个无法到达节点4的路径，从而找不到一条到达节点4的路径从而无法完成循环，如下图所示： - 5 -

http://www.paper.edu.cn 图4 蚂蚁无法完成一次循环的情况蚂蚁进入5—6—7这条路径并到达节点7后，如果按照上面的行为规则，该蚂蚁就永远也无法完成一次循环，因此需要修正，加入下面第三条：（3）蚂蚁具有识别如上图所示的情况。对它的处理是将节点5和6之间的虚拟路径长度修改为零，强制结束该循环，重置禁忌表，并且不进行信息素的修正而直接进入下一循环。 4. 结论蚁群算法由于出现的时间相对来说比较短，还存在如下不足： (1)限于局部最优解． (2)工作过程的中间停滞问题． (3)较长的搜索时间．针对这些问题，各种蚁群算法的改进算法不断出现，比如带精英策略的蚁群系统、基于优化排序的蚁群系统、最大最小蚁群系统、最优最差蚁群系统等[2]。其性能在不断的提高，适用范围也在不断扩大。随着研究的继续深入，它一定会发展为一种很高效的优化算法，成为GIS应用中的一个强有力的工具。参考文献 [1] 黎夏,刘凯,《GIS与空间分析—原理与方法》[M].北京:科学出版社,2006.8. [2] 李士勇,陈永强,李研.《蚁群算法及其应用》[M].哈尔滨:哈尔滨工业大学出版社,2004.9. - 6 -

http://www.paper.edu.cn The ant group algorithm hits the target in GIS applying School of Geomatic, Liaoning Technical University, Fuxin, Liaoning (123000) Wang Cheng Abstract Ant alogrithm is form Ttaly and schoolars Dorigo, who in the early 1990s through the simulation of the collective nature of the ants and roulting of the propulation based on a heurisic bionic evolution system. In this paper, ant algorithm and the emergence of continuous devolopment and improvent of the shortest path to the solution provides a new and effective methods. This paper will be applied to the algorithm in GPS shortest path to solve the problem of conducting a preliminary study. The algorithn used and distributed parralled computer system of positive feedbacl and easy to integrate with other methods, but also is robust, is a promising bionic optimization algorithm. This paper will be applied to the algorithms, Preliminary Study. Keywords: Ant Colony Algorithms; Preliminary Study - 7 -

资料库

蚁群算法在GIS中的应用.pdf

相关推荐

开发技术

热门标签

最新资料