guaranteeing secrecy using artificial noise.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：0.43M 资料格式：pdf 举报版权申诉

u014446839-8535641-4744302542855438165.pdf-第1页.png

第1页 / 共10页

u014446839-8535641-4744302542855438165.pdf-第2页.png

第2页 / 共10页

u014446839-8535641-4744302542855438165.pdf-第3页.png

第3页 / 共10页

u014446839-8535641-4744302542855438165.pdf-第4页.png

第4页 / 共10页

u014446839-8535641-4744302542855438165.pdf-第5页.png

第5页 / 共10页

u014446839-8535641-4744302542855438165.pdf-第6页.png

第6页 / 共10页

u014446839-8535641-4744302542855438165.pdf-第7页.png

第7页 / 共10页

u014446839-8535641-4744302542855438165.pdf-第8页.png

第8页 / 共10页

文本预览

2180 IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 7, NO. 6, JUNE 2008 Guaranteeing Secrecy using Artiﬁcial Noise Satashu Goel, Student Member, IEEE, and Rohit Negi, Member, IEEE Abstract—The broadcast nature of the wireless medium makes the communication over this medium vulnerable to eavesdrop- ping. This paper considers the problem of secret communication between two nodes, over a fading wireless medium, in the presence of a passive eavesdropper. The assumption used is that the transmitter and its helpers (amplifying relays) have more antennas than the eavesdropper. The transmitter ensures secrecy of communication by utilizing some of the available power to produce ‘artiﬁcial noise’, such that only the eavesdropper’s channel is degraded. Two scenarios are considered, one where the transmitter has multiple transmit antennas, and the other where amplifying relays simulate the effect of multiple antennas. The channel state information (CSI) is assumed to be publicly known, and hence, the secrecy of communication is independent of the secrecy of CSI. Index Terms—Privacy, secrecy capacity, wireless. I. INTRODUCTION W IRELESS networks have gained much popularity be- cause of the broadcast nature of the wireless medium, which makes it easily accessible. However, this ease of ac- cessibility also makes it easy to overhear communication over this medium, thus raising privacy concerns. Secrecy problems involve three nodes; transmitter, receiver and an eavesdropper. We consider the problem of secret communication from the transmitter to the receiver, over a wireless medium, where a passive eavesdropper may be present. The transmitter wants to transmit a secret message to the intended receiver, such that the eavesdropper is unable to decode it. The eavesdropper is assumed to be passive and hence, its location, and even its presence will be uncertain to the transmitter. Any scheme that guarantees secrecy in such a scenario, must do so regardless of the eavesdropper’s position. Claude Shannon laid the theoretical foundation for the study of secret communication [1]. He showed that perfect secrecy is achievable only if the secret key is at least as large as the secret message. However, this pessimistic result was based on the assumption that the eavesdropper has access to precisely the same information as the receiver, except the secret key. Later, [2] considered a scenario where the receiver and the eavesdropper have separate channels, and showed that secret communication is possible if the eavesdropper’s channel has a smaller capacity than the receiver’s channel. Manuscript received October 18, 2006; revised May 4, 2007, October 23, 2007, and April 20, 2008; accepted March 19, 2008. The associate editor coordinating the review of this paper and approving it for publication was A. Gulliver. This work was supported in part by Cylab, CMU under grant DAAD19-02-1-0389 from the Army Research Ofﬁce. Part of the results in this paper have been presented in VTC Fall ’05 and MILCOM ’05. S. Goel is pursuing his Ph.D. at the Department of Electrical and Computer Engineering, Carnegie Mellon University (e-mail: satashug@ece.cmu.edu). R. Negi is an Associate Professor at the Department of Electrical and Com- puter Engineering, Carnegie Mellon University (e-mail: negi@ece.cmu.edu). Digital Object Identiﬁer 10.1109/TWC.2008.060848. 1536-1276/08$25.00 c 2008 IEEE The paper generalized the scenario considered in [3] where the eavesdropper’s channel was a degraded version of the re- ceiver’s channel. The paper also deﬁned the notion of ‘secrecy capacity’, which essentially is the maximum rate at which the transmitter can reliably communicate a secret message to the intended receiver, without the eavesdropper being able to decode it. However, if the eavesdropper happens to have a better channel than the receiver (e.g., if the eavesdropper is closer to the transmitter, versus the receiver), then the secrecy capacity is zero, meaning that secrecy cannot be guaranteed. This paper presents a solution to this problem, where the transmitter can use some of the available power to transmit artiﬁcially generated noise. Since, this noise is generated by the transmitter, the transmitter can design it such that only the eavesdropper’s channel is degraded. Thus, by selectively degrading the eavesdropper’s channel, secret communication can be guaranteed, based on the result in [2]. Two schemes for generating artiﬁcial noise were presented in [5]. In the ﬁrst scheme, the transmitter can use multiple transmit antennas to generate ‘artiﬁcial noise’. This scenario was chosen because the artiﬁcial noise scheme can be pre- sented in a simple manner, in this case. This scenario models a base station wanting to communicate a secret message to a mobile handset. In the second scheme, it was shown that even if the transmitter does not have multiple transmit antennas but ‘amplifying relays’ [20] (or ‘helper nodes’) are present, the effect of multiple antennas can be simulated and artiﬁcial noise can still be produced. This scenario models a mobile handset, with a single antenna, wanting to communicate a secret message to another mobile handset or the base station. The multiple antenna scheme was further analyzed in [6]. The paper explored the notion of ‘MIMO secrecy capacity’ and showed that it behaves differently from MIMO capacity, showing that the secrecy requirement changes the behavior of MIMO capacity. For example, the paper showed that secrecy capacity does not increase monotonically with the minimum of the number of transmit and receive antennas, unlike the celebrated result on usual MIMO capacity [7]. Thus, the paper highlighted the need to characterize MIMO secrecy capacity. The paper further showed that with the use of artiﬁcial noise, a certain minimum rate of secret transmission can be guaranteed, regardless of the eavesdropper’s position. In this paper, we present results on the minimum secrecy capacity, that can be guaranteed regardless of the eavesdropper’s position, called minimum guaranteed secrecy capacity, assuming a fading channel model. This requires a modiﬁcation of the schemes analyzed in [5] and [6] to guarantee non-zero secrecy capacity. Note that the result in [2], and consequently, this paper, con- siders information theoretic secrecy which is provably secure, as opposed to classical symmetric encryption schemes [4].

GOEL and NEGI: GUARANTEEING SECRECY USING ARTIFICIAL NOISE Information theoretic secrecy does not assume that a secure key exchange has occurred between the transmitter and the receiver, as is assumed in the classical symmetric encryption schemes. On the other hand, the secrecy rates guaranteed by the information theoretic results might be substantially smaller than those achievable through symmetric encryption schemes. Thus, information theoretic schemes can be used in conjunction with the classical schemes, by generating keys which can then be used to perform symmetric encryption. However, practical codes are not known which can achieve the rates guaranteed by information theoretic results on secrecy. In related work, [8] presented a technique for introducing ambiguity in the eavesdropper’s channel, using multiple trans- mit antennas. However, secrecy capacity obtained using this scheme was not analyzed. [9] described a technique for secret communication where the channel state information (CSI) was used as the secret key. In particular, the phase information was used as a secret key and the transmitter compensated for the phase before transmission. The phase of the eavesdropper’s channel, being different from that of the receiver’s channel, in general, prevented the eavesdropper from decoding the secret message. [10] generalized this technique for the multi-antenna scenario. [11] obtained an abstract characterization of secrecy capacity of the kind discussed in [9]. In contrast, this paper assumes that the CSI is publicly known, and thus, it cannot be used to obtain a secret key. The secrecy of the schemes discussed in this paper is independent of the secrecy of CSI. However, here we make the (admittedly strong) assumption that the number of eavesdropper antennas is strictly smaller than the number of transmitter (along with amplifying relays) antennas. This assumption may be valid in certain scenarios, such as a powerful base station deploying several antennas, serving as a transmitter. [12] presented an analytical solution for the multi-antenna scenario, assuming that the eavesdrop- per’s channel is known to the transmitter. [13] analyzed secrecy capacity for slow fading wireless channels, but without the use of artiﬁcial noise. This paper shows that much lower outage probabilities can be guaranteed using artiﬁcial noise. The paper is organized as follows. Section II formulates the secrecy problem considered in this paper. It introduces the two scenarios considered here, one with multiple antennas at the transmitter, and the other with amplifying relays. Section III introduces the scheme for artiﬁcial noise generation, using multiple transmit antennas. This section assumes that both the receiver and the eavesdropper have a single antenna each. Section IV presents the scheme for artiﬁcial noise generation, when all the nodes have a single antenna each. This section shows how the effect of multiple transmit antennas can be reproduced with the help of amplifying relays. Section V characterizes the behavior of MIMO secrecy capacity. It also presents analytic results in the regime of large number of antennas. Section VI presents simulation results and their discussion. Section VII concludes the paper. II. PROBLEM SCENARIO We denote vectors and matrices with bold font, and the Hermitian operator by †. For convenience, we measure infor- mation in nats instead of bits (i.e., loge(·) is used to calculate NR N T H A N E G B E αAH 1 α H E1 αAHN A αAE 2181 α AB H 1 α H B1 α BH1 αBHN α H BN H E N B BEα H N α E (a) Scenario 1 (b) Scenario 2 Fig. 1. Framework for secrecy capacity. entropy). We consider two scenarios, which demonstrate dif- ferent methods of generating artiﬁcial noise. In the multiple amplifying relays scenario, we assume that transmissions of all nodes are synchronized (which is clearly an idealistic assump- tion). The key idea in this paper is that a transmitter, perhaps in cooperation with the amplifying relays, can generate noise artiﬁcially to conceal the secret message that it is transmitting. i.e., the transmitter can use some of the available power to transmit artiﬁcially generated noise, to selectively degrade eavesdropper’s channel. A. Multiple Antennas: Scenario 1 Scenario 1 in Fig. 1 shows transmitter A with NT antennas, receiver B with NR antennas and an eavesdropper E with NE antennas. An eavesdropper with multiple antennas is an abstraction of the case where, a) either the eavesdropper has multiple receive antennas or b) several eavesdroppers (with perhaps one antenna each) collude. The latter case of collusion can be modeled as a single eavesdropper with multiple antennas, if we assume that their received signals can be processed by a central node. Clearly, this form of collusion represents the worst case scenario in terms of secrecy capacity, given a ﬁxed number of colluding eavesdroppers. Hk and Gk denote the channels of the receiver and the eavesdropper respectively, at time k. The elements of Hk (Gk), denoted by hi,j (gi,j), is the channel gains from transmit antenna i to receive (eavesdropper) antenna j. A transmits xk at time k. B and E receive, respectively, zk = Hkxk + nk, yk = Gkxk + ek, (1) (2) where the components of nk and ek are i.i.d. Additive White Gaussian Noise (AWGN) samples with variance σ2 n and σ2 e, respectively. Block fading is assumed, meaning that Hk and Gk are constant over a block of large number of symbols so that information theoretic results can be applied within each block and Hk, Gk in different blocks are independent. Encoding and decoding is performed independently for each fading block. A more general fading channel could be used, but the resulting analysis will be much more complicated [21]. hi,j and gi,j are assumed to be complex numbers, i.i.d. and independent of each other. This would occur under ‘rich

2182 IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 7, NO. 6, JUNE 2008 it scattering’ [14]. It is assumed that the receiver is able to estimate its channel Hk perfectly and feed it back to the transmitter noiselessly. We assume that Hk is communicated to the transmitter by an authenticated broadcast (which may be heard by the eavesdropper). Thus, is assumed that the eavesdropper may know both the receiver’s and its own channel. A passive eavesdropper is assumed, which means that it only listens but does not transmit. Hence, its channel Gk may not be known to the transmitter. Note that the secrecy of this scheme is not dependent on the secrecy of channel gains. The transmitter is assumed to have a power constraint of xk] ≤ P0. Let the secret message mK .= i.e., E[x† P0, (m1, . . . , mK) be encoded into xN . zN and yN are then obtained following (1), (2). The rate of transmission between the transmitter and the receiver is R = H(mK)/N . The secrecy condition is deﬁned in terms of equivocation rate, K H(mK|yN ). Perfect secrecy is achieved deﬁned as Re (as deﬁned in [2]) if Re = R. Note that this secrecy condition restricts the rate at which the eavesdropper can obtain the secret information. A stricter secrecy condition can be used which restricts the total amount of secret information obtained by the eavesdropper, using the techniques introduced in [19]. .= 1 k B. Multiple Amplifying Relays: Scenario 2 In the previous scenario, the transmitter could utilize its multiple transmit antennas for secret transmission. This sce- nario considers the case where the transmitter does not have multiple transmit antennas, but instead, has amplifying relays for cooperation. Henceforth, in this paper, we will refer to them as relays. Scenario 2 in Fig. 1 shows transmitter A, intended receiver B and an eavesdropper E with only a single antenna each. But several relays (H1, H2, . . . , HN ) exist to aid secret communication from A to B. The multiple relays must simulate the effect of having multiple transmit antennas. However, unlike Scenario 1, the transmitter cannot directly control the signal transmitted by the relays. The channel gain from X to Y is denoted αXY , which models a fading channel. Note that the channels are not necessarily reciprocal, i.e., in general αXY = αY X. A frequency ﬂat block fading channel model is assumed, similar to (1), (2). The transmission of secret information from the transmitter to the receiver occurs in two stages which will be discussed in detail in a later section. It is assumed that all the channel gains are known to all the nodes (possibly, even to the eavesdropper). Again, the secrecy of our communication scheme does not depend on the secrecy of channel gains. We assume that the total power transmitted by all the nodes for both the stages (including nodes A, B and the relays), is constrained to P0. III. ARTIFICIAL NOISE USING TRANSMIT ANTENNAS In this section, we consider Scenario 1. This section as- sumes that both the receiver and the eavesdropper have a single antenna each, and that multiple eavesdroppers cannot collude (i.e., NR = NE = 1). An example of such a scenario is a wireless LAN, with the base station as the transmitter. The concept of artiﬁcial noise can be clearly illustrated in this scenario. The artiﬁcial noise is produced such that it lies in the , while the information signal is transmitted in the range space of the receiver’s channel. This design relies on knowledge of the receiver’s channel, but not of the eavesdropper’s channel. The receiver’s channel nulls out the artiﬁcial noise, and hence, the receiver is not affected by the noise. However, in general, the eavesdropper’s channel will be degraded, since its range space will be different from that of the receiver’s channel, and hence, some component of artiﬁcial noise will lie in its range space. We now describe how the transmitter can generate artiﬁcial noise to degrade the eavesdropper’s channel. The transmitter chooses xk as the sum of information bearing signal sk and the artiﬁcial noise signal wk, xk = sk + wk. (3) Both sk and wk are assumed complex Gaussian vectors. wk is chosen to lie in the null space of Hk, such that Hkwk = 0. If Zk is an orthonormal basis for the null space of Hk, then wk = Zkvk, and Z† Zk = I. Then, the signals received by the receiver and the eavesdropper are given by, respectively, k zk = Hksk + nk, yk = Gksk + Gkwk + ek. (4) (5) Note how the artiﬁcial noise wk is nulled out by the receiver’s channel but not necessarily by the eavesdropper’s channel. Thus, the eavesdropper’s channel is degraded with high prob- ability, while that of the receiver remains unaffected. If wk was chosen ﬁxed, the artiﬁcial noise seen by the eavesdropper would be small if Gkwk is small. To avoid this possibility, the sequence of wk is chosen to be complex Gaussian random vectors in the null space of Hk. In particular, the transmitter chooses elements of vk to be i.i.d. complex Gaussian random variables with variance σ2 v, and independent in time as well. It follows that the elements of wk are also Gaussian distributed. Since Hk is a vector channel, the transmitter chooses the information bearing signal as sk = pkuk, where uk is the information signal. We assume that Gaussian codes are used. pk is chosen such that Hkpk = 0 and pk = 1. Now, secrecy capacity is bounded below by the difference in mutual information between the transmitter and the receiver versus the transmitter and the eavesdropper [2], [15], |Hkpk|2σ2 u )−log(1+ |Gkpk|2σ2 Secrecy Capacity ≥ Ca sec = I(Z; U) − I(Y ; U) E|Gkwk|2 + σ2 ), where E|Gkwk|2 = (GkZkZ† v. For a passive eaves- dropper, Gk is not known to the transmitter, so using the con- cavity of log(·) and the i.i.d. assumption of Hk, the average k/Hk. secrecy capacity is maximized by choosing pk = H† Thus, the information bearing signal sk lies in the range space k whereas the artiﬁcial noise lies in the null space of H† of H† k. Ca is a function of sec is a random variable because it random channel gains Hk and Gk. Therefore, we study average secrecy capacity and outage probability (or outage capacity). We assume that the total transmit power, given by f1(σ2 v, is constrained to P0. Now, σ2 v can be chosen to maximize the lower bound on average secrecy capacity, u + (NT − 1)σ2 xk] ≤ P0 = σ2 v) = E[x† G† k)σ2 k = log(1+ (6) (7) u e σ2 n u, σ2 k u, σ2 Ca sec .= max u,σ2 v )≤P0 f1(σ2 E Hk,Gk [Ca sec]. (8)

GOEL and NEGI: GUARANTEEING SECRECY USING ARTIFICIAL NOISE 2183 u, σ2 sec involves both the expectation Note that the deﬁnition of Ca over Hk, Gk, and optimization over σ2 v. Similar notation will be used in the later sections to denote maximum average sec with the secrecy capacity. We now study the variation of Ca eavesdropper’s distance from the transmitter. For simpliﬁca- tion, (5) is normalized by a factor of Gk. Thus, the distance can be modeled as position dependent noise power σ2 e , instead of position dependent channel gains. The worst case situation → 0 (e.g., when the eavesdropper is would occur if σ2 e much closer to the transmitter, compared to the receiver). The minimum secrecy capacity that can be guaranteed, irrespective of the eavesdropper’s position is given by, Hk2σ2 u ) σ2 n ≥ Ca sec,mg .= Ca sec f1(σ2 max v )≤P0 u,σ2 − log(1+ Hk,Gk E [log(1+ |Gkpk|2σ2 G† u )]. (9) v k k)σ2 (GkZkZ† Note that the average minimum guaranteed secrecy capacity → 0, unlike the case where can be positive, even as σ2 e artiﬁcial noise is not used (i.e., if only the information bearing signal is transmitted). To see this, consider a speciﬁc choice for signal and artiﬁcial noise powers, σ2 u = θP0 and v = (1− θ)P0/(NT − 1), for some ﬁxed θ. Now, the second σ2 term in (9) is a constant, while the ﬁrst term tends to inﬁnity, as P0 → ∞. Thus, Ca → ∞, as P0 → ∞ which shows that Ca sec,mg is non-zero for large enough P0. Further, → ∞ (e.g., when the eavesdropper is much farther as σ2 e from the transmitter, than is the receiver), the second term in (8) goes to zero, for any choice of σ2 sec can be maximized by choosing σ2 u = P0, hence obtaining average capacity as the average minimum guaranteed secrecy capacity. → ∞, while Fig. 4 shows that Ca Ca sec achieves capacity when σ2 → 0. sec achieves a non-zero Ca sec,mg when σ2 v. Now, Ca u, σ2 sec,mg e e IV. ARTIFICIAL NOISE USING RELAYS In Section III, we saw that multiple antennas at the trans- mitter can be used to produce artiﬁcial noise. We now consider the case when the transmitter has only a single antenna. The method used in the previous section can no longer be used here. However, we assume that several relays are present to aid the secret transmission of information. Coordination with the relays can, hopefully, simulate the effect of multiple antennas in producing artiﬁcial noise. However, as opposed to the case of multiple transmit antennas, the relays are not in direct control of the transmitter. How can they then coordinate in transmitting the artiﬁcial noise (which, by deﬁnition, is random and cannot be known to the relays)? We now describe a novel 2-stage protocol that achieves this coordination. In the ﬁrst stage, the transmitter and the receiver both transmit independent artiﬁcial noise signals to the relays. The relays and the eavesdropper receive different linear combinations of these two signals. In the second stage, the relays simply replay a weighted version of the received signal, using a publicly available sequence of weights (i.e., weights that may also be known to the eavesdropper). At the same time, in this second stage, the transmitter transmits its secret message, along with a weighted version of its artiﬁcial noise, which was transmitted in the ﬁrst stage. The weighted version is generated such i that the artiﬁcial noise component due to the transmitter is canceled at the receiver. The artiﬁcial noise component due to the receiver is known to the receiver, and can be canceled off by the receiver. The two stages are now described in detail. In this section, the subscript for time, k will be suppressed for ease of presentation. Note that the information theoretic results used in this section hold, when a sequence of received samples is considered. Stage 1: A and B transmit αAB x and y respectively. Hi and E receive, respectively, rHi = αAHi αAB x + αBHi y + ni rE,1 = αAE αAB x + αBE y + e1 Stage 2: A and Hi transmit − and βi rHi respectively. B and E receive, i βi αAHi αHiB x + z (10) (11) rB = αAB z + rE,2 = αAE z + βi αHiB(αBHi y + ni) + n0 (12) βi αAHi[αAB αHiE − αAEαHiB] x + i βiαBHi αHiE y + βi αHiE ni + e2. (13) i i Here, {ei}2 i=1, {ni}N i=0 are AWGN noise samples of variance σ2 e and σ2 n respectively. (11) and (13) are normalized so that E[|αAE|2] = 1. This allows us to model the transmitter- eavesdropper distance through σ2 e . βi are (publicly known) i.i.d. complex Gaussian random weights used by the relays. z is the Gaussian information bearing signal which must be communicated by A to B, while x and y are transmitted to conceal the transmission of z. Note that y is known to the receiver, and hence, the receiver can easily cancel it off. Thus, the equivalent channel from A to B is given by ˜rB = αABz + nB, (14) of − NH where nB = i=1 βiαHiBni+n0. Note how A’s transmission NH i=1 βiαAHi αHiBx cancels out the transmission of the relays precisely, only at the intended receiver, but not at the eavesdropper, thus causing artiﬁcial noise in the latter. Thus, the coordination with the relays enabled the transmitter to generate artiﬁcial noise, such that it degrades only the eavesdropper’s channel. Varying the βi performs the same function as varying wk in Scenario 1, and thus, reduces the probability of the artiﬁcial noise being nulled at the eavesdropper. The channel from A to E can be written as, rE = hzz + Hxy hz = 0 , n = αAE αAB αAE (15) , (16) NH e1 x y + n, NH i=1 βiαBHi αHiE αBE i=1 βi αHiE ni + e2 , γ Hxy = (17) αHiE − where γ NH i=1 βiαAHi αHiB. Note that (14), (15) are similar to αAE the ones obtained for the multiple antenna scenario (4), (5). Eq. (15) represents a Single Input Multiple Output (SIMO) channel which is degraded by both AWGN and interference, NH i=1 βi αAHi αAB =

2184 IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 7, NO. 6, JUNE 2008 and its capacity is given by [16], , 0 η (18) (19) z + K| − log |K|, zσ2 x + |h12|2σ2 y + σ2 |h11|2σ2 C = log |hzh† K = i=1(|αHiE|2σ2 0 e NH x+|h22|2σ2 y+ where h11, h12, h21, h22 are the elements of Hxy, and η = |h21|2σ2 e. Note that the off-diagonal elements of K are zero, because βi’s are assumed complex Gaussian. Thus, the lower bound on secrecy capacity is given by, sec = I(Z; ˜RB) − I(Z; RE,1, RE,2) Ch n+σ2 βi)σ2 = log(1 + |αAB|2σ2 z/σ2 i=1(|αHiB|2σ2 where σ2 in expressions in (7) and (20). nB = NH nB )−log|hzh† n + σ2 βi)σ2 (20) z + K|/|K|,(21) zσ2 e . Note the similarity Ch is given by f2(σ2 x + (NH ξ + 1)σ2 sec is a random variable because it is a function of random channel gains. The (average) total power, transmitted by all y, σ2 x, σ2 z, ξ) = nodes, in the two stages, (2NHξ + 1)σ2 z + NH ξσ2 n, where we βi = ξ ∀i for simplicity. Further, it is assumed that choose σ2 E[|αXY |2] = 1. The combination of powers (σ2 x, σ2 z, ξ) is chosen to maximize the average Ch sec and hence, E[log(1 + |αAB|2σ2 y + σ2 y, σ2 Ch .= z/σ2 nB ) sec x,σ2 f2(σ2 max y,σ2 − log |hzh† z,ξ)≤P0 z + K|/|K|], zσ2 (22) where the expectation is over all the channel gains. Note that the total transmit power (including transmit power of relays) is constrained to P0. sec,mg can be obtained by putting σ2 Again, secrecy capacity depends on the AWGN power seen by the eavesdropper σ2 e. The average minimum guaranteed e = 0. secrecy capacity, Ch It is clear that by choosing the speciﬁc values, σ2 z = θ0P0, σ2 x = θ1P0, σ2 y = θ2P0 (where θ0, θ1, θ2 > 0 and satisfy the e = 0, and letting P0 → ∞, the power constraint), putting σ2 second term in (22) is a constant, while the ﬁrst term goes → ∞, as P0 → ∞. Further, to inﬁnity. Therefore, Ch → ∞, the second term in (22) goes to zero. In that as σ2 e case, the ﬁrst term can be maximized by choosing σ2 βi = 0 and setting σ2 z = P0, thus achieving average capacity of the transmitter-receiver link as the average minimum guaranteed secrecy capacity. Fig. 5 shows that Ch sec achieves the usual Shannon capacity when σ2 sec achieves a non- → 0. e zero Ch → ∞, while Ch sec,mg when σ2 sec,mg e V. ARTIFICIAL NOISE IN MIMO SCENARIO In the previous two sections, we presented methods for artiﬁcial noise generation, both using multiple transmit an- tennas and relays, assuming a single-antenna eavesdropper. It was shown that in both the scenarios, some minimum secrecy capacity can be guaranteed, using artiﬁcial noise, so long as the transmitter, along with relays, has more than one antenna. We now consider an extension of the multiple antenna scenario where all the nodes, including the eavesdropper, can have multiple antennas. In recent years, several results have char- acterized the capacity of such Multiple Input Multiple Output (MIMO) communication systems, showing a linear increase in capacity with the minimum of the number of transmit and receive antennas [7]. In this section, we characterize the minimum guaranteed ‘MIMO secrecy capacity’, and show that it does not necessarily grow linearly with the minimum of the number of transmit and receive antennas, and thus behaves differently from the usual MIMO capacity. Consider the case where NR = NE, i.e., both the receiver and the eavesdropper have similar capabilities. An increase in the number of receive antennas affects two aspects of secrecy capacity; the ability to utilize ‘parallel channels’ and the ability to produce artiﬁcial noise. Intuitively, the more the number of receive antennas, more the number of parallel channels that can be created between the transmitter and the receiver, leading to capacity gain. On the other hand, more receive antennas (and thus, more eavesdropper antennas) requires artiﬁcial noise to be produced in more dimensions, thus limiting the number of dimensions available for in- formation transmission. These two opposing effects suggest that the effect of increasing NR(= NE) on MIMO secrecy capacity is not obvious. [6] investigated the notion of MIMO secrecy capacity and showed that its behavior differs from that of capacity. However, [6] considered the case when the eavesdropper’s channel is degraded with AWGN. We now consider the worst case scenario, where the eavesdropper’s channel has no AWGN, and hence characterize the minimum guaranteed secrecy capacity. The transmission strategy needs to be modiﬁed compared to [6], in order to obtain non-zero secrecy capacity. A. Artiﬁcial Noise Generation in MIMO Scenario Equations (1), (2) hold in this case, except that we have matrix channels Hk and Gk. The elements of noise vectors, nk and ek are i.i.d. AWGN samples. The transmitter transmits xk as in (3), where Hkwk = 0, so that wk = Zkvk. However, in this case we choose Zk to be a subset of an orthonormal basis of the null space of Hk. The receiver and the eaves- dropper receive vector signals zk and yk, respectively. Based on (5), the eavesdropper E observes colored Gaussian noise with covariance K = (GkZkZ† e. Now, the lower bound on secrecy capacity is given by [2], [15], v + Iσ2 G† k k)σ2 |−log |K + GkQsG† k |/|K| (23) ,(24) sec = I(Z; S) − I(Y; S) Ca =log|Iσ2 n + HkQsH† k k G† in (23), where K = (GkZkZ† where Qs = E[sks† k] and sk is complex Gaussian distributed. The minimum guaranteed secrecy capacity can be obtained by substituting K with K k)σ2 v. We immediately note that in order to avoid the case |K| = 0, the rank of Zk (which lies in the null-space of Hk), must be at least NE. Thus, the transmitter must use at least NE dimensions for artiﬁcial noise. The remaining dimensions can be used for transmitting the information signal. Let NN D and NS denote the number of dimensions used for artiﬁcial noise and the information signal, respectively. The transmitter ﬁrst chooses NN D, where NE ≤ NN D ≤ NT − 1. It then determines NS = min(NR, NT − NN D). Then, it designs Qs and Zk, based on Hk. Let the Singular Value Decom- position (SVD) of Hk be given by Hk = UkΛkV† k. The transmitter chooses sk = Vkrk, where rk is the information

GOEL and NEGI: GUARANTEEING SECRECY USING ARTIFICIAL NOISE 2185 r,i r,1, . . . , σ2 r,NT ), with {σ2 signal. The receiver processes the received signal (zk) by multiplying it by U† k. Then, the equivalent channel to the receiver becomes ˜zk = Λkrk + ˜nk, where the components of ˜nk are i.i.d. complex Gaussian with mean 0 and variance σ2 n. To maximize the mutual information between the transmitter and the receiver, the transmitter chooses Qr = E[rkr† k] = } chosen according to the diag(σ2 waterﬁlling solution, corresponding to the NS largest singular values of Hk, with power constraint of Pinf o(≤ P0). Zk consists of NN D columns of Vk, which do not contribute to the signal space. Then, the minimum guaranteed secrecy capacity is given by, sec,mg = log |Iσ2 n + ΛkQrΛ† Ca where K = K + GkVkQrV† sec,mg is a random variable because it is a function of random channel gains Hk and Gk. We assume that the total transmit power, given by trace(E[xkx† v, is constrained to P0. Now, Pinf o = trace(VkQrV† v are chosen to maximize the average Ca sec,mg, k]) = trace(VkQrV† |K|/|K| | − log G† k), NN D and σ2 k) + NN D σ2 k. Ca (25) k k , where P is a permutation matrix, and (a) holds because the elements of ˜G1 are circularly symmetric i.i.d. complex Gaussian random variables. Let N be the number of such permutation matrices. Then, S(Σs) = 1 N E[log | ˜G1PΣsP† ˜G† 1 + ˜G2 ˜G† |] 2σ2 v P |] 2σ2 v b≤ E[log | ˜G1 1 ) ˜G† 1 + ˜G2 ˜G† (PΣsP† N P = E[log | ˜G1 ˜G† |] p + ˜G2 ˜G† 1σ2 2σ2 v c≤ E [ ˜G1 ˜G† p + ˜G2 ˜G† 1]σ2 2σ2 v ˜G2 = E[ ], [log | E ˜G1 log Pinf o + λiσ2 |] v (30) i where σ2 p is the arithmetic mean of the diagonal elements of Σs. (b) and (c) hold due to the concavity of log-determinant function. The expectation in the ﬁnal equation is over {λi}, which are the eigenvalues of the Wishart matrix ˜G2 ˜G† 2, which have the following distribution [17], [18]. ⎧⎨ ⎩ 1 π 0, 2 1 + β−1 λ − 1 4 β λ √ √ β−1)2≤ λ≤( , if ( otherwise, β+1)2 Ca sec,mg .= tr(VkQrV† max k)+NN Dσ2 v≤P0 E[Ca sec,mg], (26) p(λ)= where the expectation is over the random gains Hk, Gk. B. Asymptotic Results V† Σs 0 0 0 V† Analytical results on (usual) MIMO capacity are available for the asymptotic case of large number of antennas. We derive similar analytical results for MIMO secrecy capacity Ca sec,mg, for large number of antennas. (We also compare the two through numerical results, later in this section.) The presence of artiﬁcial noise signiﬁcantly complicates the asymptotic k. The analysis. Recall transmitter chooses NN D, and then designs the covariance matrices for artiﬁcial noise (Qn), and (Qs), the SVD of Hk = UkΛkV† that 0 0 0 INN D σ2 v k, Qs = Vk Qn = Vk k, (27) where Σs is a NS × NS diagonal matrix, obtained as the waterﬁlling solution over the NS largest singular values of Hk. Let V1 denote the matrix with the ﬁrst NS columns of Vk, and V2 denote the matrix with last NN D columns of Vk. Then, Qs = V1ΣsV† 1, and Zk = V2. We deﬁne .= G V2, which represent the equivalent ˜G1 channels from the information signal rk and artiﬁcial noise signal vk respectively, to the eavesdropper. Note that due to the orthonormality of [V1, V2], ˜G1 and ˜G2 both have circularly symmetric i.i.d. complex Gaussian distributed elements. Eq. (26) can now be written as, .= G V1 and ˜G2 sec,mg = tr(VkQrV† − log| ˜G1Σs ˜G† | |]. (28) Now, the second term can be written as a function of Σs as, S(Σs) = E[log | ˜G1Σs ˜G† E[log |Iσ2 v≤P0 | + log | ˜G2 ˜G† 2σ2 v max k)+NN Dσ2 1 + ˜G2 ˜G† n + ΛkQrΛ† 1 + ˜G2 ˜G† |]. Then, 2σ2 v Ca k 2σ2 v S(PΣsP† ) = E[log | ˜G1PΣsP† ˜G† 1 + ˜G2 ˜G† |] 2σ2 v a= S(Σs), (29) (31) where β = max(NE/(NT − NR), (NT − NR)/NE). The use of permutation matrix P and expectation over ˜G1 resulted in an upper bound on S(Σs) in terms of only the eigenvalues of ˜G2 ˜G† Ca 2. Therefore, ≥ Ca sec,mg sec,mg(LB) = tr(VkQrV† max k)+NN Dσ2 Pinf o + λiσ2 v v≤P0 E[log |Iσ2 n + ΛkQrΛ† k | − ]. (32) log i λiσ2 v Now, given the distribution of eigenvalues of a Wishart matrix (31), the lower bound obtained in (32), can be computed numerically. Note that for the ﬁrst term in (32), we consider the NS largest eigenvalues, and hence, the distribution given in (31) has to be modiﬁed appropriately, as follows. In the limit of large number of antennas, the distribution of eigenvalues can be used as a histogram. Let λth be such that, p(λ)dλ = NS/NR. Then, the distribution of one of the ∞ λth largest NS eigenvalues is given by, pNS(λ) = p(λ) · NR/NS, λ > λth 0, otherwise. 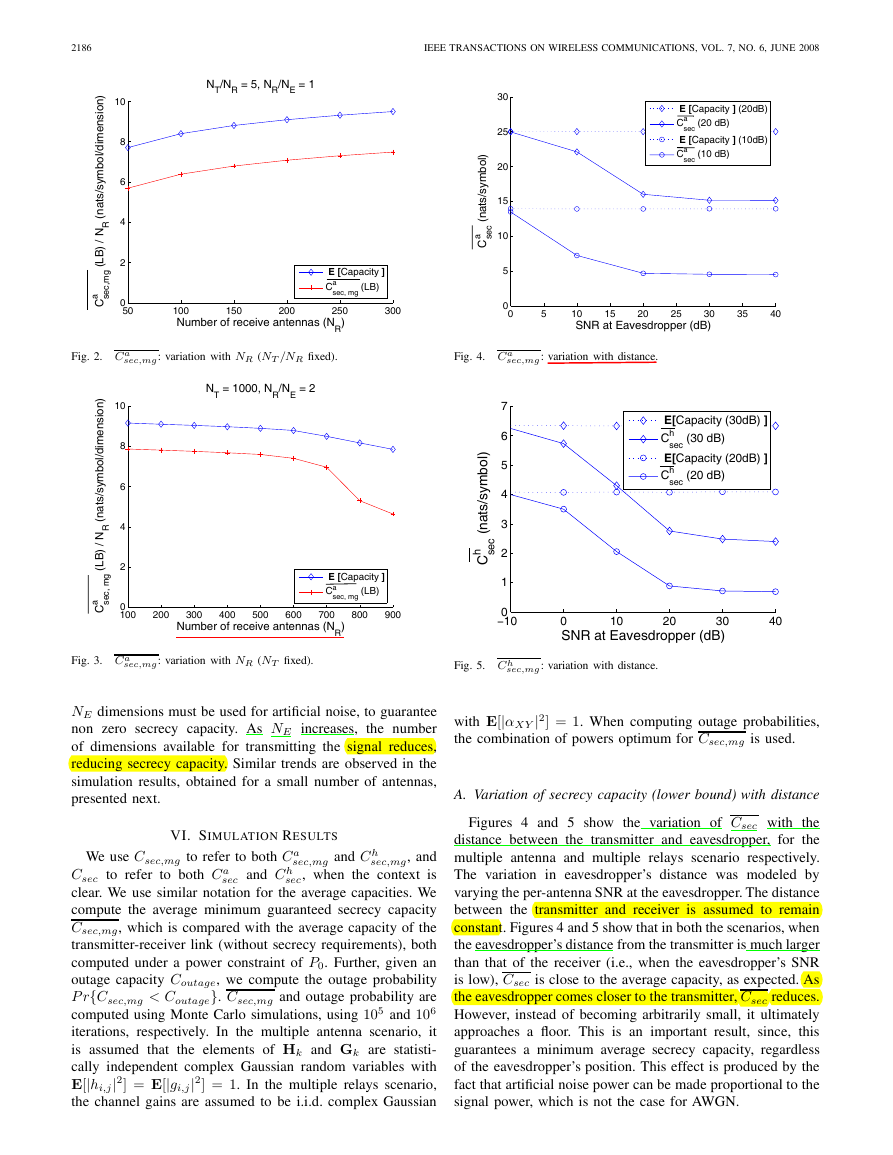(33) sec,mg(LB) (normalized Fig. 2 shows the variation of Ca w.r.t. NR) calculated using (32), as a function of NR, with NT /NR = 5 and NR/NE = 1. Note that the variation of sec,mg(LB) with NR is similar to that of average capacity, in Ca this case. Intuitively, a ﬁxed proportion of the dimensions are used to produce artiﬁcial noise, and the number of dimensions used to transmit the signal also increases proportionally. Thus, sec,mg(LB) increases with the number of receive antennas. Ca sec,mg(LB) with NR, Fig. 3 shows the variation of Ca with NT = 1000 and NR/NE = 2. In this case, the (normalized) average capacity remains fairly constant, whereas sec,mg(LB) reduces with increasing NR, the (normalized) Ca especially when NR (= 2NE) is large. Recall that at least

2186 IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 7, NO. 6, JUNE 2008 i ) n o s n e m d i / l o b m y s / s t a n ( N / ) B L ( R g m , c e s a C 10 8 6 4 2 0 50 NT/NR = 5, NR/NE = 1 ) l o b m y s / s t a n ( c e s a C E [Capacity ] a (LB) C sec, mg 100 250 Number of receive antennas (NR) 150 200 300 30 25 20 15 10 5 0 0 5 a (20 dB) sec E [Capacity ] (20dB) C E [Capacity ] (10dB) C a (10 dB) sec 15 10 30 SNR at Eavesdropper (dB) 20 25 35 40 Fig. 2. Ca sec,mg: variation with NR (NT /NR ﬁxed). Fig. 4. Ca sec,mg : variation with distance. i ) n o s n e m d i / l o b m y s / s t a n ( R N / ) B L ( g m , c e s a C 10 8 6 4 2 0 100 200 NT = 1000, NR/NE = 2 ) l o b m y s / s t a n ( c e s h C E [Capacity ] a C (LB) sec, mg h (30 dB) sec E[Capacity (30dB) ] C E[Capacity (20dB) ] C h (20 dB) sec 7 6 5 4 3 2 1 300 400 500 600 700 Number of receive antennas (NR) 800 900 0 −10 0 30 SNR at Eavesdropper (dB) 10 20 40 Fig. 3. Ca sec,mg: variation with NR (NT ﬁxed). Fig. 5. Ch sec,mg : variation with distance. NE dimensions must be used for artiﬁcial noise, to guarantee non zero secrecy capacity. As NE increases, the number of dimensions available for transmitting the signal reduces, reducing secrecy capacity. Similar trends are observed in the simulation results, obtained for a small number of antennas, presented next. VI. SIMULATION RESULTS We use Csec,mg to refer to both Ca sec and Ch sec,mg and Ch sec,mg, and Csec to refer to both Ca sec, when the context is clear. We use similar notation for the average capacities. We compute the average minimum guaranteed secrecy capacity Csec,mg, which is compared with the average capacity of the transmitter-receiver link (without secrecy requirements), both computed under a power constraint of P0. Further, given an outage capacity Coutage, we compute the outage probability P r{Csec,mg < Coutage}. Csec,mg and outage probability are computed using Monte Carlo simulations, using 105 and 106 iterations, respectively. In the multiple antenna scenario, it is assumed that the elements of Hk and Gk are statisti- cally independent complex Gaussian random variables with E[|hi,j|2] = E[|gi,j|2] = 1. In the multiple relays scenario, the channel gains are assumed to be i.i.d. complex Gaussian with E[|αXY |2] = 1. When computing outage probabilities, the combination of powers optimum for Csec,mg is used. A. Variation of secrecy capacity (lower bound) with distance Figures 4 and 5 show the variation of Csec with the distance between the transmitter and eavesdropper, for the multiple antenna and multiple relays scenario respectively. The variation in eavesdropper’s distance was modeled by varying the per-antenna SNR at the eavesdropper. The distance between the transmitter and receiver is assumed to remain constant. Figures 4 and 5 show that in both the scenarios, when the eavesdropper’s distance from the transmitter is much larger than that of the receiver (i.e., when the eavesdropper’s SNR is low), Csec is close to the average capacity, as expected. As the eavesdropper comes closer to the transmitter, Csec reduces. However, instead of becoming arbitrarily small, it ultimately approaches a ﬂoor. This is an important result, since, this guarantees a minimum average secrecy capacity, regardless of the eavesdropper’s position. This effect is produced by the fact that artiﬁcial noise power can be made proportional to the signal power, which is not the case for AWGN.

GOEL and NEGI: GUARANTEEING SECRECY USING ARTIFICIAL NOISE 2187 ) l o b m y s / s t a n ( g m , c e s a C 30 25 20 15 10 5 0 5 NR = 4, NE = 8 E [Capacity ] (N = 20) T E [Capacity ] (N = 10) T (N = 20) T (N = 10) T a C sec, mg a C sec, mg 10 15 SNR P0/σn 2 (dB) ) l o b m y s / s t a n ( g m , c e s a C 25 20 15 10 5 0 1 2 20 NT = 10 E [Capacity ] a C sec, mg a C sec, mg a C sec, mg (N = 2) E (N = 5) E (N = 8) E 4 3 8 Number of receive antennas (NR) 5 6 7 Fig. 6. Ca sec,mg: variation with P0. Fig. 8. Ca sec,mg : variation with NE and NR. E [Capacity ] (N = 4, 10) H ] (N = 4) H ] (N = 10) H h E [C sec, mg h E [C sec, mg 8 7 6 5 4 3 2 1 ) l o b m y s / s t a n ( ] g m , c e s h C [ E 0 20 22 24 SNR P0/σe 26 2 (dB) 2 ) l o b m y s / s t a n ( g m , c e s a C 25 20 15 10 5 0 1 2 28 30 E [Capacity ] a (N /N C R sec, mg a (N C /N R sec, mg = 2) E = 1) E 3 4 5 Number of Receive Antennas (NR) 6 7 8 9 10 9 10 Fig. 7. Ch sec,mg: variation with P0. Fig. 9. Ca sec,mg : ﬁxed ratio of NE and NR. 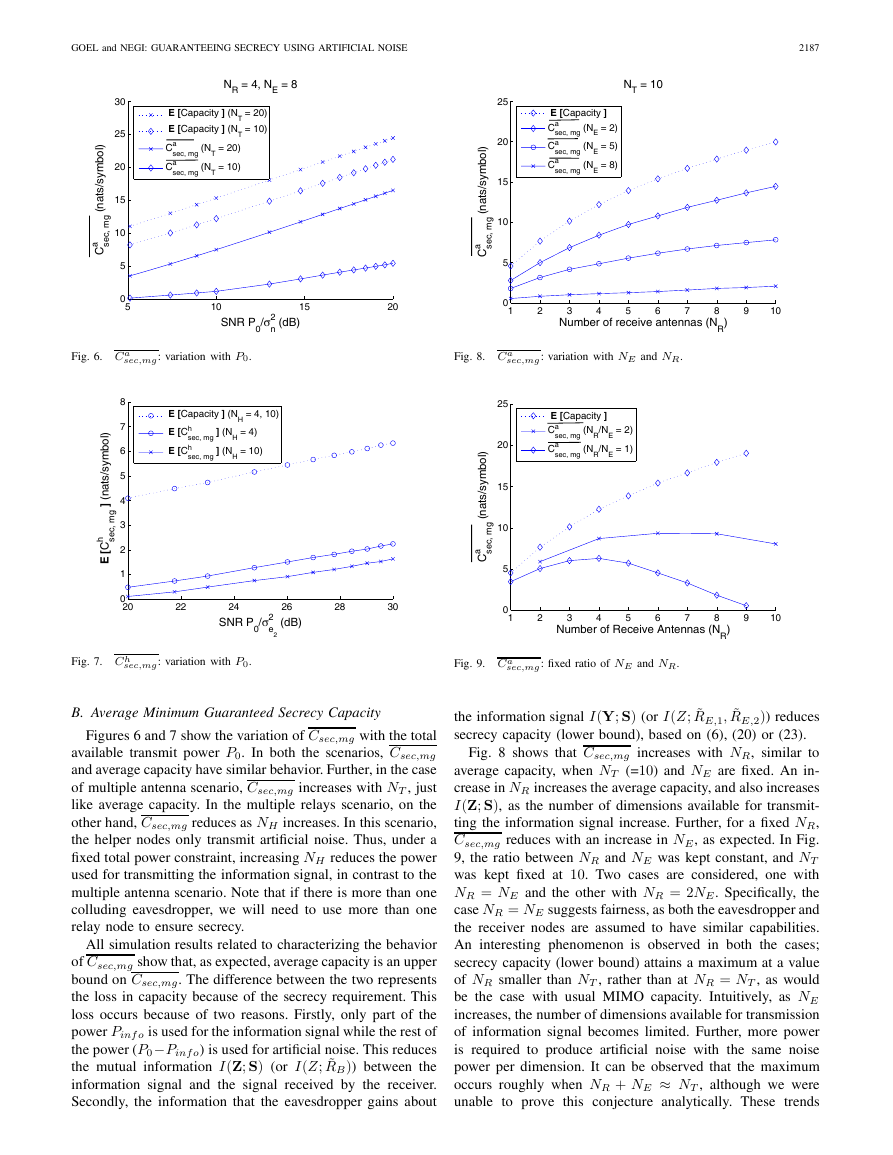B. Average Minimum Guaranteed Secrecy Capacity Figures 6 and 7 show the variation of Csec,mg with the total available transmit power P0. In both the scenarios, Csec,mg and average capacity have similar behavior. Further, in the case of multiple antenna scenario, Csec,mg increases with NT , just like average capacity. In the multiple relays scenario, on the other hand, Csec,mg reduces as NH increases. In this scenario, the helper nodes only transmit artiﬁcial noise. Thus, under a ﬁxed total power constraint, increasing NH reduces the power used for transmitting the information signal, in contrast to the multiple antenna scenario. Note that if there is more than one colluding eavesdropper, we will need to use more than one relay node to ensure secrecy. All simulation results related to characterizing the behavior of Csec,mg show that, as expected, average capacity is an upper bound on Csec,mg. The difference between the two represents the loss in capacity because of the secrecy requirement. This loss occurs because of two reasons. Firstly, only part of the power Pinf o is used for the information signal while the rest of the power (P0−Pinf o) is used for artiﬁcial noise. This reduces the mutual information I(Z; S) (or I(Z; ˜RB)) between the information signal and the signal received by the receiver. Secondly, the information that the eavesdropper gains about the information signal I(Y; S) (or I(Z; ˜RE,1, ˜RE,2)) reduces secrecy capacity (lower bound), based on (6), (20) or (23). Fig. 8 shows that Csec,mg increases with NR, similar to average capacity, when NT (=10) and NE are ﬁxed. An in- crease in NR increases the average capacity, and also increases I(Z; S), as the number of dimensions available for transmit- ting the information signal increase. Further, for a ﬁxed NR, Csec,mg reduces with an increase in NE, as expected. In Fig. 9, the ratio between NR and NE was kept constant, and NT was kept ﬁxed at 10. Two cases are considered, one with NR = NE and the other with NR = 2NE. Speciﬁcally, the case NR = NE suggests fairness, as both the eavesdropper and the receiver nodes are assumed to have similar capabilities. An interesting phenomenon is observed in both the cases; secrecy capacity (lower bound) attains a maximum at a value of NR smaller than NT , rather than at NR = NT , as would be the case with usual MIMO capacity. Intuitively, as NE increases, the number of dimensions available for transmission of information signal becomes limited. Further, more power is required to produce artiﬁcial noise with the same noise power per dimension. It can be observed that the maximum occurs roughly when NR + NE ≈ NT , although we were unable to prove this conjecture analytically. These trends

分享到：

赞收藏

资料库

guaranteeing secrecy using artificial noise.pdf

相关推荐

课程资源

热门标签

最新资料