第1页 / 共17页
第2页 / 共17页
第3页 / 共17页
第4页 / 共17页
第5页 / 共17页
第6页 / 共17页
第7页 / 共17页
第8页 / 共17页
本人建模大作业.docx
数学建模作业
1、用穷举法与Q值递归法解决名额分配问题结果是否
相同，若相同，证明之，若不同给出反例，再不行就
给出100组例子。
穷举法matlab程序
a=randint(100,2,[50,100]);
n=randint(100,1,[20,40]);
q=[];n1=[];n2=[];
for(i=1:100)
t=[];
for(j=1:(n(i,1)-1))
p=n(i,1)-j;
if(a(i,1)/j>=a(i,2)/p)
tj=(a(i,1)/j-a(i,2)/p)/(a(i,2)/p);
else
tj=(a(i,2)/p-a(i,1)/j)/(a(i,1)/j);
end
t(1,j)=tj;
end
a(i,1);
a(i,2);
n(i,1);
[q(i),n1(i,1)]=min(t);
n2(i,1)=n(i,1)-n1(i,1);
end
Q值法matlab程序
n1=randint(100,1,[2,8]);n2=randint(100,1,[2,8]);
for(i=1:100)
while n1(i,1)+n2(i,1)=Q2)
%
n1(i,1)=n1(i,1)+1;
else
n2(i,1)=n2(i,1)+1;
end
end
n1(i,1);
n2(i,1);
end
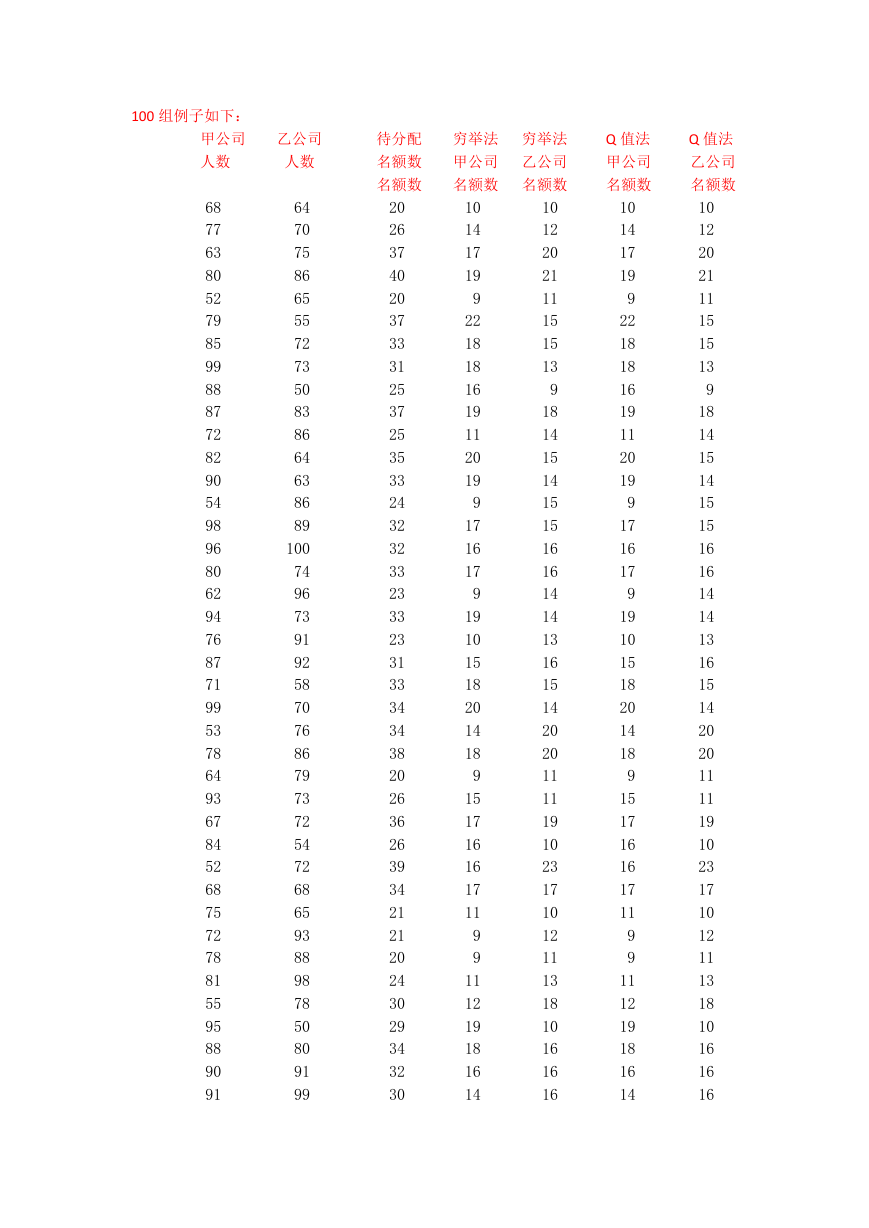
100 组例子如下：
甲公司
人数
乙公司
人数
待分配
名额数
名额数
穷举法 穷举法
甲公司 乙公司
名额数 名额数
Q 值法
甲公司
名额数
Q 值法
乙公司
名额数
68
77
63
80
52
79
85
99
88
87
72
82
90
54
98
96
80
62
94
76
87
71
99
53
78
64
93
67
84
52
68
75
72
78
81
55
95
88
90
91
64
70
75
86
65
55
72
73
50
83
86
64
63
86
89
100
74
96
73
91
92
58
70
76
86
79
73
72
54
72
68
65
93
88
98
78
50
80
91
99
20
26
37
40
20
37
33
31
25
37
25
35
33
24
32
32
33
23
33
23
31
33
34
34
38
20
26
36
26
39
34
21
21
20
24
30
29
34
32
30
10
14
17
19
9
22
18
18
16
19
11
20
19
9
17
16
17
9
19
10
15
18
20
14
18
9
15
17
16
16
17
11
9
9
11
12
19
18
16
14
10
12
20
21
11
15
15
13
9
18
14
15
14
15
15
16
16
14
14
13
16
15
14
20
20
11
11
19
10
23
17
10
12
11
13
18
10
16
16
16
10
14
17
19
9
22
18
18
16
19
11
20
19
9
17
16
17
9
19
10
15
18
20
14
18
9
15
17
16
16
17
11
9
9
11
12
19
18
16
14
10
12
20
21
11
15
15
13
9
18
14
15
14
15
15
16
16
14
14
13
16
15
14
20
20
11
11
19
10
23
17
10
12
11
13
18
10
16
16
16
84
60
63
81
77
53
54
63
70
74
96
80
66
74
80
58
92
98
80
51
91
81
85
54
71
69
58
92
92
73
98
57
94
89
72
81
98
82
62
67
59
75
70
73
61
85
76
97
86
61
72
58
99
68
52
88
95
64
62
97
56
97
85
93
60
73
54
93
78
66
69
94
68
53
60
52
78
56
76
55
89
69
91
52
80
98
64
95
21
24
27
25
36
26
33
40
30
39
37
39
22
37
39
23
22
36
35
33
35
33
38
25
28
24
20
21
37
27
29
39
24
38
33
38
30
40
27
31
23
30
28
33
12
10
12
11
17
12
14
21
12
20
24
19
9
20
22
9
14
18
17
12
21
17
23
9
13
12
9
10
21
16
18
20
13
23
16
23
16
22
11
17
10
13
15
14
9
14
15
14
19
14
19
19
18
19
13
20
13
17
17
14
8
18
18
21
14
16
15
16
15
12
11
11
16
11
11
19
11
15
17
15
14
18
16
14
13
17
13
19
12
10
12
11
17
12
14
21
12
20
24
19
9
20
22
9
14
18
17
12
21
17
23
9
13
12
9
10
21
16
18
20
13
23
16
23
16
22
11
17
10
13
15
14
9
14
15
14
19
14
19
19
18
19
13
20
13
17
17
14
8
18
18
21
14
16
15
16
15
12
11
11
16
11
11
19
11
15
17
15
14
18
16
14
13
17
13
19
81
53
66
81
58
81
62
79
75
73
77
98
67
70
65
70
55
53
61
97
53
63
100
60
75
64
84
98
89
83
56
54
34
40
24
22
31
40
20
38
20
30
24
35
25
39
22
30
20
20
12
10
16
22
8
22
10
16
11
17
11
18
12
17
14
20
12
12
15
18
12
16
10
14
13
18
14
21
10
13
20
20
12
10
16
22
8
22
10
16
11
18
11
18
12
17
14
20
12
12
15
18
12
16
10
14
13
17
14
21
10
13
通过程序的运行，我们可以清晰的看到用 Q 值法和穷举法解决名额分配问题结果是相同的。
2、以阅历构建微分方程模型。
人口系统数学模型的建立
用来描述人口系统中人的出生、死亡和迁移随时间变化的情况，以及它们之间定
量关系的数学方程式或方程组，又称人口模型。人口控制论和人口系统工程的首
要任务是建立人口系统的数学模型。根据人口系统的反馈机制，明确区分状态变
量、控制变量和观测量，可以建立人口系统的闭环控制模型。模型是对实体的近
似描述，如果模型精度满足所研究问题的要求，模型便被认为是准确的。用中国
人口统计数据校验有关人口系统数学模型时，其近期精度达到 0.1％左右,这表明
中国人口模型的精度很高。
发展概况 20 世纪 30 年代 A.J.洛特卡建立了人口的定常积分方程模型。40
年代莱斯利建立了差分方程组模型。60 年代又出现了弗尔斯特的偏微分方程模
型。70 年代波拉德在莱斯利模型基础上提出了随机模型。建立完善的人口系统
闭环控制模型，则是最近几年的事。中国控制论学者在这项工作中取得了重要成
果。
分类 人口模型分为两类，一类是确定性模型，另一类是随机模型。如果按
年龄和时间是连续量还是离散量，又可将人口模型分为连续模型和离散模型两种。
连续模型是由偏微分方程描述的带边界控制的分布参数系统，离散模型是由差分
方程组描述的双线性系统。离散模型可用离散化方法从连续模型得到。连续模型
便于理论分析，而离散模型适合于计算机仿真。
人口系统连续模型 两个自变量的函数 N(
人口总数，称为人口函数。P( , ＝ N( , )/
连续模型为
, )代表 时刻一切年龄小于 的
,称为人口密度函数 则人口系统
[368-01]
(1)式中 ( ， )是相对死
亡率函数， ( , )为人口迁移率函数， ( )为绝对出生率函数,U( )为相对出生率
函数，P0( )为初始年龄密度函数。在(1)中唯一能控制的是出生率 ( ),它是系
统的控制变量。它出现在系统的边界条件中，所以模型 (1)又称为边界控制的分
布参数系统。这里的 ( )并不与实时人口状态 P( , )发生联系，所以这种控制
又称为开环控制。
实际上， ( )应与 时刻的人口状态，特别是与处在生育期内妇女的生育水
平有密切关系。考虑到这一特点又有如下的人口闭环控制模型：
[368-02]
)称作妇女总
和生育率,它是人口系统的控制变量。中国人口控制和计划生育是靠控制 β( )来
进行的。[ 1， 2]称为妇女育龄区间, 1 为最小生育年龄， 2 为最高生育年龄，
K( ， )为女性比例函数， ( , )为妇女生育模式，满足归一化条件：
(2)式中β(
[368-03]
在模型(2)中, ( )与 时刻的人口状态 P( , )建
立了直接关系，这在控制论中称为实时状态反馈，这种控制形式称为闭环控制（见
闭环控制系统）。
人口系统离散模型 如果用 0( ), 1( ), 2( ),…,
( )表示 时刻的年龄构
成,其中 ( )表示 年代年满 周岁但不到 ＋1 周岁的人口数，写成向量形式
[368-05]
则离散人口模型可写成
[368-06]
维数的矩阵，
(3)式中 H( )，B( )为相应
[368-07]
式 中
[368-08]
称 为 按 龄 死 亡 率 , 为 人 类 能 活 到 的 最 高 年
龄
;[368-090]
[368-09]
称为婴儿死亡率；K （ ）为女性比例函数； （ ）为
； (
妇女生育模式,服从归一化条件[369-01]
)为人口迁移向量； 0
为人口初始年龄状态;β( )为妇女总和生育率,它是系统控制变量; ( )是人口状态
变量。模型 (3)是一个双线性系统。在这个模型中,[369-02]
人口经死亡后留存到下一年的人口年龄构成。而[369-03]
是 年代出
生的人口留存到下一年的人口, ( )是 年代迁移人口留存到下一年的人口。在模
型(3)中，方程左端表示 ＋1 年代的人口年龄构成,而方程右端则表现了 年代人
口年龄的变化。因此在这个模型中，时间、出生、死亡和迁移四个因素以及它们
之间的定量关系得到了完全描述。
一项是 年代
在模型(1)、(2)、(3)中,观测变量就是人口指数，例如总人口数 N( )
[369-04]
人口控制就是通过改变、调节妇女总
和生育率 β( )来控制人口状态 ( )，达到改变和控制人口趋势的目的。
参考书目
宋健、于景元：《人口控制论》，科学出版社，北京，1985。
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
