基于GM-ARIMA模型的我国入境游客人次数预测研究.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.46M 资料格式：pdf 举报版权申诉

weixin_38725015-12127561-4744300845170868325.pdf-第1页.png

第1页 / 共9页

weixin_38725015-12127561-4744300845170868325.pdf-第2页.png

第2页 / 共9页

weixin_38725015-12127561-4744300845170868325.pdf-第3页.png

第3页 / 共9页

weixin_38725015-12127561-4744300845170868325.pdf-第4页.png

第4页 / 共9页

weixin_38725015-12127561-4744300845170868325.pdf-第5页.png

第5页 / 共9页

weixin_38725015-12127561-4744300845170868325.pdf-第6页.png

第6页 / 共9页

weixin_38725015-12127561-4744300845170868325.pdf-第7页.png

第7页 / 共9页

weixin_38725015-12127561-4744300845170868325.pdf-第8页.png

第8页 / 共9页

文本预览

中国科技论文在线 http://www.paper.edu.cn 基于 GM-ARIMA 模型的我国入境游客人次数预测研究宋利勇，柳向东** （暨南大学经济学院，广州 510632）摘要：改革开放以来，我国旅游产业经历了飞速的发展，也为我国经济增长作出了突出的贡献。通过游客人次的准确预测，对旅游产业规划有重要的指导意义。本文提出一种基于 ARIMA 模型和 GM(1,1)模型的组合模型，以 1985-2018 年的我国入境游客人次数据为研究对象，先构建 ARIMA 模型，然后利用 GM(1,1)模型的残差修正法对 ARIMA 模型的残差进行拟合预测，最终得到 GM-ARIMA 的预测结果。实证结果表明，组合模型预测精度更高，能够较为准确地预测我国入境游客人次数，对旅游产业的发展具有一定的参考价值和实践意义。关键词：入境游客人次预测；ARIMA 模型；GM(1,1)模型；残差修正中图分类号：F592.3 Analysis about the Number of Inbound Tourists in China Based on GM-ARIMA Model SONG Liyong, LIU Xiangdong (School of Economics, Jinan University, Guangzhou 510632) Abstract: Since the reform and opening up, China's tourism market has experienced rapid development. The tourism industry has made outstanding contributions to the growth of China's economy. Through the accurate prediction of tourists, it has important guiding significance for tourism industry planning. This paper proposes a combined model based on ARIMA model and GM(1,1) model. Taking the data of inbound tourists in China from 1985 to 2018 as the research object, the ARIMA model is constructed first, and then the GM(1,1) model is used. The difference correction method fits and predicts the residual of the ARIMA model, and finally obtains the prediction result of GM-ARIMA. The empirical results show that the combined model has higher prediction accuracy and can accurately predict the number of inbound tourists in China, which has certain reference value and practical significance for the development of tourism industry. Key words: Inbound tourists forecast; ARIMA; GM(1,1); Residual error correction 5 10 15 20 25 30 0 引言自从 20 世纪 90 年代中后期以来，中国旅游市场的规模快速扩大。根据国家文化和旅游 35 部的政府公开信息显示，2018 年全国旅游业对 GDP 的综合贡献为 9.94 万亿元，占 GDP 总量的 11.04%。旅游直接就业 2826 万人，旅游直接和间接就业 7991 万人，占全国就业总人口的 10.29%。旅游产业已经成为国民的支柱性产业之一，并且带动了我国的就业水平。游客量的预测对于旅游业的发展有重要的推动作用，为旅游产业的资源和市场开发、管理和未来规划提供科学的依据，进一步提高旅游发展的质量，促进产业更高效的发展。随着近年来 40 “一带一路”倡议的重大政策，中国国际影响力不断地提升，带来了更多发展机遇。2018 作者简介：宋利勇（1995-），男，硕士研究生，主要研究方向：应用统计通信联系人：柳向东（1973-），男，教授、博士生导师，主要研究方向：统计学及其应用. E-mail: tliuxd@jnu.edu.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 年入境旅游人数为 14120 万人次，其中外国人入境旅游人数增长 4.7%，国际旅游收入达到了 1271 亿美元。本文的研究利用时间序列分析的组合模型对入境游客人次数进行预测，为相关部门制定合理的出入境旅游政策和旅游规划提供一定的参考，通过旅游业国际化布局的发展从而增强文化输出，提升国际影响力。 45 1 研究背景及模型介绍 1.1 研究背景 50 55 ARIMA 模型是由美国统计学家博克斯和英国统计学家詹金斯于 70 年代提出的，所以又称为博克斯-詹金斯模型，简称 B-J 模型。ARIMA 模型是时间序列数据的分析过程之一，在分析时间相关的序列时具有很大的优势。孙健等基于 ARIMA 模型预测研究了中国医院诊疗人次[1]；陈沛军等利用 ARIMA 模型对中国卫生总费用进行了预测分析[2]；李娜等通过最优 ARIMA 模型对我国 GDP 增长进行了预测[3]。因为单一模型有时预测精度有限，因此，较多的学者在一定的条件下会选择多个组合的方式进行修正，提高预测精度。目前，残差修正法是国内学者们的研究热点，即通过对残差序列建模，进而修正原模型，以达到提高预测的精准度目的。光辉等采用神经网络对灰色预测模型的残差修正，使得预测具有更高的的准确性和适应性[4]；吴晓峰等建立了一种基于 BP 神经网络误差纠正的 ARIMA 组合预测模型，预测了未来一段时间北京市 CPI 的走势[5]；樊娇等使用 GM-ARIMA 模型对月度售电量进行预测[6]。因此，为了提高模型的预测精度，本文通过残差修正法改进 ARIMA 模型，即通过建立 GM(1,1)对 ARIMA 模型的残差进行拟合预测，补偿原预测值，从而提高模型对我国入境游客人次数的预测精度。 60 1.2 模型介绍 1.2.1 ARIMA 模型 ARIMA 模型是一种以随机理论为基础的时间序列预测方法，该方法适用于中短期预测，具有预测精度高、使用方法简单等特点。ARIMA(p,d,q)，p 为自回归阶数， d 为时间序列称 65 为平稳序列进行差分的阶数， q 为移动平均阶数，其一般表达式为： ARIMA 模型建模的主要步骤包括以下的三个部分：（1）序列平稳化处理：根据时间序列图和单方根检验结果判断，若原时间序列不是平稳序列，应当通过差分的方法处理，将原时间序列变为平稳时间序列，差分 70 的阶数 d 需要通过单方根检验得出最优取值。（2）模型参数估计与检验：根据自相关函数图（ACF）、偏相关函数图（PACF）的拖尾与截尾的性质，选择合适的模型；经过由低阶到高阶的尝试，选取最优的模型参数值；绘制残差序列的正态 Q-Q 图，并进行显著性检验及残差的白噪声检验，如果未通过检验，应当重新选择模型。 75 （3）模型预测：运用选择的适当的 ARIMA 模型对未来三年我国入境游客人次数进行预测并分析。 - 2 - 1111ttptptqtqxxx

中国科技论文在线 1.2.2 GM(1,1)模型的残差修正法 http://www.paper.edu.cn 本文以 ARIMA 时间序列模型残差预测值，作为 GM(1,1)预测模型的输入变量，利用 GM(1,1)模型计算出 ARIMA 模型残差预测值，再与 ARIMA 模型预测结果结合。 80 GM(1,1)模型的建模步骤如下：（1）设置原始序列：，对其进行一次累加，以弱化其随机性，增强其规律性，构造累加矩阵：其中，。（2）均值生成：为的紧邻均值生成序列， 85 。，，（3）模型的建立：由建立一阶线性方程：，这就是 GM（1，1），其解为：。 2 我国入境游客人次数基于 GM-ARIMA 模型的实证分析不同模型的适用条件不同，通过对模型的组合修正，能够在一定程度上提高预测的精准 90 度。本文选取预测方法成熟的 ARIMA 时间序列并通过残差修正法改进，即通过灰色预测理论对 ARIMA 模型的预测残差修正，建立 GM-ARIMA 组合模型对我国入境游客人次数进行预测。 2.1 数据的准备研究选取的数据为 1985-2018 年我国入境游客人次数，数据整理后如下表 1，数据来源 95 于国家统计局统计年鉴。表 1 1985-2018 年我国入境游客人次数 Tab. 1 Number of inbound tourists in China in 1985-2018 年份 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 入境游客人次数（万人） 1783.31 2281.95 2690.23 3169.48 2450.14 2746.18 3334.98 3811.49 4152.69 4368.50 4638.65 5112.75 入境游客人次数（万人） 9790.80 9166.21 10903.82 12029.23 12494.21 13187.33 13002.74 12647.59 13376.22 13542.35 13240.53 12907.78 年份 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 - 3 - (0)(0)(0)(0)((1),(2),,())Eeeen(1)(1)(1)(1)((1),(2),,())Eeeen(1)(0)1()(),1,2,,nkekekkn(1)Z(1)E(1)(1)(1)1()()(1)2zkekek2,3,,kn(1)E(1)(1)dEaEudk(1)(0)ˆ(1)(1),1,2,akuuekeeknaa

中国科技论文在线 http://www.paper.edu.cn 1997 1998 1999 2000 2001 5758.79 6347.84 7279.56 8344.39 8901.30 2014 2015 2016 2017 2018 12849.83 13382.04 13844.38 13948.24 14119.83 数据来源：国家统计局实验过程将 1985-2015 年我国入境旅游人次数作为训练数据集，2016-2018 年的数据作 100 为测试集，判断模型拟合预测效果，进而对 2019-2021 年我国入境旅游人次数做出短期预测。 2.2 模型的建立首先建立 ARIMA 模型，根据表 1 所得的 1985-2015 年我国入境旅游人次数数据，绘制出时序图和相关函数图，如下图 1 所示。通过直观判断时间序列的平稳性，进行下一步的单位根检验。 105 图 1 1985—2018 年我国入境游客人次数时间序列图 Fig. 1 Time series of the number of inbound tourists from 1985 to 2018 110 图 2 我国入境游客人次数自相关系数图 Fig. 2 Self-correlation coefficient of the number of inbound tourists in China - 4 -

中国科技论文在线 http://www.paper.edu.cn 图 3 我国入境游客人次数偏相关系数图 Fig. 3 The partial correlation coefficient of the number of inbound tourists in China 115 通过图 1 显示我国入境旅游人次数表现出明显的上升趋势，同时图 2 中样本自相关函数拖尾且缓慢下降，说明该时间序列是非平稳的，需要通过差分将旅游人次数据转化为平稳的时间序列。图 4 1985—2015 年我国入境游客人次数 1 阶差分时间序列图 120 Fig. 4 The first-order differential time series of the number of inbound tourists in China from 1985 to 2015 图 5 1985—2015 年我国入境游客人次数 2 阶差分时间序列图 125 Fig. 5 The second-order differential time series of the number of inbound tourists in China from 1985 to 2015 对非平稳的原始时间序列 y，做差分处理并生成相应的时序趋势图。根据图 4 和图 5 可观察到，在进行一次和两次差分处理后的数据增减趋势都较为平缓，判断差分后的时间序列是否平稳，还要进行 ADF 单位根检验。根据 ADF 检验结果显示 1 阶差分 P 值大于 0.05，二 - 5 -

中国科技论文在线 http://www.paper.edu.cn 阶差分为 0.01，故在 5%的显著性水平下 2 阶差分序列是平稳的，1 阶差分序列为非平稳。因此确定 ARIMA（p,d,q）模型的阶数 d=2。 130 图 6 二阶差分序列的自相关分析图 Fig. 6 Autocorrelation analysis of second-order difference sequences 135 图 7 二阶差分序列的偏相关分析图 Fig. 7 Partial correlation analysis of second-order difference sequences 通过对二阶差分后平稳的时间序列自相关函数与偏自相关函数观察，初步判定 ARIMA （p,d,q）中的阶数 p、q。由图 6、图 7 我们可以看出序列的自相关和偏自相关函数都是拖尾，因此可以确定建立 ARMA（p,q）模型。二阶序列的偏自相关函数可以确定 p 值，可观察到 140 在滞后三阶时不显著，之后都在置信区间内，所以 p 可以初步确定为 3；自相关函数可以确定 q 值，因为所有滞后阶值均在置信区间内，所以 q 值初定 0、1、2。对于 p、q 选取不同的值，从低阶到高阶选择，根据 AIC 准则选择拟合最优的模型。通过对下表 2 比较可得，所建立的 ARIMA 模型中，ARIMA（3,2,0）模型的 AIC 值最小。 145 表 2 备选 ARIMA 模型拟合统计量 Tab. 2 Alternative ARIMA model fitting statistics 统计量 Log likelihood AIC 统计量 Log likelihood AIC 统计量 ARIMA(1,2,0) ARIMA(1,2,1) ARIMA(1,2,2) -202.95 409.89 -202.89 411.79 -200.77 409.54 ARIMA(2,2,0) ARIMA(2,2,1) ARIMA(2,2,2) -201.76 409.62 -200.53 409.07 -199.49 408.99 ARIMA(3,2,0) ARIMA(3,2,1) ARIMA(3,2,2) - 6 - (0)()Xk

中国科技论文在线 http://www.paper.edu.cn Log likelihood AIC -199.47 406.94 -199.31 408.62 -199.31 410.62 绘制残差序列 Q-Q 图，如下图 8 所示，能够看到数据中的点大多落在图中的直线上，说明该数据符合正态性假设。通过 Ljung-Box 检验，得到统计量 P=0.835>0.05，无统计学意义，残差序列是白噪声，因此选择 ARIMA（3,2,0）是适合的。 150 图 8 残差序列正态 QQ 图 Fig. 8 Residual sequence normal QQ diagram 然后将以上得到 ARIMA（3,2,0）模型的残差序列，作为灰色预测 GM（1,1）模型的初始值，拟合残差预测模型。在建模之前需要对残差序列做如下的数据预处理[7]：找出 155 中最小的负值，然后令，得到数列。根据 1.2.2 节中 GM（1，1）预测模型建模步骤，构建模型：发展系数-a= 0.04326788，灰色作用量 u= 403.9832。利用残差检验模型，得到相对精度为 82.00191%，C 值=0.2891794，C 值<0.35， GM(1,1)预测精度为：好。利用该模型得到误差预测序列，还原成原始数列的预测数列，其中还原公式为：。 160 最后将 ARIMA 模型的预测值和 GM（1,1）模型的残差预测值相加，构建 GM-ARIMA 模型得到修正后的模拟值: = 。 2.3 模型的检验和预测本研究使用两项误差值来对模型进行评价：（1）误差平方和，在一定程度上反应波动程度；（2）平均相对误差，不受数据多少和数值大小的影响，更能反应模型误差的程度。 165 根据上节所建立的 ARIMA 模型和 GM-ARIMA 模型对 2016-2018 年我国入境游客人次数进行模拟，模拟结果如下表 3： - 7 - (0)1E(0)1E(0)[1,min]E0(0)(0)21[1,min]()()||EnEnE(0)2E(0)2ˆE0(0)(0)12[1,min]ˆˆ()()||EnEnE(0)ˆ()Yk(0)(0)1ˆˆ()()XkEk

中国科技论文在线 http://www.paper.edu.cn 170 Tab. 3 ARIMA model and GM-ARIMA model prediction error table 表 3 ARIMA 模型和 GM-ARIMA 模型预测误差表年份实际 ARIMA 模拟值误差平均 GM-ARIMA 误差平均平方和相对误差模拟值平方和相对误差 2016 2017 2018 13844.38 13686.89 66955.11 1.022% 13746.68 14682.9 0.373% 13948.24 13843.63 14119.83 13943.17 13927.09 14051.34 由上表中的数据可以看到：ARIMA 模型和 GM-ARIMA 模型的预测平均相对误差都低于 2%，精度较高，拟合效果好，所以可以预测 2019-2021 年我国入境游客人次数。同时， GM-ARIMA 模型的平均相对误差明显小于 ARIMA 模型。因此，本文提出的组合模型预测 175 效果要优于单个的 ARIMA 模型，灰色预测模型对残差起到了修正效果，使 ARIMA 模型的预测结果于真实值之间的误差减小了，提高了预测的精度。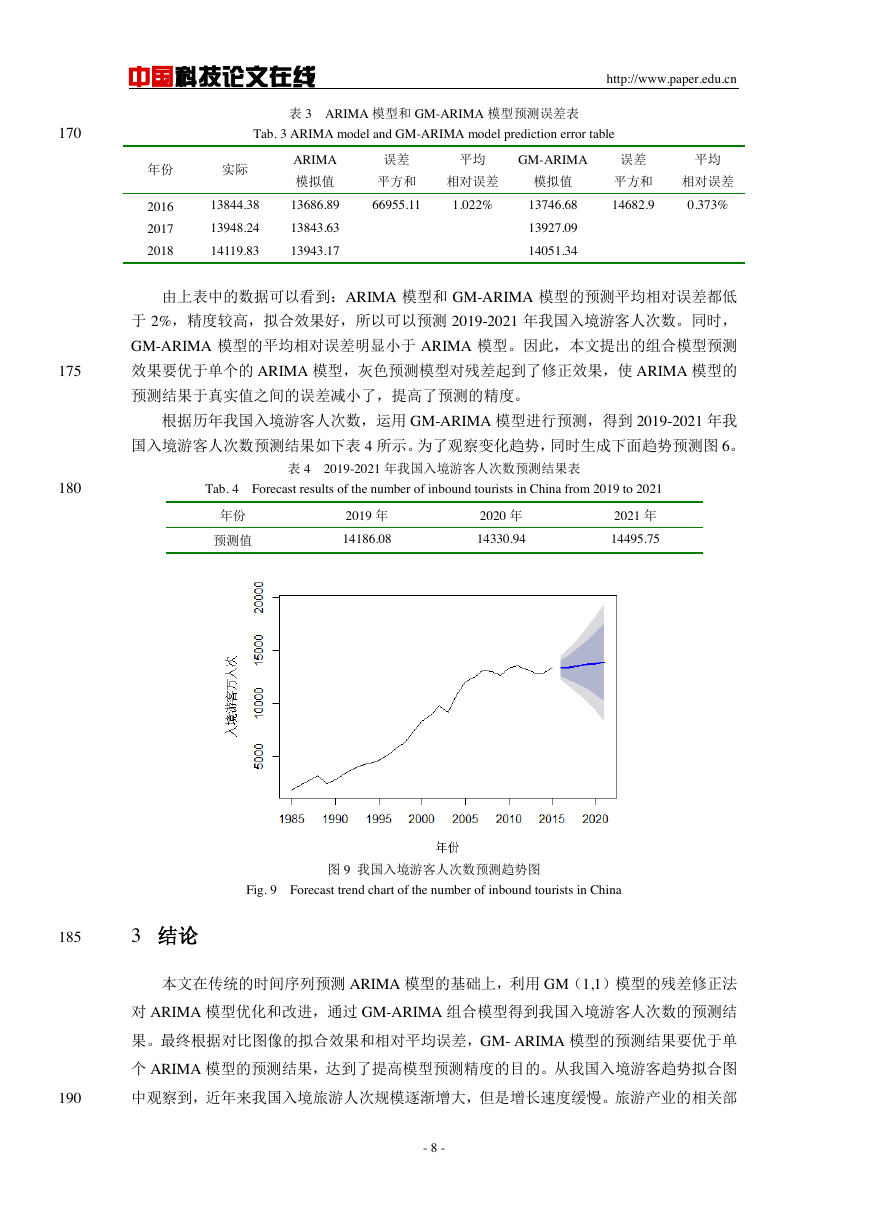根据历年我国入境游客人次数，运用 GM-ARIMA 模型进行预测，得到 2019-2021 年我国入境游客人次数预测结果如下表 4 所示。为了观察变化趋势，同时生成下面趋势预测图 6。 180 Tab. 4 Forecast results of the number of inbound tourists in China from 2019 to 2021 表 4 2019-2021 年我国入境游客人次数预测结果表年份预测值 2019 年 14186.08 2020 年 14330.94 2021 年 14495.75 图 9 我国入境游客人次数预测趋势图 Fig. 9 Forecast trend chart of the number of inbound tourists in China 185 3 结论本文在传统的时间序列预测 ARIMA 模型的基础上，利用 GM（1,1）模型的残差修正法对 ARIMA 模型优化和改进，通过 GM-ARIMA 组合模型得到我国入境游客人次数的预测结果。最终根据对比图像的拟合效果和相对平均误差，GM- ARIMA 模型的预测结果要优于单个 ARIMA 模型的预测结果，达到了提高模型预测精度的目的。从我国入境游客趋势拟合图 190 中观察到，近年来我国入境旅游人次规模逐渐增大，但是增长速度缓慢。旅游产业的相关部 - 8 -

分享到：

赞收藏

资料库

基于GM-ARIMA模型的我国入境游客人次数预测研究.pdf

相关推荐

开发技术

热门标签

最新资料