Optics Communications 391 (2017) 116–120 Contents lists available at ScienceDirect Optics Communications journal homepage: www.elsevier.com/locate/optcom Controllable autofocusing properties of conical circular Airy beams Jinggui Zhanga,⁎ , Yongfan Lia, Zuwei Tiana, Dajun Leib MARK a Department of information science and Engineering, Hunan First Normal University, Changsha 410205, China b School of Electronic Information and Electrical Engineering, Xiangnan University, Chenzhou, Hunan 423000, China A R T I C L E I N F O A B S T R A C T Keywords: Circular Airy beam Optical propagation Hankel transform In this paper, we propose a new family of circular Airy beam (CAB) through introducing a cone angle. We investigate the autofocusing properties of such conical circular Airy beam (CCAB) both analytically and numerically, particularly focusing on the novel behaviors different from the case of the conventional CAB. Under the action of positive cone angles, the autofocusing effect of CCAB is greatly strengthened, and the focal length is remarkably reduced, as compared to the case of conventional CAB. On the other hand, the autofocusing effect may be weakened or even completely eliminated, and the focal length is largely extended under the action of negative cone angles. Therefore, such dramatic enhancement or suppression of abruptly focus can be effectively controlled through adjusting the cone angle. The novel autofocusing properties will make CCAB more powerful in various applied fields including optical trapping and particle manipulation. 1. Introduction Circular Airy beams, i.e. abruptly autofocusing beams, recently have received a considerable boost in the scientific community because of its unique abruptly autofocusing behavior unattainable with conventional Gaussian beams [1,2]. Such novel beams were theoretically introduced by Efremidis et al. in 2010 [1], afterwards were experimentally observed by Papazoglou et al. [2]. The most impressive property of such CAB may well be the ability to abruptly focuses its energy right before the focal point even in the linear media while its profile keeps almost constant along the whole propagation trajectory until the focus is reached. For this reason, such abruptly autofocusing properties of CAB highlight great potential applications in biomedical treatment and optical micromanipulation etc. In optical trapping, CAB is able to yield a greater gradient force on the particles in the focal region, when compared to conventional Gaussian beams under the same initial condition [3,4]. Therefore, the CAB has been applied to trap and guide the microparticles along the desired path. In addition, engineering CAB in the Fourier space can offer a new approach to produce an elegant paraboloid optical bottle [5,6]. Recently, CAB in the form of accelerat- ing beams are demonstrated to be able to reshape into non-linear intense light bullets under the action of both multiphoton absorption and ionization in Kerr media [7]. Up to now, the control of the abruptly autofocusing property of the CAB has become a new and exciting field of research. For instance, several strategies have been proposed to enhance focal intensity, or control the focal pattern and trajectory of self-acceleration, such as adding different optical vortices [8,9], imposing the chirped phase factor [10], and blocking front light rings [11] and so on. Meanwhile, several other CABs with special properties have also been disclosed [12–14]. To control the propagation of CAB, some external physical mechanisms such as linear potential [15] and optical lattices [16] have been introduced by some researchers. Recently, initial angle as another new physical strategies is found to be able to drive the Airy beam perform ballistic dynamics, similar to those of projectiles moving under the action of gravity [17]. Meanwhile, the propagation dynamics of conventional Gaussian beams with initial angles have been widely studied. However, to our best knowledge, the propagation of the cone angle superimposed onto the novel CAB still remain unexplored. Therefore, it is interesting to investigate what will happen when a CAB with a cone angle is launched into a medium. The question is, how does the beam self-accelerate in this case? how do the properties of abruptly focus change under the action of the cone angle? In this paper, We will in detail reply these questions. Hence, the main aims of this paper is to present detailed investigation on abruptly focus of CCAB. In particular, we will try to disclose the novel behaviors different from those for the conventional CAB. 2. Theoretical model Here we consider the dynamical behaviors of a radially symmetric optical beam propagating in a linear medium. Under the paraxial approximation, the normalized equation for the evolution of slowly- varying envelope E of the optical electric field can be described by ⁎ Corresponding author. E-mail address: jgzhang007@163.com (J. Zhang). http://dx.doi.org/10.1016/j.optcom.2017.01.027 Received 31 August 2016; Received in revised form 15 January 2017; Accepted 17 January 2017 0030-4018/ © 2017 Published by Elsevier B.V. 

J. Zhang et al. E ∂ z ∂ = ⎛ ⎝⎜ i 2 E ∂ 2 r ∂ 2 E + 1 ∂ r r ∂ ⎞ ⎠⎟ , (1) where the radial coordinate r is normalized with respect to an arbitrary transverse length x0, z is the normalized propagation distance with respect to Rayleigh lengths. The dynamical behavior of an arbitrary radially symmetric initial condition E r( , 0) can be calculated according to the following forward Hankel transform: 0 0 ( ∞ ∫ /2) ik z 2 E k 0 E r z ( , J kr kdk 0 ( , 0)exp(− ) = 1 π 2 where J kr( ) is the zero-order Bessel function, k is the radial spatial 0 frequency. E k( , 0) is the Hankel transform of the input envelope E r( , 0) at z=0, and it can be obtained by applying the following 0 backward Hankel transform (2) ) , 0 E k 0 ( , 0) = 2 π ∞ ∫ 0 E r 0 ( , 0) J kr rdr 0 ( ) , (3) 0 r r ), ivr Ai r α r ( − )]exp( 0 ( , 0) = ( − )exp[ The initial envelope of electric fields of the CAB superimposed by a cone angle v (or “velocity”) in cylindrical coordinate can be written as [1,17] E r (4) 0 where r0 is the initial radius of the main ring and α is the decay factor. For r < r0, the energy of CCAB decays exponentially, while the slowly decaying oscillations of optical tail appear in the peripheral region. We first introduce the cone angle v into the CAB, which can provide an alternative approach to engineering the initial beams. In experiment, the actual cone angle θ is related to the normalized cone angle v through θ / 0 is the wavenumber of the optical wave, n is the refractive index and λ0 is the wavelength of optical wave. Therefore, in fact, the propagation properties of CCAB is controlled by the actual cone angle θ in experiment. In this paper, we will take some typical values of the parameters given as x μm , n=1.45, and λ . Based on the parameters, we easily obtain the actual cone angles θ belonging to different normalized cone angel v used in the following analysis, such as v ( = ± 1) ↔ ( = ± 0.0378 )° and v ( = ± 3) ↔ ( = ± 0.113 )° , Therefore, from the values, one find that the propagation properties of CCAB can be adjusted by only small actual cone angles in experiment. )0 where β = arcsin( / = 100 = 600 v x β πn λ = 2 nm θ θ 0 0 To explore the propagation properties of the CCAB, we will numerically compute the integral expression of CCAB in Eq. (2) in the later section since it is very difficult to obtain the accurate analytical solution to Eq. (2) under the initial condition given by Eq. (4). Here we will first derive an approximate analytical solution to help us more intuitively understand the unusual behavior of sharply autofocusing, as compared to the numerical method. As is well known, when the CAB is accelerated toward the beam axis, its radial profile over the transverse plane keeps almost constant along the whole moving trajectory until the focus is reached. Therefore, during the initial accelerated process, we take the approximation E r 2 in Eq. (1) since the second term on the right-hand side of Eq. (1) is not significant before focusing. Thus, substituting Eq. (4) into Eq. (1), we can obtain an approximate dynamics of CCAB through the method of Fourier transform as following E r z ( , ) = [− − /4 − /∂ + ∂ / ∂ ≈ ∂ E r r E r /∂ 2 ∂ 2 2 2 iαz ]exp[ r r − + ) /2 + (− + ) − 0 α (− + ) − ( z αz r 0 )/2 − ivz r iv r r 0 2 r Ai r 0 × exp[− /12 + ( − vz + i α 2 z 3 iz + v 2 αvz ] /2], 2 (5) Obviously, from Eq. (5), we easily find that CCAB accelerates in a fashion of a ballistic path in the r–z plane that is described by the following parabola r r + , = − /4 − 0 (6) vz z 2 Based on Eq. (6), we can further obtain the focal length of sharply autofocus by setting r=0 as following 117 Optics Communications 391 (2017) 116–120 z f = −2 + 2 v 2 v + , 0 r (7) Eqs. (6)–(7) is our central result of analytical expression to this research, being the closed-form approximation. Obviously, some qualitative physical insight related with the trajectory and the focal length can be directly gained from Eqs. (6)–(7) even without numerical calculation. For example, the focal length zf decreases monotonically as increasing the value of v for v > 0; while it increases monotonically as increasing absolute value of v for v < 0. In addition, one notes that the focal length zf will increases monotonically with the increase of r0. Here, we need to stress that the trajectory in Eq. (6) and the focal length in Eq. (7) are somewhat rude approximations, because we omitted the first term on the right-hand side of Eq. (1) during the process of the derivation. However, the accurate numerical solution based on the Hankel transform will be employed to check the validity of our analytical prediction in the next section. In addition, here we have to mention that Eqs. (6) and (7) is only suitable for describing the dynamical behavior of CCAB before focusing. Therefore, after the main lobe of CCAB is close to the axis through self-acceleration, i.e., when the behavior of focus begins to occur, the approximate condition used in deriving Eqs. (6) and (7) is not tenable. As a consequence, our analytical model cannot predict the dynamical behavior of rapid increase of optical intensity near focal point, which will be investigated by employing the numerical method in the next section. 3. Results and discussions In this section, we will in detail discuss the propagation properties of the CCAB beams. We note that the accurate analytical expression of Hankel transform for CAB is not derived by substituting Eqs. (3) and (4) into Eq. (2). To investigate the propagation properties of CCAB, we will employ the well-known quasi-discrete method proposed provided by Guizar-Sicairos et al. to numerically compute the integral expression in Eq. (2) [18]. This numerical approach is found to be much more efficient and accurate than other existing approaches. In the following analysis, we assume α = 0.2 and r0=8 unless otherwise specified. We first discuss the properties of focal position as well as the focal trajectory during the evolution process of sharply autofocusing beam. 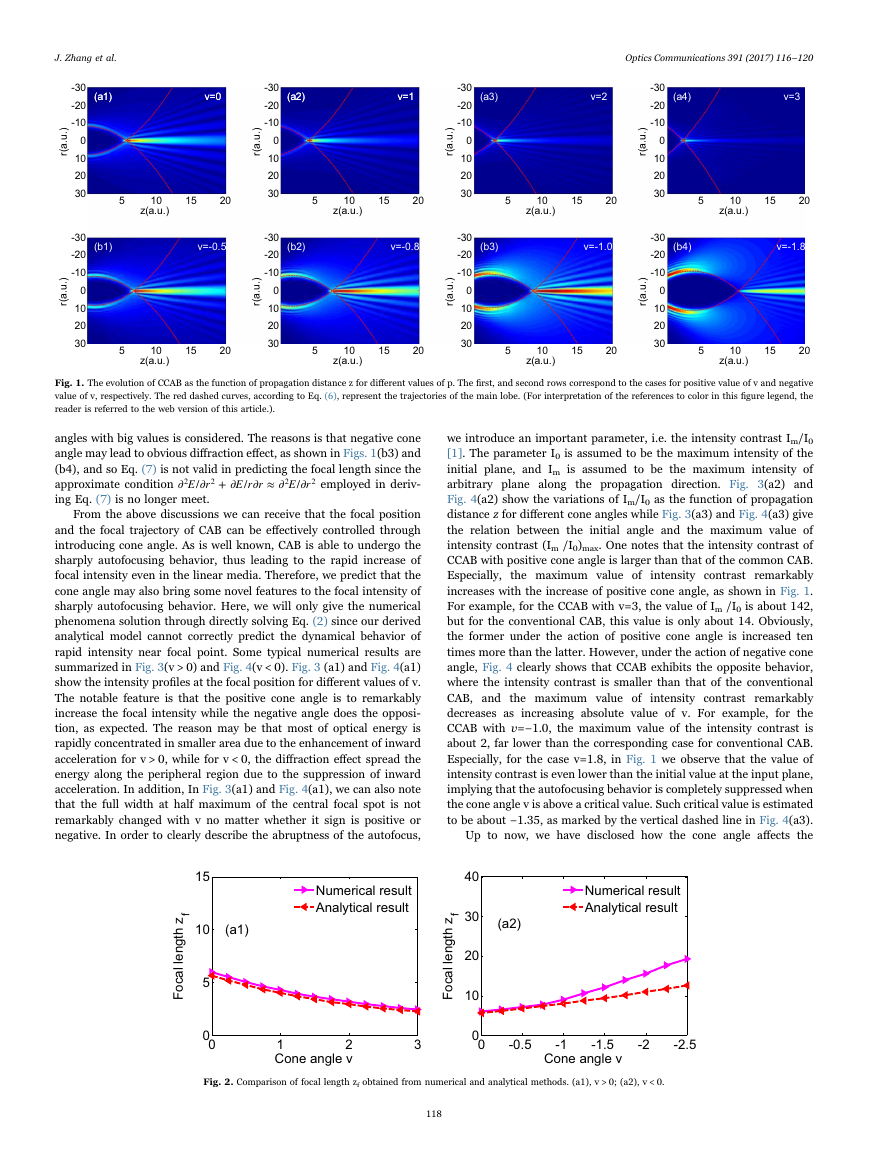The simulation results are shown in Fig. 1 were we plot the evolution of CCAB as the function of propagation distance z under the action of different values of v. In order to compare with the theoretical prediction more clearly, we also display the analytical accelerating trajectories of the main lobes of CCAB marked by red dashed cureve in Fig. 1, according to Eq. (6). When the CCAB is launched with a positive cone angle (v > 0), the direction of the initial velocity related with cone angle is in the same direction as the original self-acceleration, and so the beam still perform self-acceleration during propagation. However, the extent of self-acceleration is greatly strengthened and the focal length is remarkably reduced. When the CAB is launched with a negative cone angle (v < 0), the direction of the initial velocity related with cone angle is opposite to that of the original self-acceleration. Therefore, the self-acceleration of optical beam is prevented, and the CCAB may first perform deceleration and then acceleration during propagation. Accordingly, the autofocusing effect may be weakened and the focal length is largely extended. From Fig. 1, we can clearly see that the theoretical prediction is in accordance with numerical simula- tions. 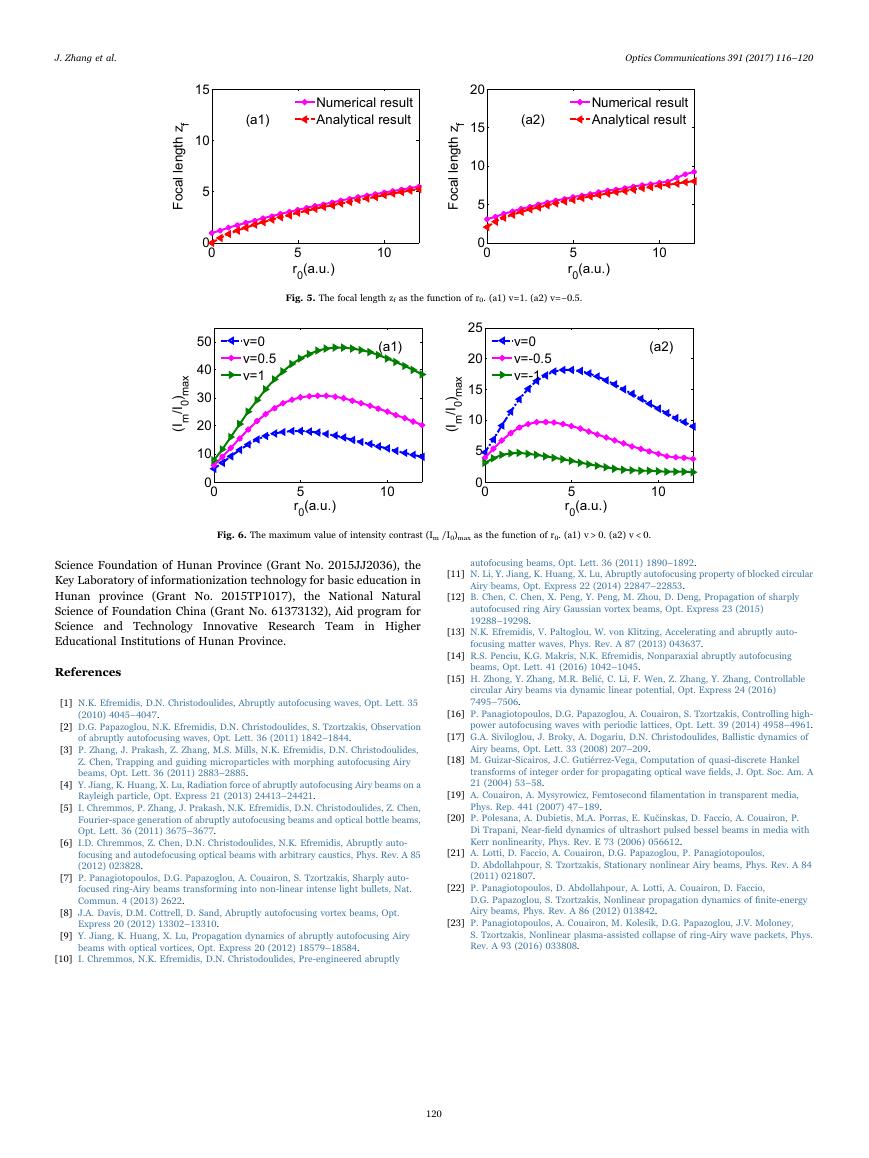Besides, in order to analyze the accelerating process more clearly, we also present a comparison of focal length zf obtained from analytical and numerical methods in Fig. 2. Here, the analytical focal length zf comes from our derived Eq. (7), while the numerical focal length zf is defined as the distance from the input point to the point at which the maximum peak intensity occurs. Obviously, the analytical and numer- ical lengths are in good qualitative agreement each other. Meanwhile, one notes that small differences between the results obtained by direct simulations as well as investigations based on Eq. (7) are also observed, especially for the case when negative incident focal 

J. Zhang et al. Optics Communications 391 (2017) 116–120 ) . u . a ( r ) . u . a ( r -30 -20 -10 0 10 20 30 -30 -20 -10 0 10 20 30 (a1) (a1) v=0 v=0 5 10 z(a.u.) 15 20 (b1) v=-0.5 5 10 z(a.u.) 15 20 ) . u . a ( r ) . u . a ( r -30 -20 -10 0 10 20 30 -30 -20 -10 0 10 20 30 (a2) (a2) v=1 v=1 5 10 z(a.u.) 15 20 (b2) v=-0.8 5 10 z(a.u.) 15 20 ) . u . a ( r ) . u . a ( r -30 -20 -10 0 10 20 30 -30 -20 -10 0 10 20 30 (a3) v=2 5 10 z(a.u.) 15 20 (b3) v=-1.0 5 10 z(a.u.) 15 20 ) . u . a ( r ) . u . a ( r -30 -20 -10 0 10 20 30 -30 -20 -10 0 10 20 30 (a4) v=3 5 10 z(a.u.) 15 20 (b4) v=-1.8 5 10 z(a.u.) 15 20 Fig. 1. The evolution of CCAB as the function of propagation distance z for different values of p. The first, and second rows correspond to the cases for positive value of v and negative value of v, respectively. The red dashed curves, according to Eq. (6), represent the trajectories of the main lobe. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.). angles with big values is considered. The reasons is that negative cone angle may lead to obvious diffraction effect, as shown in Figs. 1(b3) and (b4), and so Eq. (7) is not valid in predicting the focal length since the approximate condition E r 2 employed in deriv- ing Eq. (7) is no longer meet. /∂ + ∂ / ∂ ≈ ∂ E r r E r /∂ 2 2 ∂ 2 From the above discussions we can receive that the focal position and the focal trajectory of CAB can be effectively controlled through introducing cone angle. As is well known, CAB is able to undergo the sharply autofocusing behavior, thus leading to the rapid increase of focal intensity even in the linear media. Therefore, we predict that the cone angle may also bring some novel features to the focal intensity of sharply autofocusing behavior. Here, we will only give the numerical phenomena solution through directly solving Eq. 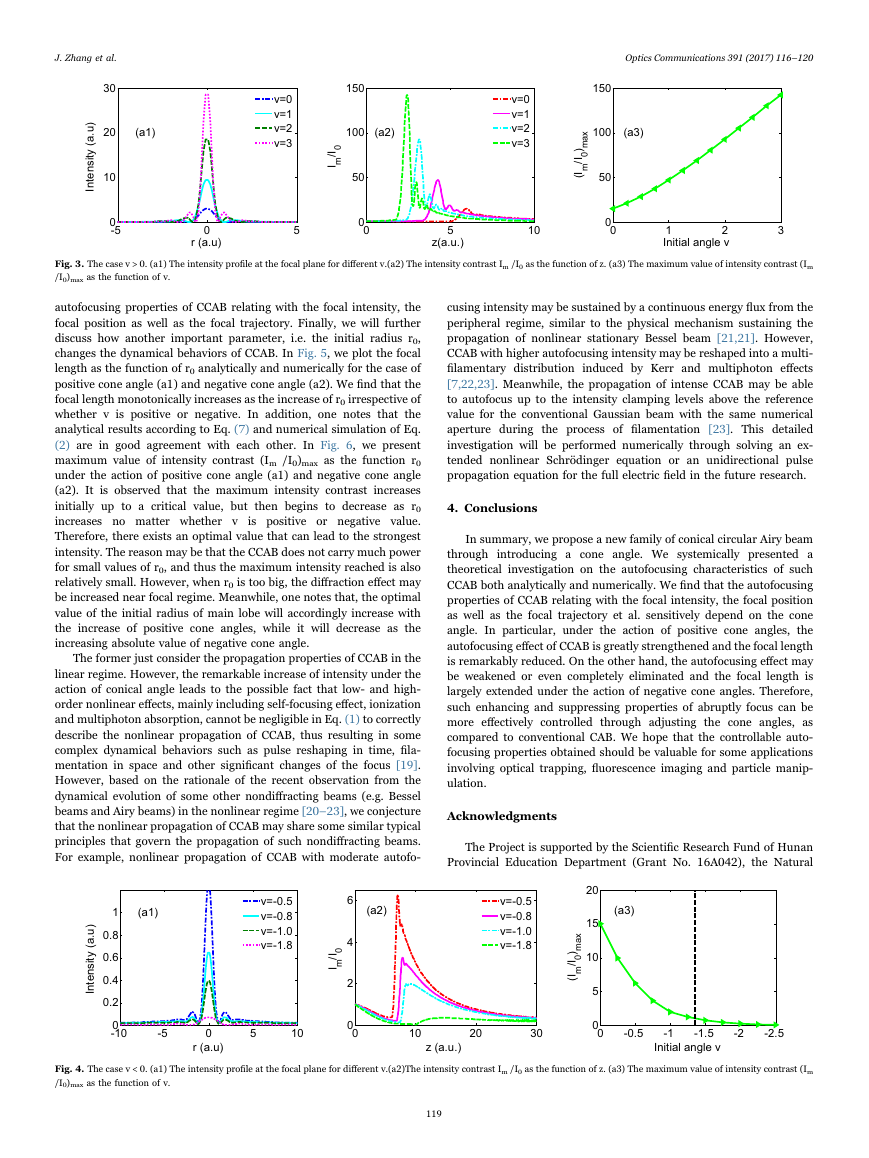(2) since our derived analytical model cannot correctly predict the dynamical behavior of rapid intensity near focal point. Some typical numerical results are summarized in Fig. 3(v > 0) and Fig. 4(v < 0). Fig. 3 (a1) and Fig. 4(a1) show the intensity profiles at the focal position for different values of v. The notable feature is that the positive cone angle is to remarkably increase the focal intensity while the negative angle does the opposi- tion, as expected. The reason may be that most of optical energy is rapidly concentrated in smaller area due to the enhancement of inward acceleration for v > 0, while for v < 0, the diffraction effect spread the energy along the peripheral region due to the suppression of inward acceleration. In addition, In Fig. 3(a1) and Fig. 4(a1), we can also note that the full width at half maximum of the central focal spot is not remarkably changed with v no matter whether it sign is positive or negative. In order to clearly describe the abruptness of the autofocus, the maximum value of we introduce an important parameter, i.e. the intensity contrast Im/I0 [1]. The parameter I0 is assumed to be the maximum intensity of the initial plane, and Im is assumed to be the maximum intensity of arbitrary plane along the propagation direction. Fig. 3(a2) and Fig. 4(a2) show the variations of Im/I0 as the function of propagation distance z for different cone angles while Fig. 3(a3) and Fig. 4(a3) give the relation between the initial angle and the maximum value of intensity contrast (Im /I0)max. One notes that the intensity contrast of CCAB with positive cone angle is larger than that of the common CAB. Especially, intensity contrast remarkably increases with the increase of positive cone angle, as shown in Fig. 1. For example, for the CCAB with v=3, the value of Im /I0 is about 142, but for the conventional CAB, this value is only about 14. Obviously, the former under the action of positive cone angle is increased ten times more than the latter. However, under the action of negative cone angle, Fig. 4 clearly shows that CCAB exhibits the opposite behavior, where the intensity contrast is smaller than that of the conventional CAB, and the maximum value of intensity contrast remarkably decreases as increasing absolute value of v. For example, for the CCAB with v=−1.0, the maximum value of the intensity contrast is about 2, far lower than the corresponding case for conventional CAB. Especially, for the case v=1.8, in Fig. 1 we observe that the value of intensity contrast is even lower than the initial value at the input plane, implying that the autofocusing behavior is completely suppressed when the cone angle v is above a critical value. Such critical value is estimated to be about −1.35, as marked by the vertical dashed line in Fig. 4(a3). Up to now, we have disclosed how the cone angle affects the f z h t g n e l l a c o F 15 10 (a1) 5 0 0 Numerical result Analytical result (a2) 40 30 20 10 f z h t g n e l l a c o F Numerical result Analytical result 1 2 Cone angle v 3 0 0 -0.5 -1 -1.5 Cone angle v -2 -2.5 Fig. 2. Comparison of focal length zf obtained from numerical and analytical methods. (a1), v > 0; (a2), v < 0. 118 

J. Zhang et al. 30 ) u . a ( y t i s n e t n I 20 (a1) 10 0 -5 Optics Communications 391 (2017) 116–120 v=0 v=1 v=2 v=3 0 r (a.u) 5 150 100 (a2) 0 I / m I 50 0 0 v=0 v=1 v=2 v=3 5 z(a.u.) 10 x a m 0 ) I / m I ( 150 100 (a3) 50 0 0 1 2 Initial angle v 3 Fig. 3. The case v > 0. (a1) The intensity profile at the focal plane for different v.(a2) The intensity contrast Im /I0 as the function of z. (a3) The maximum value of intensity contrast (Im /I0)max as the function of v. autofocusing properties of CCAB relating with the focal intensity, the focal position as well as the focal trajectory. Finally, we will further discuss how another important parameter, i.e. the initial radius r0, changes the dynamical behaviors of CCAB. In Fig. 5, we plot the focal length as the function of r0 analytically and numerically for the case of positive cone angle (a1) and negative cone angle (a2). We find that the focal length monotonically increases as the increase of r0 irrespective of whether v is positive or negative. In addition, one notes that the analytical results according to Eq. (7) and numerical simulation of Eq. (2) are in good agreement with each other. In Fig. 6, we present maximum value of intensity contrast (Im /I0)max as the function r0 under the action of positive cone angle (a1) and negative cone angle (a2). It is observed that the maximum intensity contrast increases initially up to a critical value, but then begins to decrease as r0 increases no matter whether v is positive or negative value. Therefore, there exists an optimal value that can lead to the strongest intensity. The reason may be that the CCAB does not carry much power for small values of r0, and thus the maximum intensity reached is also relatively small. However, when r0 is too big, the diffraction effect may be increased near focal regime. Meanwhile, one notes that, the optimal value of the initial radius of main lobe will accordingly increase with the increase of positive cone angles, while it will decrease as the increasing absolute value of negative cone angle. The former just consider the propagation properties of CCAB in the linear regime. However, the remarkable increase of intensity under the action of conical angle leads to the possible fact that low- and high- order nonlinear effects, mainly including self-focusing effect, ionization and multiphoton absorption, cannot be negligible in Eq. (1) to correctly describe the nonlinear propagation of CCAB, thus resulting in some complex dynamical behaviors such as pulse reshaping in time, fila- mentation in space and other significant changes of the focus [19]. However, based on the rationale of the recent observation from the dynamical evolution of some other nondiffracting beams (e.g. Bessel beams and Airy beams) in the nonlinear regime [20–23], we conjecture that the nonlinear propagation of CCAB may share some similar typical principles that govern the propagation of such nondiffracting beams. For example, nonlinear propagation of CCAB with moderate autofo- cusing intensity may be sustained by a continuous energy flux from the peripheral regime, similar to the physical mechanism sustaining the propagation of nonlinear stationary Bessel beam [21,21]. However, CCAB with higher autofocusing intensity may be reshaped into a multi- filamentary distribution induced by Kerr and multiphoton effects [7,22,23]. Meanwhile, the propagation of intense CCAB may be able to autofocus up to the intensity clamping levels above the reference value for the conventional Gaussian beam with the same numerical aperture during the process of filamentation [23]. This detailed investigation will be performed numerically through solving an ex- tended nonlinear Schrödinger equation or an unidirectional pulse propagation equation for the full electric field in the future research. 4. Conclusions In summary, we propose a new family of conical circular Airy beam through introducing a cone angle. We systemically presented a theoretical investigation on the autofocusing characteristics of such CCAB both analytically and numerically. We find that the autofocusing properties of CCAB relating with the focal intensity, the focal position as well as the focal trajectory et al. sensitively depend on the cone angle. In particular, under the action of positive cone angles, the autofocusing effect of CCAB is greatly strengthened and the focal length is remarkably reduced. On the other hand, the autofocusing effect may be weakened or even completely eliminated and the focal length is largely extended under the action of negative cone angles. Therefore, such enhancing and suppressing properties of abruptly focus can be more effectively controlled through adjusting the cone angles, as compared to conventional CAB. We hope that the controllable auto- focusing properties obtained should be valuable for some applications involving optical trapping, fluorescence imaging and particle manip- ulation. Acknowledgments The Project is supported by the Scientific Research Fund of Hunan Provincial Education Department (Grant No. 16A042), the Natural v=-0.5 v=-0.8 v=-1.0 v=-1.8 (a1) ) u . a ( y t i s n e t n I 1 0.8 0.6 0.4 0.2 0 -10 -5 0 r (a.u) 5 10 (a2) 0 I / m I 6 4 2 0 0 v=-0.5 v=-0.8 v=-1.0 v=-1.8 10 z (a.u.) 20 30 x a m 0 ) I / m I ( 20 15 10 5 0 0 (a3) -0.5 -1 -1.5 Initial angle v -2 -2.5 Fig. 4. The case v < 0. (a1) The intensity profile at the focal plane for different v.(a2)The intensity contrast Im /I0 as the function of z. (a3) The maximum value of intensity contrast (Im /I0)max as the function of v. 119 

J. Zhang et al. Optics Communications 391 (2017) 116–120 f z h t g n e l l a c o F x a m 0 ) I / m I ( 15 10 5 0 0 50 40 30 20 10 0 0 (a1) Numerical result Analytical result 20 f z 15 h t g n e l l a c o F 10 5 (a2) Numerical result Analytical result 10 5 r0(a.u.) Fig. 5. The focal length zf as the function of r0. (a1) v=1. (a2) v=−0.5. 5 r0(a.u.) 0 0 10 (a2) v=0 v=0.5 v=1 (a1) 5 r0(a.u.) 10 v=0 v=-0.5 v=-1 x a m 0 ) I / m I ( 25 20 15 10 5 0 0 5 r0(a.u.) 10 Fig. 6. The maximum value of intensity contrast (Im /I0)max as the function of r0. (a1) v > 0. (a2) v < 0. Science Foundation of Hunan Province (Grant No. 2015JJ2036), the Key Laboratory of informationization technology for basic education in Hunan province (Grant No. 2015TP1017), the National Natural Science of Foundation China (Grant No. 61373132), Aid program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province. autofocusing beams, Opt. Lett. 36 (2011) 1890–1892. [11] N. Li, Y. Jiang, K. Huang, X. Lu, Abruptly autofocusing property of blocked circular Airy beams, Opt. Express 22 (2014) 22847–22853. [12] B. Chen, C. Chen, X. Peng, Y. Peng, M. Zhou, D. Deng, Propagation of sharply autofocused ring Airy Gaussian vortex beams, Opt. Express 23 (2015) 19288–19298. [13] N.K. Efremidis, V. Paltoglou, W. von Klitzing, Accelerating and abruptly auto- focusing matter waves, Phys. Rev. A 87 (2013) 043637. [14] R.S. Penciu, K.G. Makris, N.K. Efremidis, Nonparaxial abruptly autofocusing beams, Opt. Lett. 41 (2016) 1042–1045. [15] H. Zhong, Y. Zhang, M.R. Belić, C. Li, F. Wen, Z. Zhang, Y. Zhang, Controllable circular Airy beams via dynamic linear potential, Opt. Express 24 (2016) 7495–7506. [16] P. Panagiotopoulos, D.G. Papazoglou, A. Couairon, S. Tzortzakis, Controlling high- power autofocusing waves with periodic lattices, Opt. Lett. 39 (2014) 4958–4961. [17] G.A. Siviloglou, J. Broky, A. Dogariu, D.N. Christodoulides, Ballistic dynamics of Airy beams, Opt. Lett. 33 (2008) 207–209. [18] M. Guizar-Sicairos, J.C. Gutiérrez-Vega, Computation of quasi-discrete Hankel transforms of integer order for propagating optical wave fields, J. Opt. Soc. Am. A 21 (2004) 53–58. [19] A. Couairon, A. Mysyrowicz, Femtosecond filamentation in transparent media, Phys. Rep. 441 (2007) 47–189. [20] P. Polesana, A. Dubietis, M.A. Porras, E. Kučinskas, D. Faccio, A. Couairon, P. Di Trapani, Near-field dynamics of ultrashort pulsed bessel beams in media with Kerr nonlinearity, Phys. Rev. E 73 (2006) 056612. [21] A. Lotti, D. Faccio, A. Couairon, D.G. Papazoglou, P. Panagiotopoulos, D. Abdollahpour, S. Tzortzakis, Stationary nonlinear Airy beams, Phys. Rev. A 84 (2011) 021807. [22] P. Panagiotopoulos, D. Abdollahpour, A. Lotti, A. Couairon, D. Faccio, D.G. Papazoglou, S. Tzortzakis, Nonlinear propagation dynamics of finite-energy Airy beams, Phys. Rev. A 86 (2012) 013842. [23] P. Panagiotopoulos, A. Couairon, M. Kolesik, D.G. Papazoglou, J.V. Moloney, S. Tzortzakis, Nonlinear plasma-assisted collapse of ring-Airy wave packets, Phys. Rev. A 93 (2016) 033808. References [1] N.K. Efremidis, D.N. Christodoulides, Abruptly autofocusing waves, Opt. Lett. 35 (2010) 4045–4047. [2] D.G. Papazoglou, N.K. Efremidis, D.N. Christodoulides, S. Tzortzakis, Observation of abruptly autofocusing waves, Opt. Lett. 36 (2011) 1842–1844. [3] P. Zhang, J. Prakash, Z. Zhang, M.S. Mills, N.K. Efremidis, D.N. Christodoulides, Z. Chen, Trapping and guiding microparticles with morphing autofocusing Airy beams, Opt. Lett. 36 (2011) 2883–2885. [4] Y. Jiang, K. Huang, X. Lu, Radiation force of abruptly autofocusing Airy beams on a Rayleigh particle, Opt. Express 21 (2013) 24413–24421. [5] I. Chremmos, P. Zhang, J. Prakash, N.K. Efremidis, D.N. Christodoulides, Z. Chen, Fourier-space generation of abruptly autofocusing beams and optical bottle beams, Opt. Lett. 36 (2011) 3675–3677. [6] I.D. Chremmos, Z. Chen, D.N. Christodoulides, N.K. Efremidis, Abruptly auto- focusing and autodefocusing optical beams with arbitrary caustics, Phys. Rev. A 85 (2012) 023828. [7] P. Panagiotopoulos, D.G. Papazoglou, A. Couairon, S. Tzortzakis, Sharply auto- focused ring-Airy beams transforming into non-linear intense light bullets, Nat. Commun. 4 (2013) 2622. [8] J.A. Davis, D.M. Cottrell, D. Sand, Abruptly autofocusing vortex beams, Opt. Express 20 (2012) 13302–13310. [9] Y. Jiang, K. Huang, X. Lu, Propagation dynamics of abruptly autofocusing Airy beams with optical vortices, Opt. Express 20 (2012) 18579–18584. [10] I. Chremmos, N.K. Efremidis, D.N. Christodoulides, Pre-engineered abruptly 120