2007并行程序设计期末考试卷.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.13M 资料格式：pdf 举报版权申诉

yzh168yzh-8254455-4744300845375839315.pdf-第1页.png

第1页 / 共6页

yzh168yzh-8254455-4744300845375839315.pdf-第2页.png

第2页 / 共6页

yzh168yzh-8254455-4744300845375839315.pdf-第3页.png

第3页 / 共6页

yzh168yzh-8254455-4744300845375839315.pdf-第4页.png

第4页 / 共6页

yzh168yzh-8254455-4744300845375839315.pdf-第5页.png

第5页 / 共6页

yzh168yzh-8254455-4744300845375839315.pdf-第6页.png

第6页 / 共6页

文本预览

中国科学技术大学 2007－2008 学年第一学期考试试卷《并行程序设计》期末考试参考解答一、针对以下循环，（20 分）（1）描述此循环中依赖关系和迭代依赖图；（2）给出并行化此循环的两种方案，并比较它们的并行粒度。 for( i=0;i<10;i++) for(j=0;j<10;j++) a[i][j] = ( a[i-1][j] + a[i+1][j]) / 2; 参考解答：（1）依赖关系：此循环中存在依赖向量为(1，0)的 SδfS 流依赖关系和依赖向量为（1， 0）的 SδaS 反依赖关系。 for( i=0;i<10;i++) for(j=0;j<10;j++) S： a[i][j] = ( a[i-1][j] + a[i+1][j]) / 2; 迭代依赖图如下：（2）此循环并行化可以参考如下两种方案：方案 1：直接并行化内层循环。内层循环满足循环并行化条件（不存在由该层携带的依赖关系）；但这样的并行化的粒度仅为一条语句，即语句 S。方案 2：采用循环交换的程序变换。原程序变换为，

for(j=0;j<10;j++) for( i=0;i<10;i++) S： a[i][j] = ( a[i-1][j] + a[i+1][j]) / 2; 其依赖向量为（0，1），可以将外层 j 循环直接并行化。这样，并行化的粒度就是内层整个 i 循环。二、以下 OpenMP 程序不能正确工作（线程总数大于 1），请给出两种解决方案。（20 分） #pragma omp for private(i,j) for( i=0;i<100;i++) for(j=0;j<10;j++) a[i][j] = a[i-1][j+1] ; 参考解答：该循环存在着依赖向量为（1，-1）的流依赖关系。根据循环并行化条件，不能直接并行化外层 i 循环。有两种解决方案可以使用：方案一：将原来对外层 i 循环的并行化改为对内层 j 循环的并行化（内层 j 循环满足循环并行化条件）；但此时并行化的只是内层 j 循环的 10 次迭代。修改后的程序如下： for( i=0;i<100;i++){ #pragma omp for private(j) for(j=0;j<10;j++) a[i][j] = a[i-1][j+1] ; } 方案二：先对内层 j 循环采用循环逆转变换，此时，循环依赖向量为（1，1），然后在进行内外层循环交换的程序变换，这样可以将内层 i 循环并行化。对比方案一，此时可并行化的是内层 i 循环的 100 次迭代。变换后程序如下： for( j=9;j>=0;j--){ #pragma omp for private(i) for(i=0;i<100;i++) a[i][j] = a[i-1][j+1] ; } 2007－2008 学年第一学期《并行程序设计》期末考试第 1 页(共 1 页)

三、在以下 MPI 程序片段中，矩阵 A 被划分为 5X5 的子矩阵，并由 rank 为 0 的进程将子矩阵发送给所有进程中的矩阵 B（如图 1 所示，Pi 表示第 i 个进程）；请补全此程序中划线部分的代码，并给出 rank 为 0 的进程接收所有进程中的矩阵 B 而重新建立矩阵 A 的代码。 P0 P4 P8 P1 P5 P9 P2 P6 P3 P7 P10 P11 P12 P13 P14 P15 图 1 子矩阵分布图（20 分） double A[20][20], B[5][5]; MPI_Datatype SubMatrix_5X5; MPI_Type_vector( , , , MPI_DOUBLE, &SubMatrix_5X5); MPI_Type_commit(&SubMatrix_5X5); // 发送子矩阵 if(rank == 0) // rank 为进程号 for(i=0;i

for (i=1; i(iter-M) ) { //每个线程计算自己的第一个元素的值 if (thread != 0) a[limitL] = ( a[limitL] + border ) / 2; //计算剩余元素的值 for (i=limitL+1; i<=limitR; i++) a[i] = ( a[i] + a[i-1] ) / 2; } // end of if // 拷贝已更新的边界数据前，所有线程再次同步 #pragma omp barrier } // for 循环结束 } // 并行区域结束 2007－2008 学年第一学期《并行程序设计》期末考试第 1 页(共 1 页)

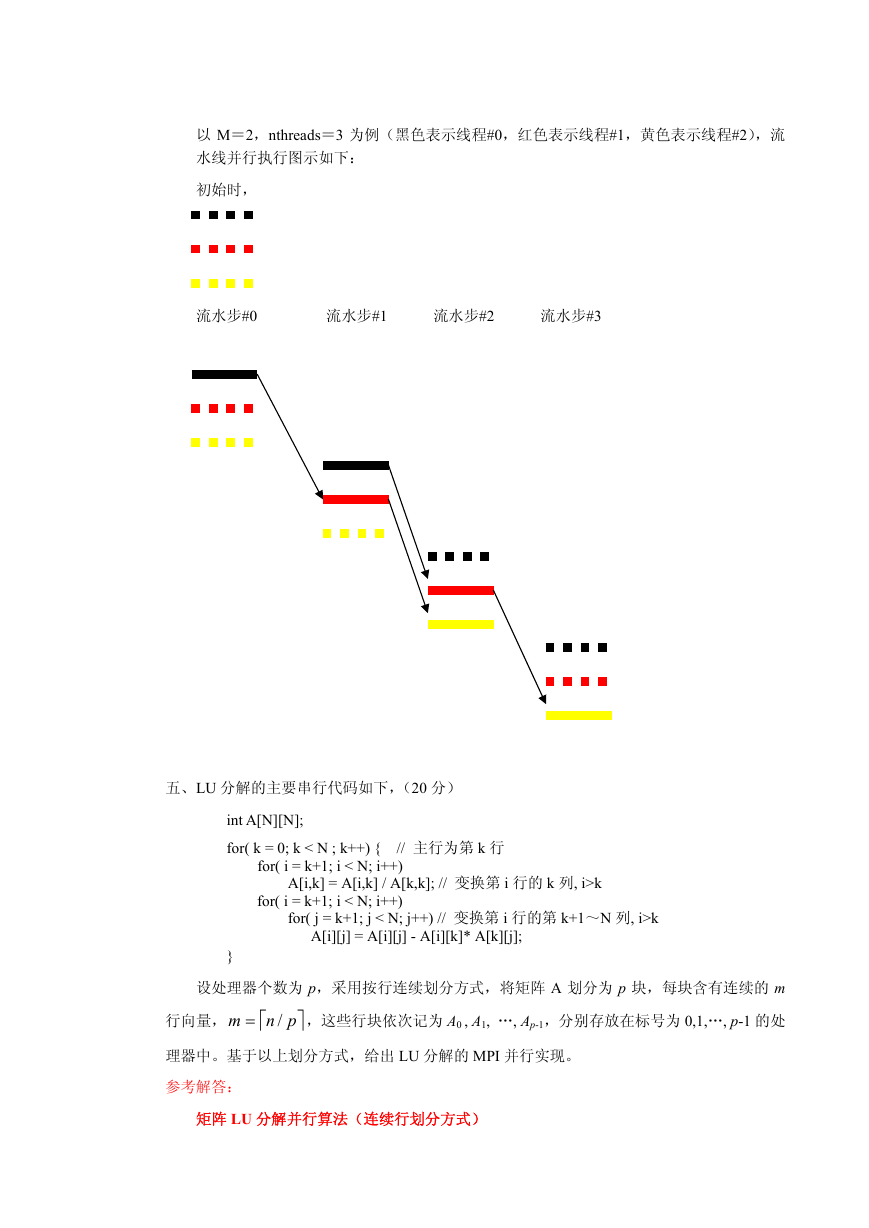
以 M＝2，nthreads＝3 为例（黑色表示线程#0，红色表示线程#1，黄色表示线程#2），流水线并行执行图示如下：初始时，流水步#0 流水步#1 流水步#2 流水步#3 五、LU 分解的主要串行代码如下，（20 分） int A[N][N]; for( k = 0; k < N ; k++) { // 主行为第 k 行 for( i = k+1; i < N; i++) A[i,k] = A[i,k] / A[k,k]; // 变换第 i 行的 k 列, i>k for( i = k+1; i < N; i++) for( j = k+1; j < N; j++) // 变换第 i 行的第 k+1～N 列, i>k A[i][j] = A[i][j] - A[i][k]* A[k][j]; } 设处理器个数为 p，采用按行连续划分方式，将矩阵 A 划分为 p 块，每块含有连续的 m 行向量， ⎤pnm = ⎡ / ，这些行块依次记为 A0 , A1, …, Ap-1，分别存放在标号为 0,1,…, p-1 的处理器中。基于以上划分方式，给出 LU 分解的 MPI 并行实现。参考解答：矩阵 LU 分解并行算法（连续行划分方式）

输入：矩阵 An×n，输出：矩阵 Ln×n，矩阵 Un×n Begin 对所有处理器 my_rank(my_rank=0,…, p-1)同时执行如下的算法: (1)if (my_rank=0) then /*0 号处理器*/ (1.1)for j=0 to m-2 do 将第 j 行作为主行，（绝对行号为 Z=m*myrank+j)；并发送给其他所有 rank>myrank 的处理器； for i=j+1 to m-1 do 以第 j 行为主行，变换第 i 行； end for end for (1.2)将变换后的第 m-1 行作为主行发送到其他所有 rank>myrank 处理器 end if (2)if ((my_rank>0) and (my_rank<(p-1))) then /*中间处理器*/ (2.1) for j=0 to my_rank*m-1 do (i)接收 rankmyrank 的处理器； for i=j+1 to m-1 do 以第 j 行为主行，变换第 i 行； end for end for (2.3)将变换后的第 m-1 行传送到其他所有 rank>myrank 的处理器 end if (3)if (my_rank= (p-1)) then /*p-1 号处理器*/ (3.1) for j=0 to my_rank*m-1 do (i)接收 rank

分享到：

赞收藏

资料库

2007并行程序设计期末考试卷.pdf

相关推荐

开发技术

热门标签

最新资料