第1页 / 共23页
第2页 / 共23页
第3页 / 共23页
第4页 / 共23页
第5页 / 共23页
第6页 / 共23页
第7页 / 共23页
第8页 / 共23页
通信网理论基础 课后答案.doc
3.4
3.5 试求图3-52中图的主树数目，并列举所有的主树。
3.6 试证明端数n大于4的连接图都是非平面图，并求n=2，3，4的全连接图为对偶图。
3.7
3.8 图有六个端，其无向距离矩阵如下：
3.9 图有六个端，端点之间的有向距离矩阵如下：
3.11求下图中Vs到Vt的最大流量fst,图中编上的数字是该边的容量。
3.12试移动3.54图中的一条边，保持其容量不变，是否能增大fst？如果可以，求此时的最大值，但若
3.13图3.55中的Vs和Vt间要求有总流量fst＝6，求最佳流量分配，图中边旁的两个数字前者为容
3.16试计算完全图Kn的主树的数目。
4.1 求M/M/m（n）中，等待时间w的概率密度函数。
4.4求M/D/1排队问题中等待时间W的一、二、三阶矩m1、m2、m3，D表示服务时间为定值b，到达
4.5 求M/B/1，B/M/1和B/B/1排队问题的平均等待时间
4.6 在D/D/1排队问题中，顾客到达的时间间隔为a，服务时间为b，均为恒定值，且a>b，
4.8在优先级别队列中，A队为优先级，不拒绝，B队为非优先级，只准一人排队等待（不计在服务中的），且
4.9排队系统中有三个队列,其到达率分别为公用同一出线
4.10 有一个三端网络，端点为，边为
4.12在分组交换系统中，设信息包以泊松率到达，平均到达率为，但信息包的长度为固定b比特，信道容量
4.13有四个端三条边组成的数据网，如图所示。端间的信息包分别为和每秒，信息包长度为负指数分布，平均
4.14总线上有4个用户v1,v2,v3和v4，它们之间以Alopha方式互相通信，信包到达率均为每
3.4
1. 环上有 k 个端（3≤k≤n），此 k 个端的选择方式有 k
nC 种；对于某固定的 k 端来说，考
虑可以生成的环，任指定一个端，下个端的选取方法公有 k-1 种，再下端的选法有 k-2
种，等等，注意，这样生成的环可按两种试图顺序取得，故有
)!1
( k
2
种，总的环数为
n
k
3
(
kC
k
n
)!1
2
2. 某一固定边 e 确定了两个端，经过 e 的环数按其过余下端进行分类，若环再过 k 个端（1
≤k≤n-2），有选法 k
nC 2 种；对于某固定端来说，自然可以生成 k!个环，从而总的环
n
数为
k
3
k
n kC
2 ! 个。
3. 两个固定端之间的径按其经过端数分类，其中有一条不经过其他端的径，若经过 k 个端，
（1≤k≤n-2），则对于第一个端有（n-2）种选择，第二个端有（n-3）种选择，第 k
个端有（n-k-1）种选择，共有
(
n
(
)!2
n
k
)!2
总的径数为
1
n
2
k
1
(
n
(
)!2
n
k
)!2
3.5 试求图 3-52 中图的主树数目，并列举所有的主树。
解：为图的端编号为 v1,v2,v3,v4。
取 v3 为参考点，有：
3
1
1
1
2
0
1
0
2
8
S
图 3-52
所得主树见下:
第 1 页 共 23 页
3.6 试证明端数 n 大于 4 的连接图都是非平面图，并求 n=2，3，4 的全连接图为对偶图。
证明：设有 n 个端的全联接图为 Kn 因为 K5 是非平面图，而当 n>5 时 K5 是 Kn 的子图，从而 Kn
（n>5）均不是平面图。一下是对偶图（注意 K4 为自对偶图）。
3.7
C
0
0
0
0
1
0
0
0
0
1
0
0
1
0
1
0
解：首先作出图形：
已知一个图的邻接矩阵如左，画出此图，并求各
端之间的最小有向径长。
对所绘制图形的端点进行编号，得邻接矩阵。
v
2
3
v
v
0101
0100
1000
0000
4
C
v
1
第 2 页 共 23 页
经计算：
2C
0100
1000
0000
0000
3C
1000
0000
0000
0000
因而有
,
(
vvd
1
2
)
1
,
(
vvd
1
3
)
2
,
(
vvd
1
4
)
1
,
(
vvd
2
3
)
1
,
(
vvd
2
4
)
2
,
(
vvd
3
4
)
1
其余有向径长均为 ∞，或不存在。
3.8 图有六个端，其无向距离矩阵如下：
v
1
v
v
v
v
v
v
1
2
3
4
5
6
2
3
4
5
v
v
v
v
123210
232101
321012
210123
101232
021321
1. 用 P 算法，求出最短树。
2. 用 K 算法，求出最短树。
3. 限制条件为两端间通信的转接次数不超过 2 的最
短树。
6
v
解：
1.
P 算法求解：
,
,
vv
v
vvv
1
1
4
,
,
,
,
vvvvvv
1
2
,
e
12
,
34
23
5
6
3
2
1
2
e
e
3
e
16
,
vvvv
1
,
,
3
2
6
e
,
vvvvv
1
,
,
,
65
6
3
2
5
2.
K 算法求解：
按最小边长顺序取得：
e
12
e
23
e
34
e
45
e
56
1
此结果意味着最短树不唯一。
第 3 页 共 23 页
3. 原图有一个边长全为 1 的基本子图 G1，要求转接次数小于等于 2，若选取 G1 的任何 4 个
4v 为基
,作为基础，然后再按要求增加边，例如以 1v
连续顶点， iv
2iv
3iv
1iv
2v
3v
础，增加 5v
6v ，得到一个树长为 7 转接次数小于等于 2 的树 T1，事实上，以任何 4 个
连续顶点均可得到树长为 7 的转接次数小于等于 2 的树
3.9 图有六个端，端点之间的有向距离矩阵如下：
v
1
v
v
v
v
v
v
1
2
3
4
5
6
v
2
9
0
1
0
2
6
7
1. 用 D 算法求 V1 到所有其他端的最短径长及其路径。
2. 用 F 算法求最短径矩阵和路由矩阵，并找到 V2 至 V4
和 V1 至 V5 的最短径长及路由。
3. 求图的中心和中点。
v
3
1
4
0
5
2
2
v
4
3
0
8
v
v
5
6
7
1
2
7
0
5
2
0
解：
1.
V1
0
D 算法
V2
∞
9
9
8
8
8
V3
∞
1
V4
∞
3
3
3
V5
∞
∞
2
V6
∞
∞
∞
7
7
指定
最短径长
V1
V3
V5
V4
V3
V2
W1＝0
W13＝0
W15＝0
W14＝0
W16＝0
W12＝0
2.
F 算法
最短路径矩阵及最短路由阵为 W5，R5
v
2
v
1
v
4
有向距离为 4
第 4 页 共 23 页
v
1
v
3
v
5
有向距离为 2
W
0
W
1
W
2
W
3
W
4
W
5
3
0
8
3
4
5
0
8
10
3
4
5
0
8
10
1
4
0
5
2
2
1
2
0
5
2
2
1
2
0
5
2
2
231
342
150
205
082
272
231
342
150
205
072
272
9
0
1
0
2
6
7
9
0
1
0
2
11
6
16
7
9
0
1
0
2
11
7
6
7
16
0
9
1
0
2
11
7
16
4
6
4
13
0
9
1
0
2
11
7
16
4
6
4
13
723180
834201
615072
720486
507264
027284
7
1
2
7
0
5
2
0
7
1
2
7
0
5
2
0
16
7
1
2
7
0
5
2
0
7
5
0
10
11
12
7
5
0
R
0
R
1
R
004320
050301
050001
650300
604320
054301
004320
051101
051011
650300
604320
051311
024320
051101
051011
650300
604322
051311
2
R
3
R
034320
031101
051011
650333
603323
053313
434320
431101
451011
650333
603323
053313
534350
531101
551051
650555
603323
053353
4
R
5
第 5 页 共 23 页
3.
WMax
j
5 ij
)8,7,8,7,8,8(
中心为 V3 或 V5
5
ijW
j
)23,24,27,21,18,21(
中心为 V2
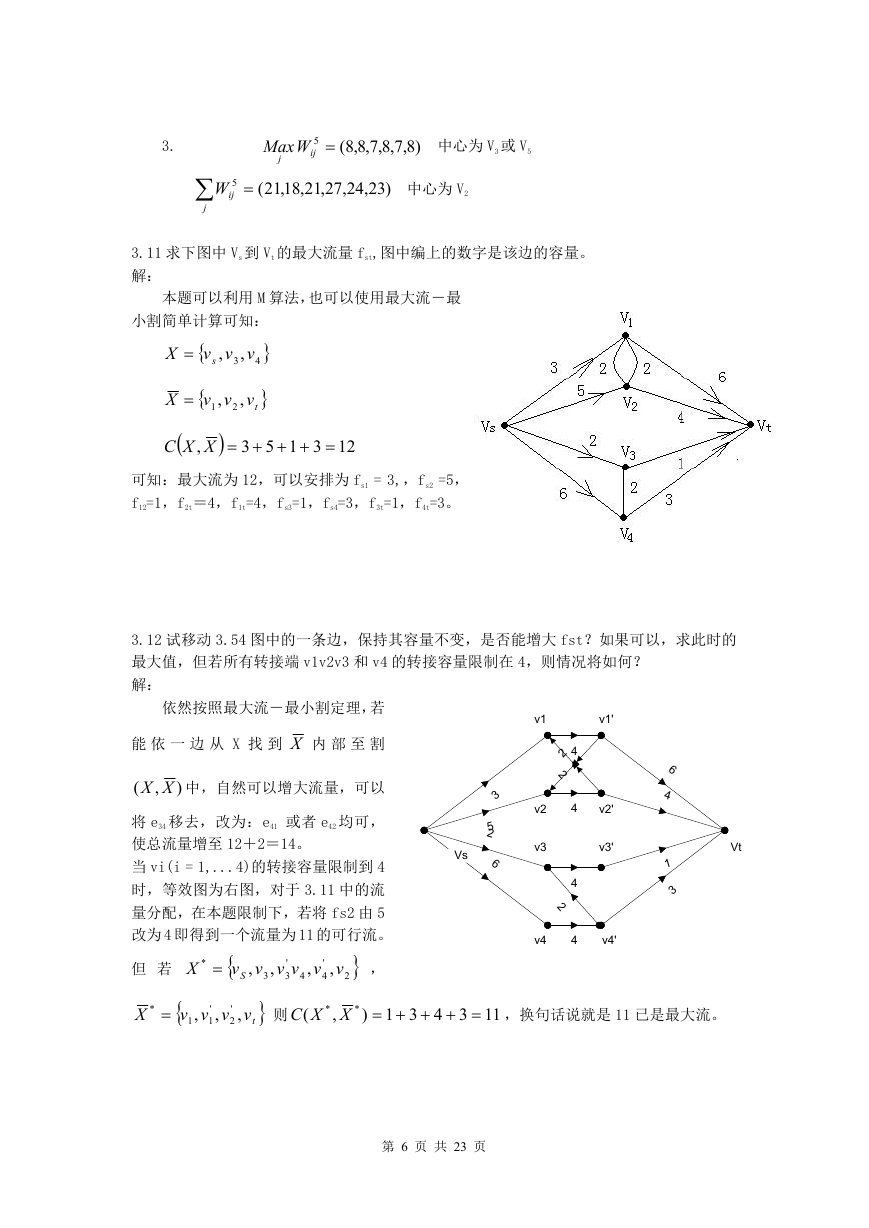
3.11 求下图中 Vs 到 Vt 的最大流量 fst,图中编上的数字是该边的容量。
解：
本题可以利用 M 算法，也可以使用最大流－最
小割简单计算可知：
X
X
3,
vvv
s
,
4
2
,
tvvv
,
1
XXC
3153
,
12
可知：最大流为 12，可以安排为 fs1 = 3,，fs2 =5，
f12=1，f2t＝4，f1t=4，fs3=1，fs4=3，f3t=1，f4t=3。
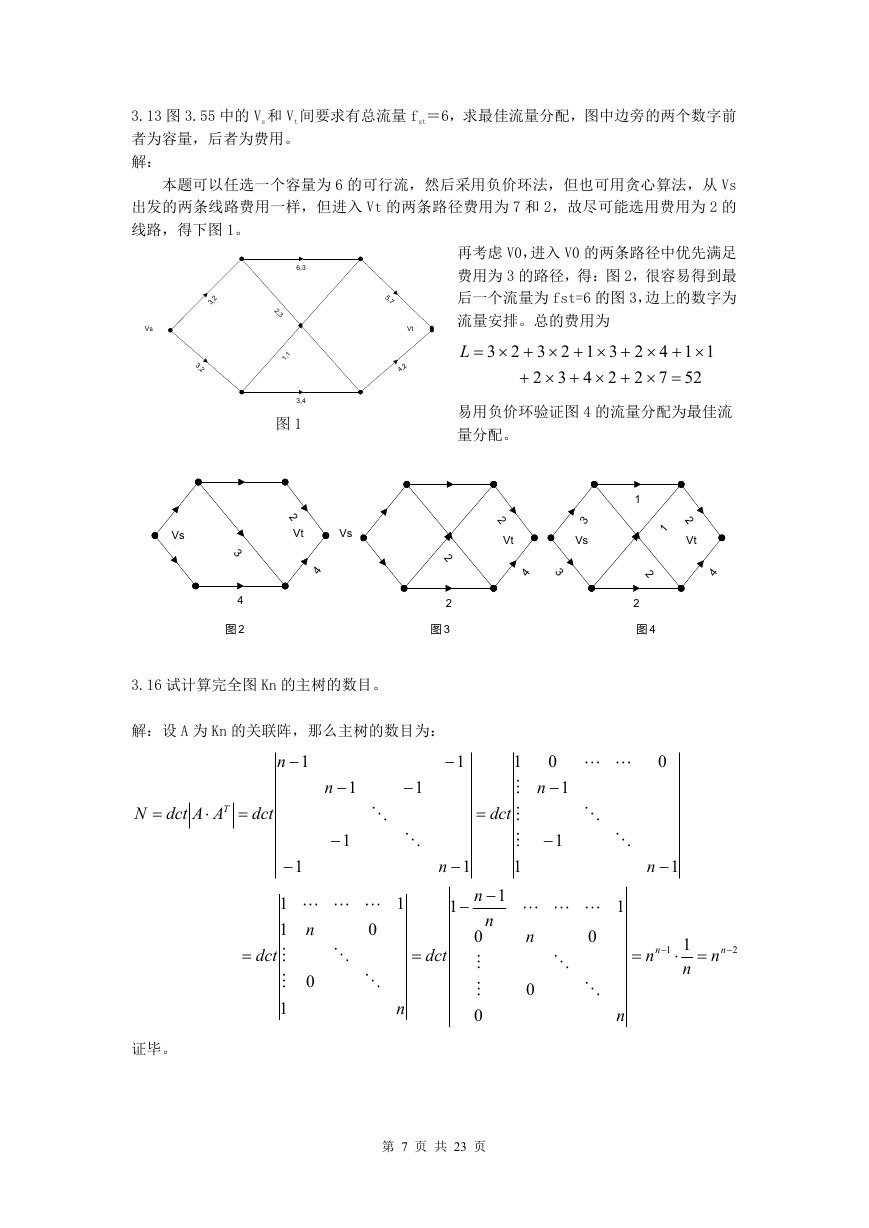
3.12 试移动 3.54 图中的一条边，保持其容量不变，是否能增大 fst？如果可以，求此时的
最大值，但若所有转接端 v1v2v3 和 v4 的转接容量限制在 4，则情况将如何？
解：
依然按照最大流－最小割定理，若
能 依 一 边 从 X 找 到 X 内 部 至 割
(
XX
,
)
中，自然可以增大流量，可以
将 e34 移去，改为：e41 或者 e42 均可，
使总流量增至 12＋2＝14。
当 vi(i = 1,...4)的转接容量限制到 4
时，等效图为右图，对于 3.11 中的流
量分配，在本题限制下，若将 fs2 由 5
改为 4 即得到一个流量为 11 的可行流。
,
vvvvv
3
'
4
'
3
,
,
4
2
，
但 若
X
*
*
v
S
,
X
tvvvv
,
'
2
'
1
,
,
1
3
5
2
6
Vs
v1
v1'
2
4
2
4
4
4
2
v2
v3
v4
v2'
v3'
v4'
6
4
1
3
Vt
则
XXC
(
,
*
*
)
3431
11
，换句话说就是 11 已是最大流。
第 6 页 共 23 页
3.13 图 3.55 中的 Vs 和 Vt 间要求有总流量 fst＝6，求最佳流量分配，图中边旁的两个数字前
者为容量，后者为费用。
解：
本题可以任选一个容量为 6 的可行流，然后采用负价环法，但也可用贪心算法，从 Vs
出发的两条线路费用一样，但进入 Vt 的两条路径费用为 7 和 2，故尽可能选用费用为 2 的
线路，得下图 1。
Vs
3,2
6,3
2,3
3,2
1,1
3,4
图 1
5,7
Vt
4,2
再考虑 V0，进入 V0 的两条路径中优先满足
费用为 3 的路径，得：图 2，很容易得到最
后一个流量为 fst=6 的图 3，边上的数字为
流量安排。总的费用为
11423123
L
2432
52
72
23
易用负价环验证图 4 的流量分配为最佳流
量分配。
3
Vs
4
图 2
2
Vt
Vs
4
2
2
Vt
4
3
2
图 3
3.16 试计算完全图 Kn 的主树的数目。
解：设 A 为 Kn 的关联阵，那么主树的数目为：
1
3
Vs
2
1
2
图 4
2
Vt
4
N
T
AAdct
dct
n
1
1
n
1
1
1
1
n
1
1
0
1
n
1
1
1
0
n
1
0
n
0
1
n
n
n
1 1
n
n
2
n
dct
1
n
n
0
0
dct
0
n
0
1
1
1
1
n
证毕。
dct
第 7 页 共 23 页
4.1 求 M/M/m（n）中，等待时间 w 的概率密度函数。
解：
M/M/m（n）的概率分布为：
(
)
m
!
k
k
p
0
m
1
(
)
m
!
m
1
1
mn
1
p
0
p
k
(
1
m
r
0
)
m
!
k
m
m
!
k
k
p
0
p
0
k
0
0
mk
1
n
km
k
n
假定 n>m，n≥0，现在来计算概率 P{w>x}，既等待时间大于 x 的概率。
{
}
xwP
n
j
0
}
xwPp
j
{
j
{
其中，Pj{w>x}的概率为：
0}
xwP
j
mj
}
{
xwP
j
i
1}
{
xwP
j
0
e
(
xm
xm
!
i
i
)
0
mj
1
jm
1
n
n
jm
可得：
{
}
xwP
mj
n
1
P
j
xm
e
i
)
(
xm
!
i
P
n
mj
m
m
!
m
m
m
!
m
0
n
1
i
1
mn
mj
i
0
P
0
P
0
mj
j
e
i
0
xm
e
(
(
xm
xm
!
i
im
xm
!
1
i
(
)
m
i
P
0
)
m
!
m
i
)
n
n
P
n
(
)
m
x
e
}
xwP则若n
{
1
特别的，新到顾客需等待的概率为：
{
WP
}0
P
0
(
m
)
m
!
m
1
而
f
w
)(
x
m
Pm
0
)
1(!
m
xm
e
[
m
)
m
(
(
x
!
i
i
)
m
m
(
(
)
x
mn
1
mn
)!1
mn
2
i
)
m
mn
0
1
mn
)!1
]
m
n
(
(
第 8 页 共 23 页
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
