5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn 艾里光纤出射场的自愈特性# 邓洪昌，苑立波** （哈尔滨工程大学理学院，哈尔滨 150001） 摘要：本文分析了二维阵列多芯的微结构艾里光纤出射光场的自愈特性。艾里光纤出射光场 在形状、振幅和相位分布上都与艾里光束的两个最边沿边带光束（L 形边带艾里光束）非常 相似，可用艾里光纤出射光场来近似 L 形边带艾里光束。通过观察光束的坡印廷横向分量 发现，艾里光纤出射场不但保留了 L 形边带艾里光束的大部分光学特性，而且还具有其他 独特的自愈能力。 关键词：衍射；艾里光束；自愈；光波导 中图分类号：O436.1；O438.2；TN252 Self-healing properties of output field from Airy fiber DENG Hongchang, YUAN Libo (College of Science, Harbin Engineering University, Harbin 150001) Abstract: We investigate theoretically the self-healing properties of output field from 2D Airy fiber. We show that the output field from 2D Airy fiber is strikingly similar to L-shape Airy beam in the spatial distribution, amplitude and phase profile. The reconstruction of output field from 2D Airy fiber is monitored through the transverse component of the Poynting vector. The output field from 2D Airy fiber has different ability to remain self-healing during propagation corresponding to L-shape Airy beam. Keywords: Diffraction; Airy beam; Self-healing; Optical waveguide 0 引言 非扩散传输的光束被称为无衍射光束，1987 年，Durnin 等首次从理论和实验上分析了 这种光波[1, 2]。其中存在着一种十分特殊的无衍射光束—艾里光束（Airy beam），Berry 和 Balazs[3]在量子力学背景下从理论上推出薛定谔方程具有无衍射的艾里波包解，从而证明了 艾里光束的无衍射特性。但是由于这种光束具有无限能量，因此它只是一个理想化的光束。 为了使艾里光束能在实际中得到应用，Siviloglou 和 Christodoulides 首次以高斯光立方相位 调制的方式从理论和实验上得到了有限能量的艾里光束[4, 5]。这种有限能量的艾里光束同样 具备理想艾里光束的三大特性，即：无衍射、自由加速和自愈特性。基于这些独特的性质， 有限能量的艾里光束具有极大的应用潜力，例如：光学微操纵[6-8]、等离子体导引[9, 10]和真 空电子束加速[11, 12]等。 目前，艾里光纤生成技术主要基于体光学系统[5]，而这种系统存在体积大、成本高和对 准难等缺点，为了克服空间光调制和几何光学器件的限制，我们提出了一种基于二维阵列多 芯的微结构艾里光纤（2D Airy fiber）[13]。利用这种艾里光纤可以在出射纤端形成 L 形边带 近似艾里光束，这种光束同样继承了理想艾里光束的三大特性，本文将对其自愈特性进行细 致的研究。 1 有限能量二维艾里光束及其 L 形边带艾里光束 有限能量的二维艾里光束可以表示为[14]： 基金项目：国家自然科学基金（11274077，61290314）；111 项目（B13015）；中日 S&T 合作项目 （2010DFA-2770） 作者简介：邓洪昌，（1986-），男，博士研究生，主要研究方向：纤维集成光学。 通信联系人：苑立波，（1962-），男，博士生导师，主要研究方向：纤维集成及传感。E-mail: lbyuan@vip.sina.com - 1 - 

中国科技论文在线 ϕ x y z ( , , ) http://www.paper.edu.cn u m ( s m , ξ m ) （1） = ∏ m x y , = 其中， u s ( ξ m m , s ) Ai[ = m ⎡ exp i × ⎣ ( ( − ξ m 3 ( − ξ m 2 / 2) / 12) v − ξ m m a 2 ( − + m + v ia ξ m m s 2 + m m ( a s ]exp[ m m ) / 2 + ξ m − v s m m 2 a ξ m m v ( − / 2) 2 ξ m m − / 2) ] a v ξ m m m ) ⎤ ⎦ （2） 2 0 和 y z ky = / ξ 2 0 表示归一化传输距 Ai( xs ma > 是截断孔径函数， )ms 为艾里函数， x z kx = / ξ y x x / = 和 0 / 0 离， y = mv ys θ = 为无量纲横向坐标， 0x 和 0y 为归一化坐标， mv 与光束的初始入 0 ( [15]。在 ax = ay = 0.11、x0 = y0 = 5 μm、vm = 0、λ0 = 0.98 μm k x y 射角度 mθ 相关： 和 z = 0 μm 的条件下，图 1（a）给出了有限能量艾里光束的光强分布情况。从图中可看出， 光束能量主要集中于两个分别沿着 x、y 轴方向分布的边带上，由此可以用其对应的 L 形边 带艾里光束（图 1（b））来近似理想的有限能量艾里光束。 ) / , m 0 0 (b) 图 1 艾里光纤光强分布图：（a）二维有限能量二维艾里光束；（b）L 形边带艾里光束 Fig. 1 (color online) Intensity profile of Airy beam. (a) Two-dimensional finite energy Airy beam. (b) L-shaped sideband Airy beam 在傍轴条件下，艾里光束 ( , ϕ 的坡印廷矢量可以表示为[16]： r S = r S z + r S ⊥ x y z , ) 1 2 η 0 = 2 ϕ ˆ z + i k 4 η 0 ∗ ∇ ⎡ ⎤ ϕ ϕ ϕ ϕ ⎦ ⎣ − ∇ ⊥ ⊥ ∗ （3） 其中， 0 η μ ε 0 = 0 / 为真空阻抗， ˆz 表示在 z 轴方向的单位矢量， zSr r 和 S⊥ 分别表示坡 印廷纵向和横向分量。由于坡印廷矢量指出了能量流的方向和大小，因此可以通过检测艾里 r 光束的坡印廷横向分量 S⊥ 2 艾里光纤及其出射光场 来观察其重组自愈合现象[14]。 为了得到 L 形边带艾里光束（如图 2（a）），我们设计了如图 2（b）所示的二维阵列 多芯微结构艾里光纤。从图中可以看出，该光纤纤芯由两组相互垂直的纤芯阵列组成，每组 纤芯的空间排布都满足或近似满足艾里函数（如图 2（c））。当向中央纤芯输入高斯光束 （GB）后，光波会在纤芯阵列中不断耦合，经过一定长度之后，就会实现近似立方相位调 制，在此处截断光纤就可以得到 L 形边带近似艾里输出光束，如图 3（a）所示。 - 2 - 45 50 55 60 65 

中国科技论文在线 (b) Y GB X http://www.paper.edu.cn 2D Airy fiber Z   . 70 75 80 85 90 95 图 2 艾里光纤示意图：（a）L 形边带艾里光束；（b）二维艾里光纤；（c）艾里光纤纤芯阵列的空间排布 Fig. 2 The schematic diagram of 2D Airy fiber. (a) Amplitude profile of L-shaped sideband beam. (b) 2D Airy fiber based on two orthogonal arrayed 5-core. (c) The spatial arrangement of arrayed cores in cross section L 形边带艾里光束作为一种近似的艾里光束同样具备理想艾里光束的大部分光学特性。 从图 3（b）和（c）可以看出，艾里光纤的出射光场的光强和振幅在 X 轴向上的分布与理想 有限能量艾里光束非常相似。这样，艾里光纤出射光场在形状、振幅和相位分布上都十分近 似于 L 型边带艾里光束，因此可以推断出艾里光纤出射光场也同样继承或部分继承了艾里 光束的无衍射、自由加速和自愈特性。 (a) (b) 图 3 艾里光纤的出射光场：（a）横截面光场振幅分布图；（b）X 轴向上的振幅和相位分布图； （c）对应理想二维有限能量艾里光束传输到 70mm 处的振幅和相位分布 Fig. 3. Output field from 2D Airy fiber. (a) Amplitude profile of output Airy-like beam. (b), (c) Amplitude (red line) and phase curve (blue line) of Airy-like beam and corresponding two-dimensional finite energy Airy beam after propagating 70 μm, respectively. 3 艾里光纤出射光场的自愈合现象 同贝塞尔光束一样，艾里光束也具有自愈特性[14]。当艾里光束在传输过程中丢失部分 信息后，光束可以通过内部能量的流动来实现重组进而完成自愈。为了分析艾里光纤出射光 r 场的自愈特性，我们采用公式（3）中的坡印廷横向分量 S⊥ 流动情况。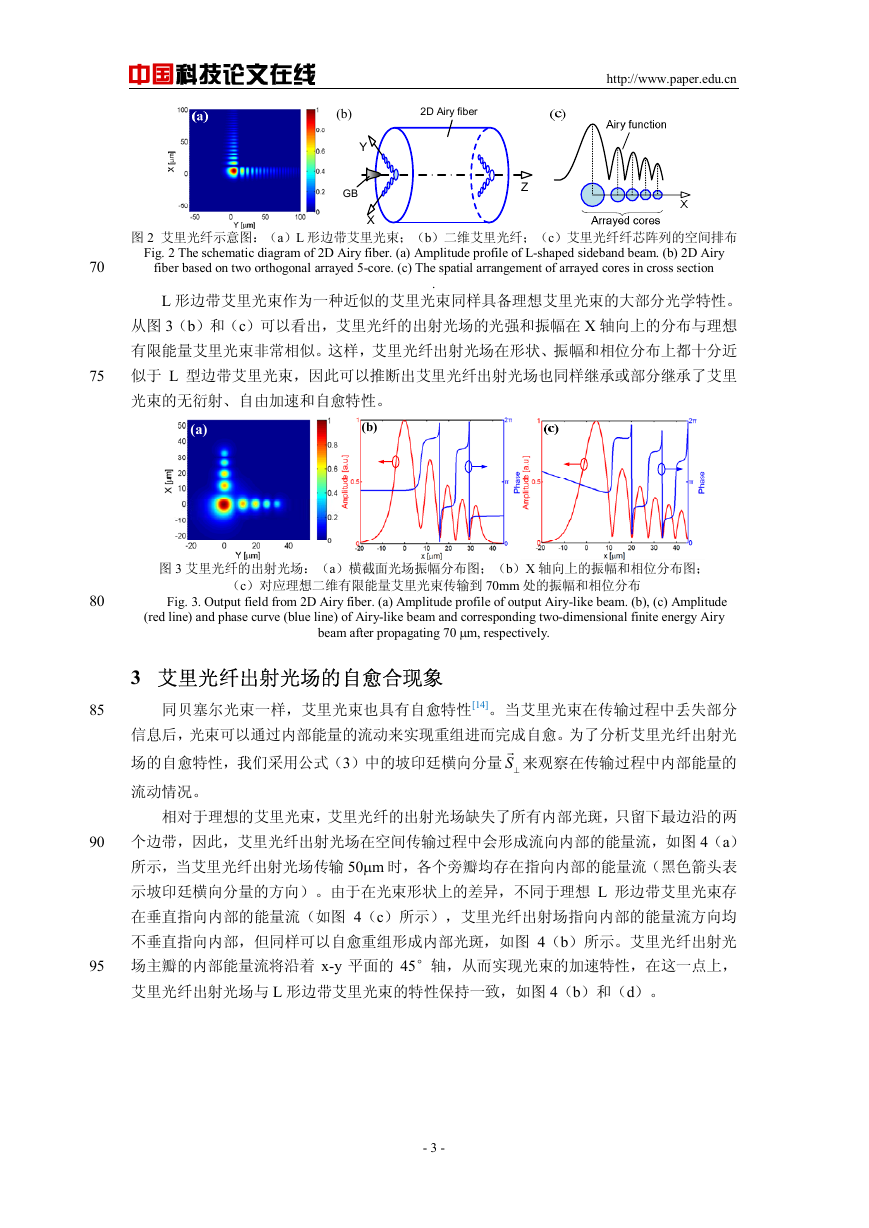 来观察在传输过程中内部能量的 相对于理想的艾里光束，艾里光纤的出射光场缺失了所有内部光斑，只留下最边沿的两 个边带，因此，艾里光纤出射光场在空间传输过程中会形成流向内部的能量流，如图 4（a） 所示，当艾里光纤出射光场传输 50μm 时，各个旁瓣均存在指向内部的能量流（黑色箭头表 示坡印廷横向分量的方向）。由于在光束形状上的差异，不同于理想 L 形边带艾里光束存 在垂直指向内部的能量流（如图 4（c）所示），艾里光纤出射场指向内部的能量流方向均 不垂直指向内部，但同样可以自愈重组形成内部光斑，如图 4（b）所示。艾里光纤出射光 场主瓣的内部能量流将沿着 x-y 平面的 45°轴，从而实现光束的加速特性，在这一点上， 艾里光纤出射光场与 L 形边带艾里光束的特性保持一致，如图 4（b）和（d）。 - 3 - 

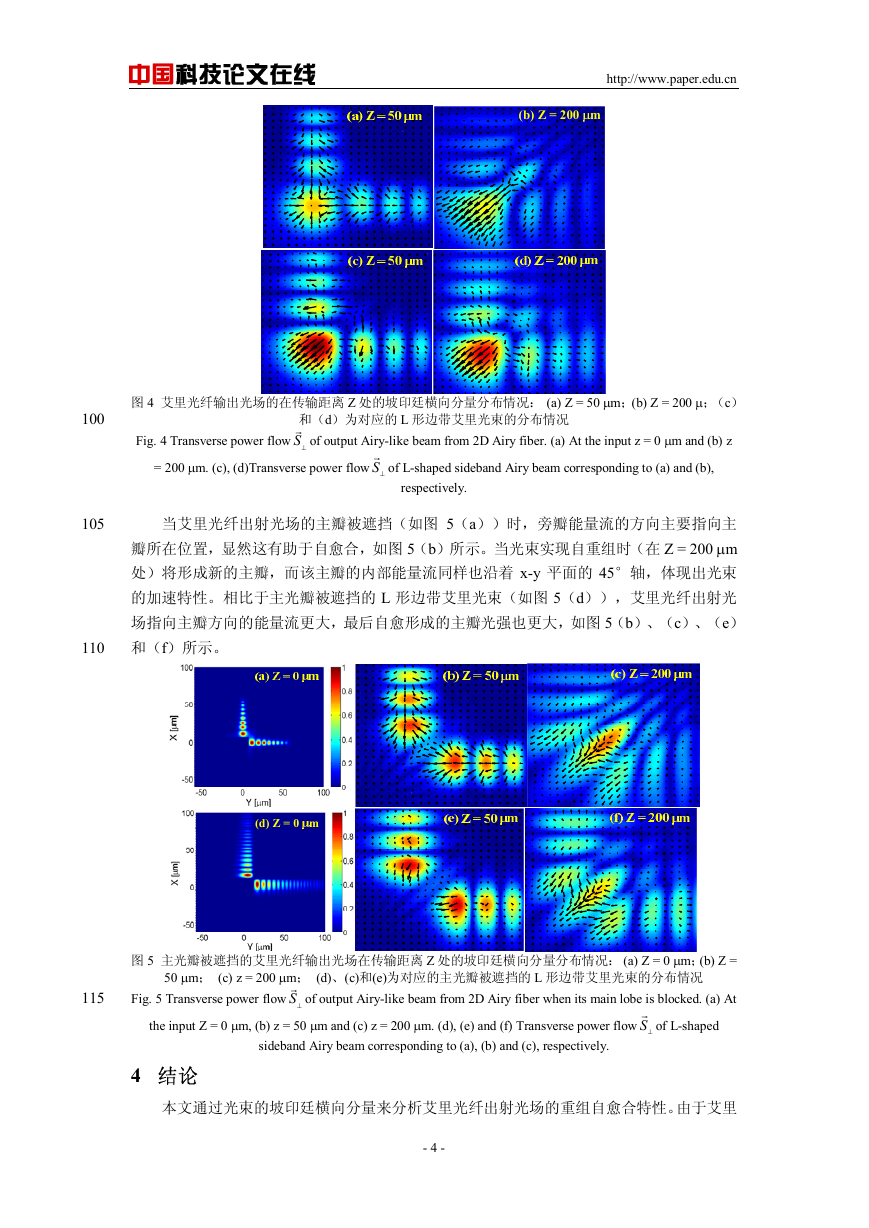
中国科技论文在线 http://www.paper.edu.cn (b) Z = 200 m 100 105 110 115 图 4 艾里光纤输出光场的在传输距离 Z 处的坡印廷横向分量分布情况： (a) Z = 50 μm；(b) Z = 200 μ；（c） Fig. 4 Transverse power flow S⊥ 和（d）为对应的 L 形边带艾里光束的分布情况 r of output Airy-like beam from 2D Airy fiber. (a) At the input z = 0 μm and (b) z = 200 μm. (c), (d)Transverse power flow S⊥ r of L-shaped sideband Airy beam corresponding to (a) and (b), respectively. 当艾里光纤出射光场的主瓣被遮挡（如图 5（a））时，旁瓣能量流的方向主要指向主 瓣所在位置，显然这有助于自愈合，如图 5（b）所示。当光束实现自重组时（在 Z = 200 μm 处）将形成新的主瓣，而该主瓣的内部能量流同样也沿着 x-y 平面的 45°轴，体现出光束 的加速特性。相比于主光瓣被遮挡的 L 形边带艾里光束（如图 5（d）），艾里光纤出射光 场指向主瓣方向的能量流更大，最后自愈形成的主瓣光强也更大，如图 5（b）、（c）、（e） 和（f）所示。 (d) Z = 0 m (b) 图 5 主光瓣被遮挡的艾里光纤输出光场在传输距离 Z 处的坡印廷横向分量分布情况： (a) Z = 0 μm；(b) Z = 50 μm； (c) z = 200 μm； (d)、(c)和(e)为对应的主光瓣被遮挡的 L 形边带艾里光束的分布情况 Fig. 5 Transverse power flow S⊥ r of output Airy-like beam from 2D Airy fiber when its main lobe is blocked. (a) At the input Z = 0 μm, (b) z = 50 μm and (c) z = 200 μm. (d), (e) and (f) Transverse power flow S⊥ r of L-shaped sideband Airy beam corresponding to (a), (b) and (c), respectively. 4 结论 本文通过光束的坡印廷横向分量来分析艾里光纤出射光场的重组自愈合特性。由于艾里 - 4 - 

120 125 130 135 140 145 150 155 160 中国科技论文在线 http://www.paper.edu.cn 光纤出射光场的形状、振幅和相位分布都与理想二维有限能量艾里光束的两个最边沿边带 （L 形边带）非常相似，因此我们用艾里光纤出射光场来近似 L 形边带艾里光束。通过分析 艾里光纤出射光场的坡印廷横向分量发现，在传输过程中，艾里光纤出射光场和 L 形边带 艾里光束的自愈特性存在许多相同点和不同点。它们都存在指向光束内部的能量流，但由于 在光束形状上的差异，不同于理想 L 形边带艾里光束存在垂直指向内部的能量流，艾里光 纤出射场指向内部的能量流方向均不垂直指向内部，但它们都会自愈重组形成内部光斑，并 且主瓣的内部能量流都沿着 x-y 平面的 45°轴，体现出光束的加速特性。当艾里光纤出射 光场和 L 形边带艾里光束的主瓣被遮挡时，它们都会实现自重组形成新的主瓣，并且该主 瓣的内部能量流都沿着 x-y 平面的 45°轴，但不同之处在于，艾里光纤出射光场指向主瓣 方向的能量流更大，最终自愈形成的主瓣光强也更大。总之，艾里光纤出射场不但保留了 L 形边带艾里光束的大部分光学特性，而且还具有其他独特的自愈能力。 [参考文献] (References) [1] J. Durnin. Exact solutions for nondiffracting beams. I. The scalar theory[J]. J. Opt. Soc. Am. A，1987，4 (4)： 651-654 [2] J. Durnin, J. Miceli Jr, J. Eberly. Diffraction-free beams[J]. Physical Review Letters，1987，58 (15)：1499-1501 [3] M. V. Berry,N. Balazs. Nonspreading wave packets[J]. Am. J. Phys，1979，47 (3)：264-267 [4] G. A. Siviloglou,D. N. Christodoulides. Accelerating finite energy Airy beams[J]. Optics Letters，2007，32 (8)： 979-981 [5] G. Siviloglou, J. Broky, A. Dogariu et al.. Observation of accelerating Airy beams[J]. Physical Review Letters， 2007，99 (21)：213901 [6] J. Baumgartl, M. Mazilu, K. Dholakia. Optically mediated particle clearing using Airy wavepackets[J]. Nature photonics，2008，2 (11)：675-678 [7] P. Zhang, J. Prakash, Z. Zhang et al.. Trapping and guiding microparticles with morphing autofocusing Airy beams[J]. Optics letters，2011，36 (15)：2883-2885 [8] Z. Zheng, B. F. Zhang, H. Chen et al.. Optical trapping with focused Airy beams[J]. Applied Optics，2011，50 (1)：43-49 [9] P. Polynkin, M. Kolesik, J. Moloney. Filamentation of femtosecond laser Airy beams in water[J]. Physical review letters，2009，103 (12)：123902 [10] P. Polynkin, M. Kolesik, J. V. Moloney et al.. Curved plasma channel generation using ultraintense Airy beams[J]. Science，2009，324 (5924)：229 [11] J. X. Li, W. P. Zang, J. G. Tian. Vacuum laser-driven acceleration by Airy beams[J]. Optics express，2010， 18 (7)：7300-7306 [12] J. X. Li, X. L. Fan, W. P. Zang et al.. Vacuum electron acceleration driven by two crossed Airy beams[J]. Optics Letters，2011，36 (5)：648-650 [13] H. Deng,L. Yuan， Design of a novel quasi-Airy beam generator: Airy optical fiber[C]，OFS2012 22nd International Conference on Optical Fiber Sensor, (International Society for Optics and Photonics, 2012), 84218Y-84218Y-84214 [14] J. Broky, G. A. Siviloglou, A. Dogariu et al.. Self-healing properties of optical Airy beams[J]. Optics Express，2008，16 (17)：12880-12891 [15] G. Siviloglou, J. Broky, A. Dogariu et al.. Ballistic dynamics of Airy beams[J]. Optics Letters，2008，33 (3)： 207-209 [16] L. Allen, M. Beijersbergen, R. Spreeuw et al.. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A，1992，45 (11)：8185-8189 - 5 -