logo资料库

基于忆阻器的时滞混沌系统和伪随机序列发生器.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：2.73M 资料格式：pdf 举报 版权申诉
第1页 / 共12页
第2页 / 共12页
第3页 / 共12页
第4页 / 共12页
第5页 / 共12页
第6页 / 共12页
第7页 / 共12页
第8页 / 共12页
资料共12页，剩余部分请下载后查看
    1引 言
    2一个新的时滞混沌系统模型
    Fig 1
    3平衡点分析
    3.1 = 0时平衡点的稳定性
    3.2 =0时平衡点的稳定性
    Fig 2
    4数值仿真
    4.1 系统随参数a的变化
    Fig 3
    4.2 系统随参数b的变化
    Fig 4
    4.3 系统随时延的变化
    Fig 5
    Fig 6
    Fig 7
    Fig 8
    5混沌伪随机序列的特性
    5.1 混沌伪序列相关性分析
    Fig 9
    5.2 时滞混沌系统复杂度分析
    Table 1
    6结 论
    References
    Abstract
    基于忆阻器的时滞混沌系统及伪随机序列发生器 吴洁宁 王丽丹 段书凯 A memristor-based time-delay chaotic systems and pseudo-random sequence generator Wu Jie-Ning Wang Li-Dan Duan Shu-Kai 引用信息 Citation: Acta Physica Sinica, 66, 030502 (2017) DOI: 10.7498/aps.66.030502 在线阅读 View online: http://dx.doi.org/10.7498/aps.66.030502 当期内容 View table of contents: http://wulixb.iphy.ac.cn/CN/Y2017/V66/I3 您可能感兴趣的其他文章 Articles you may be interested in 磁控二氧化钛忆阻混沌系统及现场可编程逻辑门阵列硬件实现 A memristor-based chaotic system and its field programmable gate array implementation 物理学报.2016, 65(12): 120503 http://dx.doi.org/10.7498/aps.65.120503 二维 H 閚 on-Heiles 势及其变形势体系逃逸率与分形维数的研究 Fractal dimensions and escape rates in the two-dimensional H 閚 on-Heiles potential and its deformation form 物理学报.2015, 64(23): 230501 http://dx.doi.org/10.7498/aps.64.230501 离子迁移忆阻混沌电路及其在语音保密通信中的应用 Chaotic circuit of ion migration memristor and its application in the voice secure communication 物理学报.2015, 64(21): 210507 http://dx.doi.org/10.7498/aps.64.210507 一种参数优化的混沌信号自适应去噪算法 A parameter optimization nonlinear adaptive denoising algorithm for chaotic signals 物理学报.2015, 64(4): 040503 http://dx.doi.org/10.7498/aps.64.040503 蔡氏电路的功能全同电路与拓扑等效电路及其设计方法 Equivalent circuit in function and topology to Chua's circuit and the design methods of these circuits 物理学报.2014, 63(20): 200503 http://dx.doi.org/10.7498/aps.63.200503
    物 理 学 报 Acta Phys. Sin. Vol. 66, No. 3 (2017) 030502 基于忆阻器的时滞混沌系统及伪随机序列发生器 吴洁宁1)2) 王丽丹1)2)y 段书凯1)2) 1)(西南大学电子信息工程学院, 重庆 400715) 2)(非线性电路与智能信息处理重庆市重点实验室, 重庆 400715) ( 2016 年 6 月 21 日收到; 2016 年 10 月 7 日收到修改稿 ) 忆阻器作为可调控的非线性元件, 很容易实现混沌信号的产生. 基于忆阻器的混沌系统是当下研究的热 点, 但是基于忆阻器的时滞混沌系统目前却鲜有人涉足. 因此, 本文提出了一个新型忆阻时滞混沌系统. 时延 的存在增加了系统的复杂性, 使系统能够产生更丰富、更复杂的动力学行为. 我们对提出的忆阻时滞混沌系统 进行了稳定性分析, 确定了显示系统稳定平衡点的相应参数区域. 讨论了在不同参数情况下的系统状态, 系 统呈现出形态各异的混沌吸引子相图, 表现出丰富的混沌特性和非线性特性. 最后, 将系统用于产生伪随机 序列, 并经过实验验证, 我们提出的系统具有良好的自相关性和互相关性, 同时能获得相对显著的近似熵. 该 时滞混沌系统具有复杂的动力学行为和良好的随机性, 能满足扩频通信和图像加密等众多领域的应用需要. 关键词: 忆阻器, 时滞混沌, 稳定性分析, 随机性分析 PACS: 05.45.Ac, 05.45.Pq, 05.45.Tp, 02.30.Ks DOI: 10.7498/aps.66.030502 1 引 言 忆阻器是 Chua [1] 于 1971 年提出的一种具有 记忆功能的非线性电阻, 2008 年惠普 (HP) 实验室 Strukov 等 [2] 数学推导出了 HP 忆阻器模型, 并且 物理实现了忆阻器, 制造出了世界上第一个忆阻 器. 此后, 忆阻器日益受到学术界的重视, 在非线 性科学领域、神经网络领域、材料科学领域都得到 广泛的关注和研究 [36]. 忆阻器作为可调控的纳米 级器件, 在非线性领域有着巨大的应用前景, 可以 开拓性地推进这类传统领域的发展. 由于忆阻器的 电荷和磁通具有奇对称的特性 [7;8], Itoh 和 Chua [9] 运用一个磁通控制的分段线性忆阻器模型替换了 蔡氏混沌电路中的蔡氏二极管, 实现了第一个基于 忆阻器的混沌系统. Muthuswamy 和 Kokate [10] 采 用运算放大器和乘法器等基本电子元件实现了一 个忆阻器等效电路, 并用光滑忆阻器模型代替蔡氏 混沌电路中的蔡氏二极管, 实现了一些新的忆阻混 沌电路. 在这些开创性研究的推动下, 越来越多的 探索致力于各类忆阻混沌系统的研究 [1114]. 近年 的研究中, 基于忆阻器的多涡卷混沌系统、分数阶 混沌系统、超混沌系统都呈现出了丰富的动力学特 性 [1517], 但是目前鲜有人提出基于忆阻器的时滞 混沌系统. 自从提出描述生理控制系统的 Mackey-Glass 方程以来 [18], 越来越多的研究致力于探索时滞动 力系统的动力学行为. 时延的存在增加了系统的 复杂性, 使系统能够产生更丰富、更复杂的动力学 行为. 许多自然系统可以用非线性时滞微分方程 (DDE) 进行数学建模 [19], 比如白血病人的产血机 制的 Mackey-Glass 模型、光学双稳态谐振器动力学 的 Ikeda 系统、厄尔尼诺和南方涛动 (ENSO)、神经 网络、种群动态、肿瘤生长、基因调控网络、控制系 统等 [2024]. 引入延迟的非线性系统中最主要的复 杂性是相空间中有限维到无限维的变化, 可能导致 国家自然科学基金 (批准号: 61372139, 61672436, 61571372)、新世纪优秀人才支持计划 (批准号: 教技函 [2013]47 号) 和中央高 校基本科研业务费专项资金 (批准号: XDJK2016A001, XDJK2014A009) 资助的课题. † 通信作者. E-mail: ldwang@swu.edu.cn © 2017 中国物理学会 Chinese Physical Society 030502-1 http://wulixb.iphy.ac.cn
    物 理 学 报 Acta Phys. Sin. Vol. 66, No. 3 (2017) 030502 8>>><>>>:ROFF; RON; M (0) + kx(t); x(t) < c1; c1 6 x(t) < c2; x(t) > c2; M (t) = 其中, 系统的不稳定性以及许多复杂的现象, 比如混沌、 超混沌、多稳定性、分岔、振荡消失等. 混沌系统可 以应用到保密通信系统、基于混沌的噪声发生器、 传感器的改善以及机器人的运动功能中. 由于这 些原因, 我们旨在设计能产生混沌现象的简单的时 滞系统 [25]. 因此, 寻找一个封闭形式的数学函数作 为非线性部分的时滞动力系统值得特别关注. 此 外, 时滞混沌系统稳定性的分析和控制设计也是目 前研究的热点, 因为它们恰当地描述了真实的物理 情况. 本文在经典 Mackey-Glass 系统的基础上, 利 用忆阻器的忆阻值和电荷之间的非线性函数关系, 提出了一种新的非线性时滞混沌系统. 我们对所提 出的忆阻时滞混沌系统进行了稳定性分析, 确定了 系统相应的稳定平衡点的参数区域, 讨论了系统在 不同参数情况下的稳定性. 发现了系统在不同参数 情况下呈现出多样的混沌吸引子相图, 具有丰富的 混沌特性和非线性特性. 新的时滞混沌系统所产生 的伪随机序列具有良好的自相关性和互相关性, 同 时能获得相对显著的复杂度, 表明本文所提出的新 的时滞混沌系统具有复杂的动力学行为和良好的 随机性, 可以作为新型的扩频序列应用于信息安全 领域中. 本文下面的内容安排如下: 第 2 部分介绍 了本文提出的忆阻时滞混沌系统的数学模型; 第 3 部分计算了系统的平衡点并对每个平衡点进行了 稳定性分析, 确定了系统的参数范围; 第 4 部分发 现了系统在不同参数情况下具有丰富的非线性运 动轨迹, 对其进行了数值仿真, 并验证了系统在不 同参数情况下的系统状态; 第 5 部分通过对提出的 系统所产生的伪随机序列的相关性和复杂度的计 算和仿真, 对忆阻时滞混沌系统的随机性和复杂 性进行了研究和分析; 第 6 部分对整个工作进行了 总结. 2 一个新的时滞混沌系统模型 本文提出一个基于忆阻器的时滞混沌系统, 其 方程如下: _x = ax + bM (x(t )); (1) 这里 a, b 是系统参数; 是延迟时间; x(t) 是忆阻器 的电荷; M () 表示忆阻值与电荷 x 之间的函数 [14], (2) (3) (4) (5) ROFF M (0) RON M (0) k ; ; k c1 = c2 = k 是一个常数, k = (RON ROFF)VRON D2 ; D 是 忆 阻 薄 膜 器 件 的 厚 度, M (0) 是 忆 阻 器 的 初 始值, RON 和 ROFF 分别代表当 TiO2x 层的厚度 为 D 和 0 时的极限忆阻值, V 是氧空穴的平均迁 移 率. 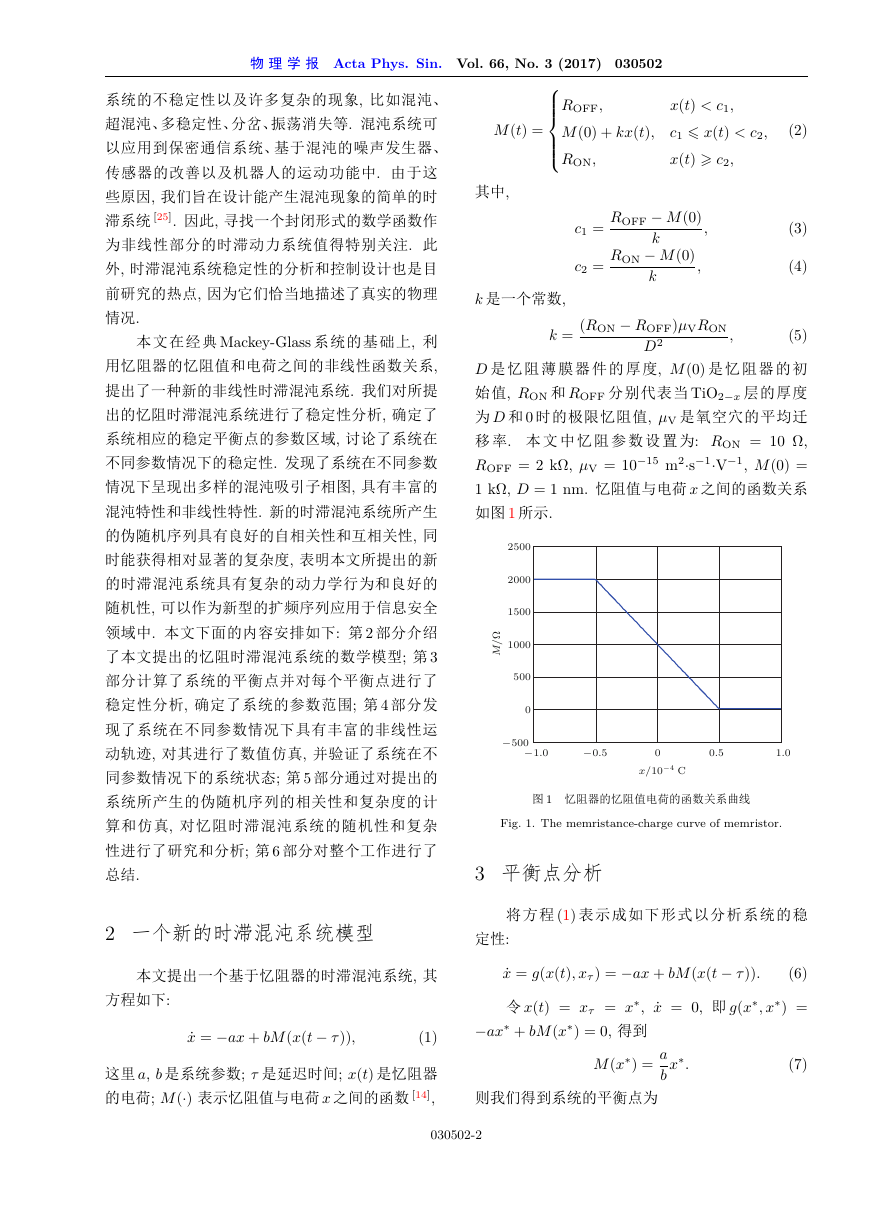本 文 中 忆 阻 参 数 设 置 为: RON = 10 Ω, 15 m2s1V1, M (0) = ROFF = 2 kΩ, V = 10 1 kΩ, D = 1 nm. 忆阻值与电荷 x 之间的函数关系 如图 1 所示. 图 1 忆阻器的忆阻值电荷的函数关系曲线 Fig. 1. The memristance-charge curve of memristor. 3 平衡点分析 将方程 (1) 表示成如下形式以分析系统的稳 定性: _x = g(x(t); x ) = ax + bM (x(t )): _x = 0, 即 g(x , 令 x(t) = x = x ) = 0, 得到 + bM (x ; x ax ) = M (x : x a b 则我们得到系统的平衡点为 (6) ) = (7) 030502-2 -1.0-0.500.51.0-50005001000150020002500x⊳-4 CM/W
    物 理 学 报 Acta Phys. Sin. Vol. 66, No. 3 (2017) 030502 ROFF; x < c1; 8>>>>>><>>>>>>: 0 = x 0 = x 0 = x b a bM (0) a bk b a RON; ; < c2; (8) c1 6 x > c2: x 从 (6) 式, 我 们 可 以 分 别 得 到 关 于 x 和 x 的 1) 同样地, 由 (8)—(11) 式可知, 当 x < c1 和 > c2 时, > 0 时系统的平衡点和特征方程与 x 3.1 节讨论的 = 0 时的平衡点和特征方程相同, 即在任意的参数 a > 0 的情况下, x ROFF 和 0 = RON都是稳定的平衡点. 0 = b a x < c2 时, 由 (8) 式, 系统的平衡点 , 此时系统的特征方程为一个指数 b a 2) 当 c1 6 x bM (0) a bk 0 = (16) (17) (18) (19) a + bk e = 0: (15) 设 = + iv, 其中 和 v 为实数. 平衡点的渐 近稳定性发生在特征方程所有的根都存在负实部 时. 如果 的值从虚部变到实部, 则 < 0 代表稳 定状态, > 0 代表分岔状态, = 0 代表极限情况, 即当 = 0 时平衡点的稳定性会发生改变, 出现临 界稳定曲线. 下面我们假设 = 0, 将 = iv 代入 特征方程 (11): J0 + J eiv iv = 0; J0 + J [cos(v ) i sin(v )] iv = 0: 由 (17) 式的实部和虚部我们可以分别得到 J cos(v ) = J0; J sin(v ) = v: √ ( 联立 (18) 和 (19) 式可以得到 ) v = J 2 0 : J 2 (20) 当且仅当jJj > jJ0j 时成立, 即jbkj > a(这里我们 设 a > 0), jbj > a (由忆阻参数知 k 的值为负). 由 k (18) 式可得到 J0 J v = arccos + 2n; (21) 这里 n = 0;1;2; , 当且仅当 J ̸= 0, 即 bk ̸= 0 时成立. 因此对于jJj > jJ0j 及确定的 v(当 v > 0 d 时), 在 (; a; b) 参数空间中, 对于任一曲线如果 d d d′ 的值为正, 则可以判 的值是负的, 而其他曲线 定稳定域存在于 的值为负的两条曲线之间: )] )] d d 2n + arccos [ [ 2n arccos ( ( k2b2 a2 k2b2 a2 p p a bk a bk 1(n) = 2(n) = ; ; (22) (23) (9) 为 x 方程: 8>>><>>>:0; 0; bk; x < c1; c1 6 x > c2: x < c2; (10) Jacobian 矩阵, 即 @g(x; x ) = a; J0 = Jjx =x @x = @g(x; x ) @x = 系统的特征方程为 J0 + J e = 0: (11) 3.1 = 0 时平衡点的稳定性 当 = 0 时, 由特征方程 (11) 式可以得到 1) 当 x = J0 + J : < c1 时, 系 统 的 平 衡 点 为 x (12) 0 = > c2 时, 系统的平衡 RON, 特征根 = a. 所以, 在任意的 ROFF, 特征根 = a; 当 x b a 点为 x 0 = b a 0 = b a ROFF 和 x 0 = b a RON 参数 a > 0 的情况下, x 都是稳定的平衡点. 2) 当 c1 6 x < c2 时, 系 统 的 平 衡 点 为 0 = bM (0)/(a bk), 特征根 = a + bk. 当 x 特征根 存在负实部时, 平衡点是稳定的. 固当 0 = bM (0)/(a bk) 为稳定的平衡点. a > bk 时, x 由 (5) 式及相应的忆阻参数可知 k 的值为负数, 固综上 (1) 和 (2) 式我们得到当 = 0 时平衡点稳定 的条件为 a > 0; b > a/k: (13) (14) 所以当 = 0, 且参数 a, b 满足以上条件时, 系统的 平衡点为渐近稳定的. (13) 和 (14) 式为选择系统参 数的第一个条件. 3.2 ̸= 0 时平衡点的稳定性 在系统存在时延 的情况下, 对系统平衡点的 稳定性讨论如下. 030502-3
    物 理 学 报 Acta Phys. Sin. Vol. 66, No. 3 (2017) 030502 d > 0, 而在 的负值到正值的范围内, 其他曲线 d 2(n) < < 1(n)(n > 0) 都不满足所需的平衡条 件, 因此它们都属于非稳定域. (22) 式中 n = 0; 1; 2; , (23) 式中 n = 1; 2; , n 选取不同的值是为了分别满足两式中的 为正. 同 样地, 当 v < 0 时, 存在一组与 (22) 和 (23) 式相同 的方程, 此时 n 的取值为负数, 以保证 的值为正. 在 > 0 的条件下, 为了确定曲线 1(n), 2(n) 包 含的稳定域, 需要分析这些曲线对应的 或者 d d 的特性, 当导数的值为负时即为所求的 Re 临界曲线. 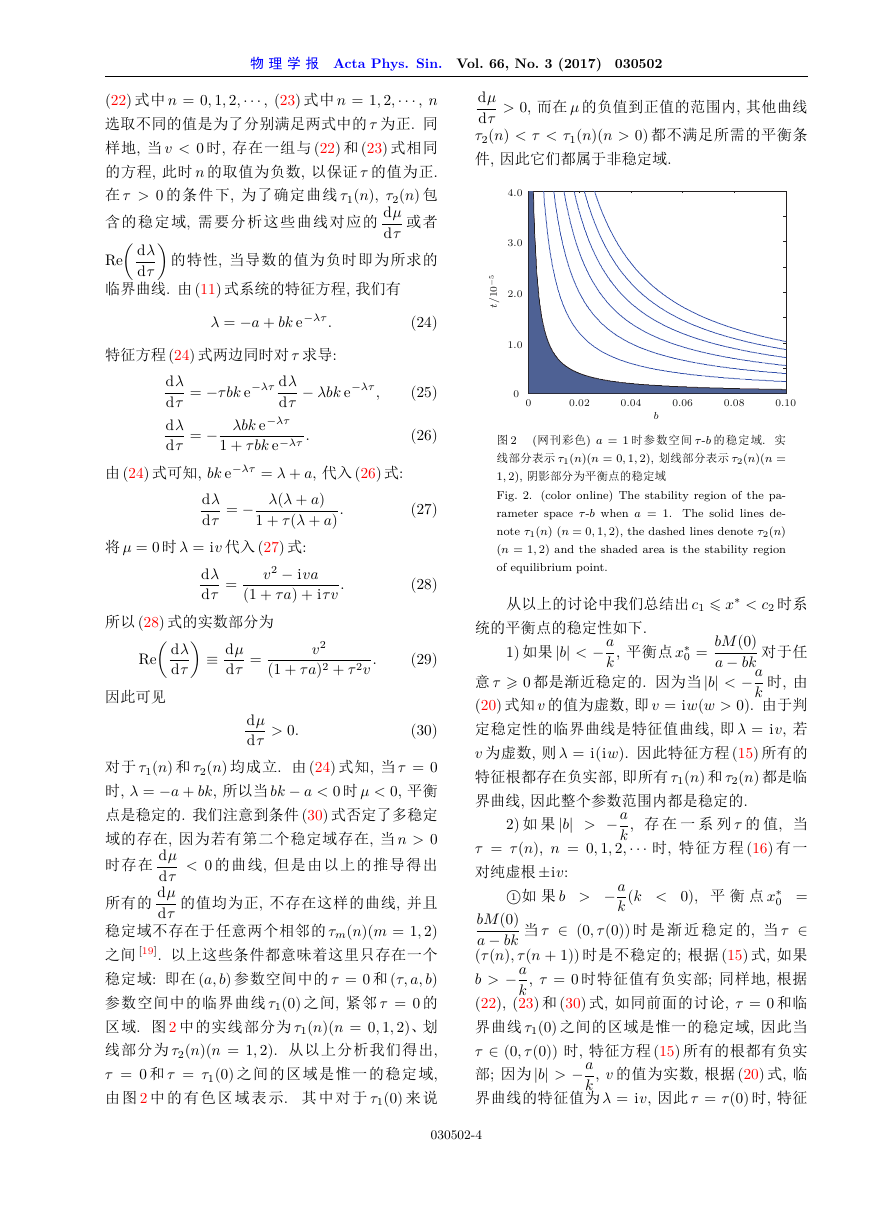由 (11) 式系统的特征方程, 我们有 ( ) d d = a + bk e : 特征方程 (24) 式两边同时对 求导: d d d d bk e ; = bk e d d = bk e 1 + bk e : 由 (24) 式可知, bk e = + a, 代入 (26) 式: d d = ( + a) 1 + ( + a) : 将 = 0 时 = iv 代入 (27) 式: v2 iva d d = (1 + a) + i v : 所以 (28) 式的实数部分为 ( ) d d Re 因此可见 (24) (25) (26) (27) (28) 图 2 (网刊彩色) a = 1 时参数空间 -b 的稳定域. 实 线部分表示 1(n)(n = 0; 1; 2), 划线部分表示 2(n)(n = 1; 2), 阴影部分为平衡点的稳定域 Fig. 2. (color online) The stability region of the pa- rameter space -b when a = 1. The solid lines de- note 1(n) (n = 0; 1; 2), the dashed lines denote 2(n) (n = 1; 2) and the shaded area is the stability region of equilibrium point. 从以上的讨论中我们总结出 c1 6 x < c2 时系 d d = v2 (1 + a)2 + 2v : (29) d d > 0: (30) d d d d 对于 1(n) 和 2(n) 均成立. 由 (24) 式知, 当 = 0 时, = a + bk, 所以当 bk a < 0 时 < 0, 平衡 点是稳定的. 我们注意到条件 (30) 式否定了多稳定 域的存在, 因为若有第二个稳定域存在, 当 n > 0 < 0 的曲线, 但是由以上的推导得出 时存在 的值均为正, 不存在这样的曲线, 并且 所有的 稳定域不存在于任意两个相邻的 m(n)(m = 1; 2) 之间 [19]. 以上这些条件都意味着这里只存在一个 稳定域: 即在 (a; b) 参数空间中的 = 0 和 (; a; b) 参数空间中的临界曲线 1(0) 之间, 紧邻 = 0 的 区域. 图 2 中的实线部分为 1(n)(n = 0; 1; 2)、划 线部分为 2(n)(n = 1; 2). 从以上分析我们得出, = 0 和 = 1(0) 之间的区域是惟一的稳定域, 由 图 2 中 的 有 色 区 域 表 示. 其 中 对 于 1(0) 来 说 统的平衡点的稳定性如下. , 平衡点 x 0 = 1) 如果jbj < a k bM (0) a bk 对于任 意 > 0 都是渐近稳定的. 因为当jbj < a 时, 由 k (20) 式知 v 的值为虚数, 即 v = iw(w > 0). 由于判 定稳定性的临界曲线是特征值曲线, 即 = iv, 若 v 为虚数, 则 = i(iw). 因此特征方程 (15) 所有的 特征根都存在负实部, 即所有 1(n) 和 2(n) 都是临 界曲线, 因此整个参数范围内都是稳定的. 2) 如 果jbj > a k , 存 在 一 系 列 的 值, 当 = (n), n = 0; 1; 2; 时, 特征方程 (16) 有一 对纯虚根iv: (k < 0), 平 衡 点 x 1⃝如 果 b > a k 0 = 当 2 (0; (0)) 时 是 渐 近 稳 定 的, 当 2 bM (0) a bk ( (n); (n + 1)) 时是不稳定的; 根据 (15) 式, 如果 b > a , = 0 时特征值有负实部; 同样地, 根据 k (22), (23) 和 (30) 式, 如同前面的讨论, = 0 和临 界曲线 1(0) 之间的区域是惟一的稳定域, 因此当 2 (0; (0)) 时, 特征方程 (15) 所有的根都有负实 部; 因为jbj > a , v 的值为实数, 根据 (20) 式, 临 k 界曲线的特征值为 = iv, 因此 = (0) 时, 特征 030502-4 ⊲⊲⊲⊲⊲⊲⊲⊲⊲bt⊳-5
    物 理 学 报 Acta Phys. Sin. Vol. 66, No. 3 (2017) 030502 2⃝如果 b < a k 方程 (15) 所有的根除了iv 都有负实部, 其余的临 界曲线 1(n), 2(n)(n = 0; 1; 2; ) 都具有正实部; , 平衡点 x bM (0) a bk 对于所有 0 = a > 0 都是不稳定的, 因为 b < , 由 (15) 式, 当 k = 0 时, 特征值只有正实部, 以及由 (30) 式, 这里 a 存在至少一个特征值有正实部, 因此, 如果 b < , k 对于任意 > 0 的整个参数空间, 平衡点都是不稳 定的. 4 数值仿真 我们使用龙格库塔方法对系统方程 (1) 进行数 值求解. 通过选择不同的参数值可得到系统不同的 动态范围. 下面我们保持忆阻参数不变, 研究当参 数 a, b, 取不同值时, 系统的动态变化. 4.1 系统随参数 a 的变化 这 里 保 持 忆 阻 参 数 的 值 不 变 以 及 令 b = 1, = 1:61, 改变参数 a 的值. 当参数 a 的值在适当的 范围内变化时, 我们发现系统会呈现出不同的运动 轨迹. 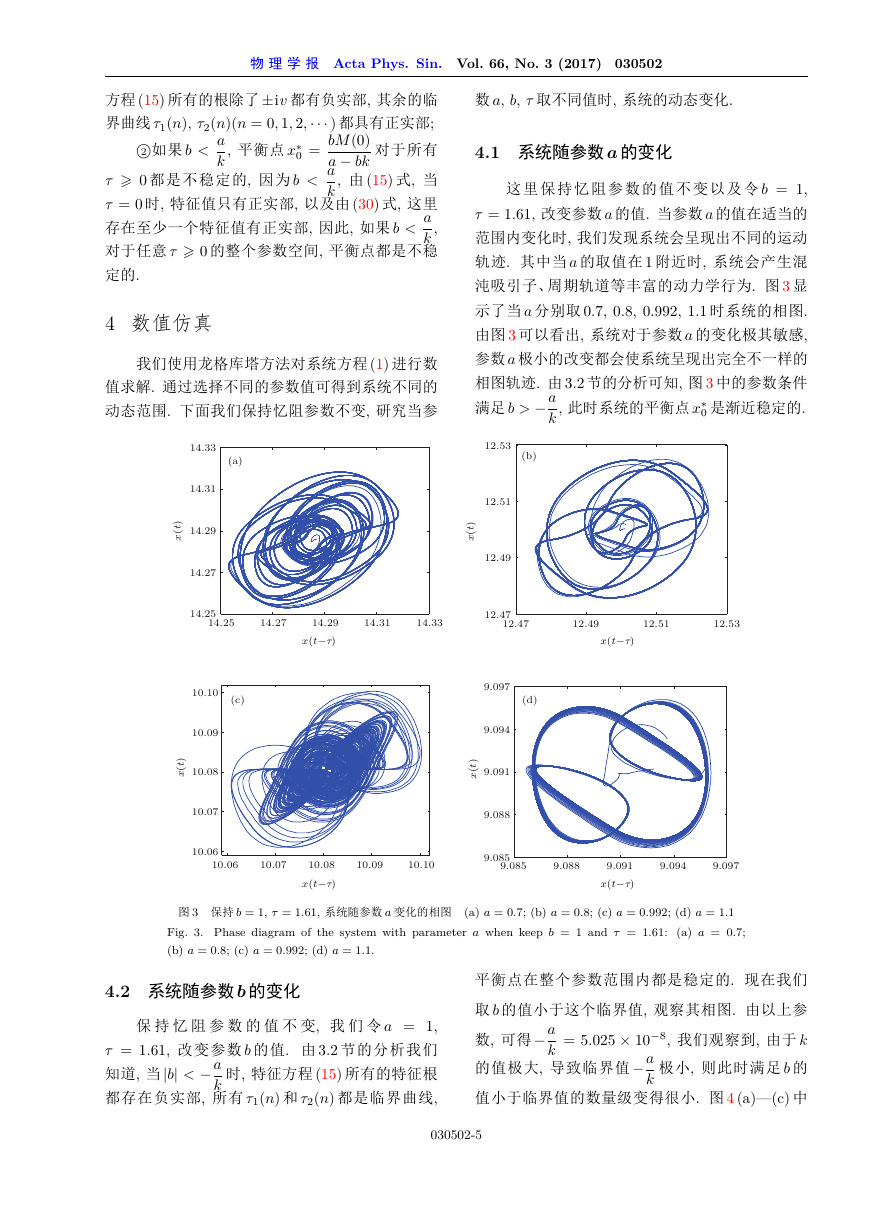其中当 a 的取值在 1 附近时, 系统会产生混 沌吸引子、周期轨道等丰富的动力学行为. 图 3 显 示了当 a 分别取 0.7, 0.8, 0.992, 1.1 时系统的相图. 由图 3 可以看出, 系统对于参数 a 的变化极其敏感, 参数 a 极小的改变都会使系统呈现出完全不一样的 相图轨迹. 由 3.2 节的分析可知, 图 3 中的参数条件 满足 b > a 0 是渐近稳定的. k , 此时系统的平衡点 x 图 3 保持 b = 1, = 1:61, 系统随参数 a 变化的相图 (a) a = 0:7; (b) a = 0:8; (c) a = 0:992; (d) a = 1:1 Fig. 3. Phase diagram of the system with parameter a when keep b = 1 and = 1:61: (a) a = 0:7; (b) a = 0:8; (c) a = 0:992; (d) a = 1:1. 4.2 系统随参数 b 的变化 保 持 忆 阻 参 数 的 值 不 变, 我 们 令 a = 1, = 1:61, 改变参数 b 的值. 由 3.2 节的分析我们 知道, 当jbj < a 时, 特征方程 (15) 所有的特征根 k 都存在负实部, 所有 1(n) 和 2(n) 都是临界曲线, 平衡点在整个参数范围内都是稳定的. 现在我们 取 b 的值小于这个临界值, 观察其相图. 由以上参 = 5:025 10 数, 可得 a 8, 我们观察到, 由于 k k 的值极大, 导致临界值 a 极小, 则此时满足 b 的 k 值小于临界值的数量级变得很小. 图 4 (a)—(c) 中 030502-5 (a)(b)(c)(d)14.2514.2714.2914.3114.33⊲⊲⊲⊲⊲x↼t֓τ↽x↼t֓τ↽x↼t֓τ↽x↼t֓τ↽x↼t↽12.4712.4912.5112.53⊲⊲⊲⊲x↼t↽10.0610.0710.0810.0910.1010.0610.07⊲10.0910.10x↼t↽9.0859.0889.0919.0949.0979.0859.0889.0919.0949.097x↼t↽
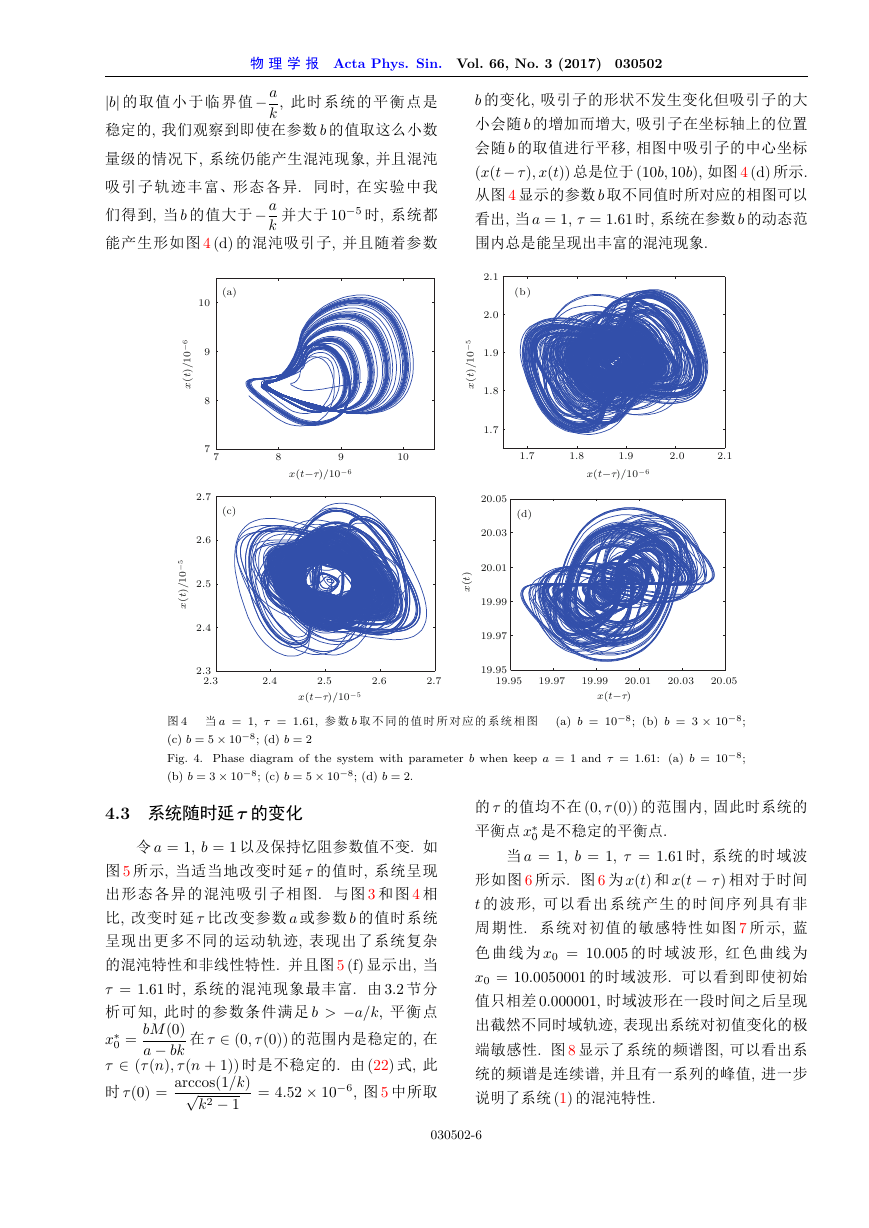
    物 理 学 报 Acta Phys. Sin. Vol. 66, No. 3 (2017) 030502 jbj 的取值小于临界值 a , 此时系统的平衡点是 k 稳定的, 我们观察到即使在参数 b 的值取这么小数 量级的情况下, 系统仍能产生混沌现象, 并且混沌 吸引子轨迹丰富、形态各异. 同时, 在实验中我 们得到, 当 b 的值大于 a 5 时, 系统都 k 能产生形如图 4 (d) 的混沌吸引子, 并且随着参数 并大于 10 b 的变化, 吸引子的形状不发生变化但吸引子的大 小会随 b 的增加而增大, 吸引子在坐标轴上的位置 会随 b 的取值进行平移, 相图中吸引子的中心坐标 (x(t ); x(t)) 总是位于 (10b; 10b), 如图 4 (d) 所示. 从图 4 显示的参数 b 取不同值时所对应的相图可以 看出, 当 a = 1, = 1:61 时, 系统在参数 b 的动态范 围内总是能呈现出丰富的混沌现象. 图 4 当 a = 1, = 1:61, 参 数 b 取 不 同 的 值 时 所 对 应 的 系 统 相 图 (a) b = 10 (c) b = 5 10 Fig. 4. Phase diagram of the system with parameter b when keep a = 1 and = 1:61: (a) b = 10 (b) b = 3 10 8; (c) b = 5 10 8; (d) b = 2. 8; (d) b = 2 8; (b) b = 3 10 8; 8; 4.3 系统随时延 的变化 令 a = 1, b = 1 以及保持忆阻参数值不变. 如 图 5 所示, 当适当地改变时延 的值时, 系统呈现 出形态各异的混沌吸引子相图. 与图 3 和图 4 相 比, 改变时延 比改变参数 a 或参数 b 的值时系统 呈现出更多不同的运动轨迹, 表现出了系统复杂 的混沌特性和非线性特性. 并且图 5 (f) 显示出, 当 = 1:61 时, 系统的混沌现象最丰富. 由 3.2 节分 析可知, 此时的参数条件满足 b > a/k, 平衡点 在 2 (0; (0)) 的范围内是稳定的, 在 x 0 = 2 ( (n); (n + 1)) 时是不稳定的. 由 (22) 式, 此 6, 图 5 中所取 时 (0) = = 4:52 10 bM (0) a bk arccos(1/k) p k2 1 的 的值均不在 (0; (0)) 的范围内, 固此时系统的 平衡点 x 0 是不稳定的平衡点. 当 a = 1, b = 1, = 1:61 时, 系统的时域波 形如图 6 所示. 图 6 为 x(t) 和 x(t ) 相对于时间 t 的波形, 可以看出系统产生的时间序列具有非 周期性. 系统对初值的敏感特性如图 7 所示, 蓝 色 曲 线 为 x0 = 10:005 的 时 域 波 形, 红 色 曲 线 为 x0 = 10:0050001 的时域波形. 可以看到即使初始 值只相差 0.000001, 时域波形在一段时间之后呈现 出截然不同时域轨迹, 表现出系统对初值变化的极 端敏感性. 图 8 显示了系统的频谱图, 可以看出系 统的频谱是连续谱, 并且有一系列的峰值, 进一步 说明了系统 (1) 的混沌特性. 030502-6 x↼t֓τ↽⊳-6x↼t֓τ↽⊳-5x↼t֓τ↽x↼t֓τ↽⊳-6(a)(b)(c) (d)78910x↼t↽⊳-6x↼t↽⊳-5x↼t↽⊳-51.71.81.92.02.11.71.81.92.02.1⊲2.42.52.62.7⊲⊲⊲⊲⊲19.9519.9719.9920.0120.0320.0519.9519.9719.9920.0120.0320.05x↼t↽
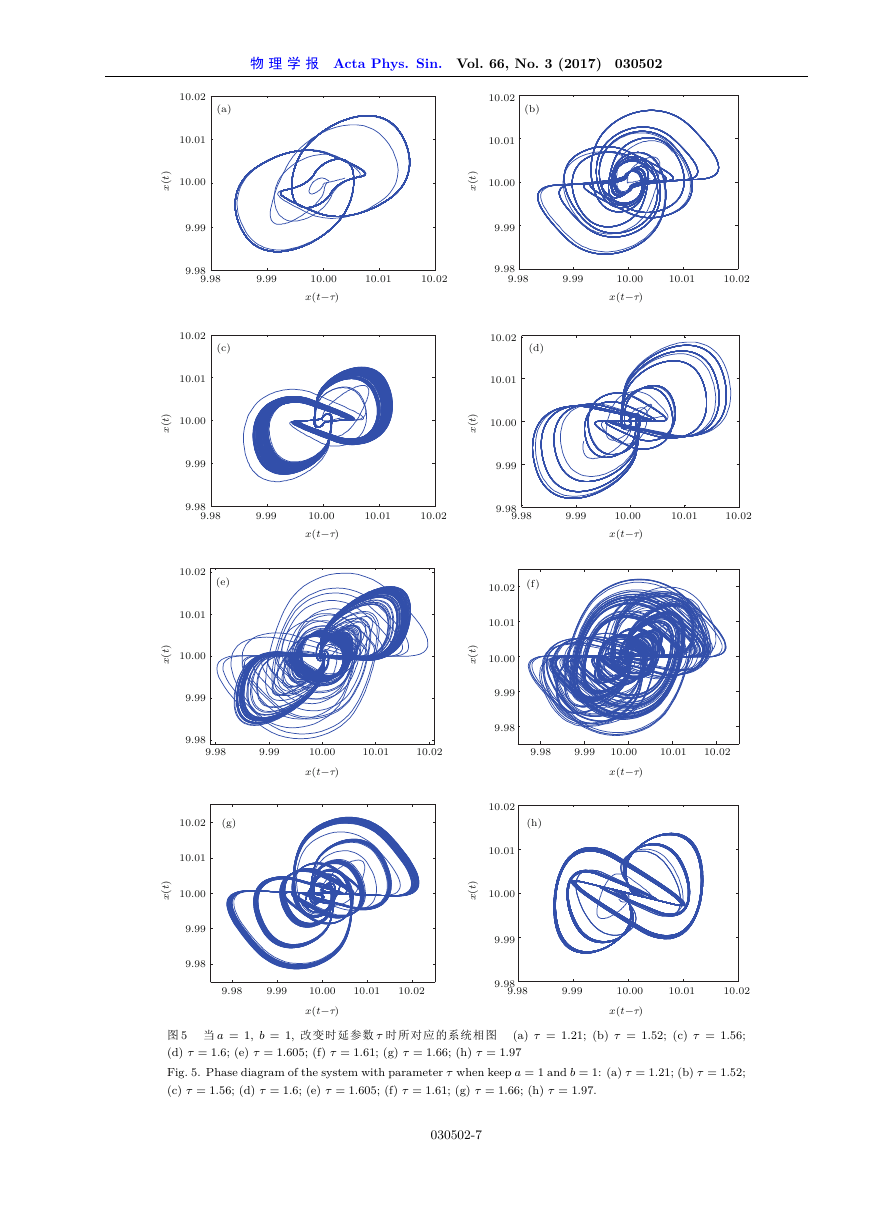
    物 理 学 报 Acta Phys. Sin. Vol. 66, No. 3 (2017) 030502 图 5 当 a = 1, b = 1, 改变时延参数 时所对应的系统相图 (a) = 1:21; (b) = 1:52; (c) = 1:56; (d) = 1:6; (e) = 1:605; (f) = 1:61; (g) = 1:66; (h) = 1:97 Fig. 5. Phase diagram of the system with parameter when keep a = 1 and b = 1: (a) = 1:21; (b) = 1:52; (c) = 1:56; (d) = 1:6; (e) = 1:605; (f) = 1:61; (g) = 1:66; (h) = 1:97. 030502-7 x↼t֓τ↽x↼t֓τ↽x↼t֓τ↽x↼t֓τ↽x↼t֓τ↽x↼t֓τ↽x↼t֓τ↽x↼t֓τ↽9.989.9910.0110.029.989.9910.0010.0010.0010.0010.0010.0010.0010.0010.0110.02x↼t↽x↼t↽x↼t↽x↼t↽x↼t↽x↼t↽x↼t↽x↼t↽9.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0110.029.989.9910.0010.0010.0010.0010.0010.0010.0010.0010.0110.029.989.9910.0110.02(a) (c)(e)(g)(b) (d)(f)(h)
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料