logo资料库

光学计算题及答案.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.98M 资料格式：doc 举报 版权申诉
第1页 / 共43页
第2页 / 共43页
第3页 / 共43页
第4页 / 共43页
第5页 / 共43页
第6页 / 共43页
第7页 / 共43页
第8页 / 共43页
资料共43页，剩余部分请下载后查看
    4001．在杨氏实验装置中，光源波长为 640 nm，两狭缝间距为 0.4 mm，光屏离狭缝的距离为 50 cm。试求：⑴ 光屏上第 1 亮 条纹和中央亮条纹之间的距离；⑵ 若 P 点离中央亮条纹为 0.1 mm，则两束光在 P 点的相位差是多少？ 4002．已知铯的逸出功为 1.88 eV，现用波长为 300 nm 的紫外光照射，试求光电子的初动能和初速。 4003．波长为 546.1 nm 的平行光垂直地射在 1 mm 宽的缝上，若将焦距为 100 cm 的透镜紧贴于缝的后面，并使光聚焦到屏上， 试问衍射图样的中央到 ⑴ 第一最大值；⑵第一最小值；⑶ 第三最小值的距离分别为多少？ 4004．高 6 cm 的物体距凹面镜顶点 12 cm ，凹面镜的焦距是 10 cm ，试求像的位置及高度。 4005．请按以下要求设计一块光栅：① 使波长 600 nm 的第二级谱线的衍射角小于 30°，并能分辨其 0.02 nm 的波长差；② 色 散尽可能大；③ 第三级谱线缺级。则该光栅的缝数、光栅常量、缝宽和总宽度分别是多少？用这块光栅总共能看到 600 nm 的 几条谱线？ 4006．两个尼科耳 1N 和 2N 的夹角为 60°，在它们之间放置另一个尼科耳 3N ，让平行的自然光通过这个系统。假设各尼 科耳对非常光均无吸收，试问 3N 和 1N 的透振方向的夹角为何值时，通过系统的光强最大？设入射光强为 02I ，求此时所能 通过的最大光强。 4007．波长为 500 nm 的单色平行光射在间距为 0.2 mm 的双狭缝上，通过其中一个缝的能量为另一个的 2 倍，在离狭缝 50 cm 的光屏上形成干涉图样，试求干涉条纹的间距和可见度。 4008．在两个共轴平行放置的透振方向正交的理想偏振片之间，有一个共轴平行放置的理想偏振片以匀角速度  绕光的传播方 向旋转，若入射到该系统的平行自然光强为 0I ，则该系统的透射光强为多少？ 4009．在电子显微镜中，电子受到 90 kV 的电压加速，如要观察到物质的分子结构（其大小为 10 - 9 cm 数量级），则显微镜的 数值孔径应该多大（不考虑相对论效应）？ 4010．有一理想光具组置于空气中，如图所示，已知焦距 算法求像的位置、大小和倒正。 f     f 2 cm ，物高为 1cm，物距为 6cm。分别用作图法和计 4011.一束光强为 I 的自然光，连续通过两个尼科尔主截面成 600 角的偏振元件，若在他们中间插入一块水晶的λ/4 片，其主截面 平分上述夹角，试问 ： 1. 通过λ/4 片光的偏振态？ 2. 通过第 2 个尼科尔 2N 的光强是入射光强的多少倍？ 4012.波长为 300nm 的光照涉到钾表面上时，发出光电子的最大动能为 2.0eV，试求 ： 1. 入射光中每个光子的能量。 2. 钾的脱出功。 3. 若入射光的波长为 395nm,遏制电压是多少？ （普朗克常数 h＝6.626×10－34Js，电子电荷 e≈1.6×10-19C，真空中光速 c=3×108m/s） 4013.钠光通过宽为 0.2mm 的狭缝后,投射到与缝相距 300cm 的照相版上，所得的第二最小距离为 0.885cm，则钠光的波长为多少？ 若改用波长为 0.1nm 的 X 射线作此实验，则版上的这两个最小值之间的距离是多少？ 4014.波长为 330nm 的紫外光，入射到脱出功为 2.2eV 的金属表面上，试求光电子从金属表面打出时的初动能和初速（h≈6.6× 10－34Js，m≈9.1×10－31kg，e≈1.6×10-19C）。 4015.迈克尔逊干涉仪的反射镜 2M 移动 0.25mm 时，看到条纹移动过的数目为 1000 个，设光为垂直入射，所求光源的波长。 4016．两个薄凸透镜 L1 和 L2 的孔径都是 4cm，L1 的焦距为 8cm，L2 的焦距为 3cm，L2 的焦距为 3cm，L2 在 L1 之后 5cm , 对于平行于光轴入射的光线，求系统的有效光阑，入射光瞳和出射光瞳。 4017 将焦距 f’=25cm 的薄透镜切取宽度为 a 的中央部分，且满足 a<
    a 4018．一平面透射光栅的光栅常数 d=1.5mm,宽度 D=3cm，一束准单色光以 300 角射到光栅上，已知光栅后透镜只能接受衍射角 小于 600 角的衍射光，在透镜后焦面上接受衍射光谱。试求: (1).在第一级光谱中能否分辨波长为 500nm 和 500.01nm 的两条相邻谱线？ (2).最多能收到第几级光谱？能分辨的最小波长间隔是多少？ 4019．如图所示的杨氏干涉实验装置中，在加偏振片以前，一单色准直自然光照下，屏上呈现的是一簇明暗相间的等间隔的直 线状条纹。现导入一组偏振片和波片来进行实验，试分析下述五种条件下，屏幕上呈现的条纹的变化。 （1）在狭缝 S 后放置一偏振片 P； （2）在 S 后放一偏振片 P，随后再于 1S 和 2S 之前分别放置偏振片 1P 和 2P ， 1P 与 2P 的透振方向互相正交，P 的透振方 向分别与 1P 、 2P 的透振方向成 45o； （3）若 S 后放置的偏振片 P 的透振方向与狭缝 1S 和 2S 平行，随后以光轴互相正交且与缝平行和垂直的 1/2 波片分别掩遮 1S 和 2S 。 （4）在条件（3）的情况下，把 P 转过π/2； （5）若以 1/4 波片代替 1/2 波片，重新讨论问题（3）和（4）。 S P P1 S1 S2 P2 D 4020． 氦氖激光的单色性为 6×10-10，则其相干长度是多少？ 4021．波长为 500nm 的绿光投射在间距 d 为 0.022cm 的双缝上，在距离 180cm 处的光屏上形成干涉条纹，求两个亮条纹之间的 距离。若改用波长为 700nm 的红光投射到此双缝上，两个亮条纹之间的距离又为多少？算出这两种光第 2 级亮条纹的位置。 4022．在杨氏实验装置中，光源波长为 640nm，两狭缝的间距为 0.4mm 光屏离狭缝的距离为 50cm。试求：（1）光屏上第 1 亮条 纹和中央亮条纹之间的距离；（2）若 P 点离中央亮条纹为 0.1mm，问两束光在 P 点的相位差是多少？（3）求 P 点的光强度和中 央点的强度之比。 4023．把折射率为 1.5 的玻璃片插入杨氏实验的一束光路中，光屏上原来第 5 级两条纹所在的位置变为中央亮条纹，试求插入的 玻璃片的厚度。已知光波长为 6.0 10 m 7 。 4024．波长为 500nm 的单色平行光射在间距为 0.2mm 的双狭缝上。通过其中一个缝的能量为另一个的 2 倍，在离狭缝 50cm 的 光屏上形成干涉图样。求干涉条纹间距和条纹的可见度。 4025．波长为 700nm 的光源与菲涅耳双镜的相交棱之间距离为 20cm，棱到光屏间的距离 L 为 180cm，若所得干涉条纹中相邻亮 条纹的间隔为 1mm，求双镜平面之间的夹角θ。 4026．透镜表面通常镀一层如 MgF2（n=1.38）一类的透明物质薄膜，目的是利用干涉来降低玻璃表面的反射。为了使透镜在可 见光谱的中心波长（550nm）处产生极小的反射，则镀层必须有多厚？ 4027．在两块玻璃之间一边放一条厚纸，另一边相互压紧。玻璃片 l 长 10cm，纸厚为 0.05mm，从 60o 的反射角进行观察，问在 玻璃片单位长度内看到的干涉条纹数目是多少?设单色光源波长为 500nm。 4028．在上题装置中，沿垂直于玻璃片表面的方向看去，看到相邻两条暗纹间距为 1.4mm。已知玻璃片长 17.9cm，纸厚为 0.036mm， 求光波的波长。 4029．波长为 400～600nm 的可见光正射在一块厚度为 哪些波长的光最强。 1.2 10 m 6 ，折射率为 1.5 的薄玻璃片上，试问从玻璃片反射的光中 4030．迈克耳逊干涉仪的反射镜 M2 移动 0.25mm 时，看到条纹移过的数目为 909 个，设光垂直入射，求所用光源的波长。 4031．迈克耳逊干涉仪平面镜的面积为 4 4cm 2 角为多大？ ，观察到该镜上有 20 个条纹。当入射的波长为 589nm 时，两镜面之间的夹 4032．用单色光观察牛顿环，测得某一亮环的直径为 3mm，在它外边第五个亮环的直径为 4.6mm，所用平凸透镜的凸面曲率半
    径为 1.03m，求此单色光的波长。 4033． 在反射光中观察某单色光所形成的牛顿环。其第 2 级亮条环与第 3 级亮条环间距为 1mm，求第 19 和 20 级亮环之间的距 离。 4034．将焦距为 50cm 的会聚透镜中央部分 C 切去，余下的 A、B 两部分仍旧粘起来，C 的宽度为 1cm。在对称轴线上距透镜 25cm 处置一点光源 P，发出波长为 692nm 的红宝石激光，在对称轴线上透镜的另一侧 50cm 处置一光屏，屏面垂直于轴线。 试求： （1）干涉条纹的间距是多少? （2）光屏上呈现的干涉图样是怎样的？ A C B P A B 4037．单色平面光照射到一小圆孔上，将其平面分成半波带。求第 k 个带的半径。若极点到观察点的距离 0r 为 1m，单色光波 长为 450nm，求此时第一半波带的半径。 4038．平行单色光从左向右垂直射到一个有圆形小孔的屏上，舍此孔可以像照相机光圈那样改变大小。问：（1）小孔半径应满 足什么条件时，才能使得此小孔右侧轴线上距小孔中心 4m 的 P 点的光强分别得到极大值和极小值；（2）P 点最亮时，小孔 直径应为多大？设此光的波长为 500nm。 4039．波长为 632.8nm 的平行光射向直径为 2.76mm 的圆孔，与孔相距 1m 处放一屏。试问; (1)屏上正对圆孔中心的 P 点是亮点还是暗点？ （2）要使 P 点变成与（1）相反的情况，至少要把屏幕分别向前或向后移动多少？ 4040．平面光的波长为 480nm，垂直照射到宽度为 0.4mm 的狭缝上，会聚透镜的焦距为 60cm。分别计算当缝的两边到 P 点的相 位差为π/2 和π/6 时，P 点离焦点的距离。 4041．白光形成的单缝衍射图样中，其中某一波长的第三个次最大值与波长为 600nm 的光波的第二个次最大值重合。求该光波 的波长。 4042．波长为 546.1nm 的平行光垂直地射在 1mm 宽的缝上，若将焦距为 100cm 的透镜紧贴于缝的后面，并使光聚焦到屏上，问 衍射图样的中央到（1）第一最小值；（2）第一最大值；（3）第三最小值的距离分别为多少？ 4043．以纵坐标表示强度，横坐标表示屏上的位置，粗略的画出三缝的夫琅和费衍射（包括缝于缝之间的干涉）图样。设缝宽 为 b，相邻缝间的距离为 d，d=3b。注意缺级问题。 4044．用可见光（760～400nm）照射光栅时，一级光谱和二级光谱是否重叠？二级和三级怎样？若重叠，则重叠范围是多少？ 4045．用每毫米内有 400 条刻痕的平面透射光栅观察波长为 589nm 的钠光谱。试问：（1）光垂直入射时，最多能观察到几级光 谱？（2）光以 300 角入射时，最多能观察到几级光谱？ 4046．波长为 0.00147nm 的平行 X 射线射在晶体界面上，晶体原子层的间距为 0.28nm，问光线与界面成什么角度时，能观察到 二级光谱。 4047．有三条彼此平行的狭缝，宽度均为 b，缝距分别为 d 和 2d，试用振幅矢量叠加法证明正入射时，夫琅和费衍射强度公式 为 I  I 0 式中 u   sin   cos 4   cos6     2 u 3 2 cos 2  sin 2 u        ,   b d sin  4048．一宽度为 2cm 的衍射光栅上刻有 12000 条刻痕。一波长=500nm 的单色光垂直投射，将折射率为 1.5 的劈状玻璃片置 于光栅前方，玻璃片的厚度从光栅的一端到另一端由 1mm 均匀变薄到 0.5mm，试问第一级主最大方向的改变了多少？ 4049．一平行单色光投射于衍射光栅上，其方向与光栅的法线成θ0 角，在和法线成 110 和 530 角的方向上出现第一级谱线，且 位于法线的两侧。 （1）试求入射角θ0； （2）试问为什么在法线的两侧能观察到一级谱线，而在法线的同侧则能观察到二级谱线? 4050．波长为 600nm 的单色光正入射到一透明平面光栅上，有两个相邻的主最大分别出现在 sin  1  0.2 和 sin  2  0.3
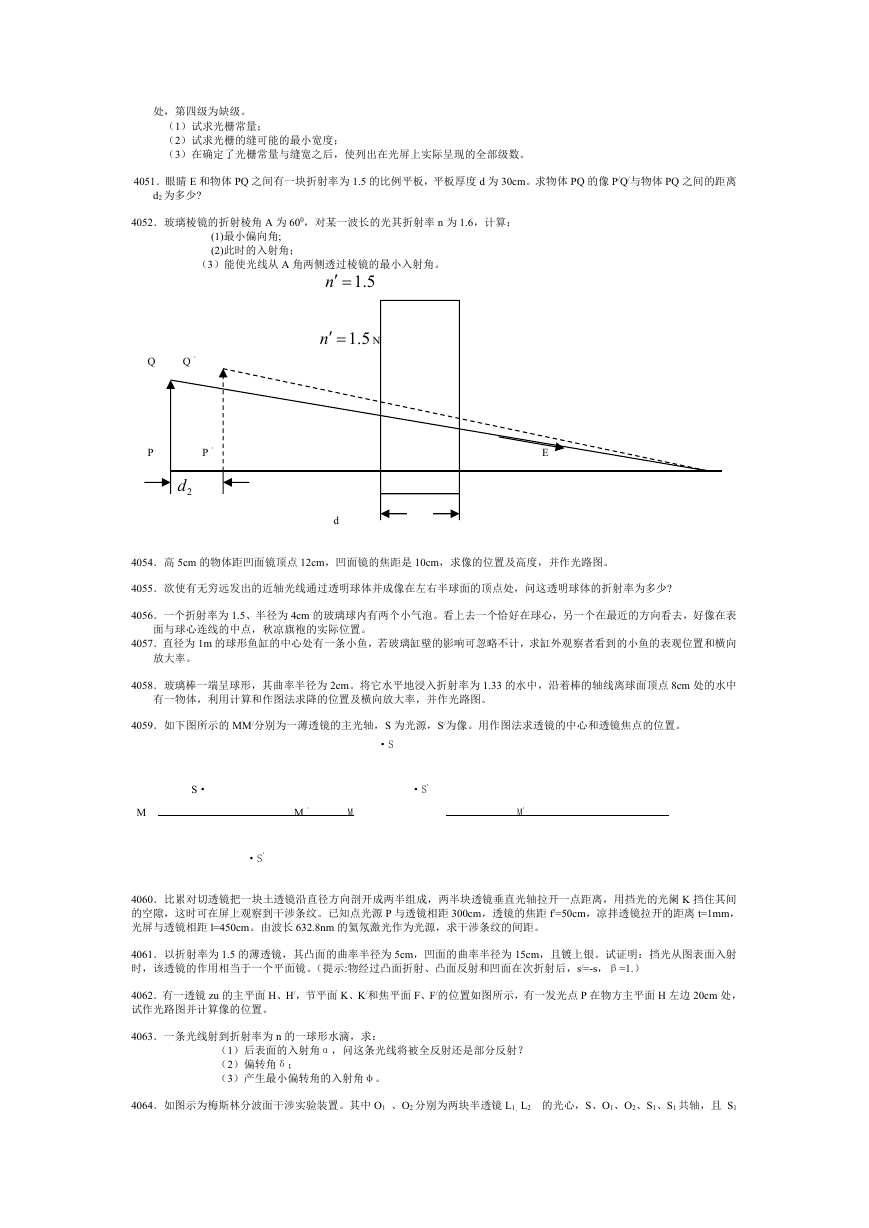
    处，第四级为缺级。 （1）试求光栅常量； （2）试求光栅的缝可能的最小宽度； （3）在确定了光栅常量与缝宽之后，使列出在光屏上实际呈现的全部级数。 4051．眼睛 E 和物体 PQ 之间有一块折射率为 1.5 的比例平板，平板厚度 d 为 30cm。求物体 PQ 的像 P/Q/与物体 PQ 之间的距离 d2 为多少? 4052．玻璃棱镜的折射棱角 A 为 600，对某一波长的光其折射率 n 为 1.6，计算： (1)最小偏向角; (2)此时的入射角； （3）能使光线从 A 角两侧透过棱镜的最小入射角。 n  1.5 Q Q‘ P P‘ 2d n  1.5 N d E 4054．高 5cm 的物体距凹面镜顶点 12cm，凹面镜的焦距是 10cm，求像的位置及高度，并作光路图。 4055．欲使有无穷远发出的近轴光线通过透明球体并成像在左右半球面的顶点处，问这透明球体的折射率为多少? 4056．一个折射率为 1.5、半径为 4cm 的玻璃球内有两个小气泡。看上去一个恰好在球心，另一个在最近的方向看去，好像在表 面与球心连线的中点，秋凉旗袍的实际位置。 4057．直径为 1m 的球形鱼缸的中心处有一条小鱼，若玻璃缸壁的影响可忽略不计，求缸外观察者看到的小鱼的表观位置和横向 放大率。 4058．玻璃棒一端呈球形，其曲率半径为 2cm。将它水平地浸入折射率为 1.33 的水中，沿着棒的轴线离球面顶点 8cm 处的水中 有一物体，利用计算和作图法求降的位置及横向放大率，并作光路图。 4059．如下图所示的 MM/分别为一薄透镜的主光轴，S 为光源，S/为像。用作图法求透镜的中心和透镜焦点的位置。 S· ·S ·S¹ M M‘ M M¹ ·S¹ 4060．比累对切透镜把一块土透镜沿直径方向剖开成两半组成，两半块透镜垂直光轴拉开一点距离，用挡光的光阑 K 挡住其间 的空隙，这时可在屏上观察到干涉条纹。已知点光源 P 与透镜相距 300cm，透镜的焦距 f/=50cm，凉拌透镜拉开的距离 t=1mm， 光屏与透镜相距 l=450cm。由波长 632.8nm 的氦氖激光作为光源，求干涉条纹的间距。 4061．以折射率为 1.5 的薄透镜，其凸面的曲率半径为 5cm，凹面的曲率半径为 15cm，且镀上银。试证明：挡光从图表面入射 时，该透镜的作用相当于一个平面镜。（提示:物经过凸面折射、凸面反射和凹面在次折射后，s/=-s，β=1.） 4062．有一透镜 zu 的主平面 H、H/，节平面 K、K/和焦平面 F、F/的位置如图所示，有一发光点 P 在物方主平面 H 左边 20cm 处， 试作光路图并计算像的位置。 4063．一条光线射到折射率为 n 的一球形水滴，求： （1）后表面的入射角α，问这条光线将被全反射还是部分反射？ （2）偏转角δ； （3）产生最小偏转角的入射角φ。 4064．如图示为梅斯林分波面干涉实验装置。其中 O1 、O2 分别为两块半透镜 L1、L2 的光心，S、O1、O2、S1、S1 共轴，且 S1
    S2=l。 （1）试证来自 L1 和 L2 两端的光束到达 P 点的光程差δ=l-（S1P+ S2P）； （2）定性讨论语轴线垂直的光屏上接收到的干涉图样的特点。 4065、把杂质扩散到玻璃中可以增大比玻璃的折射率，这就有可能造出一个厚度均匀的透镜。已知圆板半径为 R，厚度为 d（如 图所示），求沿半径变化的折射率年 n(r)，它会使从 A 点发出的光线传播到 B 点。假定这个薄透镜，d《a，d《b. 4066．一弯凸透镜两个表面的半径 r1 和 r2 分别为-20cm 和-15cm，折射率为 1.5，在 r2 的凸面镀银。在距 r1 球面左侧 40cm 处的主 轴上置一高为 1cm 的物，试求最后成像的位置和像的性质。 4067．把人眼的晶状体看成距视网膜 2cm 的一个简单透镜。有人看清楚距离在 100cm 到 300cm 间的物体。试问： （1）此人看清远点和近点时，眼睛透镜的焦距是多少？ （2）为看清楚 25cm 远的物体，须佩戴怎样的眼镜？ 4068．一显微镜具有三个物镜和两个目镜。三个五镜的焦距分别为 16mm、4mm 和 1.9mm，两个目镜的放大本领分别为 5 和 10 倍。设三个物镜造成的像都能落在相距为 160mm 处，问这显微镜的最大和最小的发送那个大本领各为多少？ 4069．一显微镜物镜焦距为 0.5cm，目镜焦距为 2cm，两镜间距为 22cm。观察者看到的像在无穷远处。试求物体的距离和显微 镜的放大本领。 4070．组成题下图的简单望远镜中各薄透镜的参数为 L1：f1=10cm，D1=4cm；L2：f2=2cm，D2=1.2cm;L3:f3=2cm，D3=1.2cm。计 算该系统出射光线光瞳的位置和大小。 4071．有一光阑直径为 5cm，放置在薄透镜后 3cm 处。透镜的焦距为 5cm，孔径为 6cm。现有一高为 3cm 的物 PQ 置于透镜前 12cm 处。要求： （1）计算对主轴上 P 点的入射光瞳的大小和位置； （2）找到像的位置； （3）作光路图。 4072．如图所示中的 H、H/为光具组的主点，F、F/为焦点，E 为对于物点 P 的入射光瞳，EO 为其半径。已知 EO=2cm，HP=20cm， HF=15cm，HO=5cm，H/F/=15cm，HH/=5cm，物长 PQ=0.5cm。作光路图并计算： （1）像的位置； （2）像长； （3）入射孔径角； （4）P 点的出射光通半径和出射孔径角。 4073．一灯（可认为是点光源）悬在圆桌中央的上空，桌的半径为 R，为了使桌的边缘能得到最大的亮度，灯应悬在离桌面中 心多高处？ 4074．焦距为 20cm 的薄透镜，放在发光强度为 15cd 的点光源之前 30cm 处。在透镜后面 80cm 处放一屏，在屏上得到明亮的圆 斑。求不计透镜中光的吸取时，圆斑的中心强度。 4075．一长为 5cm 的线状物体放在一照相机镜头前 50cm 处，在底片上形成的像长为 1mm。若底片后移 1cm，则像的弥散斑宽 度为 1mm。试求照相机镜头的 F 数。 4076．某玻璃在靠近钠光的黄色双谱线（某波长分别为 589nm 和 589.6nm）附近的色散率 dn/dλ为-360cm-1，求有此种玻璃制成的能分辨钠光双谱线的三棱镜，底边宽度应小于多少？ 4077．设计一块光栅，要求（1）使波长 600nm 的第二级谱线的衍射角小于 300，能分辨其 0.02nm 的波长差；（2）色散尽可能 大；（3）第三级谱线缺级。求出其缝宽、缝数、光栅常量和总长度。用这块光栅总共能看 600nm 的几条谱线？ 4078．若要求显微镜能分辨相距 0.000375mm 的两点，用波长为 550nm 的可见光照明。试求： （1）此显微镜物镜的数值孔径； （2）若要求此两点放大后的视角为 2/，则显微镜的放大本领是多少？ 4079．平行光垂直投射于宽度为 4cm 的理想透明平面光栅上，一直在衍射角为 600 的方向上的角色散为 0.5×10-2rad/nm，试求光 栅在该方向上最大处的分辨本领 P？ 4080．氦氖激光器发出的波长为 632.8nm、截面直径为 2mm 的激光束投向月球。已知月球和地面的距离为 3.76×105km，试问 在月球上得到的光斑的直径有多大？如果这个激光经扩束器后截面直径分别为 2m 和 5m，再发向月球，试问在月球表面上光斑 直径各为多少？ 4081．用一架照相机在离地面 200km 的高空拍摄地面上的物体，如果要求它能分辨地面上相距 1m 的两点，照相机镜头的口径 至少要多大？设感光的波长为 550nm。 4082．已知月地距离約为 3.8×105km，用上海天文台的口径为 1.56m 天体测量望远镜能分辨月球表面上的两点的最小距离为多 少？设波长为 555nm。 4083．为了分辨第二级钠光谱的双线（589nm、589.6nm），长度为 15cm 的平面光栅常量应为多少？ 4084．试确定下面两列光波
    E 1 E 2    A e  0 x  A e  0 x cos sin  t   t    kz kz     e e y y 的偏振态。  cos t   sin t    kz kz       / 2    / 2  4085．为了比较两个被自然光照射的表面的亮度，对其中一个表面直接进行观察，另一个表面通过两块偏振片来观察，两偏振 片的透振方向的夹角为 60o，若观察到两表面的亮度相同，则两表面实际的亮度比是多少？已知光通过每一块偏振片后损失入射 光能量的 10%。 4086．在两个正交的理想偏振片之间有一个偏振片以匀角速度 w 绕光的传播方向旋转（见图），若入射的自然光强为 I0，试证明 透射光强为 I  I N1  0 1 cos 4  t  /16 ω N2 4087．线偏振光入射到折射率为 1.732 的玻璃片上,入射角是 600,入射光的电矢量与入射面成 300 角.求分界面上反射的光强的百分 比. 4088．线偏振光垂直入射到一块光轴平行于表面的方解石波片上,光的振动面的波片的主截面成 300 角。求（1）投射出来的寻常 光和非常光的相对强度为多少？（2）用钠光入射时如要产生 900 的相位差，波片的厚度用为多少？（λ=589nm） 4089．有一块平行石英片是沿平行光轴方向切出的。要把它切成一块黄光的 1/4 波片，问这块石英片应切多厚？石英片的 ne=1.552, no=1.543, λ=589.3nm. 4090.线偏振光垂直入射到一块表面平行与光轴的双折玻片,光的振动面和 玻片光轴成 250 角,问玻片中的寻常光和非常光投射 出来的相对强度如何? 4091．一束偏振光,(1)垂直入射到 1/4 玻片上, 求投射光的偏振状态;(2) 垂直入射到 1/8 玻片上, 求投射光的偏振状态. 4092.试证明一束左旋偏振光，当他们的振幅相等时，合成的光是偏振光。 4093.设一方解石波片沿平行光轴方向切出，其厚度为 0.0343mm，放在两个正交的尼克耳棱镜间。平行光束经过第一尼克耳棱镜 后，垂直地射到波片上，对于钠光（589.3nm）而言。晶体的折射率为 n0=1.658, ne=1.486.问通过第二尼克耳棱镜后，光束发生 的干涉是加强还是减弱？如果两个尼科耳棱镜的主截面是互相平行的，结果又如何？ 4094．厚度为 0.025mm 的方解石波片，其表面平行与ⅰ轴，放在两个正交的尼科尔棱镜之间，光轴与两个尼科尔各成 450。如 果第一个尼科尔的光是波长为 400-760nm 的可见光，问透过第二个尼科尔的光中，少了哪些波长的光？ 4095．如图 5.22 所示装置中，S 为单色光源，置于透镜 L 的焦点处，P 为起偏器，Ｌ１为此单色光的１／４波片，其光轴与偏振 器的透振方向成 a 角，Ｍ为平面反射镜。已知入射到偏振光的光束强度为 Io，试通过分析光束经过个元件后的光振动状态，求出 光束返回后的光强Ｉ。个元件对光束损耗可忽略不计。 4096．一束椭圆偏振光沿 z 方向传播，通过一个线起偏器。当起偏器透振方向沿 x 方向时，透射强度最大，其值为 1.5I0；当透 振方向沿 y 方向时，透射强度最小，其值为 I0.(1)当透振方向与 x 轴θ成时，投射强度为多少？（２）使原来的光束先通过一个 1/4 波片再通过线起偏器,1/4 波片的轴沿 x 方向.现在发现,当起偏器透光轴与 x 轴成 300 角时，透过两个元件的光强最大，求光 强的最大值，并确定入射光强中非偏振成分占多少？ 4097．有下列几个未加标明的光学元件：（1）两个线偏振器；（2）一个 1/4 波片；（3）一个半波片；（4）一个圆偏振器。除了一 个光源和一个光屏外不借助其他光学仪器，如何鉴别上述各个元件。 4098．一束汞绿光以 600 角入射到磷酸二氢钾（KDP）晶体表面，晶体的 no=1.512,ne=1.470,设光轴与晶面平行，并垂直于入射面， 试求晶体中 o 与 e 光的夹角。 4099．通过尼科耳棱镜观察一束椭圆偏振光时，强度随尼科耳棱镜的旋转而改变。当强度为极小值时，在尼科耳棱镜（检偏器） 前插入一块茎 1/4 波片，转动 1/4 波片使它的光轴平行于检偏器的透振方向，再把检偏器沿顺时针方向转动 200 就完全消光。问 （1）该椭圆偏振光是右旋还是左旋的？（2）椭圆长短轴之比是多少？ 4100．某种介质的吸收系数 a 为 0.32cm-1。求透射光强为入射光强的 0.1、0.2、0.5 及 0.8 倍时，该介质的厚度各为多少？ 4101．计算波长为 253.6nm 和 546.1nm 的两条谱线瑞利散射的强度之比。
    4102．一个顶角为 600 的棱镜尤某种玻璃制成，它的色散特性可用柯西公式中的常量 a=1.416，b=1.72×10-10cm2 来表示。将棱镜 的位置放置得使它对 600nm 的波长产生最小偏向角。计算这个棱镜的色散率为多少？ 4103．波长为 0.07nm 的 X 射线，其折射率比 1 小 1.60×10-6，只求全反射时，X 射线的掠射角为多大？ 4104．对于波长λ=400nm 的光，某种玻璃的折射率 n=1.63，对于λ/=500nm 的光，其折射率 n/=1.58。假如柯西公式的近似形式 n=a+b/λ2 适用，试求此种玻璃对波长为 600nm 的光色散 dn/dλ值。 4105．试用光的相速度 v 和 dv/dλ来表示群速度 u=dω/dk，再用 v 和 dv/dλ表示群速度 u=dω/dk。 4106．若有一黑体的辐出度等于 5.70W/cm2，试求于该辐射最大光谱强度相对应的波长。 4107．若将恒星表面的辐射近似地看作是黑体辐射，则可用测量λmax 的办法来估计恒星表面的温度。现测得太阳表面的λmax 为 510nm，北极星的λmax 为 350nm，试求它们表面温度。 4108．已知铯的逸出功为 1.88eV，现用波长为 300nm 的紫外光照射，试求光电子的初动能和初速。 4109．波长为 0.1nm 的 X 射线被碳块散射，在散射角为 900 的方向上进行观察。试求： （1）康普顿位移△λ； （2）反冲电子的动能。 4110．在电子显微镜中，电子受到 90kV 的电压加速，如果观察到物质的分子结构（其大小为 10-9cm 数量级），问显微镜的孔径 应该多大？ 4111．（1）一只 100W 灯炮，5%的功率辐射是可见光，假定可见光平均波长为 500nm，则每秒可辐射的可见光光子是多少？（2） 假设灯炮为光点源，可以向各个方向发光，求在距离 2m 处每秒垂直通过单位面积的光子数。 4112．人在黑暗中，眼睛的视网膜如能收到波长为 5.50nm 的最大有效辐射 2×10-18J，就能感知这一光点源。求眼睛这一观察阀 相当于多少个光子？ 4113．一电子束被电压为 V 的电场加速。（1）求电子在加速后的德布罗意波长；（2）求此德布罗意波的相速和群速；（3）把此 德布罗意波射到一块单晶上，如入射光线与晶面成θ角，观察到散射波第一级强度极大值，求晶格常量 d。 4114. 在热核爆炸的火球中，测得瞬时温度为 107K。（1）估算辐射最强的波长；（2）这种辐射最强波长的能量子是多少焦耳？ 4115．（1）计算氢原子最低的四个能级的能量大小，并把它们画成能级图；（2）计算这四个能级之间的跃迁的最小的频率是多 少？ 4116．当波尔描述的氢原子从 n=2 的轨道跃迁到 n=1 的轨道后，问（1）轨道半径变化了多少？（2）能量改变了多少？ 4117．一个电子受激跃迁到氢原子的第三波尔轨道，试计算回到基态时有可能发射的光子的波长。 答案： 4001．解：  y  j r 0 d     y   1  2  j     4002．解： ,  j  0 1. 、 j r 0 d 2        1 0   yd  r  0 2   640 10   7  0.08  cm  ; 50 0.04  4  h      1 1 2  2    4003．解： 1 2 2 m   W 2  m    h W hc  2 2.26 1.6 10      9.11 10  31   W  19  8 19  6.63 10  9 300 10   5 8.9 10   34 3 10   1.6 10     m s /  1.88 2.26   eV   y  tg   f  , tg   sin ,sin   10   1.43 ,sin  k  k  b    1 y 10  1.43  b f   1.43  546.1 10  1  6  100 0.078   b  cm   2  y 1  k   3 y 3  k  b  b f  1   f  3   546.1 10  6  100 0.055   cm  546.1 10  6  100 0.164   cm   1  1
    4004．解：   1  s   1   1 s  s   s s             1 ,  f  f s  s f  s s y     y y  10   12  60  12  12 10     60  cm  15000  条   6  2.4 10   3  mm   2  y    6    30  cm  4005．解：   1  P        jN N ,   j   j  sin  0.8 10    3  600 2 0.02  2 600 10   sin 30   mm  mm 36    2   d sin ,      d j   3      5   0 4 d    3 , b b d 3   15000 2.4 10   3   j m Nd d     2.4 10  600 10   3  6   4, 总共能看到 条谱线。 5 4006．解：  I 1  I 0 , I 3  I 1 2 cos ,  I  欲使 I  I ，须使 m   I 3    2 cos 60  2 2       I 0 2 cos   30 此时所能通过的最大光强为：I m  I 0 4 cos 30   4007．解：   1 y    2  V  r 0 d 2 I 1   I I 1 2 I  2 50 0.2  500 10   6  0.125  cm   2 2 3  0.943     cos   2 9 6 I 0 4008．解：  y   0.61  sin n  n sin u  0.61  u  y  ,   10  8   10  8  150 90 10  3  0.41 10   9  0.61  0.41 10 9  9  0.25 150 V  10  4010．解：由已知得 s/=-6cm f=-2cm f/=2cm 由高斯公式 f//s/+f/s=1 代入数据 2/ s/+(-2)/(-6)=1 得：s/=3cm 又由β=y//y=s//s 代入 s=6cm s/=3cm y=1cm 得： y//1=3/(-6) 所以 y/=-0.5cm,所以像的位置在距像方主点 H/3cm 处，大小为 0.5cm，是倒立的 。 光路图如图所示 Q P F F¹ P¹ Q¹ H¹ H
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料