2007 年第 3 期 Journal of Shenzhen Polytechnic No.3, 2007 深 圳 职 业 技 术 学 院 学 报 基于 ITK 和 VTK 的三维成像实现 王京阳 1，2，周振环 1，赵 明 1 ，王安明 1，3 （1.深圳职业技术学院，广东 深圳 518055；2. 哈尔滨工业大学深圳研究生院，广东 深圳 518055； 3. 南昌大学，江西 南昌 330031） 摘 要：介绍了Fast Marching快速行进图像分割和Marching Cubes步进立方体2种算法的原理，利用ITK的 图像读取与处理功能及VTK在可视化方面的突出能力, 将二者有机地集成起来，通过ITK和VTK实现这2种算 法，最终生成三维立体医学图像。实验结果验证了该方法可以得到病理部位的详细特征，在医学图像三维成像 方面有良好的性能。 关键词：可视化；快速行进；步进立方体 中图分类号：R319 文献标识码：A 文章编号：1672-0318（2007）03-0015-05 医学图像处理与分析涉及的研究内容包括： 键步骤。一方面，它是表达目标的基础，对特征测 医学影像数据获取、医学图像分割、三维可视化 等[1]。医学图像分割从医学图像中提取感兴趣的 器官、组织或病变体，使得医生能够对病变组织 进行定性及定量的分析，从而提高医学诊断的准 确性和科学性。它是实现医学图像三维重建的基 础。可视化技术主要包括面绘制和体绘制技术[2]。 面绘制处理速度快，显示图像形象清晰，其中最 有代表性的是步进立方体算法Marching Cubes。 体绘制技术可以不进行分割直接进行绘制，其好 处在于有利于保留三维医学图像中的细节信息， 但缺点是加大了计算开销，速度很慢，不能进行 实时处理，技术也很复杂。本文详细介绍了快速 行进分割算法Fast Marching[3]和步进立方体算法 Marching Cubes，并使用这些方法对一组CT扫描 图像进行分割处理，重建为三维立体图像。 1 快 速 行 进 分 割 算 法 （ Fast 量有重要的影响；另一方面，图像分割使得更高层 的图像分析和理解成为可能。目前，图像分割在医 学领域得到了广泛的应用。它对医学病变区域提取、 特定组织测量以及实现三维重建有着不可忽视的重 要作用。 医学图像分割主要可以分2类： 1）以区域为基础的方法或者统计性特性方法， 根据一致性原则对图像进行分割，比如区域增长的 方法。这种方法的优势在于考虑到了区域的内部信 息，但是得到的边界不够平滑，呈现锯齿形状。 2）以边界为基础的分割方法，比如Snake方法、 Level Set方法。其中Level Set可变型模型的方法对初 始位置有一定要求，初始的边界对象常常被要求为 大致轮廓，这样可以有效地提升计算速度，同时可 以减少分割错误。 Fast Marching 分割算法是基于几何形变模型的 医学影像分割方法，它是水平集（Level Set）分割 算法的一种。Level Set 分割算法的基本思想是：将 平面闭合曲线隐式地表达为二维曲面函数的水平 集，即具有相同函数值的点集，通过函数曲面的进 化隐式地求解曲线的运动[4]。 Marching，FMM） 图像分割是指把图像分成互不重叠的区域并 提取出感兴趣目标的技术，它是图像处理中的关 收稿日期：2007-04-10 项目来源：深圳市科技计划项目（05KJcd004）；深圳职业技术学院科技发展基金项目（07KJcd005）； 2005 年粤港关键领域重点突破项目 （2005A11304003）资助。 作者简介：王京阳（1983-），男，河南南阳人，在读研究生，研究方向为医学图像处理。 

16 深圳职业技术学院学报 第 6 卷 | Φ 0| +Φ =∇ Ft Level Set 函数的演化满足以下的基本方程： （1） 其中，Φ 为 Level Set 函数，其零水平集表示 ， Φ∇ 目标轮廓曲线，即 表示 Level Set 函数的梯度范数；F 为曲面法线方 向上的速度函数，控制曲线的运动。一般 F 包括 与图像有关的项（如梯度信息等）以及与曲线的 几何形状有关的项（如曲线的曲率等）。 x t |{)( tx ),( }0 Φ Γ = = 虽然上述思想很好，但是对所有的 level sets 都要进行计算，而不单是对与传播前沿相关的零 level Set 进行计算，所以它一个很大的缺点是运 算量很大，对一个 N×N 的图像进行运算，每一 2N )。如果传播前沿的法向 步的运算复杂度为 O( 速度总是保持全正或者全负，那么我们就可以把 上面的问题转化为寻求每个 Level set 的到达时 间，把问题转化为可大大提高运算速度的 Fast Marching 方法。 Fast Marching 方法把问题变为求解方程： ⋅∇T V（x）= )(xΦ （2） 这是一个表示曲线随时间进化的 Eikonal 方 程，还可以表示为如下形式：假设 T(x, y) 为曲线 穿越点(x, y)的时间，曲面 T(x, y) 满足方程： | ∇ FT | = 1 （3） 这个公式简单地说明了到达时间的梯度曲面 与界面的运动速度成反比。接下来利用数值方法 求解 Eikonal 方程： ⋅∇T V（x）= )(xΦ （4） Sethian 指出，要得到式（3）的到达时间 T，等价 于求解以下的二次方程： [max( Dmin( T,0) T,0) max D + + − + 2 2 x x ij ij − y D( ij T,0) 2 + Dmin( + y ])T,0 212 = ij 1 F , i j 。这里 D − 和 D+分别是后向差分和前向差分算子。 ) xT xT − + y y ( ( , , 或 者 1）初始化：①设置活动点：活动点就是所有网 格点中时间 T 固定的点。可以有多种指定方法，本 文所采用的分割算法中设定 T（x，y）=0。②设置 窄带：窄带是指活动点附近的点。在运算时只更新 窄带中的点，以提高计算速度。时间 T（x，y） 1 = 。③标记远点：除了活动点和窄带点外， 所有其他的网格点为远离点，T（x，y）=+∞。 yxF ,( ) 2）循环 ① 循环开始：任取点（x，y），可将其看作窄 带中具有最小时间 T 的点。 ② 将点（x，y）标记为活动点，并将其从窄带 中删除。 ③ 把与点（x，y）相邻接的点做标记：若其邻 接点为活动点，则不改变时间；若其邻接点为窄带 点，则按步骤④更新邻接点的时间；若其邻接点为 远离点，则将该邻接点标记为窄带点，并按步骤④ 更新邻接点的时间。 ④ 若点的到达时间均在我们规定的阈值之下， 则跳转到①，否则结束循环。 2 步进立方体算法（Marching Cubes） Marching Cubes 算法是 W.Lorensen 等人于 1987 年提出的一种三维重建方法，是至今为止最流行的 面显示算法之一。 在三维体数据集中，所有的采样点都位于一个 立体栅格系统中。其最小的单元是以 8 个相邻顶点 构成的立方体。一个体素可以由一个或多个这样的 单元组成。 构型表对一个顶点及给定的该单元点的标量值 组合计算所有可能拓扑状态，拓扑状态数取决于单 元顶点个数及一个顶点可能对应轮廓值内/外关系 数。如果标量值大于轮廓线的标量值，则认为该顶 点在轮廓之内。否则在轮廓之外。例如，如果一个 单元有 4 个顶点，每个顶点可以在轮廓的内部或者 外部，轮廓穿过该单元的方式有 2 4 =16 种。在构型 表中我们对轮廓穿过单元的位置不感兴趣，只关心 它如何经过单元。 物体的表面实际上是一个闭合的灰度等值面， D x + = yxT ) T ,( D x− T= D y + = yxT T ,( ) D y− T= )1 2 − ,( yxT 2 xT + ( − )1 ,1 y − ,1 y ) − xT ( 2 yxT ( , − ) 2 ) 或者 其灰度值称为阈值。在该等值面的内部，所有的象 素灰度值都大于这个阈值，在该等值面的外部，所 有的象素灰度值都小于这个阈值，从而将物体与背 景分开。先从寻找二维图像轮廓线说起。一个单元 有 4 个顶点。每 2 个顶点连接成一条边。每个顶点 Fast Marching 方法的具体步骤： 

第 3 期 王京阳，等：基于 ITK 和 VTK 的三维成像实现 17 的灰度就是该数据点的数值。假设我们选择了一 个灰度阈值 G，根据各顶点的灰度和阈值 G 的关 系将这些顶点分作 2 类，分别用黑、白两色圆点 表示（记作 1 和 0）。对正方形的 4 个边逐个判断， 如果某一个边的 2 个顶点颜色相同，该边上不存 在边缘点；否则，在此边上必有一个边缘点。用 直线将不同边上的边缘点连接起来。对于二维图 像的象素，共有 16 种构型，如图 1 所示。 找表中确定其三角剖分形式，并对相邻正方形一致边 合并，最终产生由小三角形面片镶嵌成的表面轮廓。 三维情况下也存在构型的二义性，如果不加以 解决，就可能导致等值面中出现孔洞，影响最终的 显示效果。一种简单有效的解决办法是对产生二义 性的构型添加附加的互补状态。 3 三维分割算法实现过程及实验 构型0 构型1 构型2 构型3 构型4 构型5 构型6 构型7 构型8 构型9 构型10 构型11 构型12 构型13 构型14 构型15 图 1 二维图像边缘点的 16 种构型 在构型 5 和构型 10 中，对边缘点的连接有 2 种不同的方法。这种连接的不确定性称为构型的 二义性。在二维情况下，轮廓的二义性容易解决： 对每个二维情况，取任何一种方法都不会影响最 终结果。 步进算法具体如下： ① 选择一个单元； ② 计算该单元每个顶点的内/外状态； ③ 生成每个顶点二进制状态的编码索引值； ④ 利用编码索引值查构型表得到所需的拓 扑状态； ⑤ 用内插计算构型表中每边的轮廓位置。 上述方法应用于三维图像时，每个象素有 8 个 顶 点 ， 根 据 顶 点 与 灰 度 阈 值 的 关 系 一 共 有 2 8 =256 种构型。三维图像的轮廓是由许多小三角 形面片镶嵌而成的，更为复杂。全部 256 种构型 的信息组成一个“构型—三角剖分”查找表。它 包括 256 个索引项，每个索引项包含索引号以及 指向该种三角剖分中的一个指针。通过查表可以 直接得到轮廓段的拓扑信息、哪一条边与体素相 交、应当使用哪些顶点内插产生交点等。对于每 个体素，根据它的索引号在“构型—三角剖分”查 结果 程序的核心代码如下： 1）初始化 ren = vtkRenderer::New(); renWin = vtkRenderWindow::New(); iren = vtkRenderWindowInteractor::New(); mapper = vtkPolyDataMapper::New(); actor = vtkActor::New(); marchingcubes=vtkImageMarchingCubes::New(); property=vtkProperty::New(); *reader= vtkImageReader:: vtkImageReader New(); *m_vtkExport= vtkImage vtkImageImport *m_vtkImport= vtkImage 2）分割 reader->SetFilePrefix("D:\Head"); //D:\Head 为存 reader->SetDataByteOrderToLittleEndian(); 放人体头部组织 CT 扫描图像的文件夹 m_vtkData= reader->GetOutput(); vtkImageExport Export::New(); Import::New(); m_itkvtkimport= ITKVTKImportType::New(); m_itkvtkExport= ITKVTKExportType::New(); m_vtkExport->SetInput(m_vtkData); ConnectVTKToITK(m_vtkExport, m_itkvtkimport); m_gradfilter= GradfilterType::New(); m_sigfilter= SigfilterType::New(); New(); //确定种子点 NodeType node; m_itkvtkimport->GetOutput()->Update(); m_points= NodeContainer::New(); m_points->Initialize(); m_fastmarchingfilter= FastmarchingType:: 

18 深圳职业技术学院学报 第 6 卷 typedef InternalImageType::IndexType Index for (int i=1; i<2;i++) //添加六个种子点 { Type; IndexType seed; seed[0] = static_cast( 120 ); seed[1] = static_cast( 111 ); seed[2] = static_cast( 79 ); } //设置参数 m_gradfilter->SetSigma(1); m_sigfilter->SetOutputMinimum(0.0); m_sigfilter->SetOutputMaximum(1.0); m_fastmarchingfilter->SetTrialPoints(m_points); //创建分割流水线 m_gradfilter->SetInput(m_itkvtkimport-> GetOutput()); m_sigfilter->SetInput(m_gradfilter->GetO utput()); m_fastmarchingfilter->SetInput(m_sigfilte r->GetOutput()); m_itkvtkExport->SetInput(m_fastmarchin gfilter->GetOutput()); //把 itkdata 转化为 vtkdata ConnectITKToVTK(m_itkvtkExport, m_vtkImport); m_vtkImport->GetOutput()->Update(); vtkImageThreshold *m_threshold = vtk ImageThreshold::New(); m_threshold->SetInput(m_vtkImport->Ge tOutput()); vtkImageMathematics *m_math = vtk ImageMathematics::New(); m_math->SetOperationToMultiply(); m_math->SetInput1(reader->GetOutput()); m_math->SetInput2(m_threshold->GetOutp ut()); 3）三维显示 marchingcubes->SetInput(m_math->GetOut mapper->SetInput( marchingcubes->GetOut put()); put() ); actor->SetMapper( mapper ); actor->SetProperty(property); ren->AddActor(actor); CRect rect; this->GetDlgItem(IDC_RENDER)->GetClie ntRect(&rect); iren->Initialize(); renWin->SetSize(rect.right-rect.left,rect.bott om-rect.top); 首先由 ITK 读取图像数据，然后对图像进行分 割处理，再通过 ConnectITKToVTK 将数据转换为 VTK 支持的数据类型，由 VTK 进行三维显示。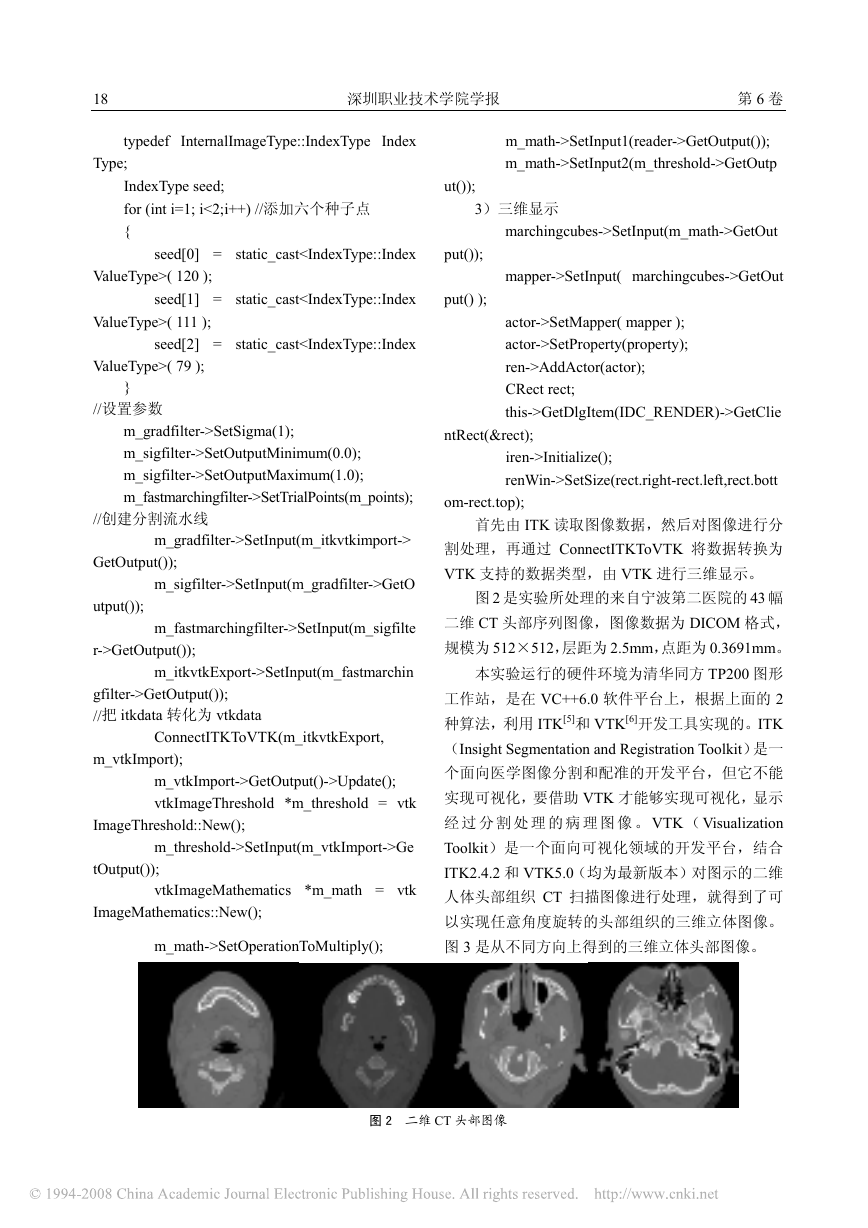 图 2 是实验所处理的来自宁波第二医院的 43 幅 二维 CT 头部序列图像，图像数据为 DICOM 格式， 规模为 512×512，层距为 2.5mm，点距为 0.3691mm。 本实验运行的硬件环境为清华同方 TP200 图形 工作站，是在 VC++6.0 软件平台上，根据上面的 2 种算法，利用 ITK[5]和 VTK[6]开发工具实现的。ITK （Insight Segmentation and Registration Toolkit）是一 个面向医学图像分割和配准的开发平台，但它不能 实现可视化，要借助 VTK 才能够实现可视化，显示 经 过 分 割 处 理 的 病 理 图 像 。VTK （Visualization Toolkit）是一个面向可视化领域的开发平台，结合 ITK2.4.2 和 VTK5.0（均为最新版本）对图示的二维 人体头部组织 CT 扫描图像进行处理，就得到了可 以实现任意角度旋转的头部组织的三维立体图像。 图 3 是从不同方向上得到的三维立体头部图像。 图 2 二维 CT 头部图像 

第 3 期 王京阳，等：基于 ITK 和 VTK 的三维成像实现 19 图 3 三维分割算法得到的不同角度的三维头部图像 4 结 论 ITK在图像读取、分割与配准方面具有较强 的能力，而VTK是实现三维可视化的理想工具， 但由于二者设计与编程风格相差较大，要实现二 者的有机结合，对开发人员来说存在一定难度。 笔者利用VTK与ITK的集成来实现并构成一个医 学图像三维可视化系统，以实例说明了如何利用 ITK来读取DICOM图像序列，转换为VTK支持的 数据类型的方法。并给出了三维重建的结果。实 验证明，VTK与ITK的集成，能充分利用它们在 图像处理与可视化方面的强大功能，是设计医学 图像可视化系统的一种十分理想的方法。 参考文献： [1] 田 捷，包尚联，周明全．医学影像处理和分析 [M]．北京：电子工业出版社，2003． [2] 祁俐娜，罗述谦．基于 VTK 的医学图像三维重建[J]．北 京生物医学工程，2006，25（1）． [3] Sethian J A. Fast marching methods[J]. SIAM Review, 1999，41（2）：199-235． [4] Sethian J A. A fast marching level set method for monotonically advancing fronts[A]//Proceedings of the National Academy of Sciences, Vol 93 ， 1996 ： 1591-1595． [5] Luis Ib´a˜nez, Will Schroeder，Lydia Ng. Josh Cates and the Insight Software Consortium[C]//The ITK Software Guide(Second Edition)Updated for ITK version 2.4. NewYork: Kitware Inc Publisher, 2005． [6] Schroeder W, Martin K, Lorensen B. The Visualization Toolkit: An Object Oriented Approach to 3D Graphics (3rd Edition) [M]. NewYork: Kitware Inc Publisher, 2003． Implementation of 3D Imaging Based on ITK and VTK WANG Jingyang1,2, ZHOU Zhenhuan1, ZHAO Ming1 , WANG Anming1,3 （1. Shenzhen Polytechnic, Shenzhen, Guangdong 518055; 2. Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, Guangdong 518055, 3. Nanchang University, Nanchang, Jiangxi 330031, China） Abstract: The paper introduces the principle of classical fast marching image segmentation and Marching Cubes Visualization algorithms, and integrates ITK with VTK in order to develop medical images by the former and visualize images by the latter. The result indicates that this method can acquire detailed features of pathology part clearly, with its high performance in medical image visualization. Key words: visualization; fast marching; marching cubes （责任编辑：王璐）