2020年吉林长春中考数学真题及答案.doc-资料库

第1页 / 共21页

第2页 / 共21页

第3页 / 共21页

第4页 / 共21页

第5页 / 共21页

第6页 / 共21页

第7页 / 共21页

第8页 / 共21页

2020 年吉林长春中考数学真题及答案一、选择题（本大题共 8 小题，每小题 3 分，共 24 分） 1．（3 分）如图，数轴上被墨水遮盖的数可能为（） A．﹣1 B．﹣1.5 C．﹣3 D．﹣4.2 2．（3 分）为了增加青少年的校外教育活动场所，长春市将建成面积约为 79000 平方米的新少年宫，预计 2020 年 12 月正式投入使用．79000 这个数用科学记数法表示为（） A．79×103 B．7.9×104 C．0.79×105 D．7.9×105 3．（3 分）下列图形是四棱柱的侧面展开图的是（） A． B． C． D． 4．（3 分）不等式 x+2≥3 的解集在数轴上表示正确的是（） A． B． C． D． 5．（3 分）比萨斜塔是意大利的著名建筑，其示意图如图所示，设塔项中心点为点 B，塔身中心线 AB与垂直中心线 AC的夹角为∠A，过点 B向垂直中心线 AC引垂线，垂足为点 D．通过测量可得 AB、BD、AD的长度，利用测量所得的数据计算∠A的三角函数值，进而可求 ∠A的大小．下列关系式正确的是（）

A．sinA＝ B．cosA＝ C．tanA＝ D．sinA＝ 6．（3 分）如图，AB是⊙O的直径，点 C、D在⊙O上，∠BDC＝20°，则∠AOC的大小为（） A．40° B．140° C．160° D．170° 7．（3 分）如图，在△ABC中，∠BAC＝90°，AB＞AC．按下列步骤作图： ①分别以点 B和点 C为圆心，大于 BC一半的长为半径作圆弧，两弧相交于点 M和点 N； ②作直线 MN，与边 AB相交于点 D，连结 CD．下列说法不一定正确的是（） A．∠BDN＝∠CDN B．∠ADC＝2∠B

C．∠ACD＝∠DCB D．2∠B+∠ACD＝90° 8．（3 分）如图，在平面直角坐标系中，点 A的坐标为（3，2），AB⊥x轴于点 B，点 C是线段 OB上的点，连结 AC．点 P在线段 AC上，且 AP＝2PC，函数 y＝（x＞0）的图象经过点 P．当点 C在线段 OB上运动时，k的取值范围是（） A．0＜k≤2 B． ≤k≤3 C． ≤k≤2 D． ≤k≤4 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 9．（3 分）长春市净月潭国家森林公园门票的价格为成人票每张 30 元，儿童票每张 15 元．若购买 m张成人票和 n张儿童票，则共需花费元． 10．（3 分）分解因式：a2﹣4＝． 11．（3 分）若关于 x的一元二次方程 x2﹣2x+m＝0 有两个相等的实数根，则实数 m的值为． 12．（3 分）正五边形的一个外角的大小为度． 13．（3 分）如图，在△ABC中，∠ABC＝90°，AB＝BC＝2，以点 C为圆心，线段 CA的长为半径作，交 CB的延长线于点 D，则阴影部分的面积为（结果保留π）． 14．（3 分）如图，在平面直角坐标系中，点 A的坐标为（0，2），点 B的坐标为（4，2）．若抛物线 y＝﹣ （x﹣h）2+k（h、k为常数）与线段 AB交于 C、D两点，且 CD＝ AB，则 k的值为．

三、解答题（本大题共 10 小题，共 78 分） 15．（6 分）先化简，再求值：（a﹣3）2+2（3a﹣1），其中 a＝． 16．（6 分）现有三张不透明的卡片，其中两张卡片的正面图案为“神舟首飞”，第三张卡片的正面图案为“保卫和平”，卡片除正面图案不同外，其余均相同．将这三张卡片背面向上洗匀，从中随机抽取一张，记录图案后放回，重新洗匀后再从中随机抽取一张．请用画树状图（或列表）的方法，求两次抽出的卡片上的图案都是“保卫和平”的概率．（图案为“神舟首飞”的两张卡片分别记为 A1、A2，图案为“保卫和平”的卡片记为 B） 17．（6 分）图①、图②、图③均是 3×3 的正方形网格，每个小正方形的边长为 1，每个小正方形的顶点称为格点，线段 AB的端点均在格点上，只用无刻度的直尺，在给定的网格中，按下列要求以 AB为边画△ABC．要求：（1）在图①中画一个钝角三角形，在图②中画一个直角三角形，在图③中画一个锐角三角形；（2）三个图中所画的三角形的面积均不相等；（3）点 C在格点上． 18．（7 分）在国家精准扶贫的政策下，某村企生产的黑木耳获得了国家绿色食品标准认证，

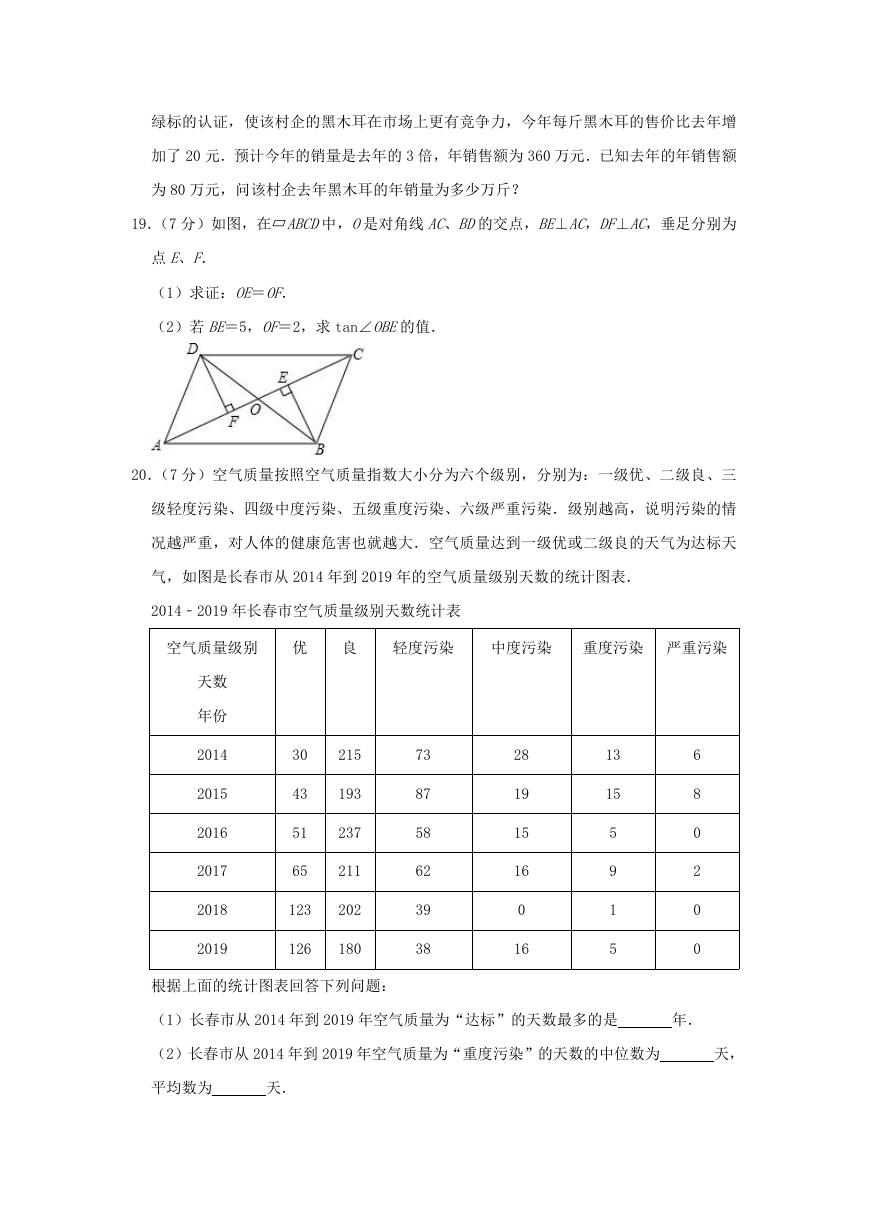
绿标的认证，使该村企的黑木耳在市场上更有竞争力，今年每斤黑木耳的售价比去年增加了 20 元．预计今年的销量是去年的 3 倍，年销售额为 360 万元．已知去年的年销售额为 80 万元，问该村企去年黑木耳的年销量为多少万斤？ 19．（7 分）如图，在▱ABCD中，O是对角线 AC、BD的交点，BE⊥AC，DF⊥AC，垂足分别为点 E、F．（1）求证：OE＝OF．（2）若 BE＝5，OF＝2，求 tan∠OBE的值． 20．（7 分）空气质量按照空气质量指数大小分为六个级别，分别为：一级优、二级良、三级轻度污染、四级中度污染、五级重度污染、六级严重污染．级别越高，说明污染的情况越严重，对人体的健康危害也就越大．空气质量达到一级优或二级良的天气为达标天气，如图是长春市从 2014 年到 2019 年的空气质量级别天数的统计图表． 2014﹣2019 年长春市空气质量级别天数统计表空气质量级别优良轻度污染中度污染重度污染严重污染天数年份 2014 2015 2016 2017 2018 2019 30 43 51 65 215 193 237 211 123 202 126 180 73 87 58 62 39 38 28 19 15 16 0 16 13 15 5 9 1 5 6 8 0 2 0 0 根据上面的统计图表回答下列问题：（1）长春市从 2014 年到 2019 年空气质量为“达标”的天数最多的是年．（2）长春市从 2014 年到 2019 年空气质量为“重度污染”的天数的中位数为天，平均数为天．

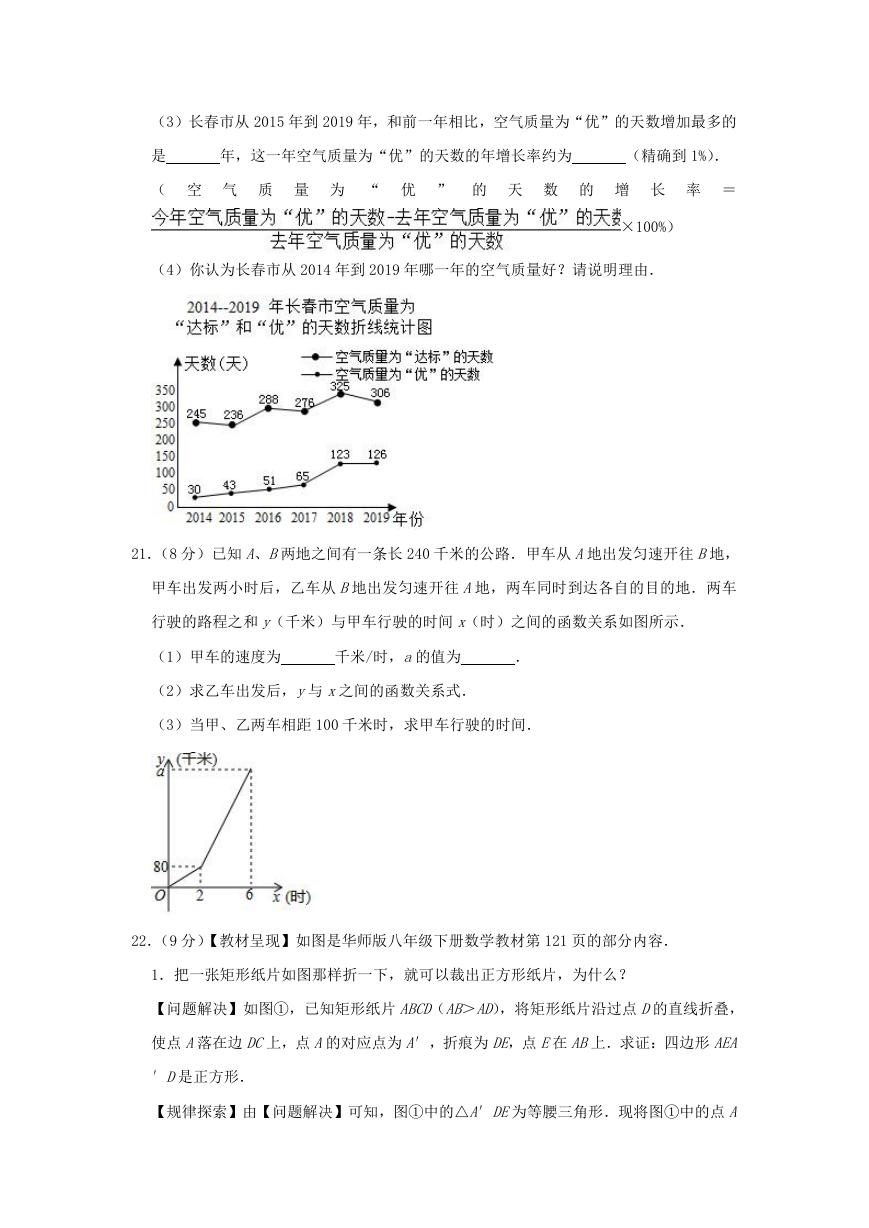
（3）长春市从 2015 年到 2019 年，和前一年相比，空气质量为“优”的天数增加最多的是年，这一年空气质量为“优”的天数的年增长率约为（精确到 1%）．（空气质量为 “ 优 ” 的天数的增长率＝ ×100%）（4）你认为长春市从 2014 年到 2019 年哪一年的空气质量好？请说明理由． 21．（8 分）已知 A、B两地之间有一条长 240 千米的公路．甲车从 A地出发匀速开往 B地，甲车出发两小时后，乙车从 B地出发匀速开往 A地，两车同时到达各自的目的地．两车行驶的路程之和 y（千米）与甲车行驶的时间 x（时）之间的函数关系如图所示．（1）甲车的速度为千米/时，a的值为．（2）求乙车出发后，y与 x之间的函数关系式．（3）当甲、乙两车相距 100 千米时，求甲车行驶的时间． 22．（9 分）【教材呈现】如图是华师版八年级下册数学教材第 121 页的部分内容． 1．把一张矩形纸片如图那样折一下，就可以裁出正方形纸片，为什么？【问题解决】如图①，已知矩形纸片 ABCD（AB＞AD），将矩形纸片沿过点 D的直线折叠，使点 A落在边 DC上，点 A的对应点为 A′，折痕为 DE，点 E在 AB上．求证：四边形 AEA ′D是正方形．【规律探索】由【问题解决】可知，图①中的△A′DE为等腰三角形．现将图①中的点 A

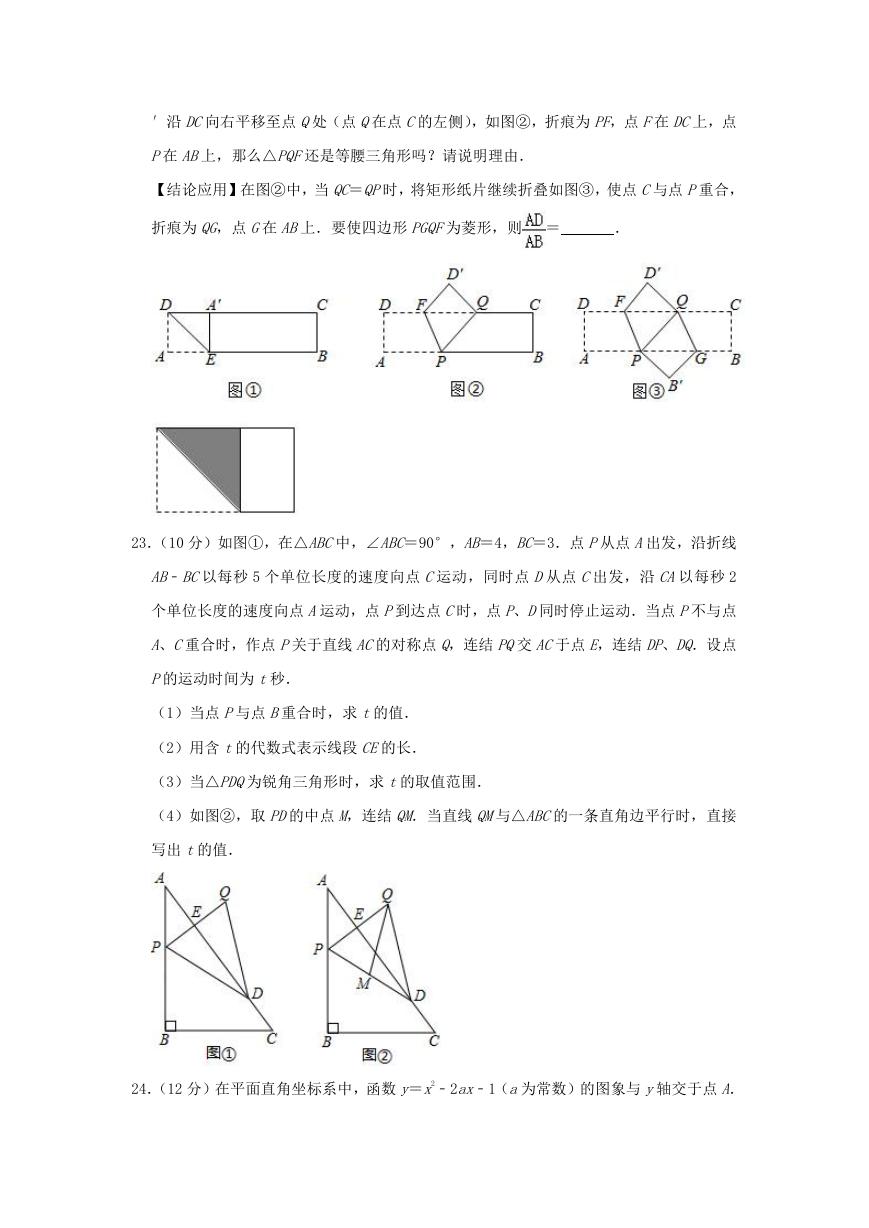
′沿 DC向右平移至点 Q处（点 Q在点 C的左侧），如图②，折痕为 PF，点 F在 DC上，点 P在 AB上，那么△PQF还是等腰三角形吗？请说明理由．【结论应用】在图②中，当 QC＝QP时，将矩形纸片继续折叠如图③，使点 C与点 P重合，折痕为 QG，点 G在 AB上．要使四边形 PGQF为菱形，则＝． 23．（10 分）如图①，在△ABC中，∠ABC＝90°，AB＝4，BC＝3．点 P从点 A出发，沿折线 AB﹣BC以每秒 5 个单位长度的速度向点 C运动，同时点 D从点 C出发，沿 CA以每秒 2 个单位长度的速度向点 A运动，点 P到达点 C时，点 P、D同时停止运动．当点 P不与点 A、C重合时，作点 P关于直线 AC的对称点 Q，连结 PQ交 AC于点 E，连结 DP、DQ．设点 P的运动时间为 t秒．（1）当点 P与点 B重合时，求 t的值．（2）用含 t的代数式表示线段 CE的长．（3）当△PDQ为锐角三角形时，求 t的取值范围．（4）如图②，取 PD的中点 M，连结 QM．当直线 QM与△ABC的一条直角边平行时，直接写出 t的值． 24．（12 分）在平面直角坐标系中，函数 y＝x2﹣2ax﹣1（a为常数）的图象与 y轴交于点 A．

（1）求点 A的坐标．（2）当此函数图象经过点（1，2）时，求此函数的表达式，并写出函数值 y随 x的增大而增大时 x的取值范围．（3）当 x≤0 时，若函数 y＝x2﹣2ax﹣1（a为常数）的图象的最低点到直线 y＝2a的距离为 2，求 a的值．（4）设 a＜0，Rt△EFG三个顶点的坐标分别为 E（﹣1，﹣1）、F（﹣1，a﹣1）、G（0，a ﹣1）．当函数 y＝x2﹣2ax﹣1（a为常数）的图象与△EFG的直角边有交点时，交点记为点 P．过点 P作 y轴的垂线，与此函数图象的另一个交点为 P′（P′与 P不重合），过点 A作 y轴的垂线，与此函数图象的另一个交点为 A′．若 AA′＝2PP′，直接写出 a的值．

资料库

2020年吉林长春中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料