第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
数字逻辑实用教程（王玉龙）答案.doc
第二章作业及参考答案
第二章作业及参考答案
1．设 A、B、C 为逻辑变量，试回答
（1）若已知 A+B=A+C，则 B=C，对吗？
（2）若已知 AB=AC，则 B=C，对吗？
（3）若已知
CABA
AB
AC
，则 B=C，对吗？
答：（1）不对。∵ A=1，B=1，C=0 时有 A+B=A+C，但此时 B≠C。
（2）不对。∵ A=0，B=1，C=0 时有 AB=AC，但此时 B≠C。
（3）对。∵ A=0 满足 AB=AC，A=0 代入 A+B=A+C，得 B=C；A=1 满足 A+B=A+C，代
入 AB=AC，得 B=C。∴ 无论 A 取值如何，都有 B=C。
2．试用逻辑代数的基本公式，化简下列逻辑函数：
（1）
)CBA)(CBA(
与对或的分配律
CCBBACB
与对或的分配律
)A
BC(AB
互补律
（2）
答：（1）
)CBA)(CBA(
)CBA(CB)CBA(A
BAA
AC
（2）
BC(AB
ABC
AB
吸收律
BC
AB
重叠律
AC
CB
)A
AB
AAB
与对或的分配律
3．已知下面的电灯线路，a、b、c、d、e 为开关，F2 为电灯。若假定开关状态为逻辑变量，
电灯状态为逻辑函数，试写出电灯状态的函数表达式。
答：设 a=1 对应开关 a 闭合，其他开关同；F2=1
对应电灯亮。则
F2
decab
a
d
c
b
e
F2
220V
5．将下列逻辑函数展开为最小项表达式。
（1）
F(A,
C)B,
答：
BCACBA
C)B,
BCACBA
(A)C
)7,6,5,4,3,1(
F(A,
)(CB
A(B
ABC
BCACBACBACBACBACAB
7．将下列逻辑函数展开为最大项表达式。
BCACB)A
（1）
F(A,
B)(BA(C)B,
C)
答：
F(A,
9．已知函数的真值表如下，列出该函数的最小项及最大项表达式。
B)(BA(C)B,
BAA)(CCBA(
BA)(CBA()CBA)(CBA(
(0,1,2,6)
C)
C)
C)
真值表
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
F
0
0
0
1
0
1
1
1
答：最小项表达式为：
F = m3+m5+m6+m7 = ∑(3,5,6,7)
∴
mmmmF
2
1
0
4
∴ 可按下面求得最大项表达式。
4
2
0
1
mmmm
4
MMMM
mmmmFF
0
)4,2,1,0(
4
2
1
2
1
0
12．试用德·摩根定理及香农定理分别求下列函数的反函数。
（2）Z = ∑(4,5,6,7)
（3）Z = ∏(0,2,4,6)
（4）
]G)FEDC(B[AZ
6
7
4
mmmm)7,6,5,4(
答：（2）
Z
MMMMmmmmmmmmZ
（3）
Z
mmmmMMMMMMMMZ
MMMM6),4,2,0(
5
4
6
4
6
4
5
0
2
6
7
7
5
6
5
7
4
4
6
2
0
2
4
6
0
2
4
0
（4）
)7,6,5,4(
6
)6,4,2,0(
]G)FEDC(B[AZ
]G)FE)(DC[(BAZ
13．试用对偶定理（或对偶规则）求下列函数的对偶式。
（1）
（2）
C)(CA)(BA(Z
F)DE
ABDDCBAZ
答：（1）对函数的变量取反，然后求函数的反函数，则得到函数的对偶函数。∴
F)EDC)(CA)(BA(Z'
也即
AB[Z'
F)]ED(CCA
（2）
BADDCBABADDCBAZ'
16．试用展开定理将下列函数展开为最小项表达式和最大项表达式。
)CB(A)C,B,A(F
（2）
答：
)BA
CBACAB
)7,6,5,4,1(
(AB
CBABA
CBACBA
AB(C)BABA
)C,B,0(FA)C,B,1(FAF
CBA1A
CBAA
)CAA(B)0A(B
AB
C
ABC
)]C,B,0(FA[F
)1A)(CBA(
C)BA(
(A
)(AB
)]CA)(0A(B[
BC)[
A(A
AB(
AB(
)ABC)(
(AC[
B
)]ABB)(
(AC[
C)(A
BA(
)32,0(
，
)]AB0)(
C)
)]C,B,1(FA[
)]CA)(1A(B[
)]C
)]AB1)(
BA(C[
)ABC(
)CBA)(CB
19．证明下列有关“异或”运算的公式。
（1）
ABA
⊙
1BAB
（3）
(A
答：（1）
AC)B
(B
C)
BABABA
AB
ABA
⊙ B
A(
BABABA1BA1B)
AB
ABA
⊙ B
CBABACB)ABA(C)B
1BA
（3）
(A
ABC
CBACBA
CBA
CB(A
C)BCB(A)BC
C)BCB(ACBCBA
A
C)BC(B
CBA
22．求下列函数的最大项表达式，及反函数和对偶函数的最小项表达式和最大项表达式。
（1）F(A,B,C) = ∑(0,1,2,5,7)
答：最大项表达式为 F = ∏(3,4,6)
反函数的最小项表达式为
F
)6,4,(3
，最大项表达式为
F
)7,5,2,1,0(
对偶函数的最小项表达式为
'F
)
(4,3,1
，最大项表达式为
'F
)0,2,5,6,7(
23．用代数法将下列函数化简为最简“与或”表达式。
（2）
CBACBACBACBAF
答：
CBACBACBACBAF
C(BA
AC(B)AA(CBC)
CBCBBA
C(BBA
C)
BBA
B
A)
24. 用代数法将下列函数化简为最简“或与”表达式。
)DCB)(DCA)(BA(F
（1）
答：
F'
AB
)''F(F
AB
AB
AB
DCBDCA
D)CBA(
DCAB
DC
)DC)(BA(
25．试用卡诺图化简下列函数为最简积之和式。
（2）F(A,B,C,D) = ∑(2,3,6,7,8,10,12,14)
答：卡诺图如下，
AB
CD
00
01
11
10
00 01 11 10
2
3
7
6
14
10
12
8
DACAF
26. 试用卡诺图化简下列函数为最简和之积式。
（2）F(A,B,C,D)= ∑(0,2,5,7,8,10,13,15)
（3）F(A,B,C,D,E)= ∑(0,2,8,10,12,14,18,26,30)
答：（2）F=∏(1,3,4,6,9,11,12,14)，表示最大项的卡诺图如下，
CD
AB
00 01 11 10
00
01
11
10
4
12
1
3
9
11
6
14
B)(DB(F
D)
（3）F=∏(1,3～7,9,11,13,15,16,17,19～25,27～29,31)，表示最大项的卡诺图如下，
)CB)(DA(EF
A B C
0
0
1
1
1
0
D E
00 01 11 10
0
1
1
0
0
1
1
0
1
5
13
9
25
29
21
17
3
7
15
11
27
31
23
19
4
24
28
20
16
6
22
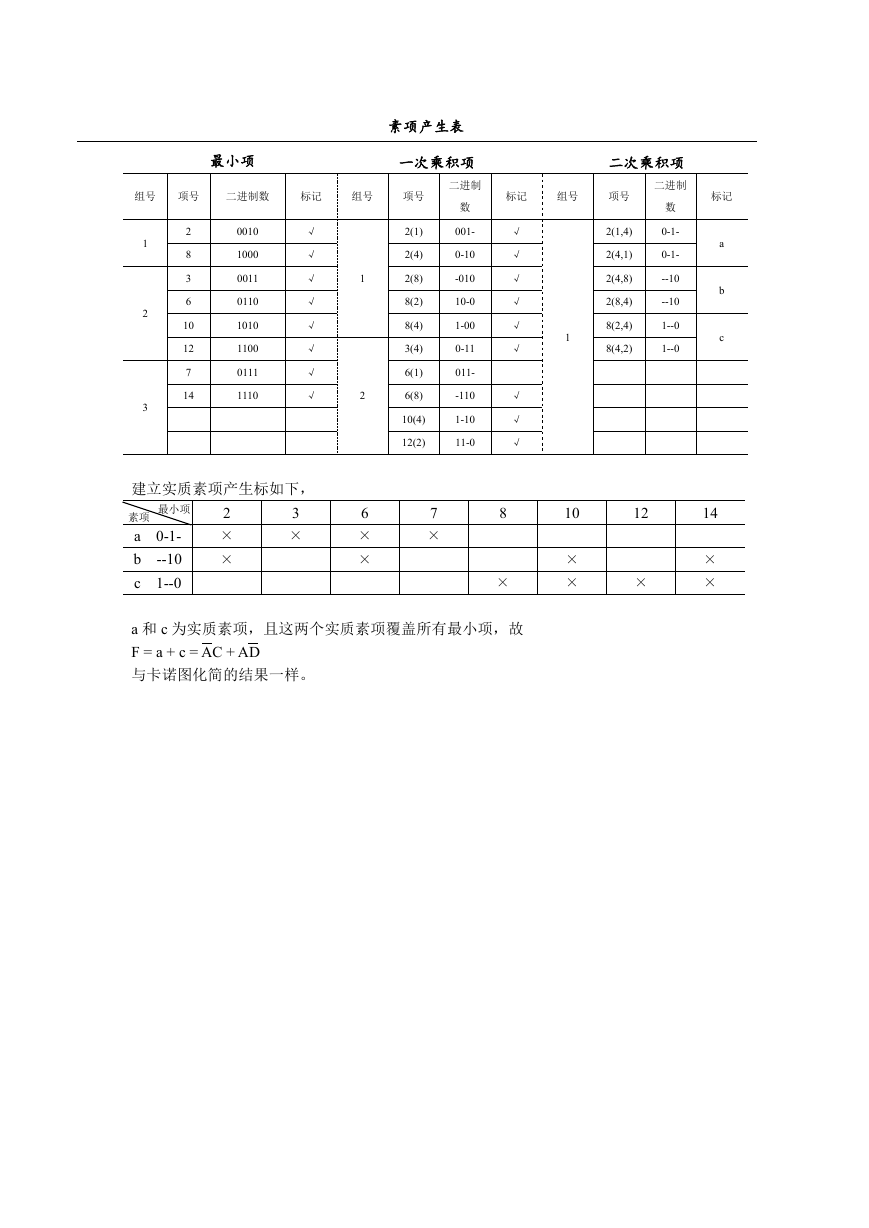
28．试用奎因-麦克拉斯基法化简 25 题（2），并与用卡诺图化简的结果做比较。
答：建立素项产生标，如下。
最小项
素项产生表
一次乘积项
二进制
二次乘积项
二进制
组号 项号
二进制数
标记
组号
项号
标记
组号
项号
标记
2
8
3
6
10
12
7
14
1
2
3
0010
1000
0011
0110
1010
1100
0111
1110
√
√
√
√
√
√
√
√
建立实质素项产生标如下，
素项
a
b
c
最小项
0-1-
--10
1--0
2
×
×
3
×
数
001-
0-10
-010
10-0
1-00
0-11
011-
-110
1-10
11-0
2(1)
2(4)
2(8)
8(2)
8(4)
3(4)
6(1)
6(8)
10(4)
12(2)
√
√
√
√
√
√
√
√
√
7
×
8
×
1
2
6
×
×
1
10
×
×
数
0-1-
0-1-
--10
--10
1--0
1--0
2(1,4)
2(4,1)
2(4,8)
2(8,4)
8(2,4)
8(4,2)
a
b
c
12
×
14
×
×
a 和 c 为实质素项，且这两个实质素项覆盖所有最小项，故
F = a + c = AC + AD
与卡诺图化简的结果一样。
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
