logo资料库

matlab设计2DPSK信号调制与解调..doc

发布时间：2022-05-31 发布人：admin 分类：说明书 资料大小：0.88M 资料格式：doc 举报 版权申诉
第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
资料共11页，剩余部分请下载后查看
    2DPSK 调制与解调系统的仿真 1、 2DPSK 基本原理 1.1 2DPSK 信号原理 2DPSK 方式即是利用前后相邻码元的相对相位值去表示数字信息的一种方式。现假设用Φ表示 本码元初相与前一码元初相之差，并规定：Φ＝0 表示 0 码，Φ＝π表示 1 码。则数字信息序列与 2DPSK 信号的码元相位关系可举例表示如 2PSK 信号是用载波的不同相位直接去表示相应的数字信 号而得出的，在接收端只能采用相干解调，它的时域波形图如图 2.1 所示。 图 1.1 2DPSK 信号 在这种绝对移相方式中，发送端是采用某一个相位作为基准，所以在系统接收端也必须采用相 同的基准相位。如果基准相位发生变化，则在接收端回复的信号将与发送的数字信息完全相反。所 以在实际过程中一般不采用绝对移相方式，而采用相对移相方式。 定义 为本码元初相与前一码元初相之差，假设： →数字信息“0”； →数字信息“1”。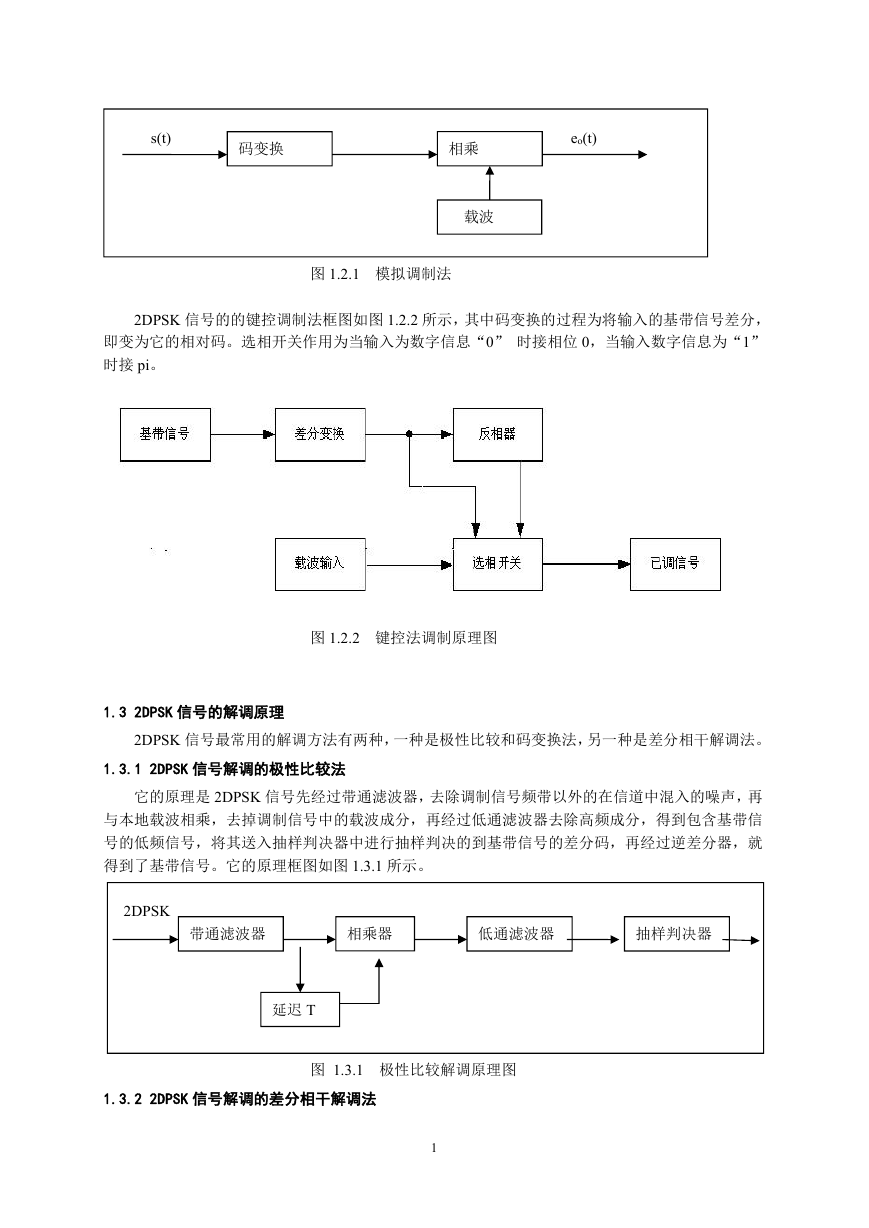 则数字信息序列与 2DPSK 信号的码元相位关系可举例表示如下： 数字信息： 1 0 1 1 0 1 1 1 0 1 DPSK 信号相位： 或：0  1.2 2DPSK 信号的调制原理 一般来说，2DPSK 信号有两种调试方法，即模拟调制法和键控法。2DPSK 信号的的模拟调制 法框图如图 1.2.1 所示，其中码变换的过程为将输入的单极性不归零码转换为双极性不归零码。
    s(t) 码变换 相乘 eo(t) 载波 图 1.2.1 模拟调制法 2DPSK 信号的的键控调制法框图如图 1.2.2 所示，其中码变换的过程为将输入的基带信号差分， 即变为它的相对码。选相开关作用为当输入为数字信息“0” 时接相位 0，当输入数字信息为“1” 时接 pi。 图 1.2.2 键控法调制原理图 1.3 2DPSK 信号的解调原理 2DPSK 信号最常用的解调方法有两种，一种是极性比较和码变换法，另一种是差分相干解调法。 1.3.1 2DPSK 信号解调的极性比较法 它的原理是 2DPSK 信号先经过带通滤波器，去除调制信号频带以外的在信道中混入的噪声，再 与本地载波相乘，去掉调制信号中的载波成分，再经过低通滤波器去除高频成分，得到包含基带信 号的低频信号，将其送入抽样判决器中进行抽样判决的到基带信号的差分码，再经过逆差分器，就 得到了基带信号。它的原理框图如图 1.3.1 所示。 2DPSK 带通滤波器 相乘器 低通滤波器 抽样判决器 延迟 T 1.3.2 2DPSK 信号解调的差分相干解调法 图 1.3.1 极性比较解调原理图 1
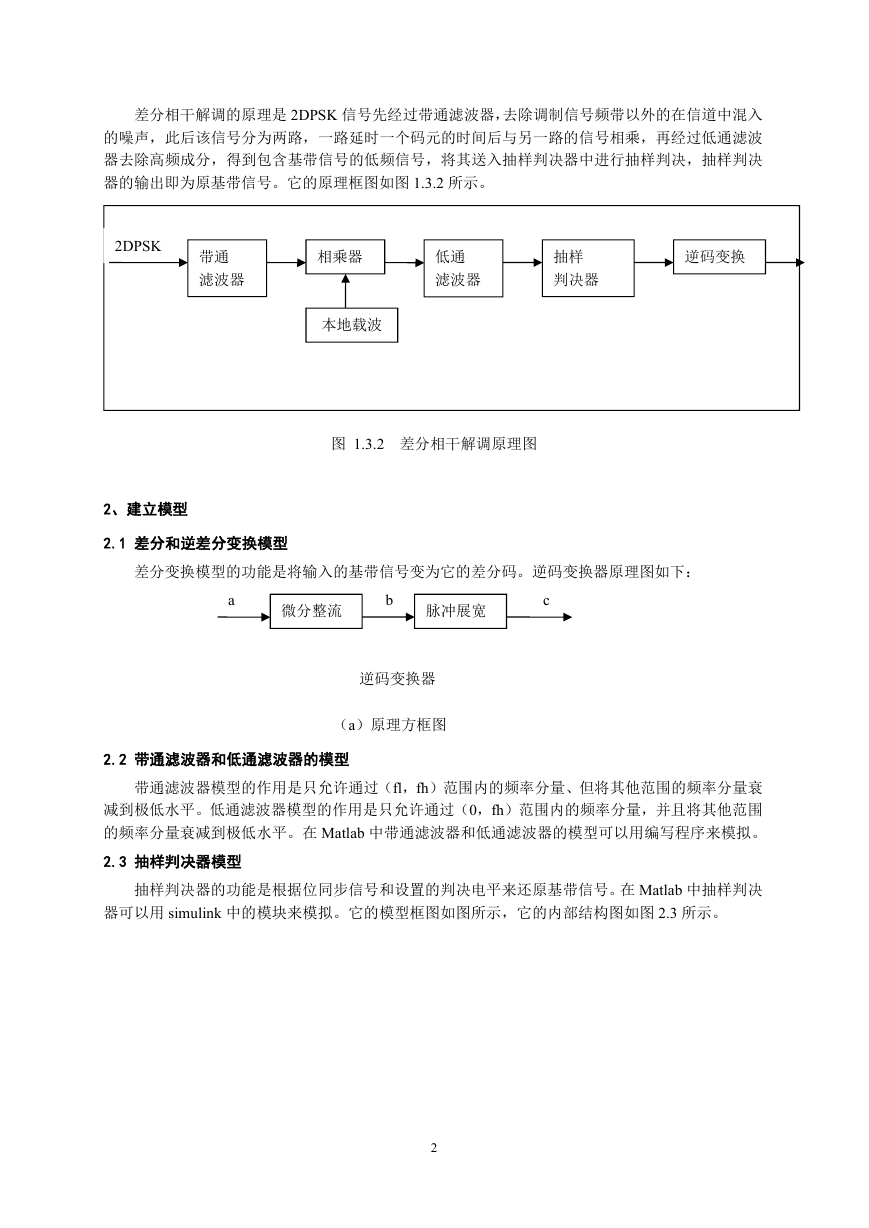
    差分相干解调的原理是 2DPSK 信号先经过带通滤波器，去除调制信号频带以外的在信道中混入 的噪声，此后该信号分为两路，一路延时一个码元的时间后与另一路的信号相乘，再经过低通滤波 器去除高频成分，得到包含基带信号的低频信号，将其送入抽样判决器中进行抽样判决，抽样判决 器的输出即为原基带信号。它的原理框图如图 1.3.2 所示。 2DPSK 带通 滤波器 相乘器 低通 滤波器 抽样 判决器 逆码变换 本地载波 图 1.3.2 差分相干解调原理图 2、建立模型 2.1 差分和逆差分变换模型 差分变换模型的功能是将输入的基带信号变为它的差分码。逆码变换器原理图如下： a 微分整流 b 脉冲展宽 c 逆码变换器 （a）原理方框图 2.2 带通滤波器和低通滤波器的模型 带通滤波器模型的作用是只允许通过（fl，fh）范围内的频率分量、但将其他范围的频率分量衰 减到极低水平。低通滤波器模型的作用是只允许通过（0，fh）范围内的频率分量，并且将其他范围 的频率分量衰减到极低水平。在 Matlab 中带通滤波器和低通滤波器的模型可以用编写程序来模拟。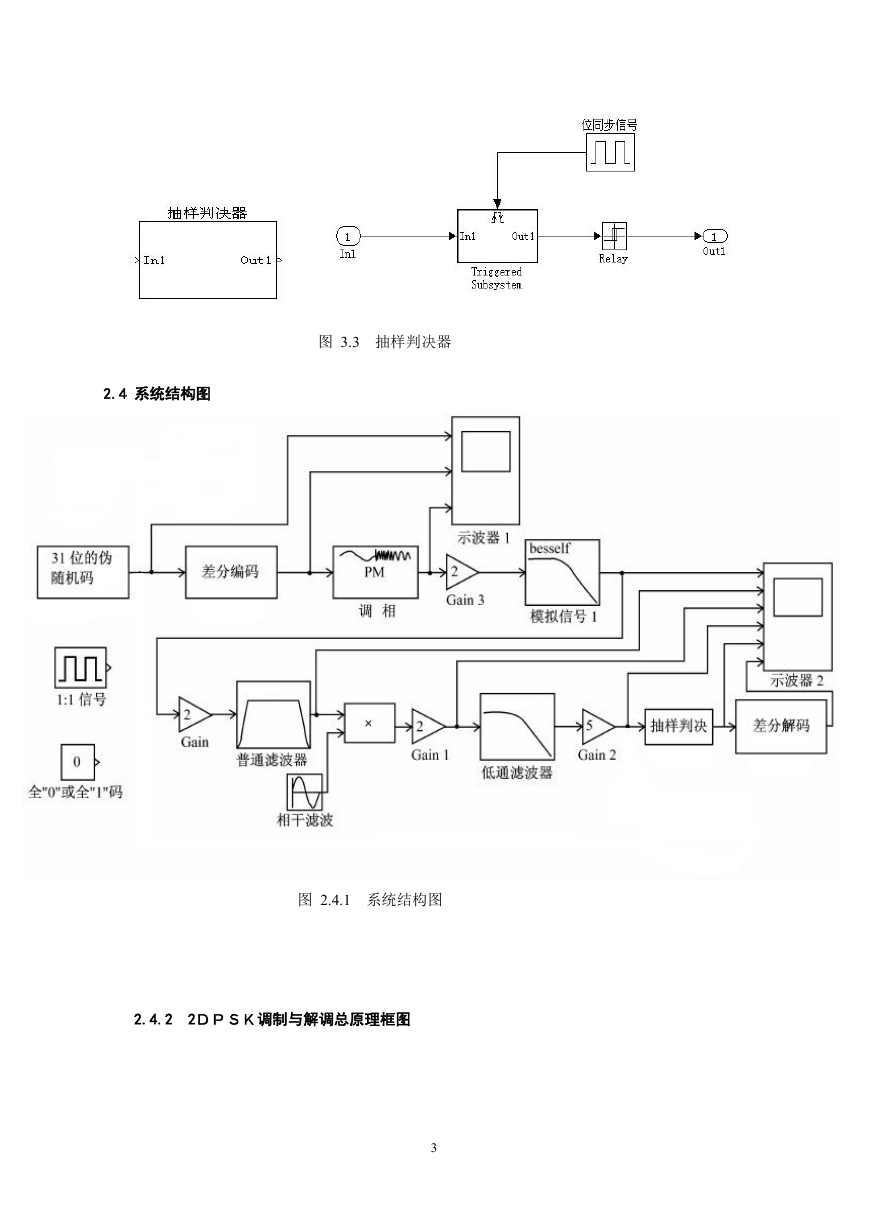 2.3 抽样判决器模型 抽样判决器的功能是根据位同步信号和设置的判决电平来还原基带信号。在 Matlab 中抽样判决 器可以用 simulink 中的模块来模拟。它的模型框图如图所示，它的内部结构图如图 2.3 所示。 2
    图 3.3 抽样判决器 2.4 系统结构图 图 2.4.1 系统结构图 2.4.2 2ＤＰＳＫ调制与解调总原理框图 3
    图 2.4.2 2ＤＰＳＫ调制与解调总原理框图 3、仿真 3.1 仿真程序 %- 2DPSK 调制与解调 %--------------------------------------------------- %>>>>>>>>>>>>>>>>>>Initial_Part>>>>>>>>>>>>>>>>>>>>> %--------------------------------------------------- function y=dpsk2() fs = 30000; Time_Hold_On = 0.1; Num_Unit = fs * Time_Hold_On; High_Level = ones ( 1, Num_Unit ); Low_Level = zeros ( 1, Num_Unit ); w = 300; A = 1; %--------------------------------------------------- %>>>>>>>>>>>>>>>>>>Initial_The_Signal>>>>>>>>>>>>>>> %--------------------------------------------------- Sign_Set = [0,1,1,0,1,0,0,1] Lenth_Of_Sign = length ( Sign_Set ); st = zeros ( 1, Num_Unit * Lenth_Of_Sign ); sign_orign = zeros ( 1, Num_Unit * Lenth_Of_Sign ); sign_result = zeros ( 1, Num_Unit * Lenth_Of_Sign ); t = 0 : 1/fs : Time_Hold_On * Lenth_Of_Sign - 1/fs; %--------------------------------------------------- %>>>>>>>>>>>Generate_The_Original_Signal>>>>>>>>>>>> %--------------------------------------------------- for I = 1 : Lenth_Of_Sign if Sign_Set(I) == 1 4
    sign_orign( (I-1)*Num_Unit + 1 : I*Num_Unit) = High_Level; sign_orign( (I-1)*Num_Unit + 1 : I*Num_Unit) = Low_Level; else end end %--------------------------------------------------- %>>>>>>>>>>>>>>>>>>Modulation_Part>>>>>>>>>>>>>>>>>> %--------------------------------------------------- for I = 1 : Lenth_Of_Sign if Sign_Set(I) == 1 st( (I-1)*Num_Unit + 1 : I*Num_Unit) = A * cos ( 2 * pi * w * t( (I-1)*Num_Unit + 1 : I*Num_Unit ) + ( pi / 2 ) ); else st( (I-1)*Num_Unit + 1 : I*Num_Unit) = A * cos ( 2 * pi * w * t( (I-1)*Num_Unit + 1 : I*Num_Unit ) ); end end 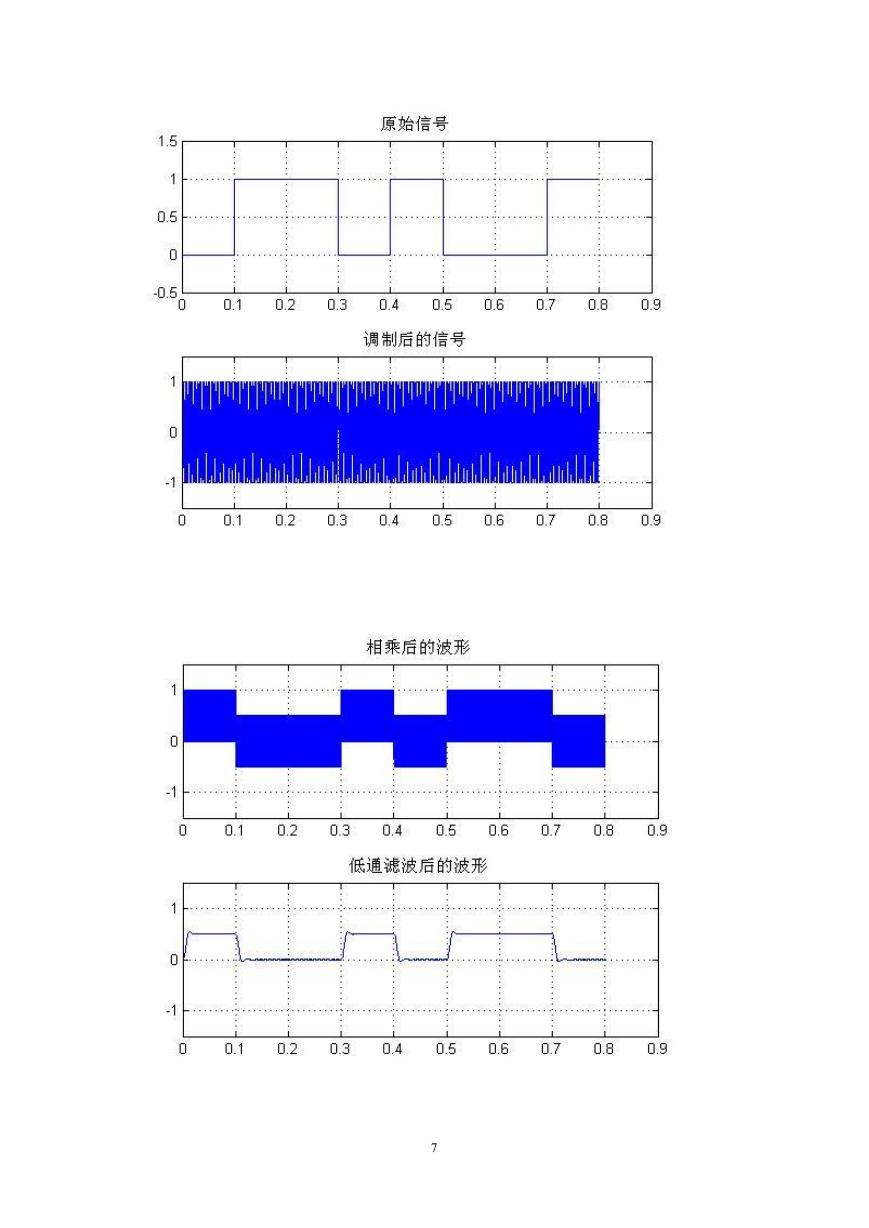figure subplot ( 2, 1, 1 ) plot(t, sign_orign); axis( [ 0 , Time_Hold_On *( Lenth_Of_Sign + 1), - (A / 2), A + (A / 2) ] ); title ( '原始信号' ); grid subplot ( 2, 1, 2 ); plot ( t, st ); axis( [ 0 , Time_Hold_On *( Lenth_Of_Sign + 1), - 3*(A / 2), 3*(A / 2) ] ); title ( '调制后的信号' ); grid %--------------------------------------------------- %>>>>>>>>>>>>>>>>>>相乘>>>>>>>>>>>>>>>>>>>>>>>>>>>>> %--------------------------------------------------- dt = st .* cos ( 2 * pi * w * t ); figure subplot(2,1,1) plot ( t, dt ); axis( [ 0 , Time_Hold_On *( Lenth_Of_Sign + 1), - 3*(A / 2), 3*(A / 2) ] ); title ( '相乘后的波形' ); grid %--------------------------------------------------- 5
    %>>>>>>>>>>>>>>>>>>>低通滤波部分>>>>>>>>>>>>>>>>>>>> %--------------------------------------------------- [N,Wn] = buttord( 2*pi*50, 2*pi*150,3,25,'s'); %临界频率采用角频率表示 [b,a]=butter(N,Wn,'s'); [bz,az]=impinvar(b,a,fs); %映射为数字的 dt = filter(bz,az,dt); subplot(2,1,2) plot ( t, dt ); axis( [ 0 , Time_Hold_On *( Lenth_Of_Sign + 1), - 3*(A / 2), 3*(A / 2) ] ); title ( '低通滤波后的波形' ); grid %--------------------------------------------------- %>>>>>>>>>>>>>抽样判决 & 逆码变换部分>>>>>>>>>>>>>>> %--------------------------------------------------- for I = 1 : Lenth_Of_Sign if dt((2*I-1)*Num_Unit/2) < 0.25 sign_result( (I-1)*Num_Unit + 1 : I*Num_Unit) = High_Level; else sign_result( (I-1)*Num_Unit + 1 : I*Num_Unit) = Low_Level; end end figure plot ( t, sign_result ); axis( [ 0 , Time_Hold_On *( Lenth_Of_Sign + 1), - 3*(A / 2), 3*(A / 2) ] ); title ( '逆码变换后的波形' ); grid 3.2.1 2DPSK 模拟调制和差分相干解调法仿真图 6
    7
    分享到：
    赞 收藏

    相关推荐

    资料库

    移动开发

    共收录1376份资料，累计14个分类，关注成员有19位，主要包括：IOS,Symbian,webOS,WindowsPhone,小程序,Flash,BlackBerry,bada,JavaME,HTML5,iOS,Android,QT,其它

    热门标签

    IOS Symbian webOS WindowsPhone 小程序 Flash BlackBerry bada JavaME HTML5 iOS Android QT 其它

    最新资料