第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
六个维度上的平滑弦状braneworld.pdf
A smoothed string-like braneworld in six dimensions
Abstract
1 Introduction
2 Smoothed string-like geometry
3 Sources properties
4 Gravity localization
4.1 Massless mode
4.2 Massive modes
4.3 Analog quantum potential
5 Conclusions and perspectives
Acknowledgments
References
Eur. Phys. J. C (2015) 75:127
DOI 10.1140/epjc/s10052-015-3350-8
Regular Article - Theoretical Physics
A smoothed string-like braneworld in six dimensions
J. C. B. Araújoa, J. E. G. Silvab, D. F. S. Verasc, C. A. S. Almeidad
Departamento de Física, Universidade Federal do Ceará, C.P. 6030, Fortaleza, Ceará 60455-760, Brazil
Received: 12 October 2014 / Accepted: 9 March 2015 / Published online: 17 March 2015
© The Author(s) 2015. This article is published with open access at Springerlink.com
Abstract We propose a static and axisymmetric braneworld
in six dimensions as a string-like model extension. For a sub-
tle warp function, this scenario provides near brane correc-
tions. By varying the bulk cosmological constant, we obtain a
source which passes through different phases. The solution is
defined both for the interior and for the exterior of the string
and satisfies all the energy conditions. A smoothed gravita-
tional massless mode is localized on the brane, of which the
core is displaced from the origin. In contrast to the thin-string
model, the massive solutions have a high amplitude near the
brane. Furthermore, by means of an analog quantum poten-
tial analysis, we show that only s-wave gravitational Kaluza–
Klein modes are permissible.
1 Introduction
In the last decade, the extra dimension models turned out
to be a cornerstone of high energy physics [1,2]. In particu-
lar, the Randall–Sundrum (RS) model brought the incredible
idea of infinity extra dimensions through a warped geome-
try [2]. Some authors enhanced the RS model results to six
dimensions. Since the two-dimensional transverse manifold
has its own geometry, it leads to some nonexistent features
in the RS models. Indeed, for an axisymmetric brane, the so-
called string-like defect, the brane tension is related with the
conical deficit angle of the transverse space [3–7]. Further,
the Kaluza–Klein (KK) modes produce a smaller correction
to the Newtonian potential [4]. The gauge bosons can be
trapped to the brane by means of only the gravitational inter-
action [8]. Moreover, it is possible to localize the vector and
spinor fields in the same geometry [9].
a e-mail: julio@fisica.ufc.br
b e-mail: euclides@fisica.ufc.br
c e-mail: franklin@fisica.ufc.br
d e-mail: carlos@fisica.ufc.br
In spite of the aforementioned results, the string-like mod-
els exhibit some issues about their sources. In fact, these
branes can be realized as a stable solution of a gauge and
scalar fields [6,7]. Nonetheless, the solution for the Einstein
field equations for these models are still lacking. Amongst the
string-like models, one which the width of the string vanishes
and it is possible to concern with only the vacuum solution is
the Gherghetta–Shaposhnikov (GS) model [4]. However, the
thin-string-like models do not satisfy the dominant energy
condition [10]. In order to overcome it, some authors solved
numerically the equations for an Abelian vortex in six dimen-
sions which exhibits a smooth geometry and satisfies all the
energy conditions [11]. In the supersymmetric approach, a
realistic and smooth cigar solution was also found by numer-
ical means [12].
Another issue of the thin-string-like models, is that all
the regularity conditions are not satisfied at the origin [10].
However, some authors added a conical behavior near the
origin and studied its consequences [13–16], whereas others
tried to smooth this conical behavior [16–24].
In this article we explore some features of a smooth exten-
sion of the GS model built analytically. Besides, using a
smoothed warp function, the metric satisfies all the regu-
larity conditions. We analyze the geometrical and physical
properties of this model which yields an interior and exterior
string-like solution, allowing near brane corrections to the
GS model. The brane core is displaced from the origin. By
studying the gravitational modes, we find a smoothed local-
ized zero mode peaked around the shifted brane core. By
means of a numerical analysis, we find a smooth near brane
correction to the massive KK modes. Further, the quantum
analog potential possesses an infinite well around the origin
which barrier is strongly dependent on the bulk cosmological
constant value.
This work is organized as follows: in Sect. 2, we review the
main characteristics of the string-like branes and we present
our extension. In Sect. 3, we study the properties of the source
from the Einstein equations. Section 4 is devoted to the study
123
127 Page 2 of 8
Eur. Phys. J. C (2015) 75 :127
of the massless and massive gravitational modes upon the
geometry. Finally, in Sect. 5, some final remarks and per-
spectives are outlined.
2 Smoothed string-like geometry
In this section, we review the main properties of the string-
like branes and propose another complete solution.
Let M3 a 3-brane and M2 a two-dimensional Rieman-
nian manifold. A string-like brane M3 is a Lorentzian man-
ifold with axial symmetry about M2. Defining a gaussian
radial coordinate ρ ∈ [0,∞) and an angular coordinate θ ∈
[0, 2π], a well-known ansatz for a warped six-dimensional
string-like braneworld M6 = M p × M2 is given by [3–8]
ds2 = G AB (x ζ , ρ, θ )dx Adx B
= σ (ρ)ημνdx μdx ν + dρ2 + γ (ρ)dθ 2,
(1)
where σ is the so-called warp function, the x ζ are on-brane
coordinates, (ρ, θ ) are coordinates of the transverse mani-
fold, and γ is an angular factor.
The action for the gravitational field is defined as
M6
1
2κ6
R − + Lm
Sg =
where κ6 = 8π/M 4
6 is the six-dimensional bulk Planck
mass and Lm is the matter Lagrangian for the source of the
geometry. Note that in this convention, the bulk cosmological
constant has dimension [] = L
−6 = M 6.
Consider an axisymmetric ansatz for
6 , M 4
(2)
√−g d6x,
the energy-
(3)
(4)
(5)
(6)
momentum tensor [4,8]:
ν = t0(ρ)δμ
T μ
ν ,
ρ = tρ (ρ),
T ρ
θ = tθ (ρ),
T θ
where
TAB = 2√−g
√−gLm )
∂(
∂g AB
.
gAB = −κ6(gAB + TAB ).
From the action (2), we obtain the Einstein equation
R AB − R
(7)
2
In order to guarantee a smooth 3-brane at ρ = 0, we will
adopt the usual regularity conditions [18,19,22,23],
σ (0) = 1, σ(0) = 0,
γ (0) = 0,
= 1,
γ (0)
(8)
(9)
where the prime stands for the derivative ∂ρ.
123
A special analytical string-like braneworld is the GS
−cρ and γ (ρ) = R2
model for which [4,11]
σ (ρ) = e
(10)
where c ∈ R is a constant of which the dimension is [c] =
−1 and R0 is an arbitrary length scale. It is worthwhile
L
to say that the ansatz (10) satisfies only the first regularity
condition.
σ (ρ),
0
The GS model is constructed from the vacuum Einstein
equation with cosmological constant [4]. Then
R = 3κ6.
The scalar curvature for the ansatz (8) is
R = − 15
2
c2,
which yields the well-known relationship [4,8]
c2 = − 2
5
κ6.
(11)
(12)
(13)
ρ
c
2
e
As a result, the GS model has a geometry of a Ad S6 manifold.
Indeed, performing the change of coordinates
z = z(ρ) = 2
(14)
c
and x4 = x4(θ ) = R0θ, the metric in Eq. (1) can be cast in
the conformal form
ds2 =
dz2 + dx 2
+ dx 2
+ dx 2
+ dx 2
2
− dt 2
,
2
3
4
1
a
z
(15)
where a = 2
c is the so-called Ad S radius. Equation (15) is
the Ads6 metric in the conformal coordinates [25,26]. Since
ρ → ∞ ⇒ z → ∞, then the conformal coordinates show
that the warp factor shrinks the geometry to a point at infinity.
Further, by means of the transformation
w = w(z) = a2
z
2
the metric (15) can be written as
ds2=
+dx 2
+dx 2
+dx 2
−dt 2
w
dw2.
2
(16)
+
,
2
3
4
dx 2
1
a
w
a
(17)
The metric in Eq. (17) is in the so-called Poincaré patch and
it is used in the AdS–CFT correspondence [5,27,28].
In the Poincaré patch, the asymptotic point, also known as
the Ad S horizon, is located at w = 0. The decreasing behav-
ior of the warp factor yields an asymptotic conical behav-
ior. Ponton and Poppitz [5] proposed that it is possible to
smooth out this horizon feature by embedding the GS model
in the AdS–CFT correspondence. However, it is worthwhile
to notice that, since the Ricci scalar is everywhere constant,
the singularity at the horizon is not an essential singularity.
Eur. Phys. J. C (2015) 75 :127
Page 3 of 8 127
The existence of an apparent singularity at the horizon
does not prevent the GS model to be a string-like geometry.
Indeed, as shown by Israel, the general solution for a string-
like geometry is given by the Kasner-like manifold
2a1
=dρ2+
ds2
4
ρ
ξ
dz2+χ 2
2a2
ρ
ξ
2a3
dφ2−
ρ
ξ
dt 2,
3
+ a2
2
1
+ a2
(18)
= 1 and χ , ξ ∈ R
where a1 + a2 + a3 = a2
[29]. The constant χ measures the deficit angle whereas
ξ provides the correct mass dimension for the metric. For
a1 = a3 = 0 and a2 = 1 we obtain the Vilenkin string
[30–32]. On the other hand, for a1 = a3 = 2
3 and a2 = − 1
3
we attain the so-called Melvin solution [33]. Other singular
string-like solutions were found for a global string by Cohen
and Kaplan [34] and Gregory [35] in four dimensions. In
six dimensions, Cohen and Kaplan [6] proposed a string-like
solution whose singularity far from the brane is responsible
for the compactification. Gregory found a string-like brane
without singularity which has the same behavior of the GS
model [7]. Moreover, a smooth braneworld which asymptoti-
cally converges to the GS model was obtained by Giovannini
et al. [11]. In this model, the source is given by a local and
Abelian vortex [11].
The metric factors (10) can be regarded as an exterior solu-
tion of the string-like brane of width . For → 0, the brane
is infinitely thin. An awkward property of the thin-string-like
branes is that they do not satisfy the dominant energy condi-
tion, which turns this model a fairly exotic scenario [10]. In
order to overcome these issues, some authors derived numer-
ically the geometry from an Abelian vortex [11] and in a
supersymmetric approach [12]. Here, we propose an exten-
sion of the thin-string-like solution and we investigate the
modifications on the geometrical and physical properties of
this scenario.
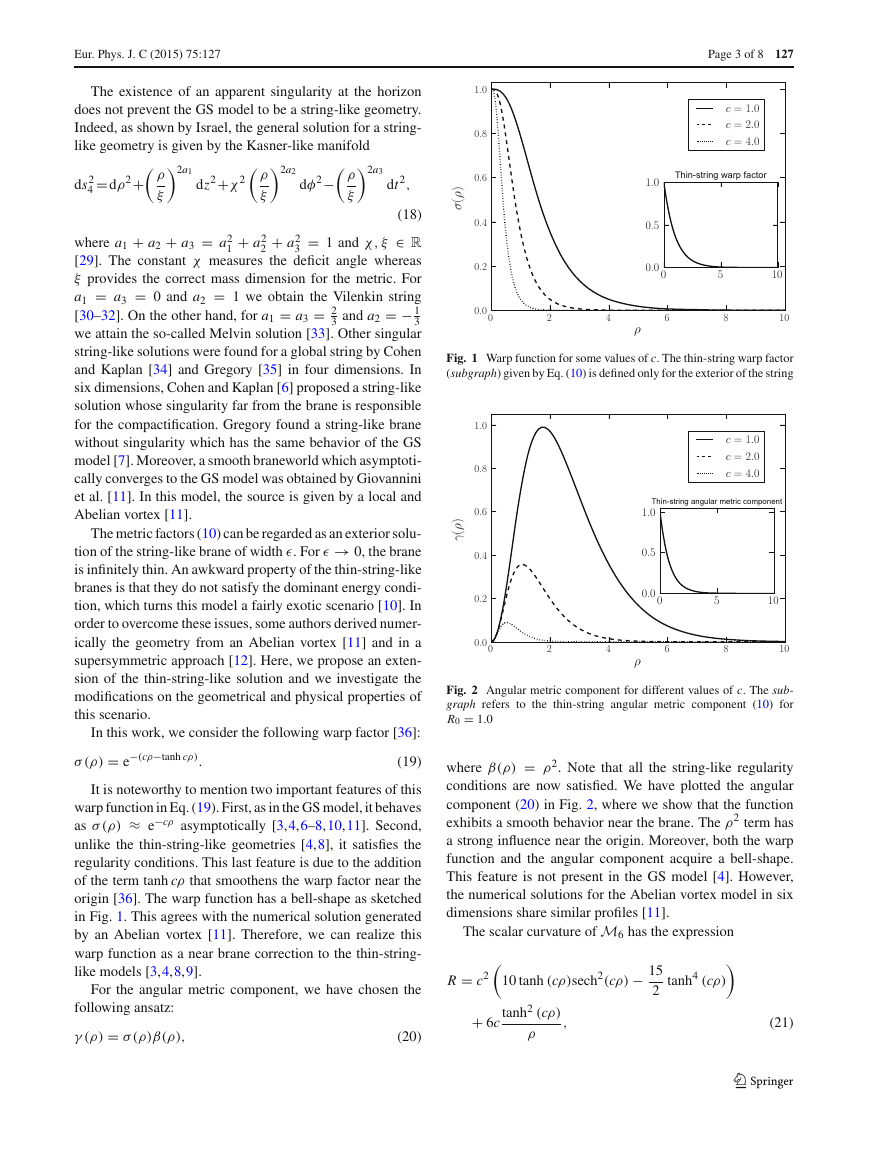
In this work, we consider the following warp factor [36]:
σ (ρ) = e
−(cρ−tanh cρ).
(19)
It is noteworthy to mention two important features of this
warp function in Eq. (19). First, as in the GS model, it behaves
as σ (ρ) ≈ e
−cρ asymptotically [3,4,6–8,10,11]. Second,
unlike the thin-string-like geometries [4,8], it satisfies the
regularity conditions. This last feature is due to the addition
of the term tanh cρ that smoothens the warp factor near the
origin [36]. The warp function has a bell-shape as sketched
in Fig. 1. This agrees with the numerical solution generated
by an Abelian vortex [11]. Therefore, we can realize this
warp function as a near brane correction to the thin-string-
like models [3,4,8,9].
For the angular metric component, we have chosen the
following ansatz:
γ (ρ) = σ (ρ)β(ρ),
(20)
)
ρ
(
σ
1.0
0.8
0.6
0.4
0.2
0.0
0
c
c
c
= 1
= 2
= 4
.0
.0
.0
Thin-string warp factor
5
8
10
10
1.0
0.5
0.0
0
2
4
6
ρ
Fig. 1 Warp function for some values of c. The thin-string warp factor
(subgraph) given by Eq. (10) is defined only for the exterior of the string
)
ρ
(
γ
1.0
0.8
0.6
0.4
0.2
0.0
0
c
c
c
= 1
.0
= 2
.0
= 4.0
Thin-string angular metric component
1.0
0.5
0.0
0
5
10
2
4
ρ
6
8
10
Fig. 2 Angular metric component for different values of c. The sub-
graph refers to the thin-string angular metric component (10) for
R0 = 1.0
where β(ρ) = ρ2. Note that all the string-like regularity
conditions are now satisfied. We have plotted the angular
component (20) in Fig. 2, where we show that the function
exhibits a smooth behavior near the brane. The ρ2 term has
a strong influence near the origin. Moreover, both the warp
function and the angular component acquire a bell-shape.
This feature is not present in the GS model [4]. However,
the numerical solutions for the Abelian vortex model in six
dimensions share similar profiles [11].
The scalar curvature of M6 has the expression
tanh4 (cρ)
10 tanh (cρ)sech2(cρ) − 15
2
tanh2 (cρ)
R = c2
+ 6c
,
ρ
(21)
123
127 Page 4 of 8
Eur. Phys. J. C (2015) 75 :127
c
c
c
.0
= 1
.0
= 2
= 3.0
)
ρ
(
R
60
40
20
0
−20
−40
−60
0
1
2
3
ρ
4
5
6
Fig. 3 Bulk scalar curvature
which behavior is shown in Fig. 3. The curvature is every-
where smooth and asymptotically M6 approaches the Ad S6
case. In fact, considering the change of variable
z = z(ρ) =
2 (ρ)dρ,
ρ
σ− 1
(22)
t0(ρ) +
i
(23)
Using the metric ansatz (1), the Einstein equation (7)
yields the components of the energy-momentum tensor in
the form
tθ (ρ) = 5c2
κ6
tρ (ρ) = 5c2
κ6
t0(ρ) = tθ (ρ) + 5c
2κ6
sech2cρ
sech2cρ + 2
5
tanh2 cρ
1 + 4
5
tanh2 cρ
− sech4cρ
2
− sech4cρ
tanh cρ
, (26)
(27)
(28)
cρ
2
ρ
,
.
For large ρ, the components of the energy-momentum ten-
sor vanish and the vacuum solution of the Einstein equation
yields the relation between c and given by Eq. (13). This
equation determines the bulk to be asymptotically an Ad S6
spacetime. Besides, it also means that, by varying c, we can
study the changes in the source and fields for different bulk
cosmological constant values.
We have plotted in Fig. 4 the components of the energy-
momentum tensor for κ6 = 1. It can be seen that, for i = ρ, θ,
t0(ρ) + ti (ρ) 0,
t0(ρ) 0 (weak energy condition),
ti (ρ) 0 (strong energy condition),
(29)
(30)
(dominant energy condition).
and
t0(ρ) |ti (ρ)|
(31)
Only the c = 1.0 and c = 4.0 cases are presented in Fig. 4.
However, it is straightforward to prove that the conditions
(29)–(31) are satisfied for all the (positive) values of c. Since
the hyperbolic functions in Eqs. (26)–(28) are limited from
0 to 1, all the terms of these equations are positive. Fur-
thermore, the term sech4(cρ) is rather small, what directly
proves the weak and the strong energy conditions. The term
5c
in Eq. (28) is responsible for the proof that the
2κ6
dominant energy condition (31) is satisfied. Firstly, from Eq.
(28), it is obvious that t0(ρ) ≥ tθ (ρ). If we write explicitly
the expressions (26)–(28) in the inequality t0(ρ) ≥ tρ (ρ),
we are led to
sech2(cρ) tanh(cρ) ≥ − 1
10
tanh2(cp)
tanh2(cρ)
(32)
4
5
cρ
cρ
,
which is satisfied, because the left side is always positive.
It is important to note that the near brane corrections, pro-
vided by the ansatz (19) and (20), lead to a displacement
of the core of the source from the origin. Similar results
have been obtained by Giovannini et al. [11] numerically
for higher winding number Abelian vortices and for the
string-cigar model [36]. Moreover, the brane width defined
as ≈ ¯ρ − ρmax, where ¯ρ and ρmax are the positions of the
half-maximum and the maximum of t0, respectively, tends to
= σ (z)
the metric (1) turns into
dz2 + ημνdx μdx ν + β(z)dθ 2
ds2
6
For large ρ, the coordinate z behaves as z ≈ 2
c e c
2
string-cigar metric assumes the form
dz2 + ημνdx μdx ν +
2
≈
ln
z
.
ds2
6
2
c
c
2
Defining the coordinate x4 =
2
changed to
2
2
c ln c
2 z
≈
ds2
6
a
z
a
z
ρ. Then the
2
dθ 2
.
(24)
θ, the metric (24) is
1 −
−dx 2
4
θ
z
− 4θ
z
dz2 + dx 2
1
+ dx 2
3
+ dx 2
2
dz ⊗ dθ − dt 2
.
(25)
Therefore, the metric (25) recovers asymptotically the con-
formal form of the Ad S6 manifold in the Poincaré patch
(15). This ensures us that we may claim that (M6, ds2
) is
an extension of the thin-string models near and far from the
defect.
6
3 Sources properties
In this section, we study the components of the energy-
momentum tensor as well as the value of the cosmological
constant.
123
Eur. Phys. J. C (2015) 75 :127
Page 5 of 8 127
(a)
r
o
s
n
e
t
m
u
t
n
e
m
o
M
-
y
g
r
e
n
E
6
5
4
3
2
1
0
t0
tθ
tρ
(b)
r
o
s
n
e
t
m
u
t
n
e
m
o
M
-
y
g
r
e
n
E
90
80
70
60
50
40
30
20
10
t0
tθ
tρ
0
1
2
3
ρ
4
5
6
0
0
1
2
3
ρ
4
5
6
Fig. 4 Components of the energy-momentum tensor for c = 1.0 (a) and c = 4.0 (b)
zero when c → ∞. Therefore, the GS model can be seen as
a c → ∞-limit of this smoothed version.
4 Gravity localization
We now study the gravity localization on a 3-brane embed-
ded on this six-dimensional geometry. We consider a small
perturbation hμν in the background metric in the form
= σ (ρ, c)(ημν + hμν )dx μdx ν + dρ2 + γ (ρ, c)dθ 2.
ds2
6
(33)
Imposing the transverse traceless gauge ∇ μhμν = 0, the lin-
earization of the Einstein equations yields the equation for
the gravitational perturbation [4,24],
∂A(
√−g6g AB ∂Bhμν ) = 0.
∞
m,l=0
Performing the well-known Kaluza–Klein decomposition [4]
φm,l (ρ)eilθ ,
hμν (x ζ , ρ, θ ) = ˜hμν (x ζ )
(35)
where l is an integer and 0 ≤ θ ≤ 2π, and imposing the
mass condition
4
the radial modes satisfy the Sturm–Liouville equation
˜hμν (x ζ ) = m2 ˜hμν (x ζ ),
(36)
(34)
is an effective mass con-
taining orbital angular momentum contributions l and it
behaves as a position dependent mass. Note that we have
ρ2
d
dρ
φ (ρ)
1
ρ
− 5
2
φ (ρ) +
d2
c tanh2(cρ)
dρ2
+ M 2(ρ)ecρ−tanh cρ φ (ρ) = 0.
m2 − l2
The factor M 2(ρ) =
(37)
a degenerate KK spectrum, as in the GS model [4]. How-
ever, since limρ→∞ M 2(ρ) = m2, the degeneracy is broken
for large distances.
Due to the axial symmetry, we impose the Neumann
boundary conditions on φm [4,36]
φ
(∞) = 0.
(0) = φ
m
m
(38)
Furthermore, these modes satisfy the following orthonormal-
ity condition:
∞
γ (ρ)φ∗
m
φndρ = δmn.
σ (ρ)
0
(39)
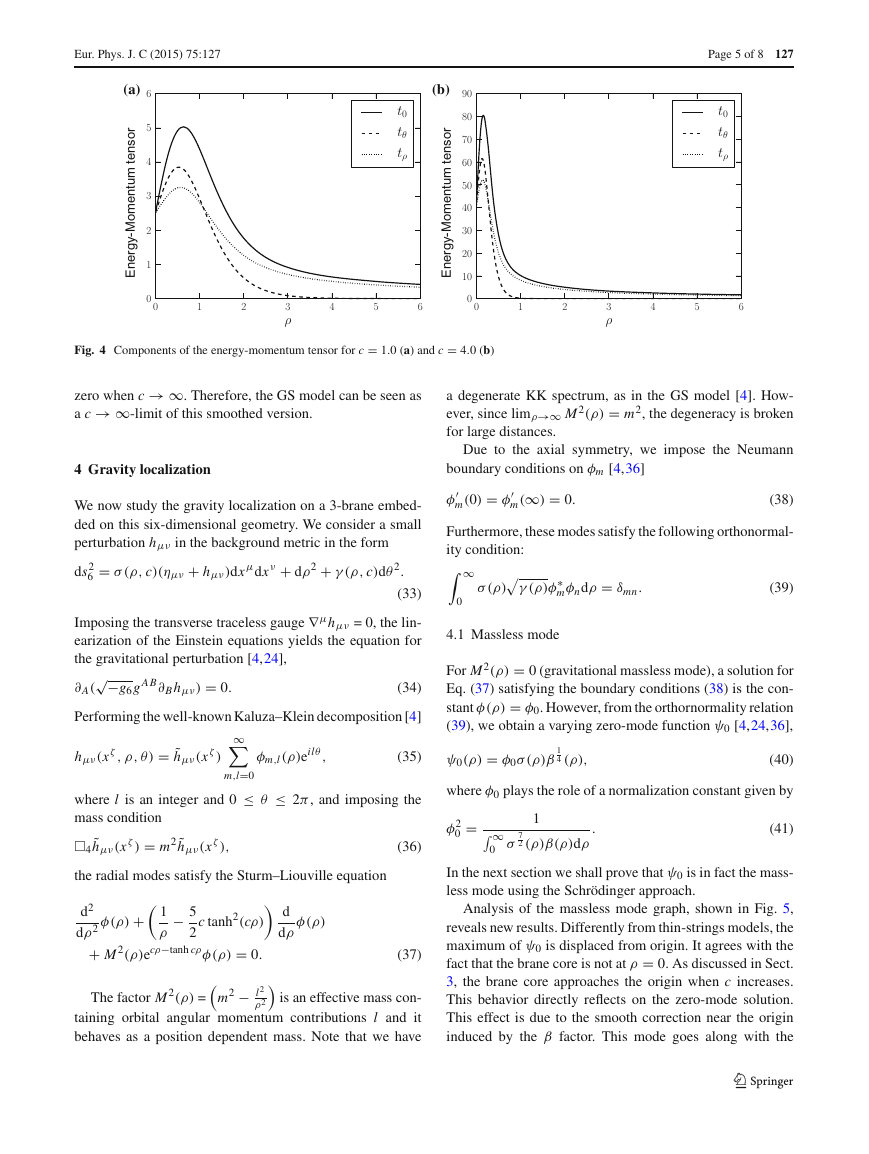
4.1 Massless mode
For M 2(ρ) = 0 (gravitational massless mode), a solution for
Eq. (37) satisfying the boundary conditions (38) is the con-
stant φ (ρ) = φ0. However, from the orthornormality relation
(39), we obtain a varying zero-mode function ψ0 [4,24,36],
ψ0(ρ) = φ0σ (ρ)β
where φ0 plays the role of a normalization constant given by
1
4 (ρ),
(40)
=
φ2
0
∞
0
1
σ
7
2 (ρ)β(ρ)dρ
.
(41)
In the next section we shall prove that ψ0 is in fact the mass-
less mode using the Schrödinger approach.
Analysis of the massless mode graph, shown in Fig. 5,
reveals new results. Differently from thin-strings models, the
maximum of ψ0 is displaced from origin. It agrees with the
fact that the brane core is not at ρ = 0. As discussed in Sect.
3, the brane core approaches the origin when c increases.
This behavior directly reflects on the zero-mode solution.
This effect is due to the smooth correction near the origin
induced by the β factor. This mode goes along with the
123
127 Page 6 of 8
Eur. Phys. J. C (2015) 75 :127
c
c
c
= 1
.0
= 2
.0
= 4.0
5
4
3
2
1
)
ρ
(
0
ψ
0
0
1
2
3
ρ
4
5
6
where C1 and C2 are arbitrary constants and Y is the Bessel
function of second kind.
In order to obtain a complete domain solution, we inte-
grated Eq. (37) numerically. For this purpose, we used the
matrix method [37] with second order truncation error for
the domain ρ ∈ [0, 6]. We have plotted in Fig. 6 numeri-
cal solutions for c = 1.0, comparing with the analytical GS
model solution (44). Near the origin, the solutions behave as
a Bessel function, whereas far from the brane, they behave as
the GS massive modes solutions. The main advantage of the
numerical approach is that we obtain the full domain solu-
tion, so we may construe inside brane massive gravitons. In
contrast to the thin-string model, the massive solutions are
non-zero with a high amplitude near the brane.
Fig. 5 Gravitational massless mode
4.3 Analog quantum potential
energy-momentum tensor. As c increases, the maximum of
the zero mode and the energy density tend to coincide.
Therefore, our smoothed model provides a near brane cor-
rection to the massless gravitational mode, smoothens the
zero mode in the boundary of the core, and recovers the thin-
string exponential behavior for large distances.
4.2 Massive modes
Solutions of Eq. (37) for M 2(ρ) = 0, called massive modes,
are difficult to obtain analytically. Before embarking on a
numerical analysis two different regimes are studied.
Firstly, we analyze the graviton massive modes near the
brane (ρ → 0). In this limit, the differential equation (37) is
reduced to a Bessel equation
d2
dρ2
φ (ρ) + 1
ρ
d
dρ
φ (ρ) + M 2(ρ)φ (ρ) = 0,
(42)
which solutions satisfying the boundary conditions (38) are
given by the Bessel functions of first kind Jl (mρ). Further-
more, the boundary condition (38) excludes the l = 1 solu-
tion; then p-waves are not allowed.
(43)
Asymptotically (ρ → ∞), Eq. (37) becomes
φ (ρ) − 5c
d2
dρ2
2
2ecρ φ (ρ) = 0,
φ (ρ) + m
d
dρ
√
= m/
with a non-degenerate re-scaled mass m
e. This
equation is exactly the same as the GS model, of which the
solution is [4]
φm (ρ) = e(5/4)cρ
+C2Y5/2
C1 J5/2
e(c/2)ρ
e(c/2)ρ
2m
c
(44)
,
2m
c
123
Another way to study massive modes is to turn the KK equa-
tion (37) into a Schrödinger-like equation. This formalism
provides information as regards massive states that interact
with the brane. Firstly, we perform a change of the indepen-
dent variable, given in Eq. (22), which provides a conformally
plane metric [24,36]. Then we write φ (z) as
φm (z) =
ψm (z),
(45)
1
σ (z)β
1
4 (z)
which turns Eq. (37) into a Schrödinger equation for the
ψm (z) function
− ¨ψm (z) + U (z)ψm (z) = m2ψm (z),
(46)
where the dots represent derivatives with respect to the z
coordinate. The potential function has the form
+ l2
2 + 1
U (z) = ¨σ
˙β
(47)
¨β
˙β
˙σ
.
+ 1
2
σ
σ
β
− 3
16
β
4
β
β
From Eq. (45), we conclude that the massless mode defined in
Eq. (40) satisfies the analog Schrödinger equation for m = 0.
The potential can be rewritten in the ρ coordinate as
¯U (ρ; c, l) = e
−(cρ−tanh cρ)
− 2c2 tanh(cρ)sech2(cρ)
c2 tanh4(cρ) − 5c
4
+ 3
2
+ l2e(cρ−tanh cρ)
ρ2
tanh2(cρ)
ρ
− 1
4ρ2
.
(48)
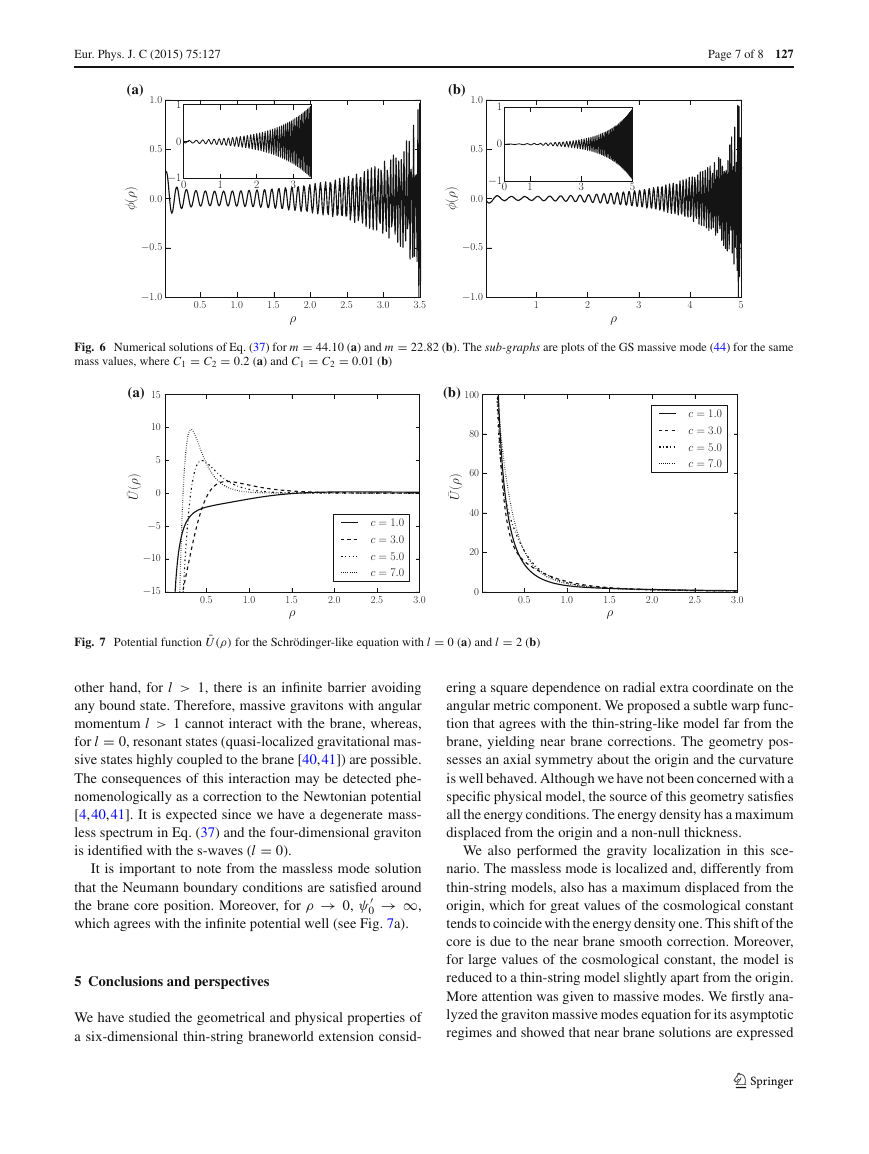
We have plotted the potential ¯U (ρ) given by Eq. (48) in Fig. 7.
For l = 0 we have a potential well near the origin, showing
the possibility arises of bound states where massive gravi-
tons may interact with the brane as resonant states [38,39].
As c increases, a barrier is formed besides the origin. On the
Eur. Phys. J. C (2015) 75 :127
Page 7 of 8 127
1
0
−1
0
(a)
1.0
)
ρ
(
φ
0.5
0.0
−0.5
−1.0
1
2
3
0.5
1.0
1.5
2.0
2.5
3.0
3.5
ρ
(b)
1.0
)
ρ
(
φ
0.5
0.0
−0.5
−1.0
1
0
−1
0
1
3
5
1
2
3
4
5
ρ
Fig. 6 Numerical solutions of Eq. (37) for m = 44.10 (a) and m = 22.82 (b). The sub-graphs are plots of the GS massive mode (44) for the same
mass values, where C1 = C2 = 0.2 (a) and C1 = C2 = 0.01 (b)
(a)
15
)
ρ
(
¯U
10
5
0
−5
−10
−15
(b)
100
)
ρ
(
¯U
80
60
40
20
0
c
c
c
c
= 1
= 3
= 5
= 7
.0
.0
.0
.0
0.5
1.0
1.5
ρ
2.0
2.5
3.0
c
c
c
c
= 1
.0
= 3
.0
= 5
.0
= 7.0
0.5
1.0
1.5
ρ
2.0
2.5
3.0
Fig. 7 Potential function ¯U (ρ) for the Schrödinger-like equation with l = 0 (a) and l = 2 (b)
other hand, for l > 1, there is an infinite barrier avoiding
any bound state. Therefore, massive gravitons with angular
momentum l > 1 cannot interact with the brane, whereas,
for l = 0, resonant states (quasi-localized gravitational mas-
sive states highly coupled to the brane [40,41]) are possible.
The consequences of this interaction may be detected phe-
nomenologically as a correction to the Newtonian potential
[4,40,41]. It is expected since we have a degenerate mass-
less spectrum in Eq. (37) and the four-dimensional graviton
is identified with the s-waves (l = 0).
It is important to note from the massless mode solution
that the Neumann boundary conditions are satisfied around
→ ∞,
the brane core position. Moreover, for ρ → 0, ψ
which agrees with the infinite potential well (see Fig. 7a).
0
5 Conclusions and perspectives
We have studied the geometrical and physical properties of
a six-dimensional thin-string braneworld extension consid-
ering a square dependence on radial extra coordinate on the
angular metric component. We proposed a subtle warp func-
tion that agrees with the thin-string-like model far from the
brane, yielding near brane corrections. The geometry pos-
sesses an axial symmetry about the origin and the curvature
is well behaved. Although we have not been concerned with a
specific physical model, the source of this geometry satisfies
all the energy conditions. The energy density has a maximum
displaced from the origin and a non-null thickness.
We also performed the gravity localization in this sce-
nario. The massless mode is localized and, differently from
thin-string models, also has a maximum displaced from the
origin, which for great values of the cosmological constant
tends to coincide with the energy density one. This shift of the
core is due to the near brane smooth correction. Moreover,
for large values of the cosmological constant, the model is
reduced to a thin-string model slightly apart from the origin.
More attention was given to massive modes. We firstly ana-
lyzed the graviton massive modes equation for its asymptotic
regimes and showed that near brane solutions are expressed
123
127 Page 8 of 8
Eur. Phys. J. C (2015) 75 :127
in terms of Bessel functions of the first kind for angular
momentum values l = 1. Far from the brane, we recover the
Gherghetta–Shaposhnikov thin-string model without degen-
erate states. Numerical solutions of the equation for the mas-
sive modes revealed that, in contrast to the thin-string model,
the massive solutions have a considerable amplitude near
the brane, indicating the possibility of gravitational massive
states interacting with the defect. This result was reinforced
from a Schödinger approach, where we have studied the ana-
log quantum potential. From this formalism we proved the
massless mode, which must satisfy a Schödinger-like equa-
tion for m = 0. We also concluded that massive states may
interact with the brane only for l = 0 which refers to four-
dimensional gravitons.
As a future perspective, the KK spectrum can be achieved
from the analog quantum potential by means of suitable
numerical methods to predict corrections to the Newtonian
potential.
Acknowledgments The authors are grateful to the Brazilian agencies
CNPq, CAPES, and FUNCAP for financial support.
Open Access This article is distributed under the terms of the Creative
Commons Attribution License which permits any use, distribution, and
reproduction in any medium, provided the original author(s) and the
source are credited.
Funded by SCOAP3 / License Version CC BY 4.0.
References
1. L. Randall, R. Sundrum, Phys. Rev. Lett. 83, 3370 (1999)
2. L. Randall, R. Sundrum, Phys. Rev. Lett. 83, 4690 (1999)
3. I. Olasagasti, A. Vilenkin, Phys. Rev. D 62, 044014 (2000)
4. T. Gherghetta, M.E. Shaposhnikov, Phys. Rev. Lett. 85, 240 (2000)
5. E. Ponton, E. Poppitz, JHEP 0102, 042 (2001)
6. A.G. Cohen, D.B. Kaplan, Phys. Lett. B 470, 52 (1999)
7. R. Gregory, Phys. Rev. Lett. 84, 2564 (2000)
8. I. Oda, Phys. Lett. B 496, 113 (2000)
9. Y.X. Liu, L. Zhao, Y.S. Duan, JHEP 0704, 097 (2007)
10. P. Tinyakov, K. Zuleta, Phys. Rev. D 64, 025022 (2001)
11. M. Giovannini, H. Meyer, M.E. Shaposhnikov, Nucl. Phys. B 619,
615 (2001)
12. B. de Carlos, J.M. Moreno, JHEP 0311, 040 (2003)
13. A. Kehagias, Phys. Lett. B 600, 133 (2004)
14. J. Garriga, M. Porrati, JHEP 08, 028 (2004)
15. M. Gogberashvili, P. Midodashvili, D. Singleton, JHEP 0708, 033
(2007)
16. E. Papantonopoulos, A. Papazoglou, JCAP 0507, 004 (2005)
17. P. Bostock, R. Gregory, I. Navarro, J. Santiago, Phys. Rev. Lett. 92,
221601 (2004)
18. G. Kofinas, Phys. Lett. B 633, 141 (2006)
19. S. Kanno, J. Soda, JCAP 0407, 002 (2004)
20. J.M. Cline, J. Descheneau, M. Giovannini, J. Vinet, JHEP 0306,
048 (2003)
21. E. Papantonopoulos, A. Papazoglou, V. Zamarias, Nucl. Phys. B
797, 520 (2008)
22. I. Navarro, JCAP 0309, 004 (2003)
23. I. Navarro, J. Santiago, JHEP 0502, 007 (2005)
24. J.E.G. Silva, C.A.S. Almeida, Phys. Rev. D 84, 085027 (2011)
25. E. Witten, Adv. Theor. Math. Phys. 2, 253 (1998)
26. K. Becker, M. Becker, J. Schwarz, String Theory and M-Theory,
A Modern Introduction (Cambridge University Press, Cambridge,
2007)
27. J.M. Maldacena, Int. J. Theor. Phys. 38, 1113 (1999)
28. J.M. Maldacena, Adv. Theor. Math. Phys. 2, 231 (1998)
29. W. Israel, Phys. Rev. D 15 (1974)
30. A. Vilenkin, Phys. Rev. Lett. 46, 1169 (1981)
31. J. Gott III, Astrophys. J. 288, 422 (1985)
32. W.A. Hiscock, Phys. Rev. D 31, 3288 (1985)
33. M. Christensen, A.L. Larsen, Y. Verbin, Phys. Rev. D 60 (1999)
34. A.G. Cohen, D.B. Kaplan, Phys. Lett. B 215, 67 (1988)
35. R. Gregory, Phys. Lett. B 215, 663 (1988)
36. J.E.G. Silva, V. Santos, C.A.S. Almeida, Class. Quantum Gravity
30, 025005 (2013)
37. P. Amodio, G. Settanni, J. Numer. Anal. Ind. Appl. Math. 6(1–2),
1–13 (2011)
38. C.A.S. Almeida, M.M. Ferreira Jr, A.R. Gomes, R. Casana, Phys.
Rev. D 79, 125022 (2009)
39. W.T. Cruz, L.S.J. Sousa, R.V. Maluf, C.A.S. Almeida, Phys. Lett.
B 730, 314–319 (2014)
40. C. Csaki, J. Erlich, T.J. Hollowood, Y. Shirman, Nucl. Phys. B 581,
309 (2000)
41. C. Csaki, J. Erlich, T.J. Hollowood, Phys. Rev. Lett. 84, 5932 (2000)
123
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
