logo资料库

考虑电价不确定性的主动配电网网损成本鲁棒优化模型.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：1.66M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    第 37 卷第 9 期 ２０17 年 9 月 电 力 自 动 化 设 备 Ｅｌｅｃｔｒｉｃ Ｐｏｗｅｒ Ａｕｔｏｍａｔｉｏｎ Ｅｑｕｉｐｍｅｎｔ Ｖｏｌ．37 Ｎｏ．9 Sept. ２０17 考虑电价不确定性的主动配电网网损成本鲁棒优化模型 张旭东 1，王昊婧 2，武 赓 3，曾 鸣 3，周 旋 4 （1． 华北电力大学 经济与管理学院，北京 102206； 2． 国网北京市电力公司 北京电力经济技术研究院，北京 100055； 3． 华北电力大学 新能源电力系统国家重点实验室，北京 102206；4． 上海电机学院 电气学院，上海 200245） 摘要： 提高配电网的运行效率和可靠性是配电网运营商优化系统运行的主要目标，在开放电力市场中，市场 电价波动可能会使得上述优化目标下不能够最小化配电网的网损成本。 基于此，构建考虑电价不确定性的配 电网运营商网损成本鲁棒优化模型。 分析不同优化目标下电价波动以及需求响应和储能调度策略对配电网 运行网损成本的影响，并给出在不同情境下的最优运行策略。 IEEE 33 节点配电网的仿真结果验证了所提模 型的有效性。 关键词： 主动配电网； 配电网运营商； 网损成本； 储能； 需求响应； 鲁棒优化； 模型 中图分类号： TM 761 文献标识码： A DOI： 10.16081 ／ j.issn.1006－6047.2017.09.0１８ 0 引言 随着不同类型的分布式电源和储能的大规模接 入，传统被动的配电网运行管理模式将逐步向主动 管理调控转变，主动配电网 ADN（Active Distribution Network）的概念被提出 ［1鄄2］。 基于国际大电网会议提 出 的 ADN 的 基 本 内 涵 ，ADN 所 定 义 的 是 一 种 能 够 向上兼容主干电网，同时实现内部分布式电源、储能 以及可调控负荷协调控制，具备开放体系架构的配 电网形态，是未来保证可再生能源高效利用、实现系 统源-网-荷-储协调优化的重要技术实现手段 ［3鄄5］。 在当前我国电力体制改革不断深入、电力市场建 设不断完善的背景下，电力配售业务将初步放开，配电 网系统中分布式电源、储能、电网可能由不同的主体 投资建设 ［6 鄄 7］。 未来配电网运营商 DNO（Distribution Network Operator）将 承 担 配 电 网 的 管 理 调 控 任 务 ， 其作为独立的市场主体，会从自身经营效益出发，依 据市场电价以及配电网中的可调控资源 ，制定自身 最优的运行管理策略［8鄄9］。 因此，研究未来 ADN 背景 下 DNO 的最优运行管理策略 ，对于提高 DNO 对 配 电网的运行管理效率、促进我国电力市场的健康有 序发展都具有重要的意义。 国内外学者对储能、需求响应 DR（Demand Res鄄 ponse）资源的调控策略以及市场电价对配电网网损 的影响进行了较多的研究。 文献［10］提出了一种计 及网损的配电网电池储能站运行优化模型，通过构建 双层的优化模型分析了电池储能选址以及运行方案 收稿日期：２01７ － ０1 － １９；修回日期：２01７ - 07 - ０４ 基金项目：中央高校基本科研业务费专项资金资助项目（2016鄄 XS80） Project supported by the Fundamental Research Funds for the Central Universities（2016XS80） 对于配电网网损的影响，为制定配电网短期以及中长 期运行策略提供了相应的决策参考。 文献［11］以配 电网运行网损最小为目标，在对系统内负荷弹性分析 的基础上，构建了配电网中 DR 资源调控策略和最优 定价模型。 文献［12］在对 DR 资源激励机制分类的 基础上，以用户用电成本最小为目标构建了智能电网 中 DR 资源最优调控策略模型。 文献［13］在对价格 响应型和直接 可 控 型 DR 资 源 建 模 分 析 的 基 础 上 ， 对比分析了以 DNO 运营成本最低、系统网损最小以 及用户用电成本最小 3 个目标下的 DR 资源运行调 控策略以及对系统运行的影响，但在 DNO 网损成本 的建模中使用了固定电价，没有考虑电价波动对于上 述目标的影响。 文献［14］分别以用户用电成本最小 和系统供电成本最小为目标构建了考虑 DR 资源的 微网运行优化模型，主要研究了 DR 对系统中各类型 发电资源运行经济性的影响 。 文献 ［15 鄄16］在 对 系 统网损成本的建模中也使用了固定的市场电价 ，并 没有考虑电价不确定性对于网损成本的影响。 综上所述，针对电价波动对 DNO 网损成本以及 对 ADN 中 储 能 和 DR 调 度 策 略 影 响 的 研 究 还 比 较 少。 基于此，本文构建了考虑电价不确定性的 DNO 网损成本鲁棒优化模型，在 IEEE 33 节点配电网系统 中对上述模型进行仿真计算 ，对比分析了以网损最 小和以网损成本最低为目标的 2 种配电网运行策略 下 储 能 和 DR 的 调 度 策 略 以 及 不 同 情 景 下 ADN 的 网损成本。 1 考虑储能和 DR 的 ADN 调控策略模型 在 ADN 的 背 景 下 ，DNO 能 够 通 过 信 息 与 通 信 技 术 ICT （Information and Communications Techno鄄 logy）和先进的自动控制技术对系统中储能和可调控
    电 力 自 动 化 设 备 第 37 卷 DR 资源进行主动管理，以实现自身经营效益最优 ， ADN 为 实 现 配 电 网 的 精 细 化 管 理 提 供 了 相 应 的 技 术支持和管理模式［15］。 在传统的配电网运行策略下， DNO 往 往 会 以 网 损 最 小 为 目 标 对 配 电 网 运 行 策 略 进行优化，其目标函数可表示为： min E grid T loss =鄱 t＝1 n t 鄱 i＝1 P grid i，t + E loss t  （1） loss 为配电网运行网损；P grid i，t 为 t 时段节点 i 处 t 为 t 时段储能充放电能量损耗；T 其中，E grid 的净有功功率；E loss 为时段数；n 为节点数。 在 电 力 市 场 环 境 下 ，DNO 作 为 独 立 的 市 场 主 体，是市场价格的承担者，系统网损以及市场电价波 动都会对其网损成本产生影响，因此，在电价波动条 件下，配电网运行优化的目标函数可表示为： T min Closs=鄱 t＝1 t t n 鄱 i＝1 P grid i，t + E loss t tp軌t  （2） 其中，Closs 为配电网运行网损成本； p軌t 为日前市场 t 时 段的单位电价。 a. 潮流约束。 i，t - P EVC i，t + P EVD i，t P grid Q grid P grid i，t = P G i，t = Q G i，t - P D i，t - Q D i，t i，t = Ui，t 鄱 jN（i ） Yij Uj，t cos（δ i，t - δj，t - θij） Q grid i，t = Ui，t 鄱 jN（i ） Yij Uj，t sin（δ i，t - δj，t - θij） Ui，min≤Ui，t≤Ui，max （3） （4） （5） （6） （7） （8） l  Ω L Il，t ≤I l i，t 、Q grid i，t 、P EVD 其 中 ，P grid i，t 分 别 为 节 点 i 处 的 净 有 功 和 无 功 功 率；δ i，t 为节点 i 的电压相角；N（i）表示与节点 i 连接 的节点集合；P EVC i，t 分别为节点 i 处储能在 t 时段 内的充电和放电速率；P G i，t 分别为节点 i 处主网 供应或者分布式电源的有功和无功功率；P D i，t 分 别 为 节 点 i 处 负 荷 的 有 功 和 无 功 功 率 ；Ui，t 为 节 点 i 处的电压；Yi j、θi j 分别为导纳矩阵第 i 行 j 列元素的 导纳值和相角；Ui，max、Ui，min 分别为电压上、下限；Il，t 为 i，t、Q G i，t、Q D 线路 l 在 t 时段的载流量；I l 为线路 l 允许最大载流 量。 约束式（7）和约束式（8）分别表示节点 i 处的电 压约束和线路 l 的电流约束。 b. 储能充放电约束。 ／ rdis）Δt i，t ≤Rdis i，t ≤Rchg i，min≤P EVD i，t rchg- P EVD i，t i，min≤P EVC t = P EVC i，max， Rdis i，t （1- rchg） + P EVD SOC（t）i = SOC（t -1）i +（P EVC SOCi，min≤SOC（t）i≤SOCi，max Rchg E loss （9） （10） （11） （12） 其 中 ，SOC（t）i 为 节 点 i 处 储 能 在 t 时 段 所 储 电 量 ； SOCi，max、SOCi，min 分 别 为 节 点 i 处 储 能 的 最 大 和 最 小 可储电量 ；Δt 为储能在 t 时段内的充放电时长 ；rchg、 rdis 分别为储能的充、放电效率；Rchg i，min 分别为节 点 i 处储能最大和最小充电速率；Rdis i，min 分别为 i，t （1- rdis） ／ rdis i，max、Rchg i，max、Rdis i，max 最大和最小放电速率。 c. DR 约束。 本文中假设 DNO 与配电网区域内的负 荷 集 成 商 或 者 具 有 较 大 DR 资 源 的 负 荷 集 成 商 事 先 签 订 DR 合 同 ，确 定 各 节 点 DR 最 大 参 与 比 例 ，因 此 ，DR 约束可表示为： P D P D0 i，t （14） （13） i，t， ε min i，t 和 ε min i，t ≤εi，t≤ε max i，t T i，t≥η i鄱 t＝1 i，t = （1- κi，t εi，t）P D0 P D T 鄱 t＝1 其中，P D0 i，t 为节点 i 处不参与 DR 时的初始有功功率； εi，t 表 示 节 点 i 处 负 荷 在 t 时 段 的 DR 参 与 程 度 ；κi，t 为节点 i 处负荷在 t 时段是否参与 DR 的 0-1 决 策 变量；ε max i，t 表示节点 i 处用户在 t 时段参与 DR 的程度，即 DR 所占原始负荷比例的上、下限约束；ηi 为节点 i 处参与 DR 的比例限制。 约束式（14）表示 节点 i 处负荷参与 DR 后在 T 个时段内用电量应不 低于原始负荷的一定比例，从而保证用户参与 DR 后 整体的用电满意度。 用户参与 DR 的比例限制由用 户根据 DNO 或者负荷集成商给出的激励价格和自 身用电负荷需求决定。 2 考虑日前市场电价波动的鲁棒优化模型 在电力市场环境下，DNO 会根据日前市场的预 测电价制定第二天的配电网运行策略。 由于电价预 测存在误差，DNO 需要在制定运行策略时考虑电价 波 动 的 不 确 定 性 ，从 而 降 低 自 身 经 营 风 险 ，因 此 本 文 引 入 了 考 虑 电 价 不 确 定 性 的 配 电 网 运 行 鲁 棒 优 化模型。 假设日前市场 t 时段电价的预测值为 p軌t，用区间 数来表示实际电价的不确定性 ，则电价波动可表示 为 p軌t ψ（ p軌t）=｛p min t 分别为日 前市场预测电价的最大和最小值。 对于 DNO 而言， 当市场中某时段的电价低于预测电价时，执行之前的 t ｝，其中 p max t ≤p軌t≤p max t 、p min 优化策略，DNO 所需承担的网损成本会较之前所得 的优化结果有所下降，即不会影响之前运行策略所造 成的网损成本对于电价波动的鲁棒性，因为电价向下 波动不会影响鲁棒模型所确定的“最差情况”的结果。 因此，本文中只考虑电价向上波动的情况，电价的不 确定性可表示为： pt = p軌t+ μ t（ pmax 0≤ μ t≤1 t - p軌t） （15） （16） 其中， μ t 为电价预测误差因子。 式（16）表示市场电 价 pt 的不确定性约束。 基于上述对电价不确定性的假设和建模 ，对于 DNO 而言，需要保证优化后的运营策略能够在最大 的电价波动程度下使自身运营成本最小，因此考虑电
    第 9 期 张旭东，等：考虑电价不确定性的主动配电网网损成本鲁棒优化模型 价不确定性的配电网运行鲁棒优化模型可表示为： min i，t ，E loss P grid t max μt T Closs =鄱 t＝1 n t 鄱 i＝1 P grid i，t + E loss t ［p軌t + μ t（ pmax t - p軌t）］ （17） s.t. 0≤ μ t≤1 μ t≤祝 T 鄱 t＝1 约束式（３）—（１5） （18） 其中，祝 表示鲁棒优化解的保守程度，即该运行策略 对于电价波动程度的可接受程度，根据 μ t 的取值范 围，祝 可取 0 ~ 24 之间的正整数。 n 为 简 化 模 型 表 达 形 式 ，设 ft =鄱 i＝1 pmax t - p軌t，则内层优化问题可表示为： P grid i，t + E loss t ，Δpt = max μt s.t. f *Δp μT E Y μ≤ Y T 祝 祝 （19） （20） 其中 ， f 表 示 向 量 （ f1， f２，… ， fＴ），Δ p 表 示 向 量 （Δp1， Δp２，…，ΔpＴ），f *Δp 表示 f 与 Δp 的 Ｈadamard 乘积； μ 表示向量（ μ１， μ２，…， μＴ）；E 为标准对角矩阵；Y 表 示全 1 横向量。 根据线性规划中的强对偶理论 ，内 层的优化问题可转化为： min β≥０，λ ［Y，祝 ］ λ β 祝 s.t. E Y 祝T λ β 祝≥［ f*Δp］T （21） （22） 其中，λ 表示向量（λ１，λ２，…，λＴ）；λt（t=1，2，…，T）、β 为 内层优化问题的对偶变量。 上述优化问题可表示为： min i，t ，E loss P grid t min λt T Closs =鄱 t＝1 （ ft p軌t + λt） + β祝 （23） s.t. 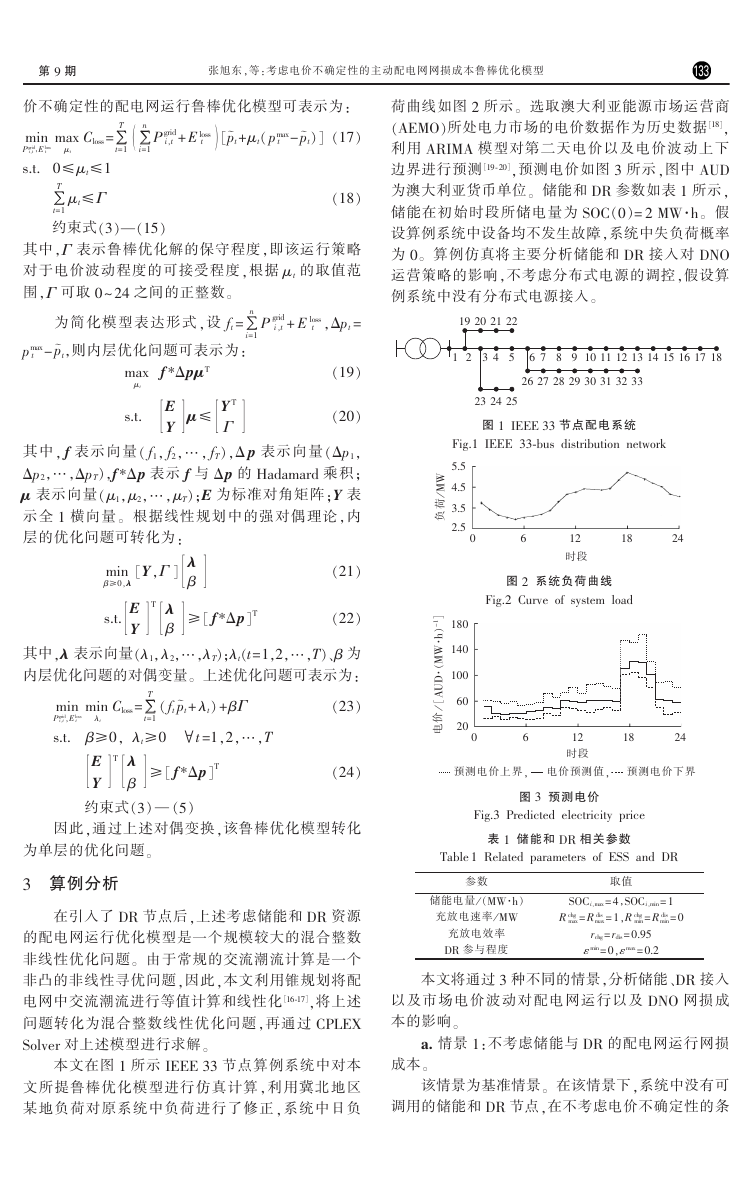β≥0， λt≥0 坌t =1，2，…，T E YY 祝T λ β 祝≥［ f*Δp］T 荷曲线如图 2 所示。 选取澳大利亚能源市场运营商 （AEMO）所处电力市场的电价数据作为历史数据 ［18］， 利用 ARIMA 模型对第二天电价以及电价波动上下 边界进行预测 ［19鄄20］，预测电价如图 3 所示，图中 AUD 为澳大利亚货币单位。 储能和 DR 参数如表 1 所示， 储能在初始时段所储电量为 SOC（0）= 2 MW·h。 假 设算例系统中设备均不发生故障，系统中失负荷概率 为 0。 算例仿真将主要分析储能和 DR 接入对 DNO 运营策略的影响，不考虑分布式电源的调控，假设算 例系统中没有分布式电源接入。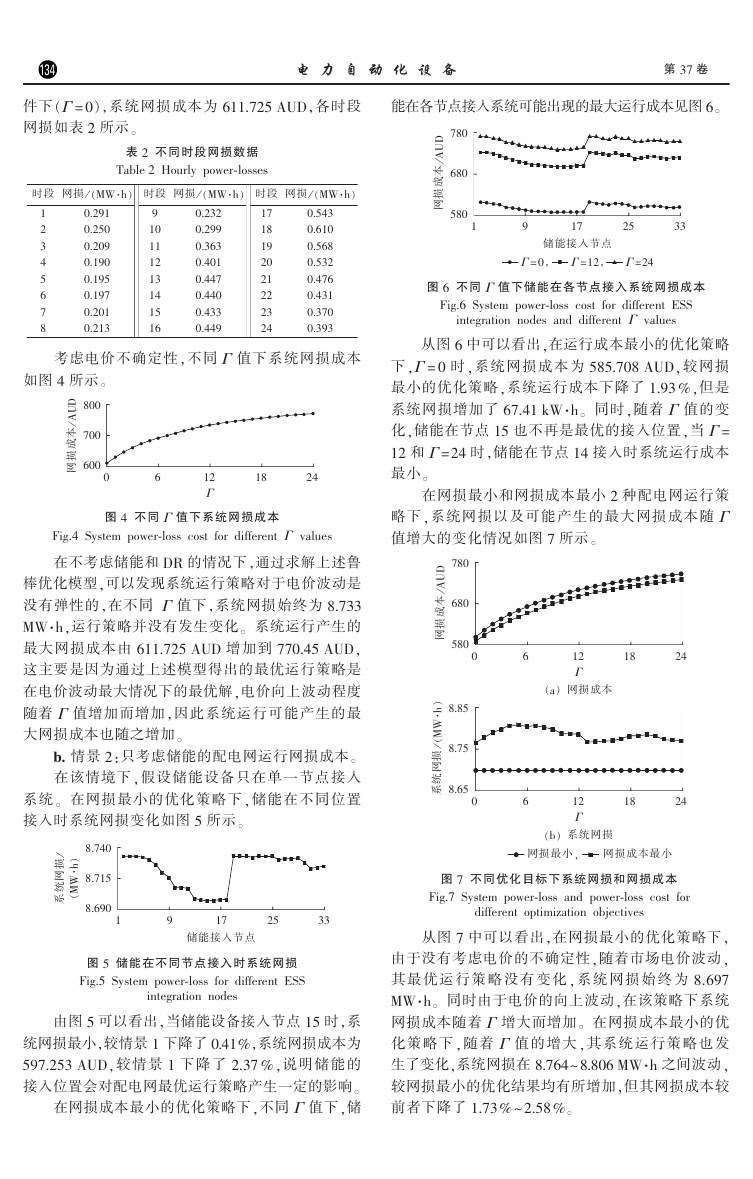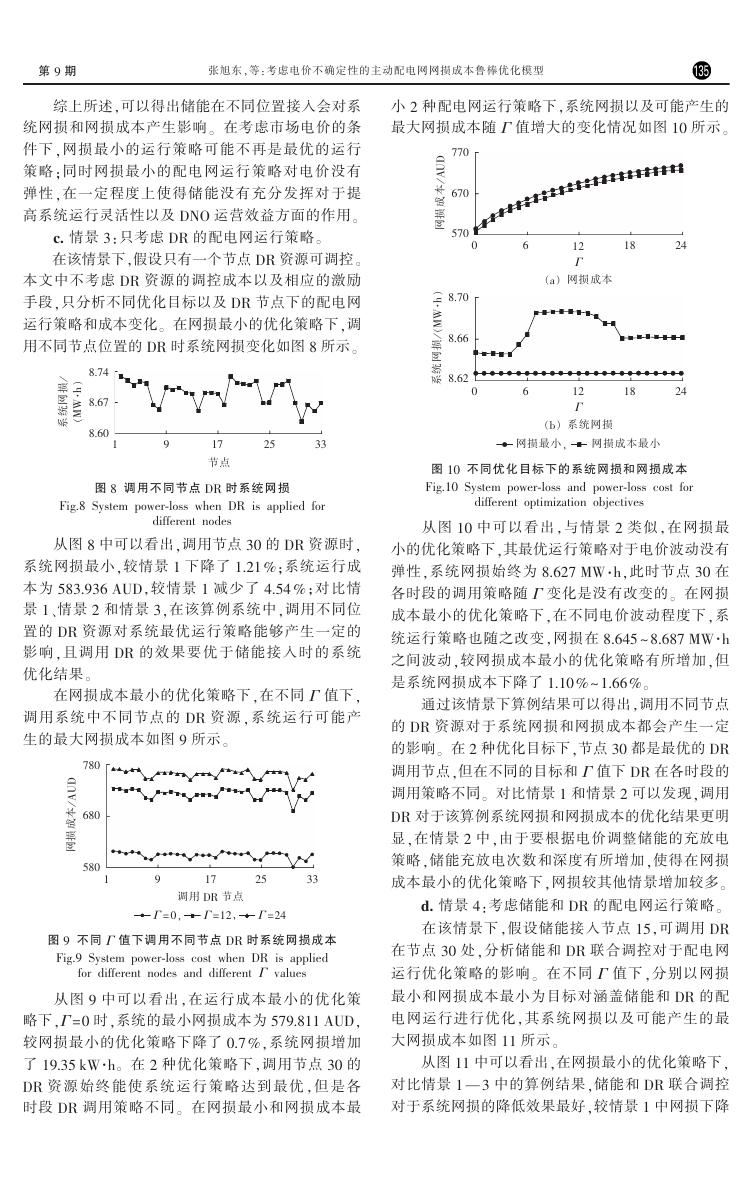 19 20 21 22 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 26 27 28 29 30 31 32 33 23 24 25 图 1 IEEE 33 节点配电系统 Ｆｉｇ．1 IEEE 33鄄bus distribution network W M ／ 荷 负 5.5 4.5 3.5 2.5 ］ 1 - ） h · W M （ · D U A ［ ／ 价 电 180 140 100 60 20 0 6 12 时段 18 24 图 2 系统负荷曲线 Ｆｉｇ．2 Curve of system load 0 6 12 时段 18 24 （24） 预测电价上界， 电价预测值， 预测电价下界 约束式（３） — （５） 因此，通过上述对偶变换，该鲁棒优化模型转化 为单层的优化问题。 3 算例分析 在引入了 DR 节点后，上述考虑储能和 DR 资源 的配电网运行优化模型是一个规模较大的混合整数 非线性优化问题。 由于常规的交流潮流计算是一个 非凸的非线性寻优问题，因此，本文利用锥规划将配 电网中交流潮流进行等值计算和线性化 ［16鄄17］，将上述 问题转化为混合整数线性优化问题，再通过 CPLEX Solver 对上述模型进行求解。 本文在图 1 所示 IEEE 33 节点算例系统中对本 文所提鲁棒优化模型进行仿真计算 ，利用冀北地区 某地负荷对原系统中负荷进行了修正 ，系统中日负 图 3 预测电价 Ｆｉｇ．3 Predicted electricity price 表 1 储能和 DR 相关参数 Table 1 Related parameters of ESS and DR 参数 取值 储能电量 ／ （MW·h） 充放电速率 ／ MW 充放电效率 DR 参与程度 R chg min= 0 SOC i，max= 4，SOC i，min= 1 max= R dis min= R dis max= 1，R chg rchg = rdis = 0.95 ε min= 0，ε max= 0.2 本文将通过 3 种不同的情景，分析储能、DR 接入 以及市场电价波动对配电网运行以及 DNO 网损成 本的影响。 a. 情景 1：不考虑储能与 DR 的配电网运行网损 成本。 该情景为基准情景。 在该情景下，系统中没有可 调用的储能和 DR 节点，在不考虑电价不确定性的条
    电 力 自 动 化 设 备 第 37 卷 件下（祝 = 0），系统网损成本为 611.725 AUD，各时段 网损如表 2 所示。 表 2 不同时段网损数据 Table 2 Hourly power鄄losses 时段 网损 ／ （MW·h） 时段 网损 ／ （MW·h） 时段 网损 ／ （MW·h） 1 2 3 4 5 6 7 8 0.291 0.250 0.209 0.190 0.195 0.197 0.201 0.213 9 10 11 12 13 14 15 16 0.232 0.299 0.363 0.401 0.447 0.440 0.433 0.449 17 18 19 20 21 22 23 24 0.543 0.610 0.568 0.532 0.476 0.431 0.370 0.393 考虑电价不确定性，不同 祝 值下系统网损成本 如图 4 所示。 800 D U A ／ 700 本 成 损 600网 0 6 12 祝 18 24 图 4 不同 祝 值下系统网损成本 Ｆｉｇ．4 System power鄄loss cost for different 祝 values 在不考虑储能和 DR 的情况下，通过求解上述鲁 棒优化模型，可以发现系统运行策略对于电价波动是 没有弹性的，在不同 祝 值下，系统网损始终为 8.733 MW·h，运行策略并没有发生变化。 系统运行产生的 最大网损成本由 611.725 AUD 增加到 770.45 AUD， 这主要是因为通过上述模型得出的最优运行策略是 在电价波动最大情况下的最优解，电价向上波动程度 随着 祝 值增加而增加，因此系统运行可能产生的最 大网损成本也随之增加。 b. 情景 2：只考虑储能的配电网运行网损成本。 在该情境下，假设储能设备只在单一节点接入 系统。 在网损最小的优化策略下 ，储能在不同位置 接入时系统网损变化如图 5 所示。 8.740 8.715 ／ 损 网 统 系 ） h · W M （ 8.690 1 9 17 25 33 储能接入节点 图 5 储能在不同节点接入时系统网损 Ｆｉｇ．5 System power鄄loss for different ESS integration nodes 由图 5 可以看出，当储能设备接入节点 15 时，系 统网损最小，较情景 1 下降了 0.41%，系统网损成本为 597.253 AUD，较 情 景 1 下 降 了 2.37 %，说 明 储 能 的 接入位置会对配电网最优运行策略产生一定的影响。 在网损成本最小的优化策略下，不同 祝 值下，储 能在各节点接入系统可能出现的最大运行成本见图 6。 D U A ／ 本 成 损 网 780 680 580 1 9 17 25 33 储能接入节点 祝 = 0， 祝 =12， 祝 =24 图 6 不同 祝 值下储能在各节点接入系统网损成本 Ｆｉｇ．6 System power鄄loss cost for different ESS integration nodes and different 祝 values 从图 6 中可以看出，在运行成本最小的优化策略 下 ，祝 = 0 时 ，系统网损成 本 为 585.708 AUD，较 网 损 最小的优化策略，系统运行成本下降了 1.93 %，但是 系统网损增加了 67.41 kW·h。 同时，随着 祝 值的变 化，储能在节点 15 也不再是最优的接入位置，当 祝 = 12 和 祝 = 24 时，储能在节点 14 接入时系统运行成本 最小。 在网损最小和网损成本最小 2 种配电网运行策 略下，系统网损以及可能产生的最大网损成本随 祝 值增大的变化情况如图 7 所示。 780 680 580 0 6 8.85 18 24 12 祝 （a） 网损成本 D U A ／ 本 成 损 网 ） h · W M （ ／ 8.75 损 网 统 8.65系 0 6 18 24 12 祝 （b） 系统网损 网损最小， 网损成本最小 图 7 不同优化目标下系统网损和网损成本 Ｆｉｇ．7 System power鄄loss and power鄄loss cost for different optimization objectives 从图 7 中可以看出，在网损最小的优化策略下， 由于没有考虑电价的不确定性，随着市场电价波动， 其 最 优 运 行 策 略 没 有 变 化 ，系 统 网 损 始 终 为 8.697 MW·h。 同时由于电价的向上波动，在该策略下系统 网损成本随着 祝 增大而增加。 在网损成本最小的优 化 策 略 下 ，随 着 祝 值 的 增 大 ，其 系 统 运 行 策 略 也 发 生了变化，系统网损在 8.764~8.806 MW·h 之间波动， 较网损最小的优化结果均有所增加，但其网损成本较 前者下降了 1.73 % ~ 2.58 %。
    第 9 期 张旭东，等：考虑电价不确定性的主动配电网网损成本鲁棒优化模型 综上所述，可以得出储能在不同位置接入会对系 统网损和网损成本产生影响。 在考虑市场电价的条 件下，网损最小的运行策略可能不再是最优的运行 策略；同时网损最小的配电网运行策略对电价没有 弹性，在一定程度上使得储能没有充分发挥对于提 高系统运行灵活性以及 DNO 运营效益方面的作用。 c. 情景 3：只考虑 DR 的配电网运行策略。 在该情景下，假设只有一个节点 DR 资源可调控。 本文中不考虑 DR 资源的调控成本以及相应的激励 手段，只分析不同优化目标以及 DR 节点下的配电网 运行策略和成本变化。 在网损最小的优化策略下，调 用不同节点位置的 DR 时系统网损变化如图 8 所示。 ／ 损 网 统 系 ） h · W M （ 8.74 8.67 8.60 1 9 17 节点 25 33 图 8 调用不同节点 DR 时系统网损 Ｆｉｇ．8 System power鄄loss when DR is applied for different nodes 从图 8 中可以看出，调用节点 30 的 DR 资源时， 系统网损最小，较情景 1 下降了 1.21 %；系统运行成 本为 583.936 AUD，较情景 1 减少了 4.54 %；对比情 景 1、情景 2 和情景 3，在该算例系统中，调用不同位 置的 DR 资源对系统最优运行策略能够产生一定的 影响 ，且调用 DR 的效 果 要 优 于 储 能 接 入 时 的 系 统 优化结果。 在网损成本最小的优化策略下，在不同 祝 值下， 调用系统中不同节点 的 DR 资 源 ，系 统 运 行 可 能 产 生的最大网损成本如图 9 所示。 780 680 D U A ／ 本 成 损 网 580 1 9 17 25 33 调用 DR 节点 祝 = 0， 祝 =12， 祝 =24 图 9 不同 祝 值下调用不同节点 DR 时系统网损成本 Ｆｉｇ．9 System power鄄loss cost when DR is applied for different nodes and different 祝 values 从图 9 中可以看出 ，在运行成本最小的优化策 略下，祝=0 时，系统的最小网损成本为 579.811 AUD， 较网损最小的优化策略下降了 0.7 %，系统网损增加 了 19.35 kW·h。 在 2 种优化策略下，调用节点 30 的 DR 资 源 始 终 能 使 系 统 运 行 策 略 达 到 最 优 ，但 是 各 时段 DR 调用策略不同。 在网损最小和网损成本最 小 2 种配电网运行策略下，系统网损以及可能产生的 最大网损成本随 祝 值增大的变化情况如图 10 所示。 770 670 570 0 6 8.70 18 24 12 祝 （a） 网损成本 D U A ／ 本 成 损 网 ） h · W M （ ／ 8.66 损 网 统 8.62系 0 6 18 24 12 祝 （b） 系统网损 网损最小， 网损成本最小 图 10 不同优化目标下的系统网损和网损成本 Ｆｉｇ．10 System power鄄loss and power鄄loss cost for different optimization objectives 从图 10 中可以看出 ，与情景 2 类似 ，在网损最 小的优化策略下，其最优运行策略对于电价波动没有 弹性，系统网损始终为 8.627 MW·h，此时节点 30 在 各时段的调用策略随 祝 变化是没有改变的。 在网损 成本最小的优化策略下，在不同电价波动程度下，系 统运行策略也随之改变，网损在 8.645 ~ 8.687 MW·h 之间波动，较网损成本最小的优化策略有所增加，但 是系统网损成本下降了 1.10 % ~ 1.66 %。 通过该情景下算例结果可以得出，调用不同节点 的 DR 资源对于系统网损和网损成本都会产生一定 的影响。 在 2 种优化目标下，节点 30 都是最优的 DR 调用节点，但在不同的目标和 祝 值下 DR 在各时段的 调用策略不同。 对比情景 1 和情景 2 可以发现，调用 DR 对于该算例系统网损和网损成本的优化结果更明 显，在情景 2 中，由于要根据电价调整储能的充放电 策略，储能充放电次数和深度有所增加，使得在网损 成本最小的优化策略下，网损较其他情景增加较多。 d. 情景 4：考虑储能和 DR 的配电网运行策略。 在该情景下，假设储能接入节点 15，可调用 DR 在节点 30 处，分析储能和 DR 联合调控对于配电网 运行优化策略的影响。 在不同 祝 值下，分别以网损 最小和网损成本最小为目标对涵盖储能和 DR 的配 电网运行进行优化，其系统网损以及可能产生的最 大网损成本如图 11 所示。 从图 11 中可以看出，在网损最小的优化策略下， 对比情景 1 — 3 中的算例结果，储能和 DR 联合调控 对于系统网损的降低效果最好，较情景 1 中网损下降
    电 力 自 动 化 设 备 第 37 卷 系统网损不仅取决于现阶段的系统运行情况 ，还受 下一时段运行状态的影响。 系统的调控策略可能需 要在某一低电价时段增加系统网损，从而保证在高电 价时段降低系统网损，降低系统整体的网损成本。 18 24 b. 不同负荷水平下的考虑储能和 DR 的配电网 780 660 540 0 6 8.75 12 祝 （a） 网损成本 D U A ／ 本 成 损 网 ） h · W M （ ／ 8.65 损 网 统 8.55系 运行策略分析。 基于算例中情景 4 中的基本情景假设 ，根据冀 北该地区在该月的实际负荷 ，选取了该地区该月最 大负荷日和最低负荷日 ，对比分析不同负荷水平下 2 种优化目标下的系统网损成本。 负荷曲线如图 12 所示。 在不同负荷水平下 ，系统网损成本变化如图 13 所 示 。 从 图 13 中 可 以 看 出 ，在 不 同 的 负 荷 水 平 下，本文所提出的网损优化模型都能够降低系统网 损成本，并且在负荷水平较高的条件下，网损最小和 网损成本最优 2 个优化目标下系统的网损成本相差 最多。 5.5 4.5 3.5 W M ／ 荷 负 2.5 0 6 12 时段 18 24 基准情景， 最大负荷日， 最小负荷日 图 12 不同负荷水平下的系统负荷 Ｆｉｇ．12 System load for different load levels 800 700 600 D U A ／ 本 成 损 网 500 0 6 12 祝 18 24 原始负荷水平网损最小 原始负荷水平网损成本最小 高负荷水平网损最小 高负荷水平网损成本最小 低负荷水平网损最小 低负荷水平网损成本最小 图 13 不同优化目标不同负荷水平下系统网损成本 Ｆｉｇ．13 System power鄄loss cost for different optimization objectives and different load levels 假设系统运行在不同负荷水平下，储能（充放电 策 略 ）和 DR（调 用 量 和 调 用 时 间 ）仍 采 用 原 始 负 荷 下的调用策略，在 祝 =12 的条件下，高负荷水平下的 系统网损成本为 693.45 AUD，低负荷水平下系统网 损成本为 643.73 AUD，仍小于网损最小运行策略下 0 6 12 祝 18 24 （b） 系统网损 DR 和储能网损成本最小 DR 和储能网损最小， 情景 1 图 11 不同优化目标下的系统网损和网损成本 Ｆｉｇ．11 System power鄄loss and power鄄loss cost for different optimization objectives 了 1.6 %。 在以网损成本最小的配电网运行策略下， 储能和 DR 的联合调控对于网损运行成本的降低效 果 也 最 明 显 ，在 不 同 的 祝 值 下 ，较 情 景 1 系 统 网 损 成本下降了 9.28 % ~ 12 %。 4 讨论 a. 模型鲁棒性检验。 为了检验上述模型的鲁棒性，本文选取情景 4 中 的配电网运行策略进行鲁棒性检验，利用蒙特卡洛抽 样，在电价波动约束下，选取了 15000 个电价样本，选 取 祝=12 时的系统运行策略进行验证，将电价样本代 入后，系统网损成本的样本均值为 619.541 AUD，最大 样本值为 648.376 AUD，最小样本值为 589.736 AUD， 没有超过 祝 = 12 时上述模型优化出的系统运行成本 651.607 AUD，因此，在相应的电价波动范围内，上述 模型的求解结果能够保证系统运行成本不增加。 集合算例中 4 种情景中的分析结果可以看出 ， 在网损最小的优化策略下，无论是储能还是 DR 参与 配电网运行调控后，都能够降低系统网损 。 在电力 市场环境下，以网损成本最小对配电网运行策略进行 优化时，储能和 DR 资源的接入也能够有效降低系统 整体的网损成本。 同时，在不同位置接入储能以及调 用不同负荷节点的 DR 都能够影响配电网的运行优 化策略 ，进而影响系统网损和整体的网损成 本 。 通 过对 2 个优化目标下的配电网运行策略的对比分析 可以得出，网损最小的配电网调控策略不一定适用 于电力市场环境下的 DNO，主要是因为一方面电价 的波动使得一天中各个时段的电价是不相同的 ；另 一方面，在考虑储能和 DR 资源约束后，当前时段的
    第 9 期 张旭东，等：考虑电价不确定性的主动配电网网损成本鲁棒优化模型 系统的网损成本 717.53 AUD、651.42 AUD。 5 结论 本文构建了考虑电价不确定性的 ADN 网 损 成 本优化模型，在考虑电价不确定性的条件下，通过对 比以网损最小和以网损成本最小为目标的配电网运 行策略，对储能、DR 接入后对 ADN 运行策略和网损 成本的影响进行了分析，从而为未来 DNO 对配电网 的运行管理提供一定的决策参考。 本文主要得出了 以下结论。 a． 在电力市场环境 下 ，储 能 和 DR 的 接 入 能 够 给未来 DNO 提供应对电价波动的调节工具，降低系 统的网损成本。 b． 在储能容量和 DR 参与程度相同的条件 下 ， 其接入位置的不同对系统网损和网损成本都能够产 生一定的影响。 并且 ，在考虑电价波动因 素 的 条 件 下，传统以网损最小的配电网运行优化策略不一定 适用于未来作为独立市场主体的 DNO，其造成的网 损成本往往要高于网损最小优化目标下的优化结果。 c． 在电力市场环境下 ，DR 是未来 ADN 中的重 要 可 调 控 资 源 ，协 调 优 化 系 统 中 “硬 储 能 ”（传 统 储 能）和“软储能”（DR 资源）能够更有效地降低配电网 网损成本。 参考文献： ［1］ 尤毅，刘东，于文鹏，等． 主动配电网技术及其进展［J］． 电力系统 自动化，2012，36（18）：10鄄16． YOU Yi，LIU Dong，YU Wenpeng，et al． Technology and its ZENG Ming． Some thoughts about deepening the reform of electrical industries of China［J］． China Power Enterprise Mana鄄 gement，2014，23（12）：62鄄64． ［7］ KARIM L A，MICHAEL G P． The role of distribution network operators in promoting cost鄄effective distributed generation：lessons from the united states of America for Europe［J］． Renewable and Sustainable Energy Reviews，2015，51（11）：484鄄496． ［8］ 陈政，曾鸣，张翔，等． 放松管制环境下基于改进布谷鸟搜索算法 的 DGO 与 DNO 效益均衡模型［J］． 电力建设，2015，36（8）：7鄄14． CHEN Zheng，ZENG Ming，ZHANG Xiang，et al． Benefit equili鄄 brium model of DGO and DNO in deregulated environment based on ICSA［J］． Electric Power Construction，2015，36（8）：7鄄14． ［9］ VASILEIOS A E，PAVLOS S G，NIKOS D H． Optimal operation of smart distribution networks：a review of models，methods and future research［J］． Electric Power Systems Research，2016，140： 95鄄106. ［10］ 章美丹，宋晓喆，辛 焕 海 ，等． 计 及 网 损 的 配 电 网 电 池 储 能 站 优 化运行策略［J］． 电网技术，2013，37（8）：2123鄄2128． ZHANG Meidan，SONG Xiaozhe，XIN Huanhai，et al． Optimal operation strategy of battery energy storage system in distribu鄄 tion networks with consideration of power losses［J］． Power System Technology，2013，37（8）：2123鄄2128． ［11］ HU Weihao，CHEN Zhe，BAK鄄JENSEN B，et al． Fuzzy adaptive particle swarm optimization for power loss minimization in distribution systems using optimal load response［J］． IET Gene鄄 ration，Transmission & Distribution，2014，8（1）：1鄄10． ［12］ DERAKHSHAN G，SHAYANFAR H A，KAZEMI A． The optimi鄄 zation of demand response programs in smart grids［J］． Energy Policy，2016，94（6）：295鄄306． ［13］ SHARMA I，BHATTACHARYA K，CA N軒 IZARES C． Smart dis鄄 tribution system operations with price鄄responsive and contro鄄 llable loads［J］． IEEE Transactions on Smart Grid，2015，6（2）： trends of active distribution network ［J］． Automation of Electric 795鄄807． Power Systems，2012，36（18）：10鄄16． ［2］ 李勋，龚庆武，胡元潮，等． 智能配电网体系探讨［J］． 电力自动化 设备，2011，31（8）：108鄄111． ［14］ ZHOU Lin，LI Furong，GU Chenghong，et al． Cost ／ benefit assess鄄 ment of a smart distribution system with intelligent electric vehicle charging ［J］． IEEE Transactions on Smart Grid，2014，5 LI Xun，GONG Qingwu，HU Yuanchao，et al． Discussion of smart （2）：839鄄847． distribution grid system ［J ］． Electric Power Automation Equip鄄 ［15］ GHASEMI S，MOSHTAGH J. A novel codification and modified ment，2011，31（8）：108鄄111． ［3］ 赵波，王财胜，周金辉，等． 主动配电网现状与未来发展［J］． 电力 系统自动化，2014，38（18）：125鄄135． heuristic approaches for optimal reconfiguration of distribution networks considering losses cost and cost benefit from voltage profile improvement ［J］. Applied Soft Computing，2014，25：360鄄 ZHAO Bo，WANG Caisheng，ZHOU Jinhui，et al． Present and 368. future development trend of active distribution network［J］． Auto鄄 ［16］ MISHRA A，FARZINFAR M，BAHADORNEJAD M，et al. Eva鄄 mation of Electric Power Systems，2014，38（18）：125鄄135． luating the impact of different PV control strategies on dis鄄 ［4］ 李 鹏 ，窦 彭 冲 ，李 雨 薇 ，等． 微 电 网 技 术 在 主 动 配 电 网 中 的 应 用 tribution network operation ［C］∥Power Engineering Conference ［J］． 电力自动化设备，2015，35（4）：8鄄16． （AUPEC），2014 Australasian Universities. ［S.l.］：IEEE，2014：1鄄6. LI Peng，DOU Pengchong，LI Yuwei，et al． Application of micro鄄 ［17］ 张建华，曾博，张 玉 莹 ，等． 主 动 配 电 网 规 划 关 键 问 题 与 研 究 展 grid technology in active distribution network［J］． Electric Power 望［J］． 电工技术学报，2014，29（2）：13鄄23． Automation Equipment，2015，35（4）：8鄄16． ZHANG Jianhua，ZENG Bo，ZHANG Yuying，et al． Key issues ［5］ 刘东，陈云辉，黄玉辉，等． 主动配电网的分层能量管理与协调控 and research prospects of active distribution network planning 制［J］． 中国电机工程学报，2014，34（31）：5500鄄5506． ［J］． Transactions of China Electrotechnical Society，2014，29 LIU Dong，CHEN Yunhui，HUANG Yuhui，et al． Hierarchical （2）：13鄄23． energy management and coordination control of active distribution ［18］ JABR R． Polyhedral formulations and loop elimination cons鄄 network［J］． Proceedings of the CSEE，2014，34（31）：5500鄄5506． traints for distribution network expansion planning ［J］． IEEE ［6］ 曾鸣． 深化我国电力体制改革的若干思考［J］． 中国电力企业管理， Transactions on Power Systems，2013，28（2）：1888鄄1897． 2014，23（12）：62鄄64． ［19］ 温俊强，曾博，张建华． 配电网中分布式风电可调鲁棒优化规划
    电 力 自 动 化 设 备 第 37 卷 ［J］． 电网技术，2016，40（1）：227鄄233． predicted error［J］． Proceedings of the CSEE，2004，24（12）：63鄄68． WEN Junqiang，ZENG Bo，ZHANG Jianhua． Adjustable robust optimization for distributed wind power planning in distribution 作者简介： network［J］． Power System Technology，2016，40（1）：227鄄233． ［20］ AMEO［EB ／ OL］． ［２０１６ 鄄 ０７ 鄄 ０１］. http：∥www.aemo.com.au ／ Elec鄄 tricity ／ Data ／ Price鄄and鄄Demand ／ Price鄄and鄄Demand鄄Graphs． ［21］ CONTRERAS J，ESPINOLA R，NOGALES F J，et al． ARIMA models to predict next鄄day electricity prices［J］． IEEE Transac鄄 tions on Power Systems，2003，18（3）：1014鄄1020． ［22］ 周 明 ，严 正 ，倪 以 信 ，等． 含 误 差 预 测 校 正 ARIMA 电 价 预 测 新 方法［J］． 中国电机工程学报，2004，24（12）：63鄄68． 张旭东 ZHOU Ming，YAN Zheng，NI Yixin，et al． A novel ARIMA 张 旭 东 （１９65 — ）， 男 ， 山 西 灵 丘 人 ， 博 士 研 究 生 ，主 要 研 究 方 向 为 电 力 技 术 经 济 、 电力市场（Ｅ鄄ｍａｉｌ：zxd鄄dl@163.com）； 王 昊 婧 （１９89 — ）， 女 ， 河 北 石 家 庄 人 ， 硕 士 ，主 要 研 究 方 向 为 电 力 技 术 经 济 、电 力 规划（Ｅ鄄ｍａｉｌ：wanghaojing2010@163.com）； 武 赓（１９9０ — ），男，河南南阳人 ，博士 研 究 生 ，主 要 研 究 方 向 为 需 求 响 应 、电 力 市 approach on electricity price forecasting with the improvement of 场（Ｅ鄄ｍａｉｌ：wugengmath@163.com）。 Robust power鄄loss cost optimization model considering price uncertainty for active distribution network ZHANG Xudong1，WANG Haojing2，WU Geng3，ZENG Ming3，ZHOU Xuan4 （1. School of Economics and Management，North China Electric Power University，Beijing 102206，China； 2. Beijing Electric Power Economic Research Institute，State Grid Beijing Electric Power Company， Beijing 100055，China；3. State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources，North China Electric Power University，Beijing 102206，China； 4. School of Electrical Engineering，Shanghai Dianji University，Shanghai 200245，China） Abstract： The main objective of system operation optimization of DNO （Distribution Network Operator） is to improve the operational efficiency and reliability of distribution network，but the fluctuation of electricity price in an open electricity market may affect the minimization of power鄄loss cost. A robust power鄄loss cost optimization model considering the price uncertainty is built for DNO. The impacts of price fluctuation， demand response and energy storage dispatch strategy on the power鄄loss cost are analyzed for different optimization objectives and the optimal operating strategy is given for different scenarios. The simulative results of IEEE 33鄄bus distribution network verify the effectiveness of the proposed model. Key words： active distribution network； DNO； power鄄loss cost； energy storage； demand response； robust optimization； models ）））））））））））））））））））））））））））））））））））））））））））））） （上接第 130 页 continued from page 130） Cost鄄benefit analysis and financing channels for demand response under electric reform SHEN Yunwei1，LI Ｙang1，JIAO Ｘize2，ZHOU Lei3，WANG Ｚhe1，WANG Ｃhen1 （1. School of Electrical Engineering，Southeast University，Nanjing 210096，China； 2. State Grid Jiangsu Electric Power Maintenance Branch Company，Nanjing 211102，China； 3. State Grid Suzhou Power Supply Company，Suzhou 215004，China） Abstract： The DR（Demand Response） implementations at home and abroad are researched ，the cost and benefit of each DR participant are analyzed，a DR cost鄄benefit model is built，and rational DR financing channels are proposed. The proposed model is verified by a case，the typical DR鄄participated loads are selected for simulation and analysis，and the feasibility and effectiveness of the proposed DR financing channels are proved. Research shows that，the rational improvement of the benefit鄄cost ratio of power grid enterprise may control the peak鄄valley difference of power grid while bring direct economic and social benefits to each participant. Key words： demand response； transmission and distribution price； cost鄄benefit analysis； benefit鄄cost ratio； financing channel
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料